C - 滑动窗口 /【模板】单调队列
Description
有一个长为 n 的序列 a,以及一个大小为 k 的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。
例如:
The array is [1,3,−1,−3,5,3,6,7] and k=3。

Input
输入一共有两行,第一行有两个正整数 n,k。
第二行 n 个整数,表示序列 a
Output
输出共两行,第一行为每次窗口滑动的最小值
第二行为每次窗口滑动的最大值
Sample 1
| Inputcopy | Outputcopy |
|---|---|
8 3 1 3 -1 -3 5 3 6 7 | -1 -3 -3 -3 3 3 3 3 5 5 6 7 |
Hint
【数据范围】
对于50% 的数据,1≤n≤10^5;
对于100% 的数据,1≤k≤n≤10^6,ai∈[−231,231)。
#include<iostream>
using namespace std;
const int N = 1e6 + 10;
int a[N], maxq[N], minq[N];
int n, m;//h是队头,用于输出答案;t是队尾,用于加入和删除元素
//注意:对头为左,队尾为右,队头只出,队尾可出可进;因此若队内有元素,则h<=t
//max队内的元素因保持单调递减的性质,加入的不是元素值,而是元素所在数组a中的下标
void maxfind() {int h = 0, t = -1;for (int i = 1; i <= n; i++){if (h <= t && maxq[h] <= i - m) h++; //不在当前滑动窗口的元素删除while (h <= t && a[i] >= a[maxq[t]]) t--; //a[i]为当前元素,若当前元素大于队尾的元素,则需要删除,时其满足单调递减的性质maxq[++t] = i; //加入新元素的下标if(i>=m) cout << a[maxq[h]] << " ";//输出结果}
}
//原理同上
void minfind() {int h = 0, t = -1;for (int i = 1; i <= n; i++){if (h <= t && minq[h] <= i - m) h++;while (h <= t && a[i] <= a[minq[t]]) t--;minq[++t] = i;if(i>=m) cout << a[minq[h]] << " ";}
}int main()
{cin >> n >> m;for (int i = 1; i <= n; i++) cin >> a[i];minfind();cout << endl;maxfind();return 0;
}单调队列模板(滑动窗口)_滑动窗口 /【模板】单调队列_胡牧之.的博客-CSDN博客
相关文章:

C - 滑动窗口 /【模板】单调队列
Description 有一个长为 n 的序列 a,以及一个大小为 k 的窗口。现在这个从左边开始向右滑动,每次滑动一个单位,求出每次滑动后窗口中的最大值和最小值。 例如: The array is [1,3,−1,−3,5,3,6,7] and k3。 Input 输入一共有…...

工厂人员作业行为动作识别检测算法
工厂人员作业行为动作识别检测算法通过yolov7python深度学习算法框架模型,工厂人员作业行为动作识别检测算法实时识别并分析现场人员操作动作行为是否符合SOP安全规范流程作业标准,如果不符合则立即抓拍告警提醒。Python是一种由Guido van Rossum开发的通…...
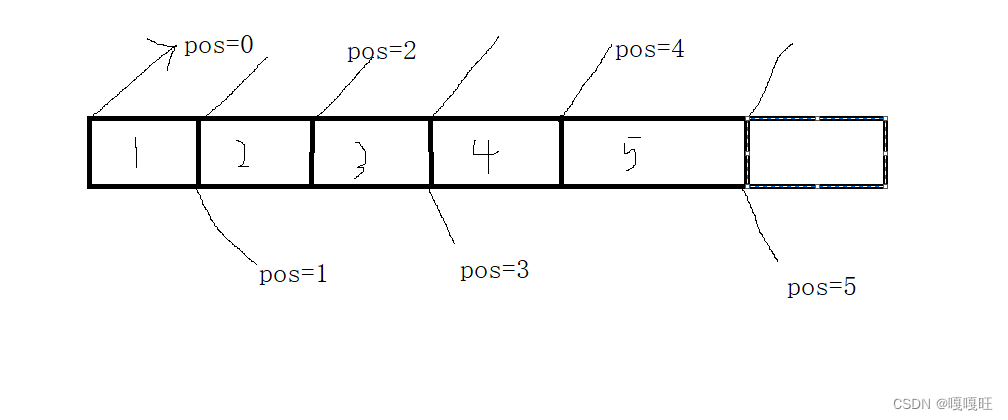
【数据结构】顺序表详解
当我们写完通讯录后,顺序表肯定难不倒你,跟着小张一起来学习顺序表吧! 线性表 线性表(linear list)是n个具有相同特性的数据元素的有限序列。 线性表是一种在实际中广泛使用的数据结构,常见的线性表&#x…...

HTML 播放器效果
效果图 实现代码 <!DOCTYPE HTML> <html><head><title>爱看动漫社区 | 首页 </title><link href"css/bootstrap.css" relstylesheet typetext/css /><!-- jQuery --><script src"js/jquery-1.11.0.min.js"…...
------装饰模式)
C++常用23种设计模式总结(三)------装饰模式
往期回顾 C常用23种设计模式总结(一)------单例模式 C常用23种设计模式总结(二)------观察者模式 什么是装饰模式 装饰模式是一种结构型设计模式,它允许你在运行时为对象动态添加新的行为。该模式通过将对象放入包装器中来实现这一点,这个包装器会实现与…...

选择O型圈时要考虑哪些因素?
为您的应用选择正确的O型圈对于确保适当的密封和较佳性能至关重要。O型圈可用的材料和尺寸多种多样,做出正确的选择可能需要知道一些重要的知识点。在本文中,我们将讨论选择O型圈时需要考虑的一些关键因素。 1、材料兼容性:先要考虑的因素是…...

安全管理中心技术测评要求项
1.系统管理-通过系统管理员进行系统管理操作 1-0/2-2/3-2/4-2 a)对系统管理员进行身份鉴别,只允许其通过特定的命令或操作界面进行系统管理操作,并对这些操作进行审计 b)通过系统管理员对系统的资源和运行进行配置、控制和管理&am…...
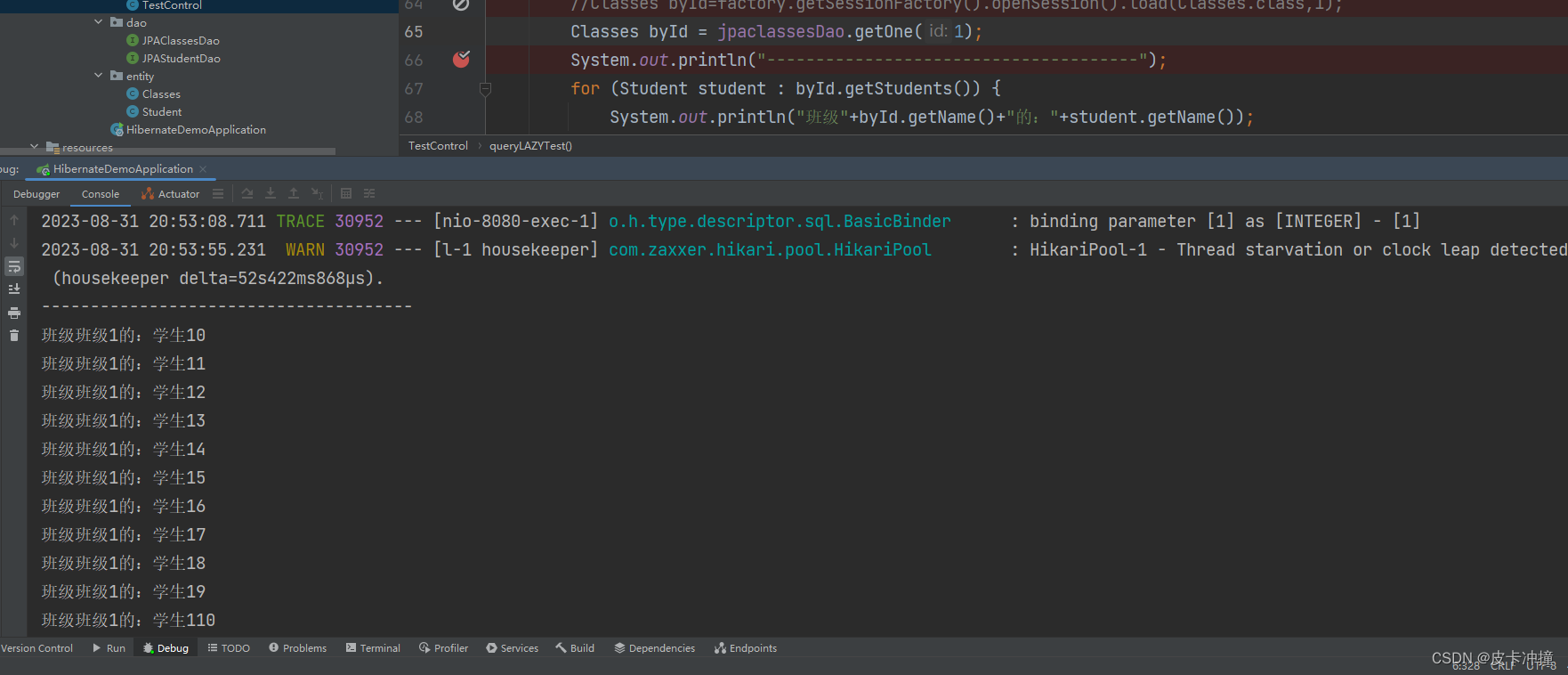
Hibernate(Spring Data)抓取策略
文章目录 示例代码放到最后,使用的是Springboot 项目1. 简介2. Hibernate抓取策略分类2.1 即时加载(Eager Loading)2.2 延迟加载(Lazy Loading)2.3 子查询加载(Subselect Loading)2.4 基于批处理…...
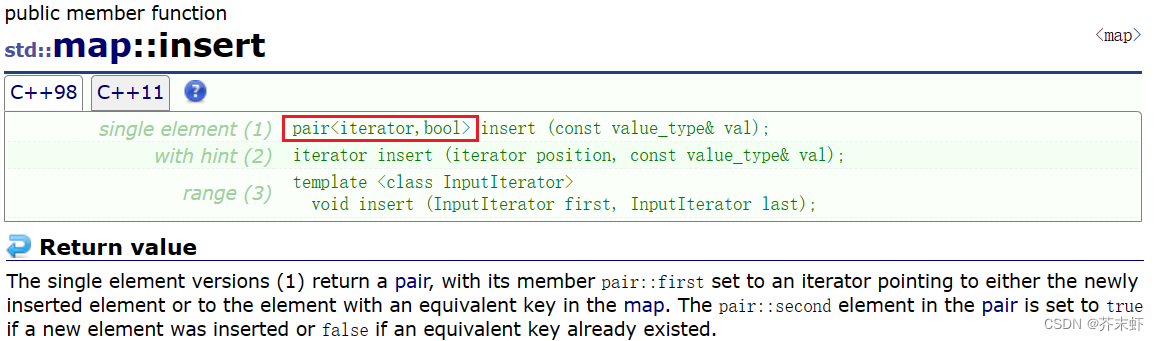
【高阶数据结构】map和set的介绍和使用 {关联式容器;键值对;map和set;multimap和multiset;OJ练习}
map和set的介绍和使用 一、关联式容器 关联式容器和序列式容器是C STL中的两种不同类型的容器。 关联式容器是基于键值对的容器,其中每个元素都有一个唯一的键值,可以通过键值来访问元素。关联式容器包括set、multiset、map和multimap。 序列式容器是…...

系统架构技能之设计模式-单件模式
一、开篇 其实我本来不是打算把系统架构中的一些设计模式单独抽出来讲解的,因为很多的好朋友也比较关注这方面的内容,所以我想通过我理解及平时项目中应用到的一 些常见的设计模式,拿出来给大家做个简单讲解,我这里只是抛砖引玉,…...
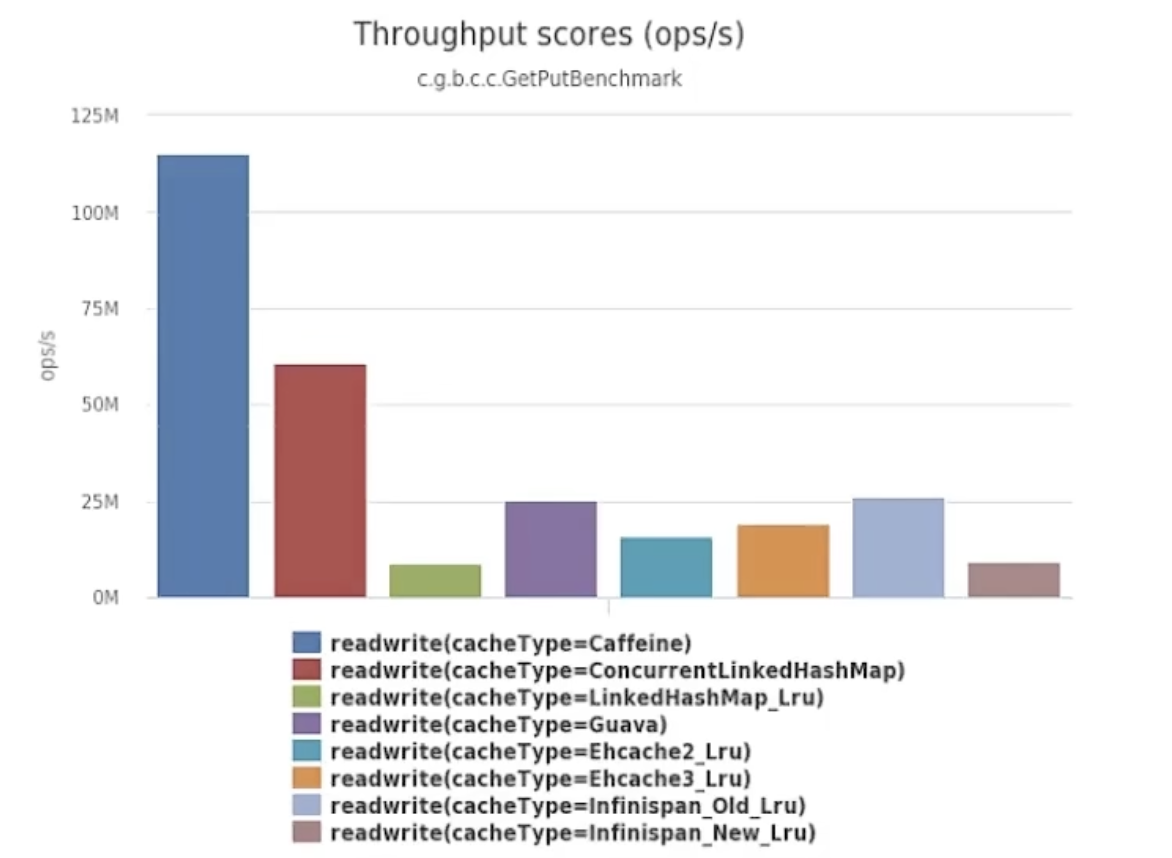
Redis进阶 - JVM进程缓存
原文首更地址,阅读效果更佳! Redis进阶 - JVM进程缓存 | CoderMast编程桅杆https://www.codermast.com/database/redis/redis-advance-jvm-process-cache.html 传统缓存的问题 传统的缓存策略一般是请求到达 Tomcat 后,先查询 Redis &…...

SD-WAN带您告别高成本、单一功能和安全性差
现今,随着企业规模不断扩大和分散办公越来越普遍,企业对于网络的需求也变得越来越高。然而,传统的组网方式面临着很多的问题,比如:成本高、功能单一、安全性差等问题。 传统组网方式有哪些? 传统的组网方式…...

面试必备:揭秘ArrayList和LinkedList,区别、优缺点与使用场景
大家好,我是你们的小米!今天我要跟大家聊一个在面试中经常被问到的热门话题——ArrayList和LinkedList的区别、优缺点以及它们的使用场景。作为程序员,掌握这些知识点不仅可以在面试中脱颖而出,还能帮助我们更好地在项目中选择合适…...
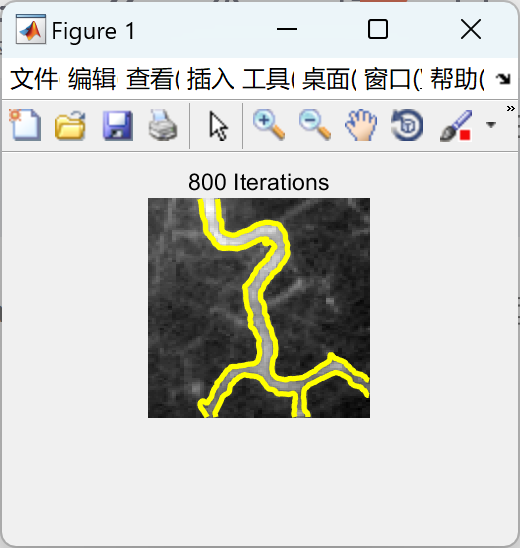
【局部活动轮廓】使用水平集方法实现局部活动轮廓方法研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

Git 同步远程新的同名分支
背景 因为远程分支的提交记录过多,导致本地的commit内容过大,会产生一些问题: 第一次拉取时间较长占用本地和远程的存储 原因 因为项目已有一些年头,若是每次文件提交比较大,那么占用空间就更大 解决方案 该方案…...

PingCode DevOps 团队:企业CICD流水线可能会遇到的问题及解法
CICD 流水线是指一系列自动化的构建、测试和部署步骤,用于将应用程序从开发到生产环境的过程。在 CICD 流水线中,每个步骤都是自动化的,并且在完成后会触发下一个步骤的执行。 CICD 的价值 CICD 流水线可以帮助团队更快地交付产品ÿ…...
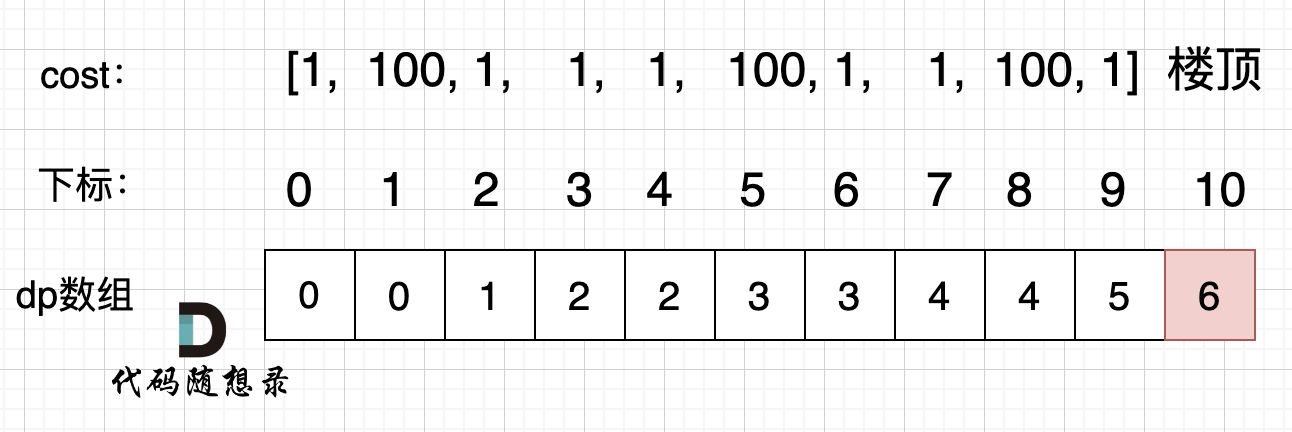
【LeetCode题目详解】第九章 动态规划part01 509. 斐波那契数 70. 爬楼梯 746. 使用最小花费爬楼梯 (day38补)
本文章代码以c为例! 一、力扣第509题:斐波那契数 题目: 斐波那契数 (通常用 F(n) 表示)形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是:…...
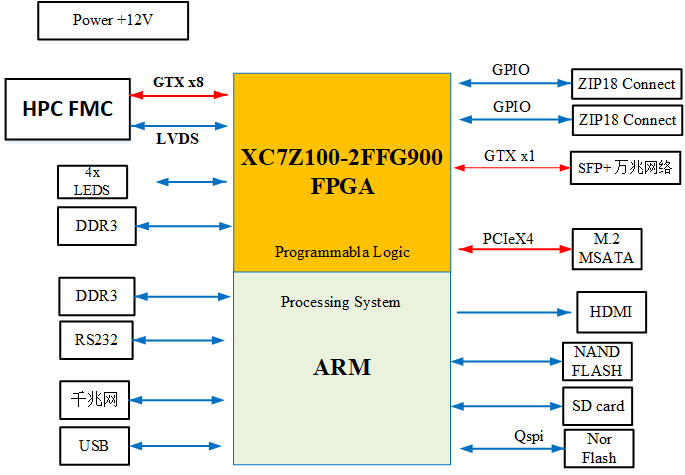
图像处理 信号处理板 设计原理图:367-基于zynq XC7Z100 FMC接口通用计算平台
基于zynq XC7Z100 FMC接口通用计算平台 一、板卡概述 板卡由SoC XC7Z100-2FFG900I芯片来完成卡主控及数字信号处理,XC7Z100内部集成了两个ARM Cortex-A9核和一个kintex 7的FPGA,通过PL端FPGA扩展FMC、光纤、IO等接口,PS端ARM扩展网络、USB、R…...
的七种用法)
PHP中header()的七种用法
我们在实际开发中经常使用header()实现一些功能,这篇文章介绍关于header()的7中用法,需要的伙伴的开参考一下。 PHP header()的7中用法: 1、跳转页面 可以使用header()实现跳转页面功能。 header(Location:.$url); // $url 跳转页面的地址…...

臻图信息以数字孪生技术推动智慧小区数字化建设
伴随着智慧城市建设进程的加速发展,加速传统小区的管理与服务向智能化升级转型。运用智慧化的管理和服务,利用信息技术和物联网等技术手段,将传统的居住区域与智能设备相结合,实现楼宇、社区设施、服务管理的数字化、网络化、智能…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
