Leetcode.1401 圆和矩形是否有重叠
题目链接
Leetcode.1401 圆和矩形是否有重叠 Rating : 1709
题目描述
给你一个以 (radius, xCenter, yCenter)表示的圆和一个与坐标轴平行的矩形 (x1, y1, x2, y2),其中 (x1, y1)是矩形左下角的坐标,而 (x2, y2)是右上角的坐标。
如果圆和矩形有重叠的部分,请你返回 true,否则返回 false。
换句话说,请你检测是否 存在 点 (xi, yi),它既在圆上也在矩形上(两者都包括点落在边界上的情况)。
示例 1 :

输入:radius = 1, xCenter = 0, yCenter = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
输出:true
解释:圆和矩形存在公共点 (1,0) 。
示例 2 :
输入:radius = 1, xCenter = 1, yCenter = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
输出:false
示例 3 :

输入:radius = 1, xCenter = 0, yCenter = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
输出:true
提示:
- 1<=radius<=20001 <= radius <= 20001<=radius<=2000
- −104<=xCenter,yCenter<=104-10^4 <= xCenter, yCenter <= 10^4−104<=xCenter,yCenter<=104
- −104<=x1<x2<=104-10^4 <= x1 < x2 <= 10^4−104<=x1<x2<=104
- −104<=y1<y2<=104-10^4 <= y1 < y2 <= 10^4−104<=y1<y2<=104
分析:

(x0,y0)是矩形的中心点,将其作为坐标系的原点,便于处理。
c是矩形的中心 (x0,y0)到圆心(xCenter,yCenter)的向量。
a是矩形的中心 (x0,y0)到(x2,y2)的向量。
b就是我们要求的 矩形 到 圆的向量,b = { c[0] - a[0] , c[1] - a[1] }。
我们只需要判断 向量b的模长 是否小于等于 圆的半径radius即可(判断 矩形 是否和 圆 相交)。
还有一些特殊情况:
此时 c[0] - a[0] < 0,所以我们就可以把它看成 0,即b = { 0 , c[1] - a[1] },就变成我们实际上要求的向量 u。

此时 c[1] - a[1] < 0,所以我们就可以把它看成 0,即b = { c[0] - a[0] ,0 },就变成我们实际上要求的向量 u。
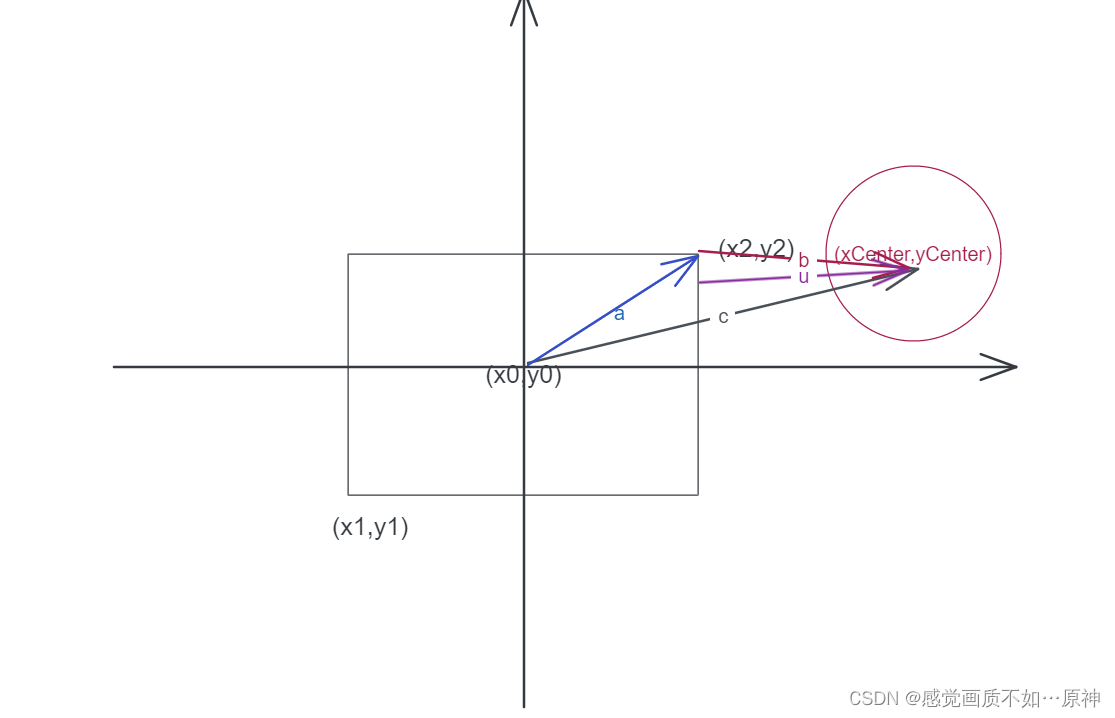
判断圆和矩形是否相交参考这个
时间复杂度 : O(1)O(1)O(1)
C++代码:
class Solution {
public:bool checkOverlap(int radius, int xCenter, int yCenter, int x1, int y1, int x2, int y2) {//求矩形中心点double x0 = (x1+x2)/2.0;double y0 = (y1+y2)/2.0;//求向量 c , a//用绝对值是为了让 x分量 和 y分量 都为正数,相当于将其映射到了第一象限(因为第一象限的坐标值都是正数)vector<double> c {abs(xCenter - x0),abs(yCenter - y0)};vector<double> a {x2 - x0,y2 - y0};//求向量 b 如果其中一个分量是负数的话,直接看作0vector<double> b {max(c[0] - a[0],0.0),max(c[1] - a[1],0.0)};return b[0] * b[0] + b[1] * b[1] <= radius * radius;}
};
Java代码:
class Solution {public boolean checkOverlap(int radius, int xCenter, int yCenter, int x1, int y1, int x2, int y2) {double x0 = (x1+x2)/2.0;double y0 = (y1+y2)/2.0;double[] c = new double[2];double[] a = new double[2];double[] b = new double[2];c[0] = Math.abs(xCenter - x0);c[1] = Math.abs(yCenter - y0);a[0] = x2 - x0;a[1] = y2 - y0;b[0] = Math.max(c[0] - a[0],0.0);b[1] = Math.max(c[1] - a[1],0.0);return b[0]*b[0] + b[1]*b[1] <= radius*radius;}
}
相关文章:

Leetcode.1401 圆和矩形是否有重叠
题目链接 Leetcode.1401 圆和矩形是否有重叠 Rating : 1709 题目描述 给你一个以 (radius, xCenter, yCenter)表示的圆和一个与坐标轴平行的矩形 (x1, y1, x2, y2),其中 (x1, y1)是矩形左下角的坐标,而 (x2, y2)是右上角的坐标。 如果圆和矩…...
CHAPTER 3 Web Server - httpd配置(二)
Web Server - httpd配置二3.1 httpd配置3.1.1 基于用户的访问控制3.1.2 basic认证配置示例:1. 添加用户2. 添加网页文件3. 定义安全域4. 修改父目录权限5. 访问效果6. 在配置文件中定义一个".htaccess"隐藏文件7. 添加组3.1.3 虚拟主机1. 构建方案2. 基于…...
VSCode 连接 SSH 服务器
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://blog.csdn.net/caroline_wendy/article/details/129133964 配置VSCode 下载VSCode:https://code.visualstudio.com/ 安装 Remote - SSH: 点击右下角蓝色图标: 连接服务器: 即可。 默认连接:ssh chen…...

如何选择靠谱的插画培训课程
如何选择靠谱的插画培训课程,今天教你3个维度选择一个靠谱的插画培训班! 插画培训机构课程: 1.选择插画培训班时,要先考察课程,看看课程内容是否符合自己的需求,是否有助于提高插画技术。课程设置应该灵活…...
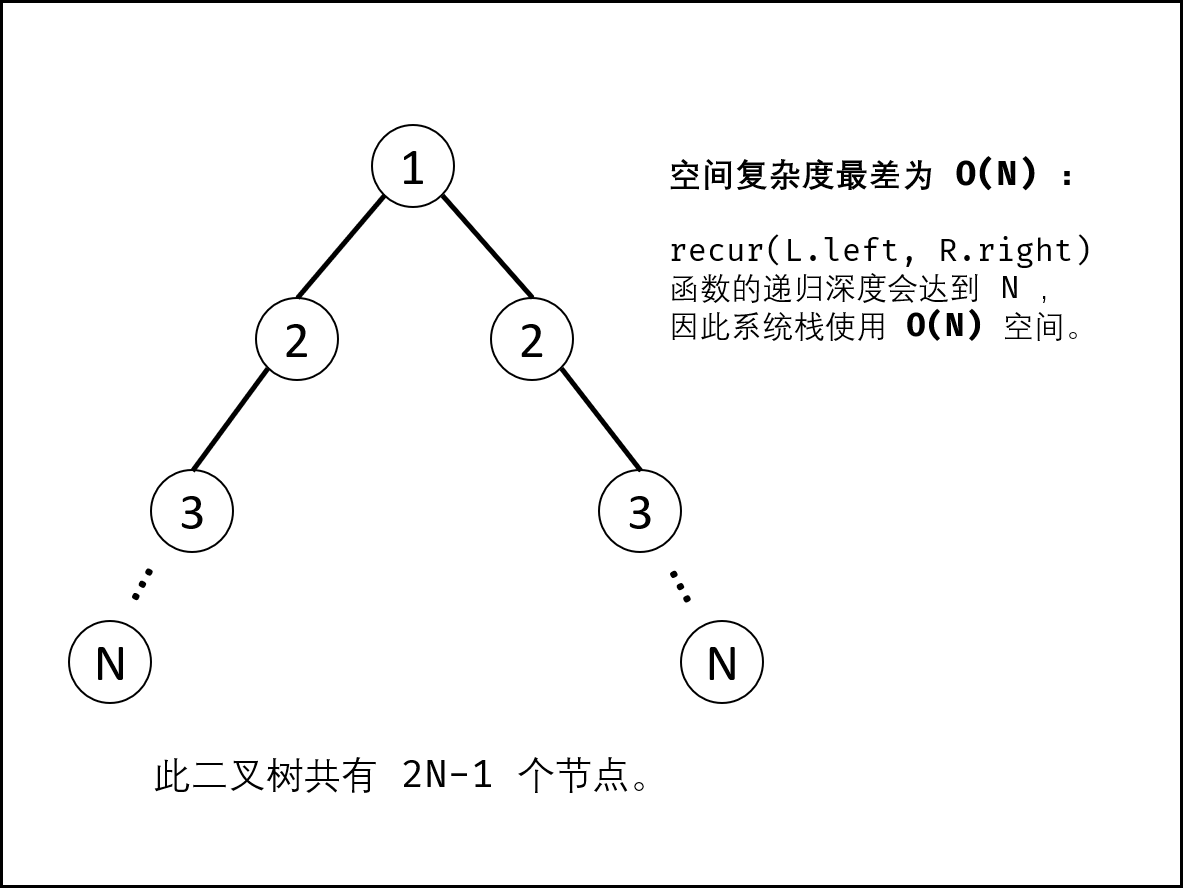
剑指 Offer 28. 对称的二叉树
剑指 Offer 28. 对称的二叉树 难度:easy\color{Green}{easy}easy 题目描述 请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。 例如,二叉树 [1,2,2,3,4,4,3] 是对称的。 但是下…...
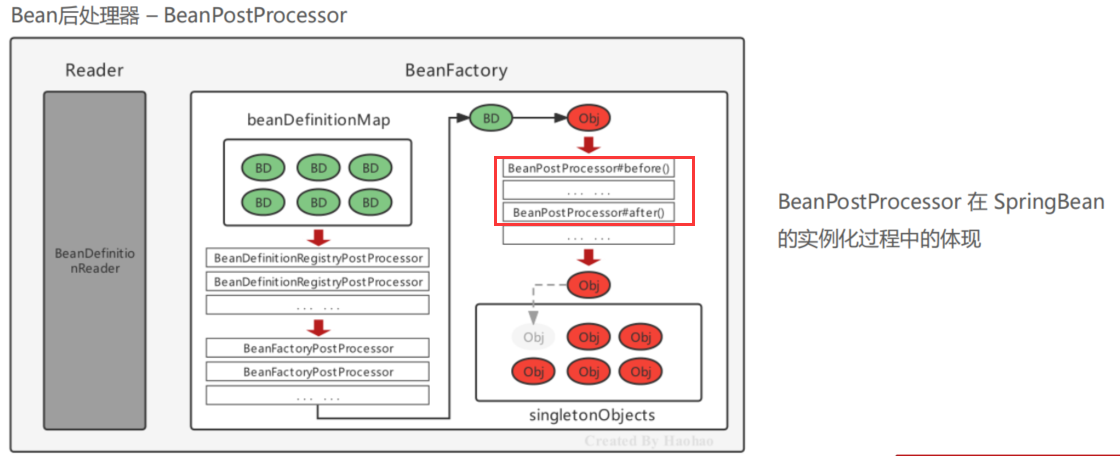
深入Spring底层透析后置处理器之豁然开朗篇
目录前言Spring的后置处理器Bean工厂后置处理器Bean后置处理器自定义Component实现注解开发前言 看这篇文章之前,需要了解Bean创建的过程,本篇文章是接着bean创建的基本流程的续写 Bean创建的基本过程:http://t.csdn.cn/1lK2d Spring的后置处…...
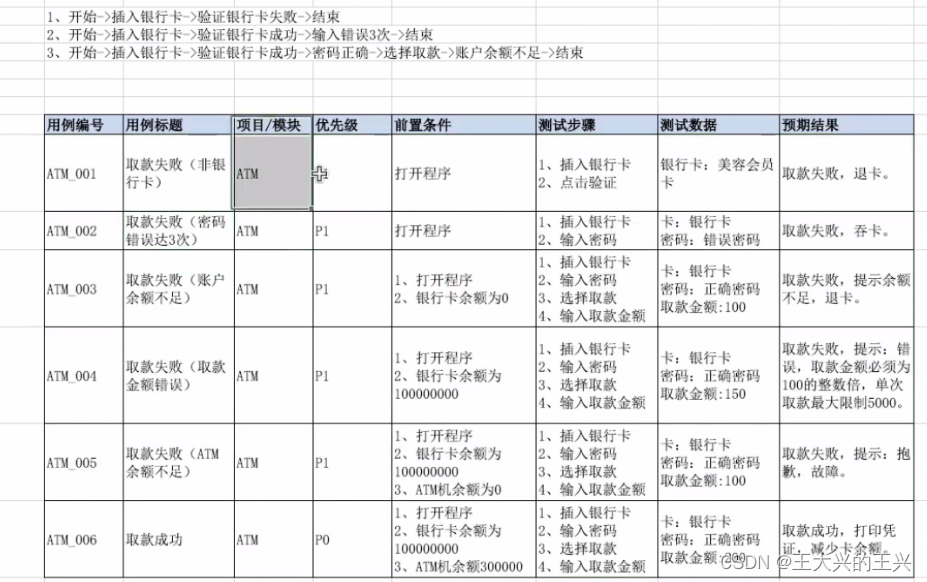
软件测试(基础定义篇)
测试基础 1、什么是软件测试?2、常见的测试分类3、质量模型 4、软件测试流程 5、测试用例 6、测试用例设计方法 )1、什么是软件测试? 1、什么是软件? 答:软件是控制计算机硬件工作的工具。 2、软件的组成? 3、什么是…...

华为OD机试 - 寻找目标字符串 | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 简易压缩算法(Python) | 机试题算法思路 【2023】 华为OD机试题 - 获取最大软件版本号(JavaScript) 华为OD机试 - 猜字谜(Python) | 机试题+算法思路 【2023】 华为OD机试 - 删除指定目录(Python) | 机试题算法思路 【2023】 华为OD机试 …...
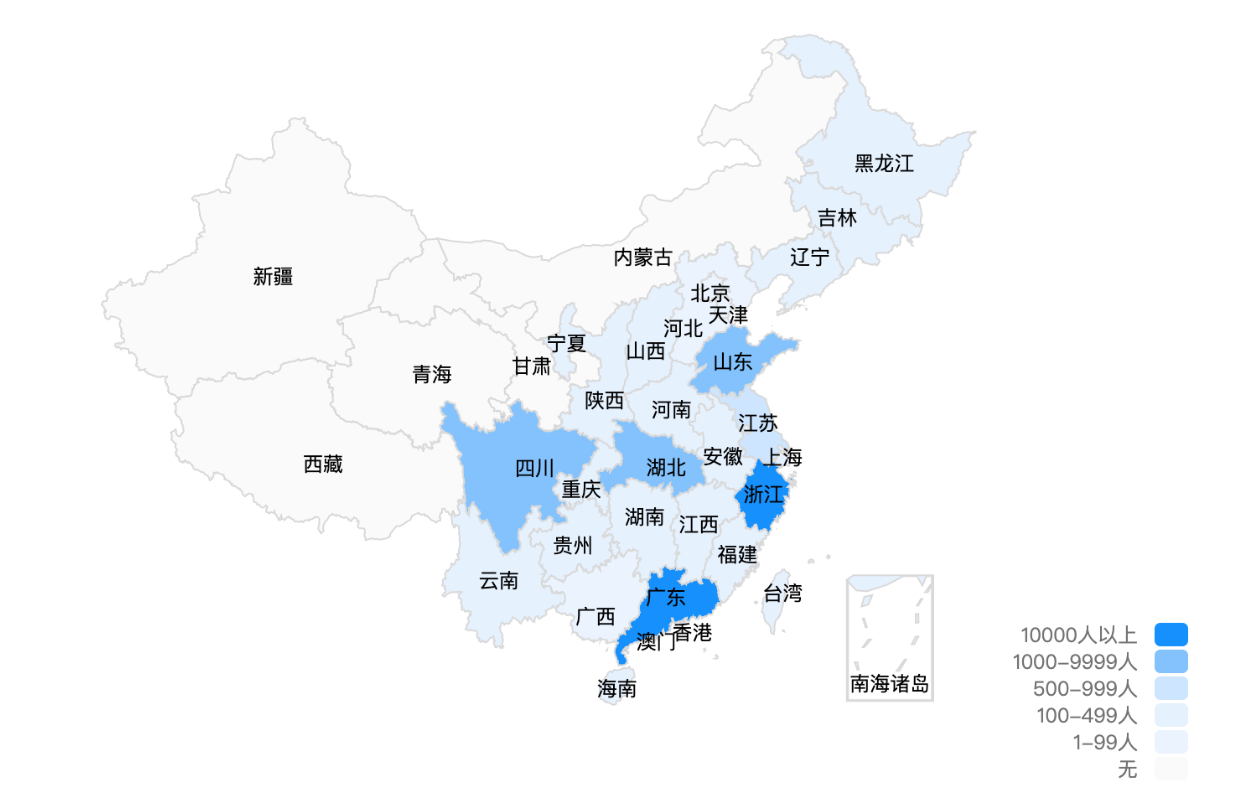
使用echart绘制中国地图并显示人数
文章目录引言效果如图所示vue中echarts4.9版本,地图的使用引言 在做毕设的过程中,有一个需求:根据用户的ip,在前端展示出中国地图,然后展现出每个省有多少人这样子 经过百度后,发现可以使用echart来完成该…...
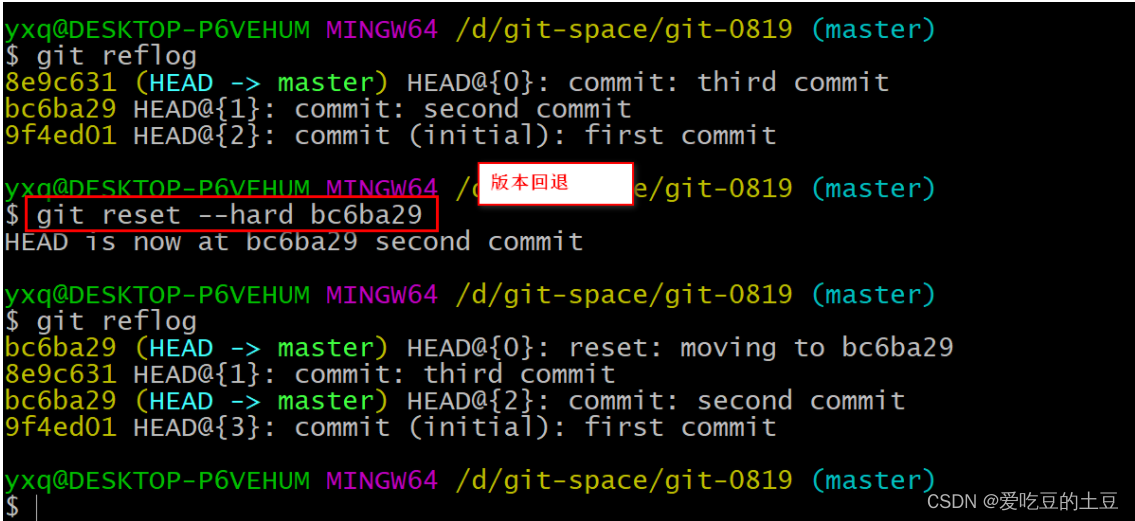
Git的常用命令
1:软件安装1.1:Git下载与安装百度上搜索Git官网:https://git-scm.com/下载:https://git-scm.com/download/win下载Git安装程序,双击安装 Git-2.9.3.2-64-bit.exe配置环境变量path 使用git --version查看 git 是否安装成…...

AcWing1018.最低通行费
1018.最低通行费一个商人穿过一个 NN 的正方形的网格,去参加一个非常重要的商务活动。他要从网格的左上角进,右下角出。每穿越中间 1 个小方格,都要花费 1 个单位时间。商人必须在 (2N−1)(2−1) 个单位时间穿越出去。而在经过中间的每个小方…...

【面试题】vue中的插槽是什么?
大厂面试题分享 面试题库后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库一、slot是什么在HTML中 slot 元素 ,作为 Web Components 技术套件的一部分,是Web组件内的一个占位符该占位符可以在后期…...

Go语言结构体struct详解,Go空结构体的这些妙用你知道吗?
本文详解了Go语言结构体的各个知识点,最后介绍了空结构体的3种妙用。希望对你有帮助。 定义 结构体,是一种自定义的数据类型,由多个数据类型组合而成。用于描述一类事物相关属性。 定义方式: type 类型名 struct {字段名 字段类…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 航天器(Python) | 机试题+算法思路+考点+代码解析 【2023】
航天器 题目 给航天器一侧加装长方形和正方形的太阳能板(图中的斜线区域); 需要先安装两个支柱(图中的黑色竖条); 再在支柱的中间部分固定太阳能板; 但航天器不同位置的支柱长度不同; 太阳能板的安装面积受限于最短一侧的那支支柱的长度; 现提供一组整型数组的支柱高度数据;…...

【Optional】告别丑陋判空,使用Optional类
一、概述 当项目中充斥着大量的、丑陋的判空语句,如下: if (user ! null) {Address address user.getAddress();if (address ! null) {Country country address.getCountry();if (country ! null) {String isocode country.getIsocode();if (isocod…...
魔兽世界服务端端新手搭建教程
明杰也是很久以前开始研究魔兽服务器架设,主要原因是亚服经常要排队6-7个小时,去不排除的服和单机没啥区别,以怀旧服玩到10级以后就开始玩335端,一开始也和新入手的人一样云里雾里的,经过长时间的学习总算有点成就,向新…...
宝塔搭建实战人才求职管理系统mobile手机端vue源码(五)
大家好啊,我是测评君,欢迎来到web测评。 上一期给大家分享骑士cms会员管理member前端vue在本地运行打包、宝塔发布部署的方式,本期给大家分享,mobile移动端vue怎么在本地运行,打包,实现线上功能更新替换的方…...

生态应用:探讨 NGINX 与上下游系统集成时的开发经验
NGINX 作为一款高性能的 Web 服务器和反向代理服务器,在各种应用场景中广泛应用。随着业务的发展,我们在使用 NGINX 时,可能需要将其与其他系统进行集成,以实现更加复杂的业务需求。 本文将结合实际应用场景,探讨 NGI…...
ArcGIS批量拼接大量栅格遥感影像:Mosaic工具
本文介绍在ArcGIS下属的ArcMap软件中,基于Mosaic工具,批量对大量栅格遥感影像文件加以拼接、镶嵌的方法。 在GIS应用中,我们时常需要对大量栅格遥感影像数据加以批量拼接的工作。这一步骤可以基于Python语言实现,具体可以参考文章…...

Flink UI部署jar包报错
错误描述: 通过Flink的UI中的Submit New Job菜单添加jar包的时候提示报错。报错信息的关键字是“The LocalStreamEnvironment cannot be used when submitting a program through a client, or running in a TestEnvironment context”,最关键的是“Loc…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

【Elasticsearch】Elasticsearch 在大数据生态圈的地位 实践经验
Elasticsearch 在大数据生态圈的地位 & 实践经验 1.Elasticsearch 的优势1.1 Elasticsearch 解决的核心问题1.1.1 传统方案的短板1.1.2 Elasticsearch 的解决方案 1.2 与大数据组件的对比优势1.3 关键优势技术支撑1.4 Elasticsearch 的竞品1.4.1 全文搜索领域1.4.2 日志分析…...
