用Python搓一个黑洞
文章目录
- 简介
- 单位制
- 观测绘图
简介
黑洞图像大家都知道,毕竟前几年刚发布的时候曾火遍全网,甚至都做成表情包了。

问题在于,凭什么认为这就是黑洞的照片,而不是一个甜甜圈啥的给整模糊了得到的呢?有什么理论依据吗?
单位制
利用einsteinpy模块中的Shadow类,可以实现黑洞吸积盘的发射强度,换言之,用理论模拟一下黑洞的照片应该是什么样子的。
22年5月份发布的是人马座A*的照片,这个"黑洞"的质量为8.26×10368.26\times10^{36}8.26×1036kg,距离地球26673光年。
根据源码推测,einstenipy中采用几何单位制,光速和万有引力常数设为1, 即c=G=1c=G=1c=G=1。现设几何单位制下的时间、距离以及质量单位为S,M,KGS, M, KGS,M,KG,国际制单位为s,m,kgs, m, kgs,m,kg,若以时间单位秒为基本单位,即1s=1S1s=1S1s=1S,由于几何单位制下光速c=1M/Sc=1M/Sc=1M/S,则可得到距离单位的换算关系
c=3×108m/sc=1M/S1s=1S→1M=3×108m\begin{aligned} c&=3\times 10^8 m/s\\ c&=1M/S\\ 1s&=1S \end{aligned}\to 1M=3\times10^8m cc1s=3×108m/s=1M/S=1S→1M=3×108m
同理,根据万有引力常数可得到质量单位的换算关系
G=6.67×10−11m3kg−1s−2G=1M3KG−1S−21S=1s1M=3×108m→1KG−1=0.24×10−35kg−11kg=0.24×10−35KG\begin{aligned} G&=6.67\times10^{-11}m^3kg^{-1}s^{-2}\\ G&=1M^3KG^{-1}S^{-2}\\ 1S&=1s\\ 1M&=3\times10^8m \end{aligned}\to \begin{aligned} 1KG^{-1}=0.24\times10^{-35}kg^{-1}\\ 1kg=0.24\times10^{-35}KG \end{aligned} GG1S1M=6.67×10−11m3kg−1s−2=1M3KG−1S−2=1s=3×108m→1KG−1=0.24×10−35kg−11kg=0.24×10−35KG
所以质量和距离可以分别表示为
8.26×1036kg=1.982KG26673lyr=2.52×1020m=8.4×13M8.26\times10^{36}kg=1.982KG\\ 26673\operatorname{lyr}=2.52\times10^{20}m=8.4\times^{13}M 8.26×1036kg=1.982KG26673lyr=2.52×1020m=8.4×13M
观测绘图
尽管我们在地球上观测这个黑洞,但由于相机镜头等因素,实际上肯定不能用这么大的尺度来观测,所以稍微选一个差不多的距离就好
import astropy.units as u
from einsteinpy.rays import Shadow
mass = 1.98 * u.kg
fov = 100 * u.km
shadow = Shadow(mass=mass, fov=fov, n_rays=1000)
shadow就是其发射模型,其内部用于绘图的主要成员有
fb1xxx负半轴fb2xxx正半轴intensity发射强度
下面绘制一下不同距离处的发射强度
import matplotlib.pyplot as plt
plt.plot(shadow.fb1, shadow.intensity, "r")
plt.plot(shadow.fb2, shadow.intensity, "r")
plt.xlabel("Impact Paramter (b)")
plt.ylabel("Intensity (Emissivity)")
plt.title("Intensity Plot")
plt.grid()
plt.show()
结果如下图所示,果然中间凹了下去

einsteinpy内嵌了绘图函数,通过ShadowPlotter(shadow, is_line_plot=True)可以更加方便地绘制上述图像,如果将is_line_plot设为False,则可得到强度分布图
from einsteinpy.plotting import ShadowPlotter
obj = ShadowPlotter(shadow=shadow, is_line_plot=False)
obj.plot()
obj.show()
plt.show()

这样一看是不是觉得和前面的那个甜甜圈确有相似之处。
这个模型是根据Cosimo Bambi的文章编写的,论文地址在这:Cosimo Bambi, 10.1103/PhysRevD.87.107501。本来合计着把这篇文章的公式啥的粘过来解读一下,但考虑到贴在这也没人看,想想还是算了。
相关文章:

用Python搓一个黑洞
文章目录简介单位制观测绘图简介 黑洞图像大家都知道,毕竟前几年刚发布的时候曾火遍全网,甚至都做成表情包了。 问题在于,凭什么认为这就是黑洞的照片,而不是一个甜甜圈啥的给整模糊了得到的呢?有什么理论依据吗&…...
Spring MVC常用功能及注解
目录 一、什么是Spring MVC 1.1 Spring MVC定义 1.2 MVC定义 1.3 MVC和Spring MVC的关系 1.4 Spring MVC的作用 二、Spring MVC的使用 2.1 Spring MVC的创建和连接 2.1.1 RequestMapping注解 2.1.2 GetMapping注解 2.1.3 PostMapping注解 2.2 获取参数 2.2.1 获取单…...

shell 编程
文章目录一、shell 编程1.1. 脚本执行1.2. 变量1.3. 特殊变量1.4. 运算符1.5. for 循环1.6. while 循环1.7. case 语句1.8. read 命令1.9. if 判断1.10. 判断语句1.11. 自定义函数1.12. 脚本调试二、sed2.1. sed 选项2.2. sed function2.3. sed 删除(d 命令…...
Leetcode.1401 圆和矩形是否有重叠
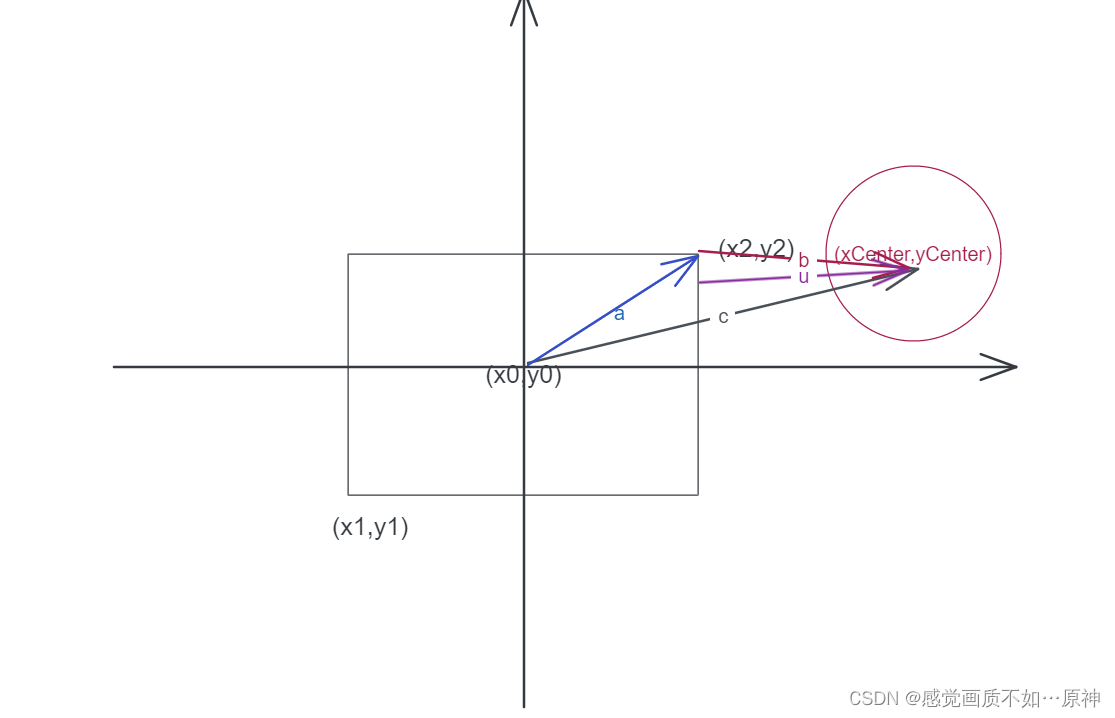
题目链接 Leetcode.1401 圆和矩形是否有重叠 Rating : 1709 题目描述 给你一个以 (radius, xCenter, yCenter)表示的圆和一个与坐标轴平行的矩形 (x1, y1, x2, y2),其中 (x1, y1)是矩形左下角的坐标,而 (x2, y2)是右上角的坐标。 如果圆和矩…...
CHAPTER 3 Web Server - httpd配置(二)
Web Server - httpd配置二3.1 httpd配置3.1.1 基于用户的访问控制3.1.2 basic认证配置示例:1. 添加用户2. 添加网页文件3. 定义安全域4. 修改父目录权限5. 访问效果6. 在配置文件中定义一个".htaccess"隐藏文件7. 添加组3.1.3 虚拟主机1. 构建方案2. 基于…...
VSCode 连接 SSH 服务器
欢迎关注我的CSDN:https://spike.blog.csdn.net/ 本文地址:https://blog.csdn.net/caroline_wendy/article/details/129133964 配置VSCode 下载VSCode:https://code.visualstudio.com/ 安装 Remote - SSH: 点击右下角蓝色图标: 连接服务器: 即可。 默认连接:ssh chen…...

如何选择靠谱的插画培训课程
如何选择靠谱的插画培训课程,今天教你3个维度选择一个靠谱的插画培训班! 插画培训机构课程: 1.选择插画培训班时,要先考察课程,看看课程内容是否符合自己的需求,是否有助于提高插画技术。课程设置应该灵活…...
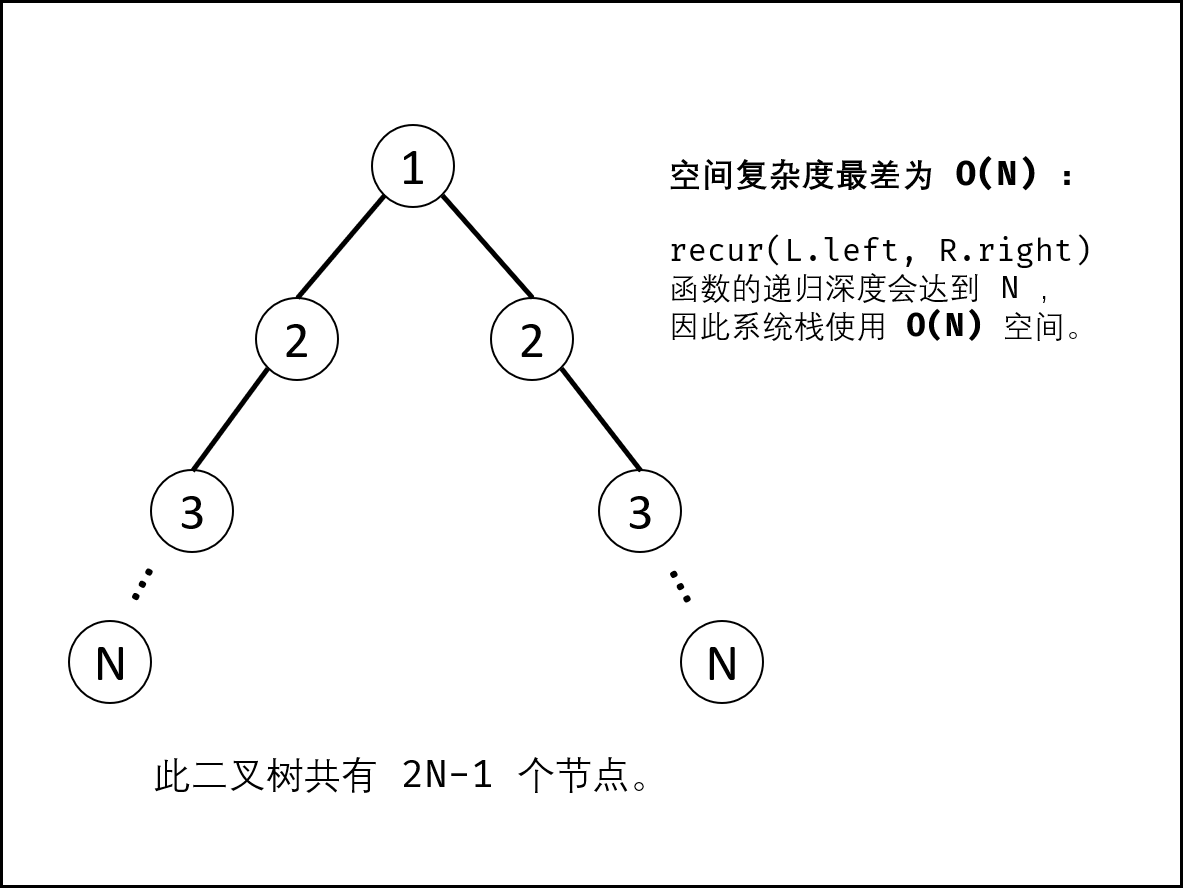
剑指 Offer 28. 对称的二叉树
剑指 Offer 28. 对称的二叉树 难度:easy\color{Green}{easy}easy 题目描述 请实现一个函数,用来判断一棵二叉树是不是对称的。如果一棵二叉树和它的镜像一样,那么它是对称的。 例如,二叉树 [1,2,2,3,4,4,3] 是对称的。 但是下…...
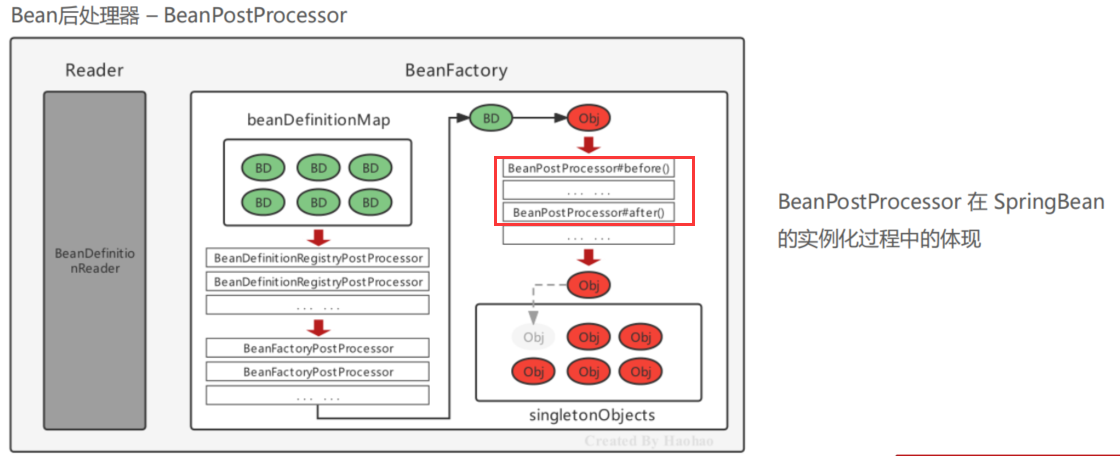
深入Spring底层透析后置处理器之豁然开朗篇
目录前言Spring的后置处理器Bean工厂后置处理器Bean后置处理器自定义Component实现注解开发前言 看这篇文章之前,需要了解Bean创建的过程,本篇文章是接着bean创建的基本流程的续写 Bean创建的基本过程:http://t.csdn.cn/1lK2d Spring的后置处…...
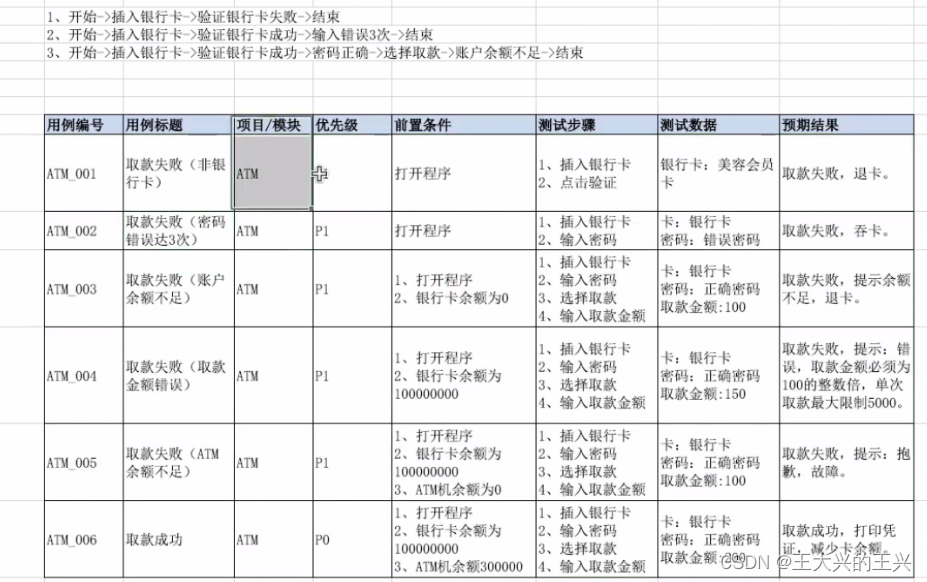
软件测试(基础定义篇)
测试基础 1、什么是软件测试?2、常见的测试分类3、质量模型 4、软件测试流程 5、测试用例 6、测试用例设计方法 )1、什么是软件测试? 1、什么是软件? 答:软件是控制计算机硬件工作的工具。 2、软件的组成? 3、什么是…...

华为OD机试 - 寻找目标字符串 | 机试题算法思路 【2023】
最近更新的博客 华为OD机试 - 简易压缩算法(Python) | 机试题算法思路 【2023】 华为OD机试题 - 获取最大软件版本号(JavaScript) 华为OD机试 - 猜字谜(Python) | 机试题+算法思路 【2023】 华为OD机试 - 删除指定目录(Python) | 机试题算法思路 【2023】 华为OD机试 …...
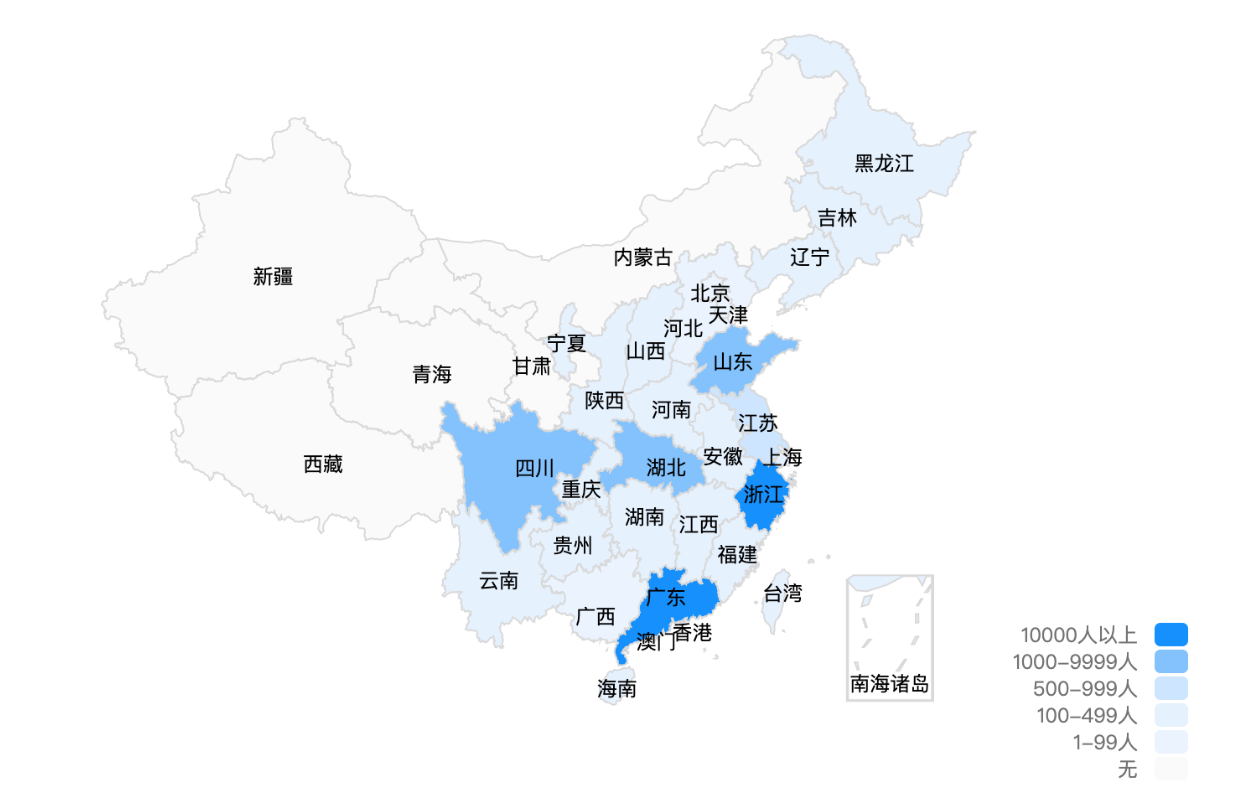
使用echart绘制中国地图并显示人数
文章目录引言效果如图所示vue中echarts4.9版本,地图的使用引言 在做毕设的过程中,有一个需求:根据用户的ip,在前端展示出中国地图,然后展现出每个省有多少人这样子 经过百度后,发现可以使用echart来完成该…...
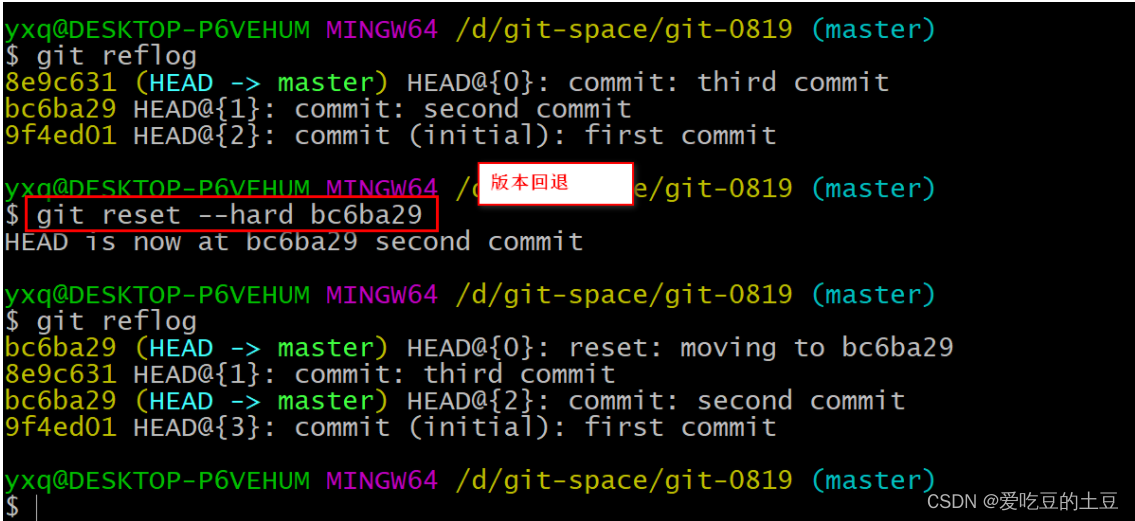
Git的常用命令
1:软件安装1.1:Git下载与安装百度上搜索Git官网:https://git-scm.com/下载:https://git-scm.com/download/win下载Git安装程序,双击安装 Git-2.9.3.2-64-bit.exe配置环境变量path 使用git --version查看 git 是否安装成…...

AcWing1018.最低通行费
1018.最低通行费一个商人穿过一个 NN 的正方形的网格,去参加一个非常重要的商务活动。他要从网格的左上角进,右下角出。每穿越中间 1 个小方格,都要花费 1 个单位时间。商人必须在 (2N−1)(2−1) 个单位时间穿越出去。而在经过中间的每个小方…...

【面试题】vue中的插槽是什么?
大厂面试题分享 面试题库后端面试题库 (面试必备) 推荐:★★★★★地址:前端面试题库一、slot是什么在HTML中 slot 元素 ,作为 Web Components 技术套件的一部分,是Web组件内的一个占位符该占位符可以在后期…...

Go语言结构体struct详解,Go空结构体的这些妙用你知道吗?
本文详解了Go语言结构体的各个知识点,最后介绍了空结构体的3种妙用。希望对你有帮助。 定义 结构体,是一种自定义的数据类型,由多个数据类型组合而成。用于描述一类事物相关属性。 定义方式: type 类型名 struct {字段名 字段类…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 航天器(Python) | 机试题+算法思路+考点+代码解析 【2023】
航天器 题目 给航天器一侧加装长方形和正方形的太阳能板(图中的斜线区域); 需要先安装两个支柱(图中的黑色竖条); 再在支柱的中间部分固定太阳能板; 但航天器不同位置的支柱长度不同; 太阳能板的安装面积受限于最短一侧的那支支柱的长度; 现提供一组整型数组的支柱高度数据;…...

【Optional】告别丑陋判空,使用Optional类
一、概述 当项目中充斥着大量的、丑陋的判空语句,如下: if (user ! null) {Address address user.getAddress();if (address ! null) {Country country address.getCountry();if (country ! null) {String isocode country.getIsocode();if (isocod…...
魔兽世界服务端端新手搭建教程
明杰也是很久以前开始研究魔兽服务器架设,主要原因是亚服经常要排队6-7个小时,去不排除的服和单机没啥区别,以怀旧服玩到10级以后就开始玩335端,一开始也和新入手的人一样云里雾里的,经过长时间的学习总算有点成就,向新…...
宝塔搭建实战人才求职管理系统mobile手机端vue源码(五)
大家好啊,我是测评君,欢迎来到web测评。 上一期给大家分享骑士cms会员管理member前端vue在本地运行打包、宝塔发布部署的方式,本期给大家分享,mobile移动端vue怎么在本地运行,打包,实现线上功能更新替换的方…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

初探Service服务发现机制
1.Service简介 Service是将运行在一组Pod上的应用程序发布为网络服务的抽象方法。 主要功能:服务发现和负载均衡。 Service类型的包括ClusterIP类型、NodePort类型、LoadBalancer类型、ExternalName类型 2.Endpoints简介 Endpoints是一种Kubernetes资源…...

人工智能--安全大模型训练计划:基于Fine-tuning + LLM Agent
安全大模型训练计划:基于Fine-tuning LLM Agent 1. 构建高质量安全数据集 目标:为安全大模型创建高质量、去偏、符合伦理的训练数据集,涵盖安全相关任务(如有害内容检测、隐私保护、道德推理等)。 1.1 数据收集 描…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

C++_哈希表
本篇文章是对C学习的哈希表部分的学习分享 相信一定会对你有所帮助~ 那咱们废话不多说,直接开始吧! 一、基础概念 1. 哈希核心思想: 哈希函数的作用:通过此函数建立一个Key与存储位置之间的映射关系。理想目标:实现…...

C# WPF 左右布局实现学习笔记(1)
开发流程视频: https://www.youtube.com/watch?vCkHyDYeImjY&ab_channelC%23DesignPro Git源码: GitHub - CSharpDesignPro/Page-Navigation-using-MVVM: WPF - Page Navigation using MVVM 1. 新建工程 新建WPF应用(.NET Framework) 2.…...
