【位运算】位运算常用技巧总结
目录
前言
一.常见的小问题
1.给定一个数n,确定它的二进制表示中的第x位是0还是1
2.给定一个数n,将它的二进制表示中的第x位修改成1
3.给定一个数n,将它的二进制表示中的第x位修改成0
4.给定一个数n,提取它的二进制表示中最右侧的1(即将其它位置位0)
5.给定一个数n,去掉它的二进制表示中最右侧的1
6.异或运算的规则
二.典型例题
前言
位运算是一类常考的题型,关于位运算的操作符有以下几种:
按位取反(~)
左移操作符(<<)
右移操作符(>>)
按位与(&)
按位或 (|)
按位异或(^)
重点要区分&,|和^这几个操作符,按位与是有0则0,按位或是有1则1
按位异或相同为0,相异为1。也可以记成“无进位相加”,例如1+1=2, 因为是二进制所以变成0,但是不进位。
接下来介绍怎么利用这些操作符来解决常见的问题
一.常见的小问题
1.给定一个数n,确定它的二进制表示中的第x位是0还是1
首先声明,默认最低位是第0位。
方法:将n右移x位,与1做按位与操作,若结果为1,则n的第x位是1,若结果是0,则第x位是0
说明:右移操作是为了将第x位移到最低位,方便与1的最低位按位与,而1的其它位全是0,有0则0,故其它位的结果肯定是0,而最低位的结果则取决于x位是0还是1
代码操作:(n >> x) & 1
2.给定一个数n,将它的二进制表示中的第x位修改成1
方法:将1左移x位,再与n按位或
说明:将1左移x位是为了对n的第x位进行“定向打击”,1的第x位是1,其余位是0。按位或的特点是有1则1,故结果的第x位肯定是1,其它位取决于n的其它位是0还是1,和原来相比不会变化
代码操作:n = (1 << x) | n
3.给定一个数n,将它的二进制表示中的第x位修改成0
方法:将1左移x位,按位取反,再与n按位与
说明:按位与的特点是有0则0,故结果的第x位肯定是0,其它位取决于n的其它位是0还是1,和原来相比不会发生变化
代码操作:n = (~(1 >> x) ) & n
4.给定一个数n,提取它的二进制表示中最右侧的1(即将其它位置位0)
方法:n & -n
说明:由n向-n转变,先将n按位取反,然后加1,这样使得n最右侧的1,左边区域全变成相反,右边区域全变成0,而按位与的特点是有0则0,故只有最右侧的1异或的结果是1,其余全是0。

5.给定一个数n,去掉它的二进制表示中最右侧的1
方法:n & (n - 1)
说明:由n到n-1,最右侧1的左边区域不变,右边区域(包括1)全部变成相反,按位与的特点是有0则0,故最右侧的1肯定会变成0,其余位不变

6.异或运算的规则
a ^ 0 = a
a ^ a = 0
a ^ b ^ c = a ^ c ^ b
二.典型例题
接下来有几道例题,大家可以先尝试做一做,答案放在下面了
位1的个数
class Solution {
public:int hammingWeight(uint32_t n) {int ret = 0;for (int i = 0; i <= 31; i++){if (((n >> i) & 1) == 1){ret++;}}return ret;}
};
比特位计数
class Solution {
public:vector<int> countBits(int n) {//x&(x-1)将x的最右侧的1变成0vector<int> v(n + 1);for (int i = 0; i <= n; i++){int x = i;int count = 0;while (x){count++;x = x & (x - 1);}v[i] = count;}return v;}
};
汉明距离
class Solution {
public:int hammingDistance(int x, int y) {int n = x ^ y;//统计有多少个1int ret = 0;while (n){ret++;n = n & (n - 1);}return ret;}
};
只出现一次的数字
class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for (int i = 0; i < nums.size(); i++){ret ^= nums[i];}return ret;}
};只出现一次的数字iii
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {//目标:将两个单身狗分开,相同的数不拆散,再将两组分别异或//方法:根据两个单身狗任意一个不同的比特位来进行分组int n = 0;for (auto e : nums){n ^= e;}//找到比特位是1的位置--两个单身狗这一位不同int pos = 0;for (int i = 0; i <= 31; i++){if (((n >> i) & 1) == 1) {pos = i;break;}}//根据这一位置的值将所有数分成两组异或int ret1 = 0, ret2 = 0;for (auto e : nums){if (((e >> pos) & 1) == 0){ret1 ^= e;}else{ret2 ^= e;}}return {ret1, ret2};//隐式类型转换}
};相关文章:

【位运算】位运算常用技巧总结
目录 前言 一.常见的小问题 1.给定一个数n,确定它的二进制表示中的第x位是0还是1 2.给定一个数n,将它的二进制表示中的第x位修改成1 3.给定一个数n,将它的二进制表示中的第x位修改成0 4.给定一个数n,提取它的二进制表示中最右侧的1&…...

【STM32】IIC使用中DMA传输时 发送数据总少一个的问题
问题描述 在使用STM32 I2C数据发送过程中,发现每轮实际发送出去的数据总比在DMA配置中设定的传输数据个数要少一个。比方说:DMA配置里设定的传输数据个数是10个,结果发现在总线上只能发出9个,经过进一步发现是少了最后一个数据。…...
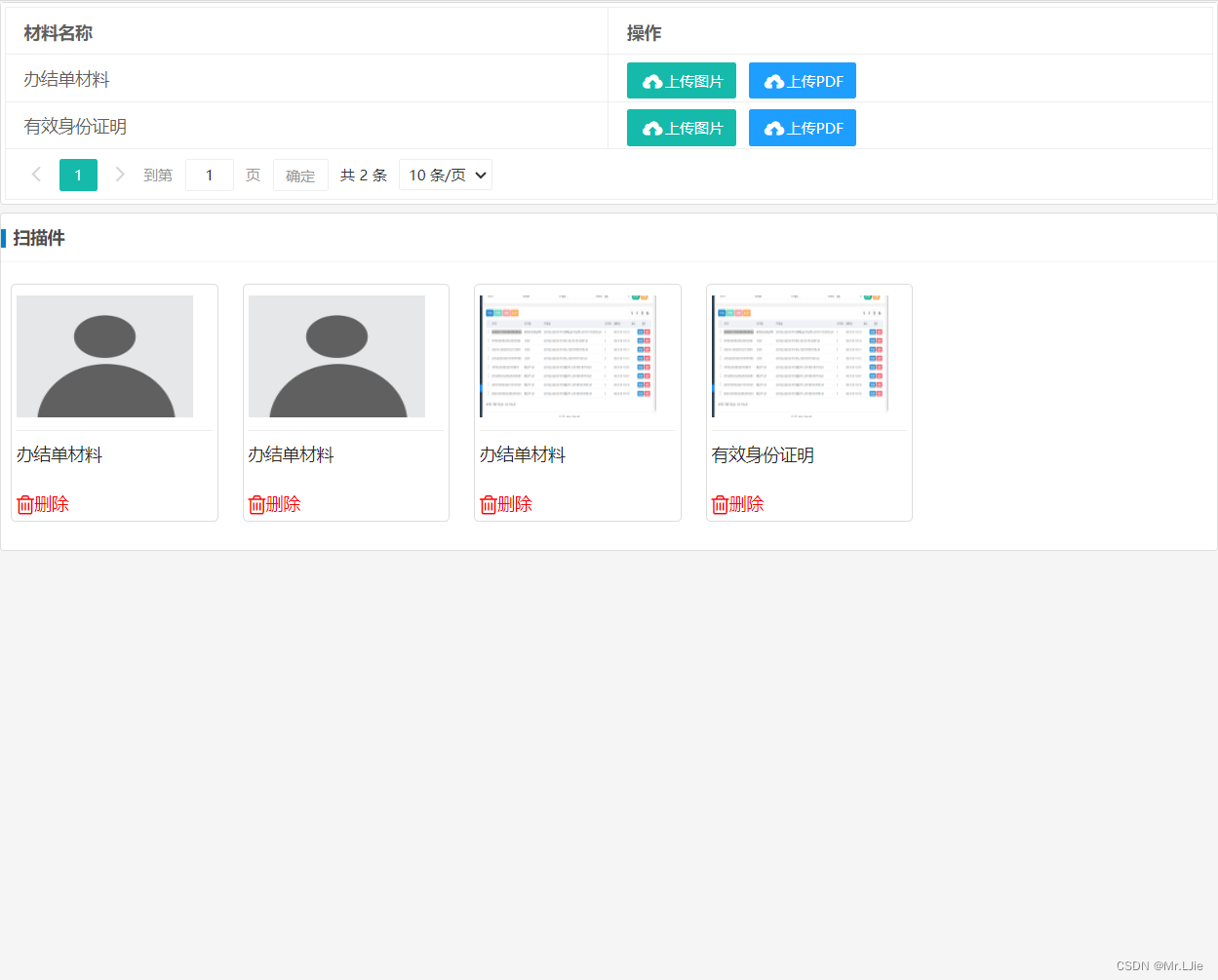
记录layui数据表格使用文件上传按钮
一、前言 虽然用到这种的情况不多,但是还是记录下 二、相关代码 <!DOCTYPE html> <html> <head><meta http-equiv"Content-Type" content"text/html;charsetutf-8"/><meta name"renderer" content&quo…...

c++之枚举
1、背景 在开发代码的过程中,vector类型数组a的index取了一个枚举值CTR,eg:a[CTR],刚开始以为是map类型,后面看不是,简单的看了下c的enum类型,原来enum按顺序默认为数字。 2、enum简介 2.1、…...
LeetCode 热题 100(七):105. 从前序与中序遍历序列构造二叉树、14. 二叉树展开为链表
题目一: 105. 从前序与中序遍历序列构造二叉树https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/ 思路:依据前序遍历的根左右和中序遍历的左根右, 且根左长度=左根 代码: …...

机器学习笔记 - 在表格数据上应用高斯混合GMM和网格搜索GridSearchCV提高分类精度的机器学习案例
1、需求及数据集说明 这是一项二分类任务,评估的是分类准确性(正确预测的标签百分比)。训练集有1000个样本,测试集有9000个样本。你的预测应该是一个9000 x 1的向量。您还需要一个Id列(1到9000),并且应该包括一个标题。格式如下所示: Id,Solution 1,0 2,1 3,1 ... 900…...

【UE 材质】模型部分透明
材质节点如下,这里简单解释一下。首先通过“Mask”节点将"Texture Coordinate" 节点中的“G”通道分离出来,然后通过“if”节点进行判断,当值小于0.5时为透明,当颜色不小于5时为不透明。可以通过一个参数来控制模型透明…...
Web3 社交平台如何脱颖而出?我们和 PoPP 聊了聊
能够颠覆 Web2 传统模式的社交产品有着怎样的特征?PoPP 作为专注于 Web3 的私域流量变现平台,为开发者和用户提供了社交产品发展的新路径,让社区用户充分实现互动交流,着力于创作内容的激励与变现。事实上,面对 Web3 社…...

【Android】ARouter新手快速入门
什么是ARouter ARouter是阿里巴巴推出的一款android界面路由框架 ARouter解决的核心问题是什么 在大型的模块化项目中,一个模块,往往无法直接访问到其它模块中的类,必须通过其它方式来完成模块间的调用 ARouter的核心功能在于,…...

基于VUE3+Layui从头搭建通用后台管理系统(前端篇)十一:通用表单组件封装实现
一、本章内容 本章实现通用表单组件,根据实体配置识别实体属性,并自动生成编辑组件,实现对应数据填充、校验及保存等逻辑。 1. 详细课程地址: 待发布 2. 源码下载地址: 待发布 二、界面预览 三、开发视频 3.1 B站视频地址:...

Oracle Scheduler学习
参考文档: Primary Note: Overview of Oracle Scheduler (Doc ID 1485539.1) Oracle Database Administrators Guide 12c Release 1 (12.1) E17636-21 Chapter(30) Administering Oracle Scheduler Examples of Using the Scheduler http://docs.oracle.com/cd/E166…...
用户体验地图是什么?UX设计心得分享
大家好,我是设计师l1m0身。本篇文章是关于UX设计中的用户体验地图。 对于新手设计师来说,建立用户体验地图会有一些难度。本篇文章中,我会以简单、易懂的语言分享UX设计师如何制作用户体验地图,希望对你的日常项目体验提升有所帮…...

vue3动态路由警告问题
{ path: "/:pathMatch(.*)*", // 必备 component: () > import("/views/error/404.vue"), }, 路由里添加...

17 Linux之大数据定制篇-Shell编程
17 Linux之大数据定制篇-Shell编程 文章目录 17 Linux之大数据定制篇-Shell编程17.1 Shell编程简介17.1.1 为什么要学习Shell编程17.1.2 Shell是什么17.1.3 执行Shell脚本 17.2 Shell的变量17.2.1 Shell变量介绍17.2.2 设置环境变量17.2.3 位置参数变量17.2.4 预定义变量 17.3 …...
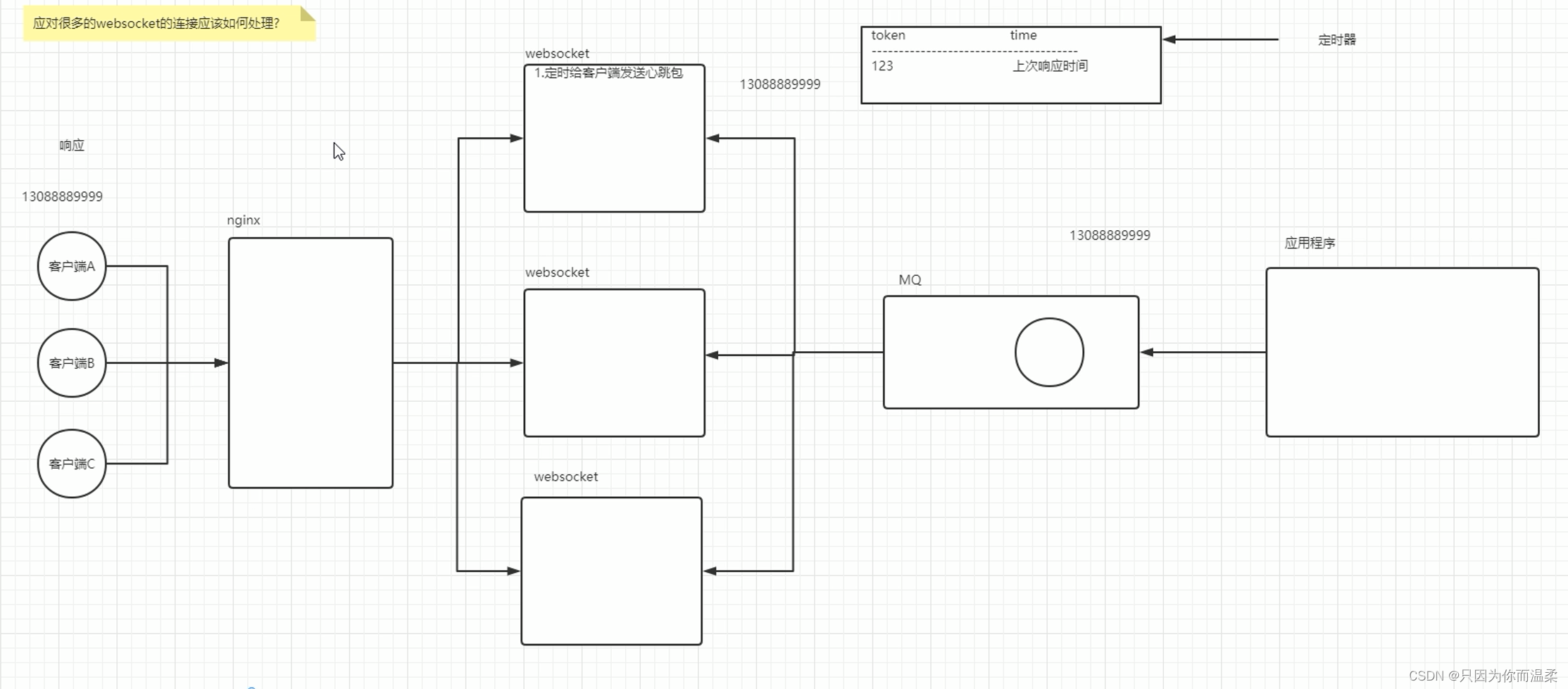
SpringBoot集成WebSocket
SpringBoot集成WebSocket 项目结构图 项目架构图 前端项目 socket.js 注意前端这里的端口是9000, 路劲是ws开头 function createScoket(token){var socket;if(typeof(WebSocket) "undefined") {console.log("您的浏览器不支持WebSocket");}else{var ho…...
Linux服务器部署JavaWeb后端项目
适用于:MVVM前后台分离开发、部署、域名配置 前端:Vue 后端:Spring Boot 这篇文章只讲后端部署,前端部署戳这里 目录 Step1:服务器上搭建后端所需环境1、更新服务器软件包2、安装JDK83、安装MySQL4、登录MySQL5、修…...
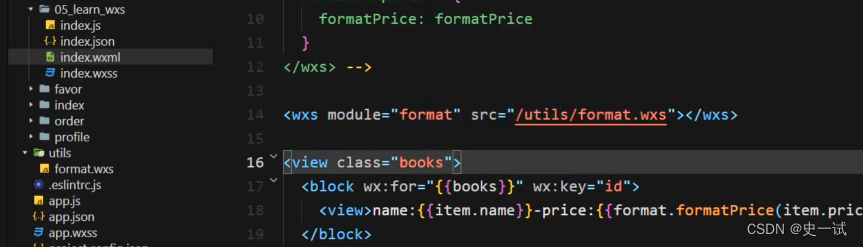
原生小程序 wxs 语法(详细)
WXS WXS(WeiXin Script)是内联在 WXML 中的脚本段。通过 WXS 可以在模版中内联少量处理脚本,丰富模板的数据预处理能力。另外, WXS 还可以用来编写简单的 WXS 事件响应函数。 从语法上看, WXS 类似于有少量限制的 Java…...
和count(1)和count(column)使用比较)
MySQL中count(*)和count(1)和count(column)使用比较
分页查询数据,需要返回total,而这个值一般都是通过count函数实现。但是,针对count函数,有多种写法,如count(*)、count(1) 和 count(column)等。本文主要介绍以上几种写法的差异。 注意,这里仅针对MySQL数据…...

python用 xlwings库对Excel进行 字体、边框设置、合并单元格, 版本转换等操作
xlwings 其他的一些单元格读取写入操作网上很多, 下面就写些如何设置单元格的 字体对齐,字体大小、边框, 合并单元格, 这些设置。 import xlwings as xwapp xw.App(visibleTrue, add_bookFalse) app.display_alerts False #…...
:常用类型)
Golang 中的 archive/zip 包详解(二):常用类型
Golang 中的 archive/zip 包用于处理 ZIP 格式的压缩文件,提供了一系列用于创建、读取和解压缩 ZIP 格式文件的函数和类型,使用起来非常方便。 zip.File 类型 定义如下: type File struct {FileHeaderzip *Readerzipr io…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
