day31 | 455.分发饼干、376. 摆动序列、53. 最大子序和
目录:
解题及思路学习
455. 分发饼干
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
输入: g = [1,2,3], s = [1,1]
输出: 1
思考:看到这个题目,首先想到的是给两个数组排序。然后遍历饼干,双指针找到满足最小胃口的孩子,并且++。 或者先从最大的孩子找,找满足条件的饼干。
根据孩子的胃口来匹配的。
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(), g.end());sort(s.begin(), s.end());int index = s.size() - 1; // 饼干数组的下标int result = 0;for (int i = g.size() - 1; i >= 0; i--) { // 遍历胃口if (index >= 0 && s[index] >= g[i]) { // 遍历饼干result++;index--;}}return result;}
};
根据饼干去匹配孩子的。
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(),g.end());sort(s.begin(),s.end());int index = 0;for(int i = 0; i < s.size(); i++) { // 饼干if(index < g.size() && g[index] <= s[i]){ // 胃口index++;}}return index;}
};
- 时间复杂度:O(nlogn)
- 空间复杂度:O(1)
想清楚局部最优,想清楚全局最优,感觉局部最优是可以推出全局最优,并想不出反例,那么就试一试贪心。
376. 摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 **摆动序列 。**第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
- 例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。 - 相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
示例 1:
输入:nums = [1,7,4,9,2,5]
输出:6
思考:只需要统计数组的峰值就可以了。
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if (nums.size() <= 1) return nums.size();int curDiff = 0; // 当前一对差值int preDiff = 0; // 前一对差值int result = 1; // 记录峰值个数,序列默认序列最右边有一个峰值for (int i = 0; i < nums.size() - 1; i++) {curDiff = nums[i + 1] - nums[i];// 出现峰值if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {result++;preDiff = curDiff; // 注意这里,只在摆动变化的时候更新prediff}}return result;}
};
只需要在 这个坡度 摆动变化的时候,更新 prediff 就行,这样 prediff 在 单调区间有平坡的时候 就不会发生变化,造成我们的误判。
动态规划方法:
memset(dp,0,sizeof(dp));能将数组的每个元素初始化为0
- 设 dp 状态
dp[i][0],表示考虑前 i 个数,第 i 个数作为山峰的摆动子序列的最长长度 - 设 dp 状态
dp[i][1],表示考虑前 i 个数,第 i 个数作为山谷的摆动子序列的最长长度
则转移方程为:
dp[i][0] = max(dp[i][0], dp[j][1] + 1),其中0 < j < i且nums[j] < nums[i],表示将 nums[i]接到前面某个山谷后面,作为山峰。dp[i][1] = max(dp[i][1], dp[j][0] + 1),其中0 < j < i且nums[j] > nums[i],表示将 nums[i]接到前面某个山峰后面,作为山谷。
初始状态:
由于一个数可以接到前面的某个数后面,也可以以自身为子序列的起点,所以初始状态为:dp[0][0] = dp[0][1] = 1。
class Solution {
public:int dp[1005][2];int wiggleMaxLength(vector<int>& nums) {memset(dp, 0, sizeof dp);dp[0][0] = dp[0][1] = 1;for (int i = 1; i < nums.size(); ++i) {dp[i][0] = dp[i][1] = 1;for (int j = 0; j < i; ++j) {if (nums[j] > nums[i]) dp[i][1] = max(dp[i][1], dp[j][0] + 1);}for (int j = 0; j < i; ++j) {if (nums[j] < nums[i]) dp[i][0] = max(dp[i][0], dp[j][1] + 1);}}return max(dp[nums.size() - 1][0], dp[nums.size() - 1][1]);}
};
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4]
输出:6
思考:用一个数记录最大和。for循环遍历,如果当前子序列的和小于0,则重新开始计数。
class Solution {
public:int maxSubArray(vector<int>& nums) {int result = INT32_MIN;int count = 0;for (int i = 0; i < nums.size(); i++) {count += nums[i];if (count > result) { // 取区间累计的最大值(相当于不断确定最大子序终止位置)result = count;}if (count <= 0) count = 0; // 相当于重置最大子序起始位置,因为遇到负数一定是拉低总和}return result;}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
动态规划方法:
class Solution {
public:int maxSubArray(vector<int>& nums) {if (nums.size() == 0) return 0;vector<int> dp(nums.size(), 0);dp[0] = nums[0];int result = dp[0];for (int i = 1; i < nums.size(); i++) {dp[i] = max(dp[i - 1] + nums[i], nums[i]);if (dp[i] > result) result = dp[i];}return result;}
};
- 时间复杂度:O(n)
- 空间复杂度:O(n)
复盘总结
个人反思
1、贪心算法确实比较看能不能想到思路。
2、好像很多都能转成动态规划去做。
相关文章:

day31 | 455.分发饼干、376. 摆动序列、53. 最大子序和
目录: 解题及思路学习 455. 分发饼干 假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。 对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸&#…...

C# textBox 右键菜单 contextMenuStrip
需求: 想在上图空白处可以右键弹出菜单,该怎么做呢? 1.首先,拖出一个 ContextMenuStrip。 随便放哪里都行,如下: 2.在textBox里关联这个“右键控件”即可,如下: 最终效果如下: 以上…...
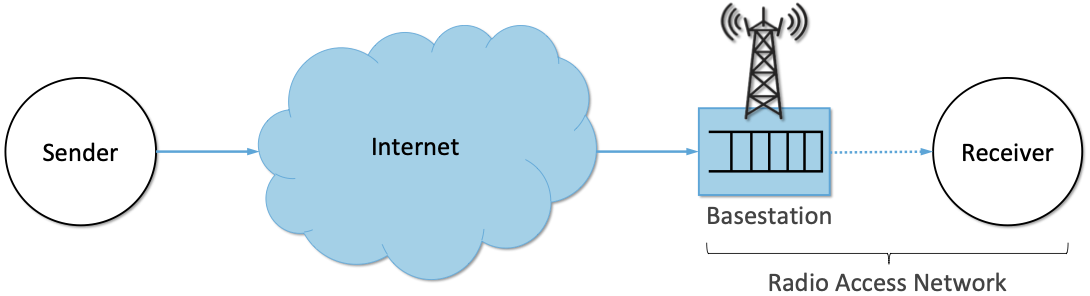
TCP拥塞控制详解 | 7. 超越TCP
网络传输问题本质上是对网络资源的共享和复用问题,因此拥塞控制是网络工程领域的核心问题之一,并且随着互联网和数据中心流量的爆炸式增长,相关算法和机制出现了很多创新,本系列是免费电子书《TCP Congestion Control: A Systems …...
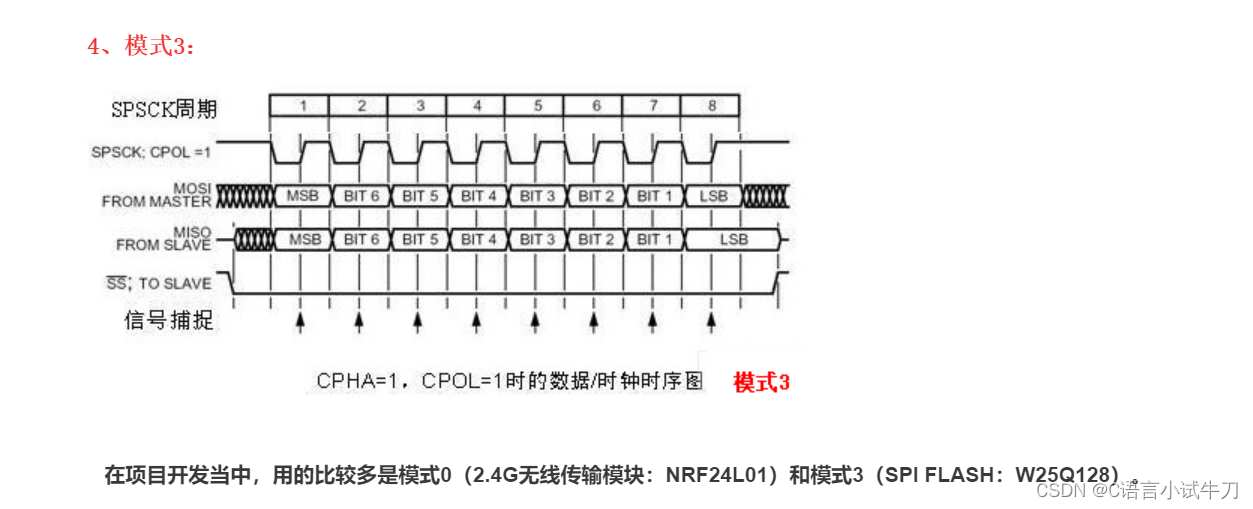
stm32之26.spi外设
...
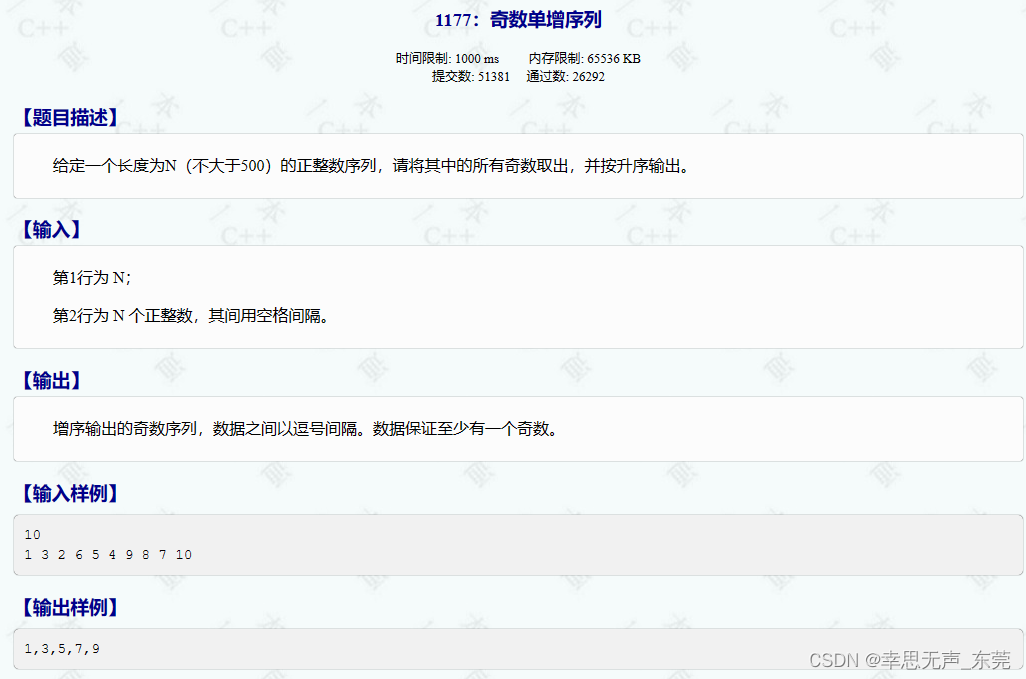
C++信息学奥赛1177:奇数单增序列
#include<bits/stdc.h> using namespace std; int main(){int n;cin>>n; // 输入整数 n,表示数组的大小int arr[n]; // 创建大小为 n 的整型数组for(int i0;i<n;i) cin>>arr[i]; // 输入数组元素for(int i0;i<n;i){ // 对数组进行冒泡排序f…...
Java的数组是啥?
1.数组是啥? 数组是一块连续的内存,用来存储相同类型的数据 (1)如何定义数组? 1.int[] array {1,2,3,4} new int[]{1,2,3,4};//这里的new是一个关键字,用来创建对象 2.数组就是一个对象 动态初始化 …...
)
我的私人笔记(安装hadoop)
1.安装hadoop01环境 注需安装最小安装和使用英文界面 2.安装群集 // 获得网关IP:192.168.80.2 获得子网掩码:255.255.255.0 // 获得网段:[起始IP地址]192.168.128 --- [结束IP地址]192.168.80.254 // 计划集群的ip和主机名 //192.168.80.…...
【板栗糖GIS】——360浏览器的下载图标隐藏在内部不方便,怎么修改
目录 1. 设置前的本来样子 2. 登录360的皮肤中心 3. 使用se13的经典皮肤 最近edge浏览器最近使用bilibili和notion都非常卡,时不时崩溃,不得不换浏览器使用,试来试去360浏览器最得我心,只不过广告太多,调教也是花了…...

SpringMVC之文件上传和下载
文章目录 前言一、文件下载二、文件上传总结 前言 实现下载文件和上传文件的功能。 一、文件下载 使用ResponseEntity实现下载文件的功能 RequestMapping("/testDown") public ResponseEntity<byte[]> testResponseEntity(HttpSession session) throws IOEx…...

简单了解OSI网络模型
目录 一、协议是什么? 二、OSI七层模型 三、TCP/IP五层模型 一、协议是什么? 协议顾名思义就是通过大家伙一起协商讨论达成的统一规则和标准。网络协议就是规定用户数据信息如何在网络上传播以及实现某种网络技术所要遵循的统一标准和规则。 二、OSI…...

服务网格实施周期缩短 50%,丽迅物流基于阿里云 ACK 和 ASM 的云原生应用管理实践
作者:王夕宁、 刘强、 华相 公司介绍 丽迅物流是百丽旗下专注于时尚产业、为企业提供专业物流及供应链解决方案的服务商。其产品服务主要包括城市落地配、仓配一体、干线运输及定制化解决方案。通过自研智能化物流管理平台,全面助力企业合作集约化发展…...

bpmnjs Properties-panel拓展(属性设置篇)
最近有思考工作流相关的事情,绘制bpmn图的工具认可度比较高的就是bpmn.js了,是一个基于node.js的流程图绘制框架。初始的框架只实现了基本的可视化,想在xml进行客制化操作的话需要拓展,简单记录下几个需求的实现过程。 修改基础 …...

Debian系统上通过NFS挂载远程服务器硬盘
步骤 1:配置远程服务器 在拥有硬盘内容的远程服务器上,进行以下配置: 安装NFS服务器软件: sudo apt-get update sudo apt-get install nfs-kernel-server编辑NFS服务器配置文件 /etc/exports,添加需要共享的目录及其权…...
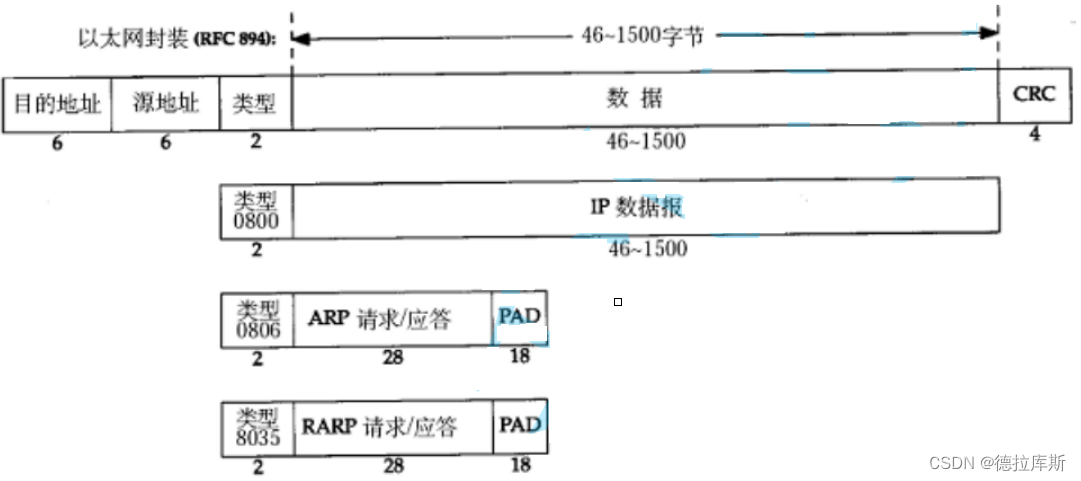
【Linux】以太网协议以及MTU
以太网协议 数据链路层的功能以太网的数据格式MTUMTU对IP协议的影响MTU对UDP协议的影响MTU对TCP协议的影响 数据链路层的功能 数据链路层的主要功能是:控制链路。包括数据链路的建立、链路的维护和释放。MAC寻址也是它的功能,寻址是指计算机网卡的MAC地…...
UE5打完包后,启动程序不能全屏
最近看到ue5的打包程序后不能默认自动全屏,效果如下,发现并不是全屏的,而且就算点击放大也不是全屏 解决办法:设置如下之后在打包就可以了 但是会一直打印错误的日志,不过这个不影响使用...

财务部发布《企业数据资源相关会计处理暂行规定》
导读 财务部为规范企业数据资源相关会计处理,强化相关会计信息披露,根据《中华人民共和国会计法》和相关企业会计准则,制定了《企业数据资源相关会计处理暂行规定》。 加gzh“大数据食铁兽”,回复“20230828”获取材料完整版 来…...

引用(个人学习笔记黑马学习)
1、引用的基本语法 #include <iostream> using namespace std;int main() {int a 10;//创建引用int& b a;cout << "a " << a << endl;cout << "b " << b << endl;b 100;cout << "a "…...

卷积神经网络实现运动鞋识别 - P5
🍨 本文为🔗365天深度学习训练营 中的学习记录博客🍦 参考文章:Pytorch实战 | 第P5周:运动鞋识别🍖 原作者:K同学啊 | 接辅导、项目定制🚀 文章来源:K同学的学习圈子 目录…...
C#安装“Windows 窗体应用(.NET Framework)”
目录 背景: 第一步: 第二步: 第三步: 总结: 背景: 如下图所示:在Visual Studio Installer创建新项目的时候,想要添加windows窗体应用程序,发现里面并没有找到Windows窗体应用(.NET Framework)模板,快捷搜索也没有发现&#…...
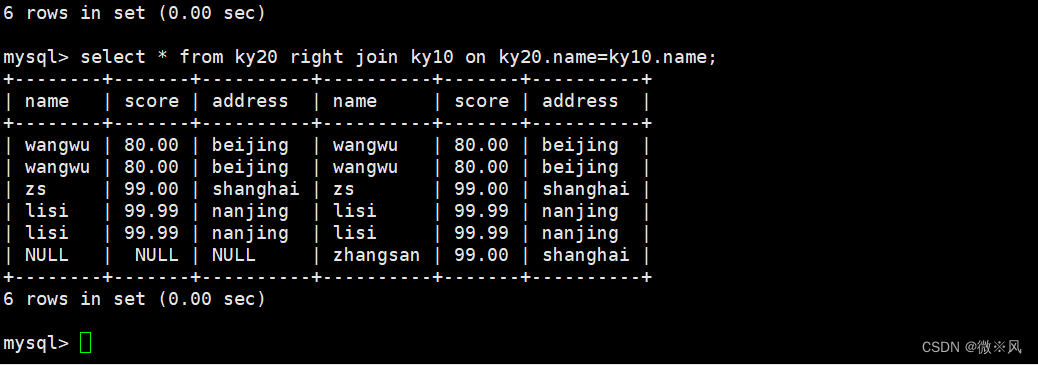
SQL高阶语句
目录 1、概念 1.1、概述 1.2、常见的MySQL高阶语句的概念: 1.3、 SQL高阶语句的作用 2、常用查询 2.1、按关键字排序 2.1.1、概述和作用 2.1.2、 (1)语法 2.1.3、模板表:ky30 编辑2.1.4、分数按降序排列 2.1.5、ORDER…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
