《算法竞赛·快冲300题》每日一题:“简化农场”
《算法竞赛·快冲300题》将于2024年出版,是《算法竞赛》的辅助练习册。
所有题目放在自建的OJ New Online Judge。
用C/C++、Java、Python三种语言给出代码,以中低档题为主,适合入门、进阶。
文章目录
- 题目描述
- 题解
- C++代码
- Java代码
- Python代码
“ 简化农场” ,链接: http://oj.ecustacm.cn/problem.php?id=1879
题目描述
【题目描述】 约翰的农场可以看做一个图,农田代表图中顶点,田间小路代表图中的边,每条边有一定的长度。
约翰发现自己的农场中最多有三条小路有着相同的长度。
约翰想删除一些小路使得农场成为一棵树,使得两块农田间只有一条路径。
约翰想把农场设计成最小生成树,也就是农场道路的总长度最短。
请帮助约翰找出最小生成树的总长度,同时请计算出总共有多少种最小生成树。
【输入格式】 输入第一行为两个正整数 N 和 M ,表示点数和边数(1 <= N <= 40,000; 1 <= M <= 100,000)。
接下来 M 行,每行三个整数 ai, bi, ci,表示点 ai 和 bi 之间存在长度为 ci 的无向边。(1 <= ai, bi <= N; 1 <= ci <= 1,000,000)
【输出格式】 输出一行包含两个整数,分别表示最小生成树的长度和最小生成树的数目。
数目对 1,000,000,007 求余.
【输入样例】
4 5
1 2 1
3 4 1
1 3 2
1 4 2
2 3 2
【输出样例】
4 3
题解
有两种最小生成树(MST)算法:kruskal、prim。Kruskal的思路是对边贪心,“最短的边一定在MST上”;prim的思路是对点贪心,“最近的邻居点一定在MST上”。
本题描述中比较特殊的地方是:(1)最多有三条小路(边)有相同长度;(2)计算总共有多少种最小生成树。着重点在边上,所以用kruskal算法。
kruskal算法执行步骤是:(1)对边排序;(2)从最短的边开始,从小到大依次把边加入到MST中;(3)加边的过程中用并查集判断是否产生圈,如果形成了圈就丢弃这个边;(4)所有边处理完后结束,或者加边的数量等于n-1时结束。
如果所有的边长都不同,那么只有一种最小生成树。题目指出“最多有三条边的长度相同”,从样例可知,有等长的两条边,也有等长的三条边。对边排序时,这些相等的边会挨在一起。
处理等长边,设cnt是合法(所谓合法,是指这个边加入到MST,不会产生圈)的边的数量,num是这几个等长边有几个能同时加入到MST。sum是最小生成树的数目。
(1)有两条等长边。
若cnt=1,只有一条边是合法的,也就是说这条边别无选择,那么sum不变。
若cnt=2,有2条边合法,继续讨论:
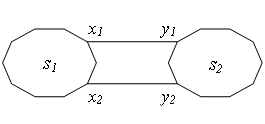
1)num=1,即这两条等长边只有一条能加入到MST中。那么sum = sumcnt,即sum=sum2。以下图为例,s1和s2是两棵已经加入到MST的子树,它们内部没有圈。现在加两条等长边(x1,y1)、(x2,y2),它们单独加入MST都是合法的,但是同时加入就会形成圈。
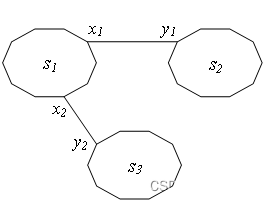
2)num=2,即这两条等长边都应该加入到MST中。那么sum不变,即sum=sum1。以下图为例。
(2)有三个等长边。
若cnt=1,只有一条边合法,sum不变。
若cnt=2,有两条边合法,和(1)有两条等长边,且cnt=2的情况一样。
若cnt=3,有三条边合法,那么:
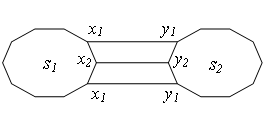
1)num = 1,只有一条边能加入到MST中,sum = sumcnt=sum3。以下图为例,三条边任选一条,有3种情况。
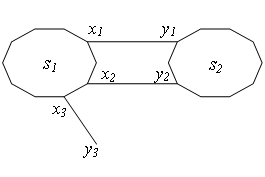
2)num = 2,有两条边能加入到MST中,且其中一条边必须加,sum = sum2。以下图为例,三条边任选两条,有2种情况。
3)num = 2,有两条边能加入到MST中,且是任意两条,sum = sum*3。以下图为例,三条边任选两条,有3种情况。
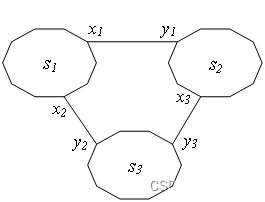
3)num = 3,三条边都应该加入到MST中,sum不变。
【重点】 kruskal 。
C++代码
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N = 1e6+10;
const int mod = 1e9+7;
struct Node{int x,y,val;}e[N<<1];
bool cmp(Node a,Node b){return a.val<b.val;}//按边权排序
int n,m;
int s[N]; //并查集
int ans=0,sum=1; //ans: MST的总长度, sum:最小生成树的数目
int find_set(int x){ //查询并查集,返回x的根if(x != s[x]) s[x] = find_set(s[x]); //路径压缩return s[x];
}
void kruscal(){for(int i=1;i<=n;i++) s[i] = i; //并查集初始化sort(e+1,e+m+1,cmp); //边:升序排序for(int i=1;i<=m;){ //遍历所有边,每次处理其中的等长边int cnt = 0; //这次的等长边中,有几个可以加入MSTset<pair<int,int> >st; //set用于存储并去重int j; //第i~j个边等长for(j=i;j<=i+2 && e[i].val==e[j].val;j++){ //枚举等长边,最多3个相同。更新jint s1 = find_set(e[j].x); //边的一个端点属于哪个集?int s2 = find_set(e[j].y); //边的另一个端点属于哪个集?if(s1 > s2) swap(s1,s2);if(s1 != s2){ //两个集不等,这个边可以加入到MST中cnt ++; //cnt: 允许加入MST的边的数量st.insert(make_pair(s1,s2)); //这个边的两端点所属的集存到st中}} //第i~j个边是等长的int num = 0;for(;i<j;i++){ //开始时第i~j个边是等长的。i=j时退出int s1 = find_set(e[i].x);int s2 = find_set(e[i].y);if(s1 != s2){ //不属于一个集,可以加入到树里s[s2] = s1; //并查集合并num++; //这几个等长边有num个可以同时加入树}}ans += e[i-1].val*num; //这几个等长边最后有num个可以加入到MST,计算MST总长if(num == 1) sum = sum*cnt%mod; //只有一条边能加入树,直接乘以cntif(cnt == 3 && num==2 && st.size() == 2) sum = 2*sum%mod;if(cnt == 3 && num==2 && st.size() == 3) sum = 3*sum%mod;//其他情况方案数都不变}
}
signed main(){scanf("%lld%lld",&n,&m); //读点,边for(int i=1;i<=m;i++) //存边,用最简单的“边集数组”存边scanf("%lld%lld%lld",&e[i].x,&e[i].y,&e[i].val);kruscal(); //最小生成树printf("%lld %lld\n",ans,sum);
}
Java代码
Python代码
相关文章:

《算法竞赛·快冲300题》每日一题:“简化农场”
《算法竞赛快冲300题》将于2024年出版,是《算法竞赛》的辅助练习册。 所有题目放在自建的OJ New Online Judge。 用C/C、Java、Python三种语言给出代码,以中低档题为主,适合入门、进阶。 文章目录 题目描述题解C代码Java代码Python代码 “ 简…...

【二等奖方案】大规模金融图数据中异常风险行为模式挖掘赛题「冀科数字」解题思路
第十届CCF大数据与计算智能大赛(2022 CCF BDCI)已圆满结束,大赛官方竞赛平台DataFountain(简称DF平台)正在陆续释出各赛题获奖队伍的方案思路,欢迎广大数据科学家交流讨论。 本方案为【大规模金融图数据中…...
方法查询速度比较)
C# List与HashSet的contains()方法查询速度比较
List 和HashSet同时查询40万条数据,谁的效率更高? //**1.下面是List底层源码**public boolean contains(Object o) {//如果查到我们想要查询的值则返回一个true,否则返回false,return indexOf(o) > 0;//这里是调用了indexOf方…...
命令执行漏洞复现攻击:识别威胁并加强安全
环境准备 这篇文章旨在用于网络安全学习,请勿进行任何非法行为,否则后果自负。 一、攻击相关介绍 原理 主要是输入验证不严格、代码逻辑错误、应用程序或系统中缺少安全机制等。攻击者可以通过构造特定的输入向应用程序或系统注入恶意代码ÿ…...

Keepalived实现服务器的高可用性
目录 背景方案简介KeepalivedHeartbeat Keepalived技术介绍Keepalived通信方式时间同步 Keepalived配置案例Keepalived日志配置Keepalived服务配置全局配置段VRRP配置段Keepalived服务启动 服务异常检测 背景 在实际应用中,为了提高服务器的高可用性,往…...

Python程序化交易接口批量获取数据源码
小编举例下面是一个简单的示例代码,展示如何使用Python的程序化交易接口批量获取数据,例如开发文档参考:MetaTradeAPI (metatradeapi) - Gitee.com 签名 int Init(); 功能 API 初始化 参数 无 返回值 授权成功的交易账户数量 返回值 &…...

【强化学习】基本概念
基本大概框架 强化学习的主要角色是 智能体 (agent)和 环境,环境是智能体存在和互动的世界。智能体根据当前的环境做出action,action影响环境。然后智能体根据新的环境再进行action。 基础用语 状态(state, s)&…...

0001__安装electron失败 postinstall: `node install.js`
不一样的 npm 快速安装electron的方案 - 简书 2、手动下载出错的文件 打开浏览器输入 下述网址, 找到你要的版本号, 点击后找到你的平台点击即可下载了。https://registry.npmmirror.com/binary.html?pathelectron/ 作者:一颗人心 链接&…...
Linux测开常用命令总结
文章目录 Linux系统中文件目录树 基本指令的使用: Linux命令的帮助信息查看 --help command --help 说明: 显示command 命令的帮助信息通过man命令查看帮助信息 man command( 命令的名称) man 命令查看的帮助信息更加详细ls,pwd,…...

xml转化为txt数据的脚本,为yolo提供训练
这里写自定义目录标题 xml转化为txt数据的脚本 xml转化为txt数据的脚本 代码如下: import xml.etree.ElementTree as ET import os, cv2 import numpy as np from os import listdir from os.path import joinclasses []def convert(size, box):dw 1. / (size[0…...

【H5页面嵌入到小程序或APP中实现手机号点击复制和拨号功能】
在H5界面嵌入到小程序和移动应用(安卓和iOS)中实现手指点击手机号弹出弹窗,包含呼叫和复制选项,是可以实现的。下面我将为你提供一个基本的示例,并解释在小程序、安卓和iOS中要做的支持工作。 <!DOCTYPE html> …...

Kubernetes技术--k8s核心技术 configMap
1.概述 configMap最主要的作用是存储一些不加密的数据到/etcd,让pod以变量或者数据卷(volume)挂载到容器。 应用场景:配置文件、存储信息等 2.使用 -1.创建配置文件。 这里我们需要先编写一个配置文件。使用redis,如下所示:...

Springboot动态修改日志级别
在开发和运维过程中,我们经常需要调整日志级别来查看不同级别的日志信息。传统的做法是修改配置文件,然后重启应用程序。但是,在分布式系统中,重启应用程序可能比较麻烦,而且也影响了业务的正常运行。 Springboot提供…...

新手将最简单的springboot部署上tomcat出现的意外问题
现阶段springboot部署到tomcat的文章一抓一大把且都相同,便贴一个地址以展示流程: SpringBoot打war包部署Tomcat(最全)_spring boot war 部署tomcat_聊Java的博客-CSDN博客 那么就说一下我出现的问题: 在完整复现流程且确认代码无误的情况下,部署到tomcat,此时问题出现了:启动…...
)
P1177 【模板】排序(Sort排序)
题目描述 将读入的 N N N 个数从小到大排序后输出。 输入格式 第一行为一个正整数 N N N。 第二行包含 N N N 个空格隔开的正整数 a i a_i ai,为你需要进行排序的数。 输出格式 将给定的 N N N 个数从小到大输出,数之间空格隔开,…...
软件测试(黑盒测试、白盒测试、灰盒测试)
软件测试方法大类上分为黑盒测试、白盒测试和灰盒测试三种 一、黑盒测试 黑盒测试通俗来说即不知道代码是怎么写的。具体实现逻辑,基于代码输入有哪些应该输出什么进行测试的方法。其方法有:基于直觉和经验的方法(IEBT)、基于需…...

昨天面试的时候被提问到的问题集合。
1、vue的双向绑定原理是什么?里面的关键点在哪里? 2、实现水平垂直居中的方式? 3、常用伪元素有哪一些? 4、移动端如何适配不同屏幕尺寸? 5、本地存储有哪一些?他们三者有什么区别? 6、JS的数据…...
广电运营商三网融合监控运维方案
随着三网融合逐步发展、深化,广电网络从为用户提供原本单一的信息服务转向了集语音、文字、图像为一体的信息服务,同时也实现了由单一独立的网络向综合性网络的改变。如何在业务的融合与竞争中创造核心竞争力,利用自身网络覆盖率上的优势&…...

数据库锁简析
数据库大并发操作要考虑死锁和锁的性能问题。用T1代表一个数据库执行请求,T2代表另一个请求,也可以理解为T1为一个线程,T2 为另一个线程。T3,T4以此类推。下面以SQL Server为例。 锁的种类 共享锁(Shared lock) 例1:T1: select…...
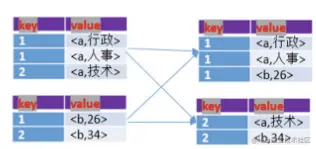
说说广播流与普通流
分析&回答 user actions 可以看作是事件流(普通流)patterns 为广播流,把全量数据加载到不同的计算节点。 广播流 Broadcast是一份存储在TaskManager内存中的只读的缓存数据在执行job的过程中需要反复使用的数据,为了达到数据共享&am…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

面试高频问题
文章目录 🚀 消息队列核心技术揭秘:从入门到秒杀面试官1️⃣ Kafka为何能"吞云吐雾"?性能背后的秘密1.1 顺序写入与零拷贝:性能的双引擎1.2 分区并行:数据的"八车道高速公路"1.3 页缓存与批量处理…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

跨平台商品数据接口的标准化与规范化发展路径:淘宝京东拼多多的最新实践
在电商行业蓬勃发展的当下,多平台运营已成为众多商家的必然选择。然而,不同电商平台在商品数据接口方面存在差异,导致商家在跨平台运营时面临诸多挑战,如数据对接困难、运营效率低下、用户体验不一致等。跨平台商品数据接口的标准…...
