【LeetCode】3. 无重复字符的最长子串
3. 无重复字符的最长子串(中等)


方法:滑动窗口 + 哈希表
思路
-
这道题主要用到思路是:滑动窗口
-
什么是滑动窗口?
-
其实就是一个队列,比如例题中的 abcabcbb,进入这个队列(窗口)为 abc 满足题目要求,当再进入 a,队列变成了 abca,这时候不满足要求。所以,我们要移动这个队列!
-
如何移动?
-
我们只要把队列的左边的元素移出就行了,直到满足题目要求!
-
一直维持这样的队列,找出队列出现最长的长度时候,求出解!
代码
class Solution {
public:int lengthOfLongestSubstring(string s) {int ans = 0;int left = 0;unordered_set<char> lookup;for(int i=0; i<s.size(); ++i) {// 说明该字符重复.// 不断删除最左边的元素,直到将重复元素移出窗口while(lookup.find(s[i]) != lookup.end()) {lookup.erase(s[left]);left ++;}ans = max(ans, i - left + 1);lookup.insert(s[i]);}return ans;}
};
参考资料
- 滑动窗口
相关文章:

【LeetCode】3. 无重复字符的最长子串
3. 无重复字符的最长子串(中等) 方法:滑动窗口 哈希表 思路 这道题主要用到思路是:滑动窗口 什么是滑动窗口? 其实就是一个队列,比如例题中的 abcabcbb,进入这个队列(窗口)为 ab…...
苹果macOS 14开发者预览版Beta 7发布 新增超过100款视频壁纸和屏保
8 月 31 日,苹果向 Mac 电脑用户推送了 macOS 14 开发者预览版 Beta 7 更新(内部版本号:23A5337a),本次更新距离上次发布隔了 8 天。 苹果发布 Beta 7 更新的同时,还发布了第 6 个公测版,正式版…...
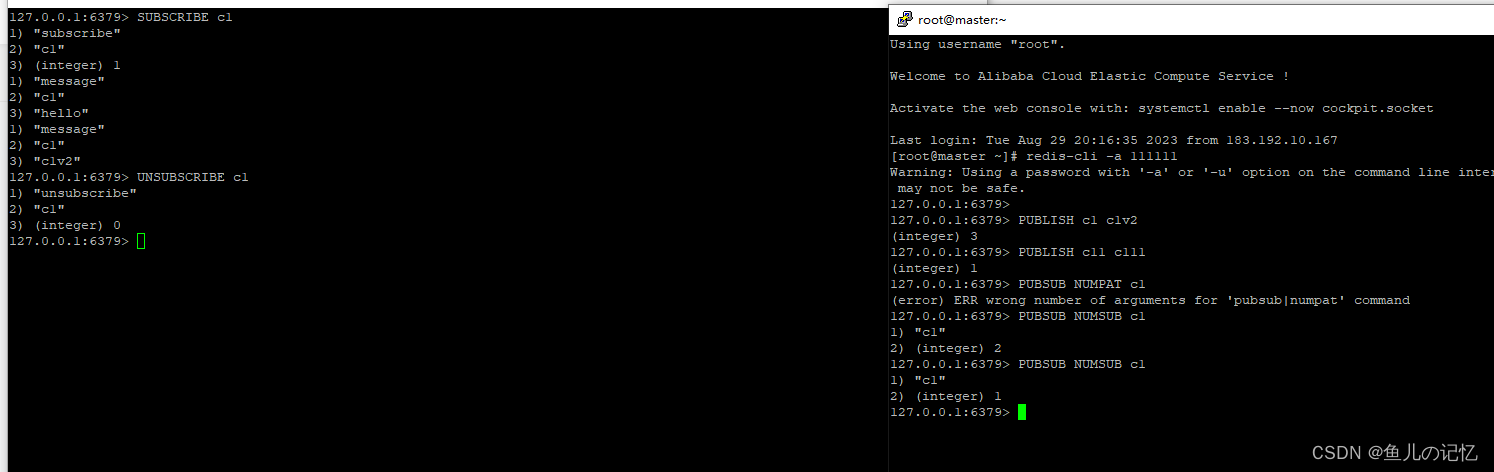
Redis 7 第五讲 事务、管道、发布订阅 过渡篇
事务 理论 可以一次执行多个命令,本质是一组命令的集合。一个事务中的所有命令都会序列化,按顺序地串行化执行而不会被其它命令插入,不许加塞 一个队列中,一次性、顺序性、排他性的执行一系列命令 Redis事务 VS 关系型数据库事务…...
[SpringBoot3]视图技术Thymeleaf
七、视图技术Thymeleaf Thymeleaf是一个表现层的模板引擎,一般被使用在Web环境中,它可以处理HTML、XML、JS等文档,简单来说,它可以将JSP作为Java Web应用的表现层,有能力展示与处理数据。这样,同一个模板文…...

wangluobiancheng
UDP send: receive: TCP...
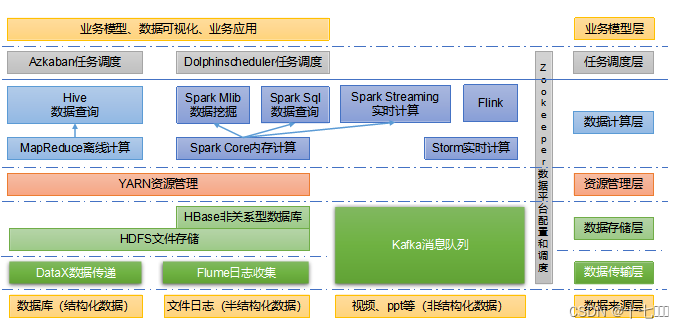
大数据之hadoop入门
大数据概念 大数据:无法在一定时间范围内用常规软件工具进行捕捉、管理和处理的数据集合,是需要新处理模式才能具有更强的决策力、洞察发现李和流程优化能力的海量、高增长率和多样化的信息资产。 大的概念是相对来说的:目前来说࿰…...

浅谈多人游戏原理和简单实现。
😜作 者:是江迪呀✒️本文关键词:websocket、网络、原理、多人游戏☀️每日 一言:这世上有两种东西无法直视,一是太阳,二是人心! 一、我的游戏史 我最开始接触游戏要从一盘300游戏…...

活动预告 | 龙智、紫龙游戏与JFrog专家将出席龙智DevSecOps研讨会,探讨企业大规模开发创新
2023年9月8日(周五)下午13:30-19:45,龙智即将携手Atlassian与JFrog在上海共同举办主题为“大规模开发创新:如何提升企业级开发效率与质量”的线下研讨会。 在此次研讨会上,龙智高级咨询顾问、Atlassian认证专家叶燕秀…...

米每秒和千米每小时的换算
千米每时和米每秒怎么换算?1米/秒3600米/3600秒 米每秒和千米每小时的换算(米每秒和千米每小时的换算) 3.6千米/小时。 3.6千米/小时1米/秒米每秒和千米每小时的换算1 米/秒(米每秒)3.6 千米/时(千米每小时)。 1米每秒3600米每时3.6千米每时。因为1小时3600秒。小时是一个时…...

js实现图形验证码
图形验证码起什么作用: 可以防止:恶意破解密码、刷票、论坛灌水,有效防止某个黑客对某一个特定注册用户用特定程序暴力破解方式进行不断的登录尝试。 验证码一般是防止批量注册的,人眼看起来都费劲,何况是机器。不少…...

一句话画出动漫效果
链接: AI Comic Factory - a Hugging Face Space by jbilcke-hfDiscover amazing ML apps made by the communityhttps://huggingface.co/spaces/jbilcke-hf/ai-comic-factory 选择类型: Japanese 输入提示词: beauty and school love st…...

【openGauss2.1.0 TPC-C数据导入】
openGauss2.1.0 TPC-C数据导入 一、下载tpch测试数据二、导入测试数据 一、下载tpch测试数据 使用普通用户如omm登录服务器执行如下命令下载测试数据库:git clone https://gitee.com/xzp-blog/tpch-kit.git二、导入测试数据 进入dbgen目录下,生成makef…...

vue+elementui表格导出
htmlToExcel.js import FileSaver from file-saver import XLSX from xlsxconst htmlToExcel {getExcel(dom, title 默认标题) {var excelTitle titlevar wb XLSX.utils.table_to_book(document.querySelector(dom))/* 获取二进制字符串作为输出 */var wbout XLSX.write(w…...

掌握前端利器:JavaScript页面渲染高阶方法解析与实战
引言 前端开发中,页面渲染的速度和质量是衡量一个开发者水平的重要标准。而在众多的前端技术中,JavaScript以其强大的页面渲染能力独占鳌头。本文将深入探讨JavaScript在页面渲染中的应用,并通过实例展示其高阶方法,旨在帮助读者…...
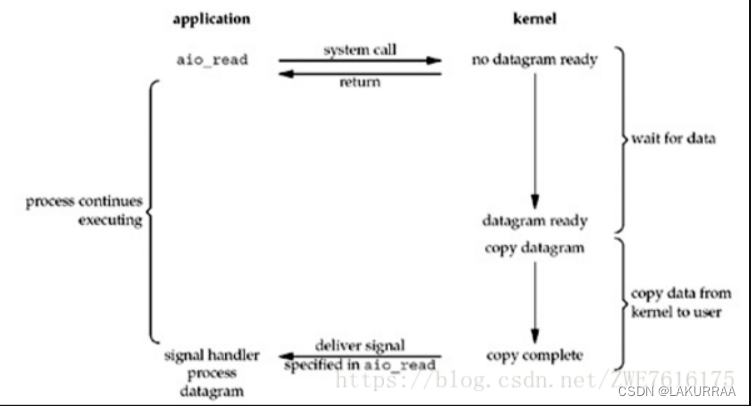
面试题——网络IO模型
一、socket socket是在应用层和传输层中间的抽象层,它把传输层(TCP/UDP)的复杂操作抽象成一些简单的接口,供应用层调用实现进程在网络中的通信。Socket起源于UNIX,在Unix一切皆文件的思想下,进程间通信就被…...
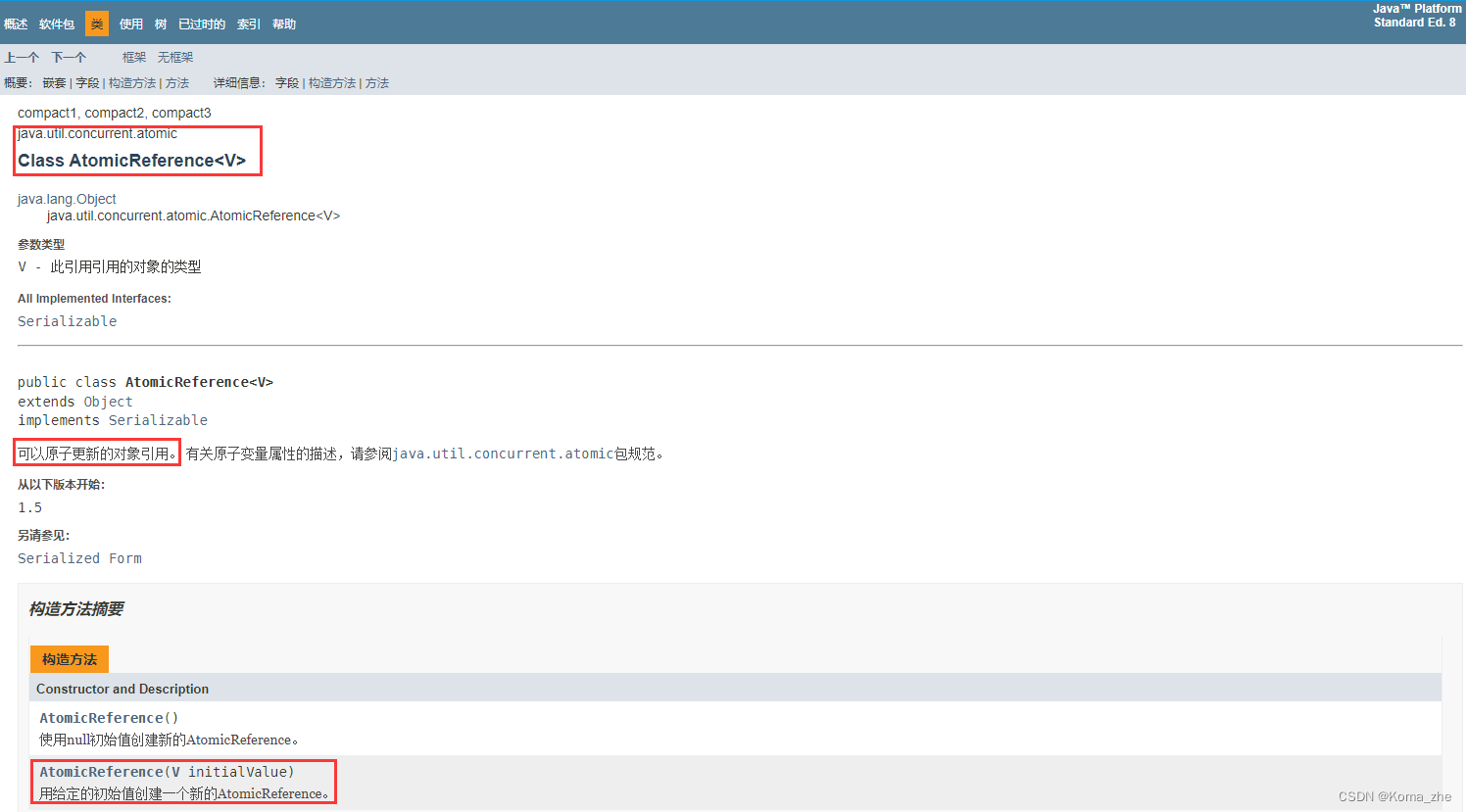
【JUC基础】JUC入门基础(二)
目录 异步回调JMM 理解对 volatile 的理解1、保证可见性2、不保证原子性3、禁止指令重排 对 JMM 的理解 详解单例模式饿汉式懒汉式DCL懒汉式:双重检测锁模式的懒汉式单例静态内部类实现单例通过反射破坏单例,修改后的DCL饿汉式枚举实现单例防止反射破坏 …...
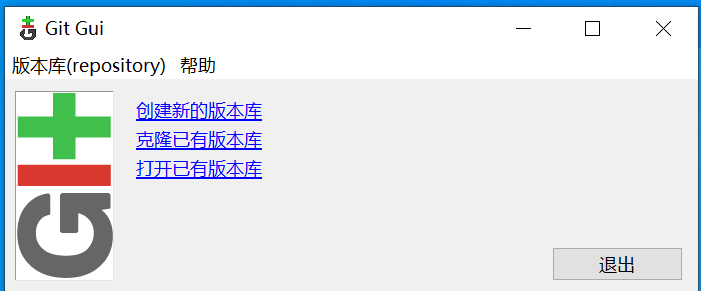
Git Bash 和 Git GUI中文汉化
目录 为什么要中文汉化?Git Bash的汉化Git GUI的汉化 为什么要中文汉化? 看到中文大概能猜出是什么意思,便于使用,特别是Git GUI,中文版的菜单很容易理解是要做什么,如下图: Git Bash的汉化 …...

【Ubuntu】Ubuntu常用软件部署
1.安装jdk1.8 (1).apt方式安装 1).安装 1.在终端中输入以下命令,以更新软件包列表 sudo apt-get update2.在终端中输入以下命令,以安装JDK 1.8 sudo apt-get install openjdk-8-jdk3.将Java 1.8设置为默认版本。在终端中输入以下命令 sudo update-…...

Hadoop HA模式切换
Hadoop HA模式下 主从的切换(操作命令) YARN HA 获取所有RM节点的状态 yarn rmadmin -getAllServiceState获取 rm1 节点的状态 yarn rmadmin -getServiceState rm1手动将 rm1 的状态切换到STANDBY yarn rmadmin -transitionToStandby rm1 ##或者 y…...

自然语言处理(四):全局向量的词嵌入(GloVe)
全局向量的词嵌入(GloVe) 全局向量的词嵌入(Global Vectors for Word Representation),通常简称为GloVe,是一种用于将词语映射到连续向量空间的词嵌入方法。它旨在捕捉词语之间的语义关系和语法关系&#…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
