算法系列-876-求链表的中间节点
求链表中间节点,如果有两个中间节点取后面那个
链表定义
// @lc code=start
/*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val = val; }* ListNode(int val, ListNode next) { this.val = val; this.next = next; }* }*/
方法一:计数取一半
解题方法:
先计算链表一共有多少个节点n
n/2,得到中间节点的下标(从0开始)
1 -> 2 -> 3 -> 4 -> 5
坐标节点就是链表的中间节点
时间复杂度:O(n)
空间复杂度:O(1)
public ListNode middleNode(ListNode head) {/*** 先计算链表一共有多少个节点n* n/2,得到中间节点的下标(从0开始)* 1 -> 2 -> 3 -> 4 -> 5* 坐标节点就是链表的中间节点* */int n=0;ListNode p=head;while (p!=null){n++;p=p.next;}int mid=n/2;ListNode midNode=head;for (int i = 0; i < mid; i++) {midNode=midNode.next;}return midNode;}
方法二:双指针
解题方法:
定义快慢两个指针,快指针每次移动2步,慢指针每次移动1步
注意:指针需要从头节点前开始移动,因此需要定义一个哑结点,快指针和慢指针都从哑节点开始
当快指针移动了2k步后,慢指针移动了k步
假设2k=n,k=n/2
当n为偶数时,慢指针的后续节点就是中间节点
当n为奇数时,慢指针就是中间节点
是否是偶数节点看快指针每次是否都能移动两步
时间复杂度:O(n)
空间复杂度:O(1)
public ListNode middleNode(ListNode head) {/*** 定义快慢两个指针,快指针每次移动2步,慢指针每次移动1步* 注意:指针需要从头节点前开始移动,因此需要定义一个哑结点,快指针和慢指针都从哑节点开始* 当快指针移动了2k步后,慢指针移动了k步* 假设2k=n,k=n/2* 当n为偶数时,慢指针的后续节点就是中间节点* 当n为奇数时,慢指针就是中间节点* 是否是偶数节点看快指针每次是否都能移动两步* -1 -> 1 -> 2 -> 3 -> 4 -> 5 -> null* -1 -> 1 -> 2 -> 3 -> 4 -> null* */if(head == null){return null;}ListNode dummy = new ListNode(-1);dummy.next=head;ListNode slow=dummy;ListNode fast=dummy;ListNode midNode=null;Boolean isEvent=true;while (fast.next!=null){slow=slow.next;if(fast.next.next!=null) {fast = fast.next.next;} else{fast=fast.next;isEvent=false;}}midNode = isEvent ? slow.next : slow;return midNode;}
方法三:双指针优化
解题方法:
定义快慢两个指针,快指针每次移动2步,慢指针每次移动1步
快指针和慢指针都从头节点开始移动
当快指针移动到链尾时,慢指针移动了k步,n>1
当n为偶数时,n-1必然是奇数
即快指针移动了2(k-1)+1步
此时快慢指针距离原点距离
快2(k-1)+1+1 简化 2k
慢k+1
即慢指针正好处于链表中间位置。
当n为奇数时,n-1必然是偶数
,快指针移动了2k步
此时快慢指针距离原点距离
2k+1
k+1
即慢指针正好处于链表中间位置
时间复杂度:O(n)
空间复杂度:O(1)
方法二的本质是下面的公式:
偶数
快2k
慢k
中间k+1
奇数
快2k-1
慢k
中间k
即快慢指针的初始位置+1就把公式统一了。
public ListNode middleNode(ListNode head) {if(head == null){return null;}ListNode slow=head;ListNode fast=head;while (fast!=null && fast.next!=null){slow=slow.next;fast = fast.next.next;}return slow;}
相关文章:

算法系列-876-求链表的中间节点
求链表中间节点,如果有两个中间节点取后面那个 链表定义 // lc codestart /*** Definition for singly-linked list.* public class ListNode {* int val;* ListNode next;* ListNode() {}* ListNode(int val) { this.val val; }* ListNode(…...
h5 ws 客户端 监听ws服务器广播的信息
<!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>AI智能写作</title><!-- Bootstrap CSS --><meta charset"utf-8"><meta name"viewport" content"widt…...
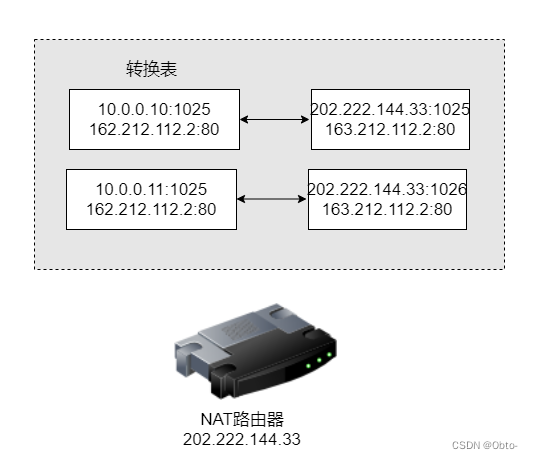
网络基础之重中之重
目录 IP协议 编辑 基本概念: 协议头格式: 编辑 网段划分 DHCP : CIDR: 特殊的IP地址: IP地址的数量限制: 私有IP和公网IP 路由 路由的过程: 数据链路层 认识以太网&#x…...

HarmonyOS应用开发者-----基础认证试题及答案
HarmonyOS应用开发者基础认证试题及答案 试题会不定时刷新,本试题仅供大家学习参考 【判断题】 2.5/2.5 所有使用@Component修饰的自定义组件都支持onPageShow,onBackPress和onPageHide生命周期函数。 正确(True)错误(False) 回答正确【判断题】 2.5/2.5 在Column和Row容器组…...

C++:string并非以0作为结束符,c_str和data的返回却包含结束符0
C语言中使用char数组保存字符串时,是以字符为0或者\0作为字符串的结束符标志的。 所以一个char str[10]的数组只能合法的保存9个字符(因为最后还要加一个结束符)。 #include <cstring> #include <iostream>using namespace std;int main() {char str[10] ="…...

ChatGPT插件的优缺点
虽然西弗吉尼亚大学的研究人员看到了最新的官方ChatGPT插件——名为“代码解释器”( Code Interpreter)的教育应用潜力,但他们也发现,对于使用计算方法处理针对癌症和遗传疾病的定向治疗的生物数据的科学家来说,这款插…...
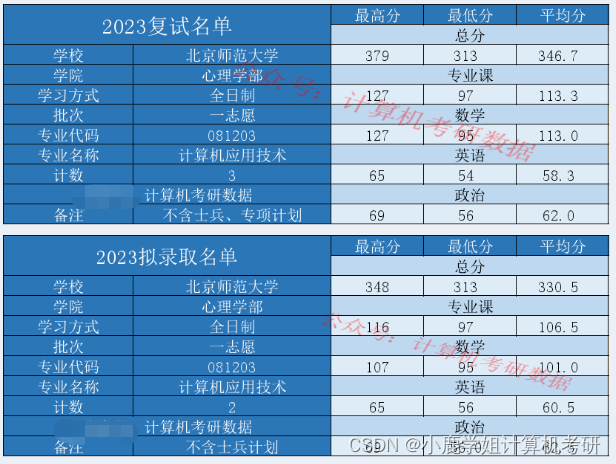
北京985学校,交叉学科考英一数三408
北京师范大学(B) 考研难度(☆☆☆) 内容:23考情概况(拟录取和复试分析)、院校概况、23专业目录、23复试详情、各专业考情分析、各科目考情分析。 正文1096字,预计阅读:3分钟 2023考情概况 北…...
ChatGPT 总结前端HTML, JS, Echarts都包含哪些内容
AIGC ChatGPT ,BI商业智能, 可视化Tableau, PowerBI, FineReport, 数据库Mysql Oracle, Office, Python ,ETL Excel 2021 实操,函数,图表,大屏可视化 案例实战 http://t.csdn.cn/zBytu...

企业架构LNMP学习笔记1
项目开发流程: 公司老板或者产品经理,根据市场调查,决定开发一整套互联网产品。 互动社交电商用户论坛(BBS) 产品决策 (老板产品UI设计) 业务实施、代码开发 程序开发人员 前端开发&#x…...
【位运算】leetcode371:两整数之和
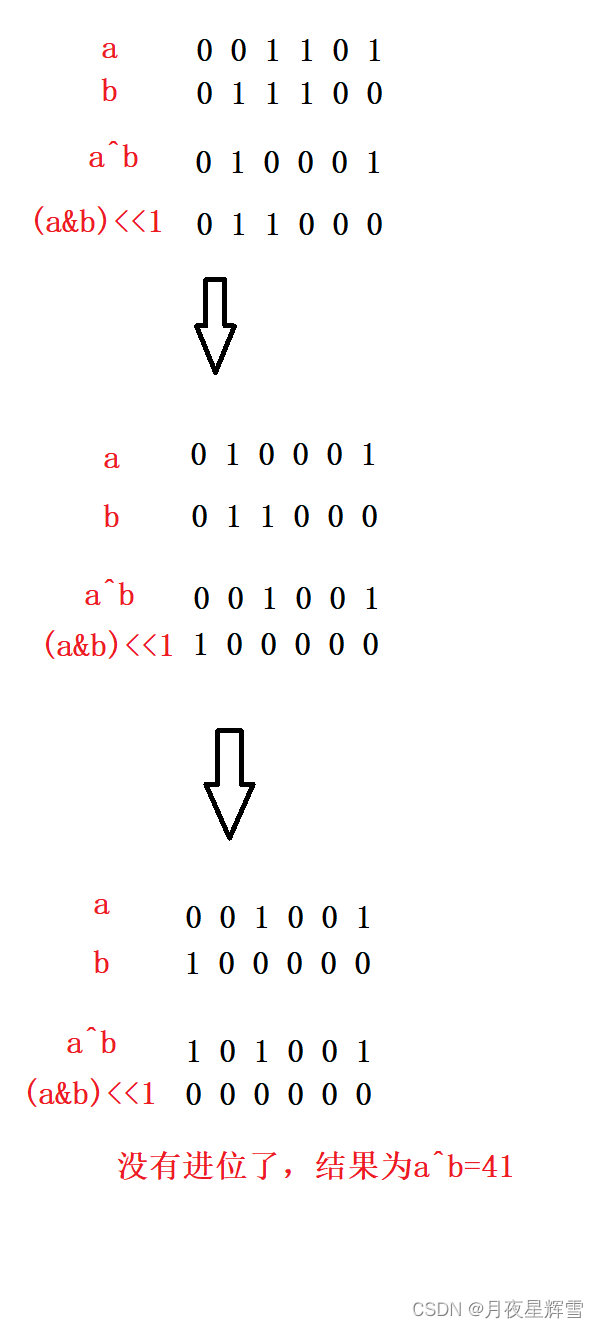
一.题目描述 两整数之和 二.思路分析 题目要求我们实现两整数相加,但是不能使用加号,应该立马想到是用位运算来解决问题。之前说过,异或就是“无进位相加”,故本题可以先将两数异或,然后想办法让得到的结果进位即可。…...

【爬虫小知识】如何利用爬虫爬网页——python爬虫
前言 网络时代的到来,给我们提供了海量的信息资源,但是,想要获取这些信息,手动一个一个网页进行查找,无疑是一项繁琐且效率低下的工作。这时,爬虫技术的出现,为我们提供了一种高效的方式去获取…...
什么是跨域问题 ?Spring MVC 如何解决跨域问题 ?Spring Boot 如何解决跨域问题 ?
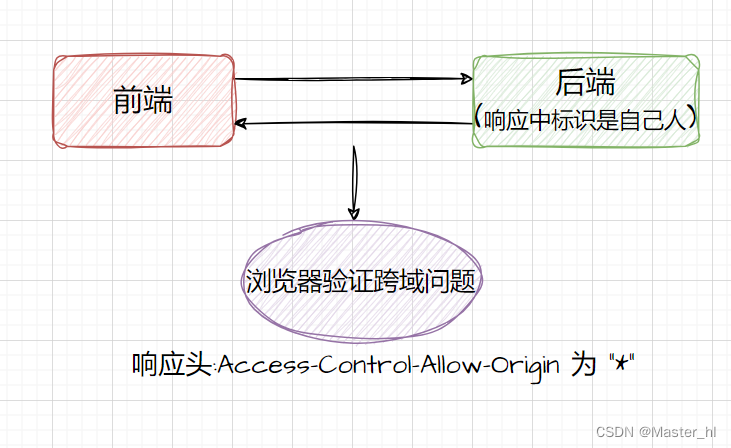
目录 1. 什么是跨域问题 ? 2. Spring MVC 如何解决跨域问题 ? 3. Spring Boot 如何解决跨域问题 ? 1. 什么是跨域问题 ? 跨域问题指的是不同站点之间,使用 ajax 无法相互调用的问题。 跨域问题的 3 种情况&#x…...

线性代数的学习和整理17:向量空间的基,自然基,基变换等(未完成)
目录 3 向量空间的基:矩阵的基础/轴 3.1 从颜色RGB说起 3.2 附属知识 3.3 什么样的向量可以做基? 3.4 基的分类 3.1.1 不同空间的基---向量组的数量可能不同 3.1.2 自然基 3.1.3 正交基 3.1.4 标准正交基 3.1.5 基和向量/矩阵 3.1.6 基变换 …...

Java中支持分库分表的框架/组件/中间件简介
文章目录 1 sharding-jdbc2 TSharding3 Atlas4 Cobar5 MyCAT6 TDDL7 Vitess 列举一些比较常见的,简单介绍一下: sharding-jdbc(当当) TSharding(蘑菇街) Atlas(奇虎360) Cobar&#…...
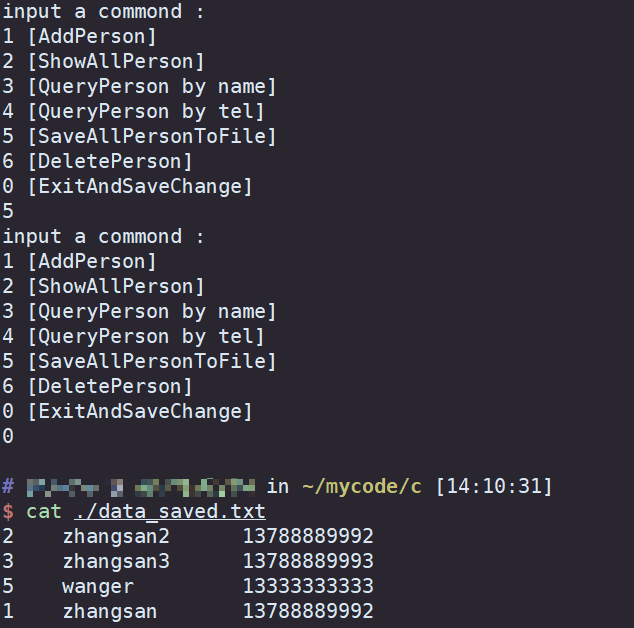
7.2 项目2 学生通讯录管理:文本文件增删改查(C 版本)(自顶向下设计+断点调试) (A)
C自学精简教程 目录(必读) 该作业是 作业 学生通讯录管理:文本文件增删改查(C版本) 的C 语言版本。 具体的作业题目描述,要求,可以参考 学生通讯录管理:文本文件增删改查(C版本)。…...
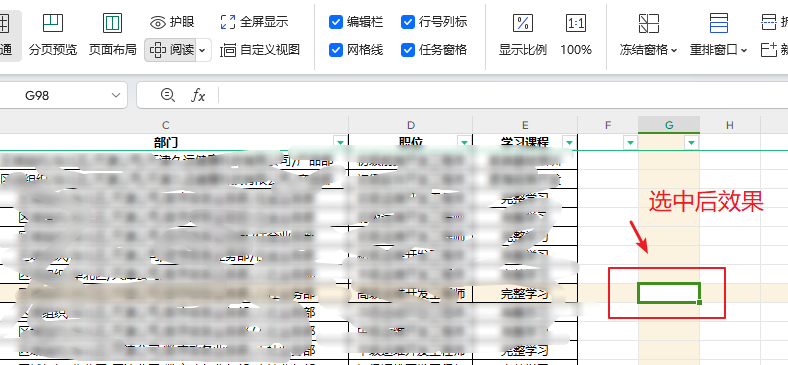
excel怎么设置任意选一个单元格纵横竖横都有颜色
有时excel表格内容过多的时候,我们通过excel设置任意选一个单元格纵横,竖横背景颜色,这样会更加具有辨识度。设置方式截图如下 设置成功后,预览的效果图...

期货-股票交易规则
交易时间 港股:9:00~9:20 集合竞价,9:3012:00,13:0016:00 持续交易,16:00~16:10 随机收市竞价沪股:9:00~9:25 集合竞价,9:3011:30,13:0015:00 持续交易,11:30~12:00 交易申报深股&a…...

Makefile一些语法
ifneq($(filter true,$(xxx)), )的含义 filter 是过滤的意思,它的原型是:$(filter PATTERN…,TEXT), 意义为:过滤掉字串“TEXT”中所有不符合模式“PATTERN”的单词,保留所有符合此模式的单词做返回值。 结合前面的if…...

0基础可以转行编程行业么
在2022年分行业门类分岗位就业人员年平均工资中,信息传输、软件和信息技术服务业的薪资遥遥领先其他行业,为全国平均薪资水平的 1.78 倍,远超第二名金融行业,其年增长率在9.4%,并成为年收入首个过20 万门槛的行业&…...

【spark】dataframe慎用limit
官方:limit通常和order by一起使用,保证结果是确定的 limit 会有两个步骤: LocalLimit ,发生在每个partitionGlobalLimit,发生shuffle,聚合到一个parttion 当提取的n大时,第二步是比较耗时的…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
