100种思维模型之启发式偏差思维模型-017
曾国藩在给儿子的一封家书中曾写道:余于凡事皆用困知勉行工夫,尔不可求名太骤,求效太捷也。熬过此关,便可少进。再进再困,再熬再奋,自有亨通精进之日。
不急躁不求捷径,小火慢炖,将事情做到极致——这是位晚清名臣对儿子的教诲。
我们人做事会走捷径,耍小聪明,其实我们的大脑也经常走捷径。
当大脑在面对一个既复杂模糊又不确定的事件时,往往就会走一些思维的捷径,如,依赖过去的经验,通过对过去的经验进行分析处理,得到启示,然后利用得到的启示作出判断。
思维的捷径,有时能帮助我们快速地做出准确的判断,但有时会导致判断的偏差,查理·芒格对其偏差进行总结,提出“启发式偏差思维模型”。
01、何谓启发式偏差思维模型
一、启发法
人们在日常进行问题解决时或者做抉择时会有两种方式,一种是算法,另一种是启发法。
所谓算法,指的是问题的解决或者抉择能精确的指出每一个步骤;而启发法指的是凭借过往经验去处理问题,当生活中遇到既复杂模糊又不确定的事件时,我们很容易用启发法来做判断。
如,我们来做一道数学题,西瓜和苹果一共1.10元,西瓜比苹果贵1元,请问苹果多少钱?
A. 0.1元;B.1 元;C. 其他。
看到题目,脑海里是不是不怎么思索立马会想到一个数字,0.1元?选A!
对不起,你答错了!正确答案是0.05元。
这道简单的数学题为何会如此容易骗你上当?
是因为它会引起我们大脑的习惯性思考,快速反应但却错误的答案。也会有一些人那一瞬间想到了0.1元,但马上深入思考抵制住了这个想法,进而理性的利用算法得出正确的答案。
二、启发式偏差
所谓启发式偏差,指的是当我们大脑面对某些既复杂又不确定的事物时,由于缺乏行之有效的方法,往往会走一些思考的捷径。
简而言之,就是我们大脑平时往往依赖“启发法”来对事物进行决策判断,而该方法得到的结论并不一定是正确的,会导致决策上的偏差。
三、启发性偏差思维模型
所谓启发式偏差思维模型,就是将启发式思维应用到解决问题上。
生活、工作中在遇到重要问题、重大决策时,问自己是否进行充分思考,是否走了启发法捷径,有意反省,规避启发性偏差,从而做出准确的判断。
02、生活中的启发式偏差现象
生活中的启发式偏差,主要有三种,分别是代表性启发偏差、可得性启发偏差、锚定效应。
一、代表性启发偏差
所谓代表性启发,指的是人们在不确定的情况下,会关注一个事物与另一个事物的相似性,以推断第一个事物与第二个事物的类似之处,人们假定将来的模式会与过去相似并寻求熟悉的模式来做判断,即人们倾向于根据样本是否代表(或类似)总体来判断其出现的概率。
在很多情况下,代表性启发法则是一种非常有效的方法,能帮助人们迅速地抓住问题的本质推断出结果,但有时也会造成严重的偏差,特别是会忽视事件的基本要素,即无条件概率和样本大小,即称作代表性启发偏差。
如,如果我们在公共汽车上看到一个人鬼鬼祟祟,像个小偷,则我们会认为他就是一个小偷,并提高警惕性。
再比如,人们信奉的“小数规则”,即不管样本容量多小,人们总认为它能反映总体。
如,抛硬币猜正反面游戏,当前五次抛出的硬币都是正面时,大多数人就会认为第六次抛出的硬币更可能是反面,因为人们认为"正正正正反"比"正正正正"更具有一般性。
事实上稍微调动下理性,我们都知道,每次抛硬币,出现正、反面的概率都是50%,且与上一次是正、还是反面毫无关系。
二、可得性启发偏差
所谓可得性启发,指的是一种人们根据某种信息容易在心里想起来的程度来进行判断的方法。
如,大家都见过这张希望工程的宣传图片,相信许多人在看到这张照片以后,都会被深深的感动,可能本来没有打算捐钱的结果也捐一点钱,本来打算只捐50块钱的结果捐了100元。

这张图片,让我们对贫困失学儿童有了更为直观的、生动的认识。
这就是所谓的一张图片胜过千言万语。我们的行为很容易因此受到影响——如多捐一些钱。
再比如,当你问别人坐火车和乘飞机哪个更安全,几乎所有的人都会告诉你坐火车更安全,飞机出事故概率大。
其实,飞机事故的发生率远远小于火车事故的发生率,然而一旦飞机出事,电视、广播、报纸等传播纷纷发布重头消息,人们看见、听见了许多有关信息。
所以,当人们比较两种交通工具的安全性时,他们很容易想起关于飞机出事故的报道,因而回答说坐火车更安全。
三、锚定效应
所谓锚定效应,是指当人们需要对某个事件做定量估测时,会将某些特定数值作为起始值,起始值像锚一样制约着估测值。在做决策的时候,会不自觉地给予最初获得的信息过多的重视。
如,有两家卖粥的小店,一家的服务员总是问进来喝粥的顾客:“加不加鸡蛋? ”而另一家的服务员总是问进来喝粥的顾客:“加一个鸡蛋,还是加两个?”。
最后,一天下来,后面一家比前面一家多卖出很多个鸡蛋,且几乎每天如此。
再比如,降序排列的价目表。
不知道大家是否注意过,酒吧或餐厅的菜单价格,一般往往都是按照降序排列的。
把最贵的放在前面,这个价格就成为一个起始参照物。
当顾客从上往下浏览价目表的时候,随着价格越来越便宜,会产生一种金钱获得的感受。
03、怎么更好的应用
一、保持空杯心态
古人云:“常存空杯心,不为所知障”。
林语堂说:
“人生在世,幼时认为什么都不懂,大学时以为什么都懂,毕业后才知道什么都不懂,中年又以为什么都懂,到晚年才觉悟一切都不懂。”
人的一生,总要经历四种认知状态:
1.不知道自己不知道,自以为是,以为自己什么都懂;
2.知道自己不知道,开始有敬畏和空杯的心态;
3.知道自己知道,清楚自己的认知范围;
4.不知道自己知道,永远保持空杯心态。
空杯心态,才是认知的最高境界。
一代武学宗师李小龙也非常推崇空杯心态,他说:“清空你的杯子,方能再行注满,空无以求全。”
二、努力养成参考、采纳外部意见的决策习惯
虽然比起他人意见,我们更偏向于固执自己的意见,且启发法决策往往潜意识上是相信的,是会有意识忽略客观事实的。
这时候,就需要听取他人的意见,以他人意见作为对自己的一种警醒。
三、坚持学习,不断汲取新的知识
要克服固有知识对自己决策判断时的惰性,就必须构建新的知识作为碰撞,更新和替换。
俗话说:“书中自有黄金屋,书中自有颜如玉”。
当我们读的书越来越多时,我们就慢慢找到了许多问题的解决办法。
04、写在最后
启发式偏差思维模型,一个告诉我们大脑怎么走捷径的思维模型。
现实社会是一个复杂适应性系统。有常规事件、随机事件。
常规性事件有规律可循,容易应对;非常规性事件具有高度不确定性和随机性,并具备偶然性和独特性的特质,很难预测和预防。
我们可以用启发法去快速应对常规事情,而要以更加谨慎的态度去应对未来的不确定,认识到自己大脑的启发式偏差,最大化地规避决策陷阱。
相关文章:

100种思维模型之启发式偏差思维模型-017
曾国藩在给儿子的一封家书中曾写道:余于凡事皆用困知勉行工夫,尔不可求名太骤,求效太捷也。熬过此关,便可少进。再进再困,再熬再奋,自有亨通精进之日。 不急躁不求捷径,小火慢炖,将事…...

微服务 feign远程调用时 显示服务不可用 timed-out and no fallback
目录 第一种: failed and no fallback available 1 服务挂掉了 2 服务没有开启 3 注册中心没注册进去 -> ps: 直接调用的接口 通过网关转发失败 会报503 4 高并发下的服务熔断了 第二种: timed-out and no fallback 2.1 业务场景: A服务一切正常 但是B服务显示timeo…...

第一个Java程序(初识Java)
个人主页:平行线也会相交 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 平行线也会相交 原创 收录于专栏【JavaSE_primary】 文章目录1.Java概述1.1什么是Java1.2Java之父2.0第一个Java程序编译运行.class3.0程序如何跑起来的?3.1J…...
vulnhub LordOfTheRoot_1.0.1
总结:端口敲门,CVE-2015-8660提权, 目录 下载地址 漏洞分析 信息收集 端口敲门 网站分析 方法一 ssh登录提权 方法二 下载地址 LordOfTheRoot_1.0.1.ova (Size: 1.6 GB)Download: http://www.mediafire.com/download/m5tbx0dua05szjm…...

MutationObserver与IntersectionObserver
MutationObserver 出现原因:当我们需要监听元素发生变化时,不借助使元素发生变化的业务动作的情况下,使用无污染方式监听非常困难,为了解决这个问题,MutationObserver诞生! 概述 可以用来监听DOM的任何变化…...

【ESP 保姆级教程】玩转巴法云篇② ——MQTT设备云,MQTT协议下的数据通信
忘记过去,超越自己 ❤️ 博客主页 单片机菜鸟哥,一个野生非专业硬件IOT爱好者 ❤️❤️ 本篇创建记录 2023-02-21 ❤️❤️ 本篇更新记录 2023-02-21 ❤️🎉 欢迎关注 🔎点赞 👍收藏 ⭐️留言📝🙏 此博客均由博主单独编写,不存在任何商业团队运营,如发现错误,请…...
植物大战 仿函数——C++
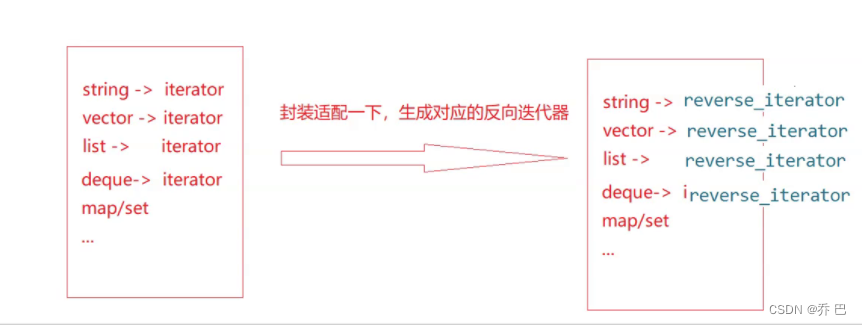
容器适配器 容器适配器不支持迭代器。栈这个东西,让你随便去遍历,是不好的。他是遵循后进先出的。所以他提供了一个街头top取得栈顶数据。 仿函数 仿函数(functor)是C中一种重载了函数调用运算符(operator()&#x…...

【C语言】浮点型数据在内存中的存储
🚀🚀🚀 如果文章对你有帮助不要忘记点赞关注收藏哦🚀🚀🚀 文章目录⭐浮点数在内存中的存储1.1 🤓举个例子:1.2浮点数存储规则🌈:对于M与E有一些特别规定1.3解释前面题目&…...

impala中的刷新元数据和刷新表
impala是Cloudera公司主导开发的新型查询系统,它提供SQL语义,能查询存储在Hadoop的HDFS和HBase中的PB级大数据。 虽然Hive系统也提供了SQL语义,但由于Hive底层执行使用的是MapReduce引擎,仍然是一个批处理过程,难以满…...
Vscode创建vue项目的详细步骤
目录 一、概述 操作的前提 二、操作步骤 一、概述 后端人员想在IDEA里面创建一个Vue的项目,但是这非常麻烦,用vscode这个前端专用软件创建就会非常快速。 操作的前提 1.安装vscode软件的步骤:vscode下载和安装教程和配置中文插件&#…...

如何在面试中介绍自己的项目,才能让软件测试面试官无可挑剔,
四、项目 4.1 简单介绍下最近做过的项目 根据自己的项目整理完成,要点: 1)项目背景、业务、需求、核心业务的流程 2)项目架构,B/S还是C/5,数据库用的什么? 中间件用的什么?后台什么语言开发…...
虹科方案|从 uCPE 到成熟的边缘计算平台
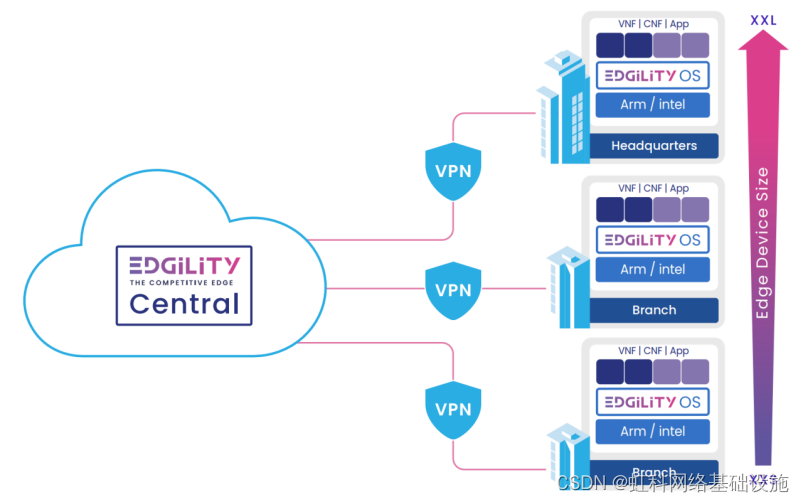
基于开放硬件平台,通用客户端设备 (uCPE) 支持快速添加、集成或删除任意数量的集中管理虚拟功能。 为了增加收入并保持竞争优势,托管服务提供商 (MSP) 和企业正在部署 uCPE 以增强业务敏捷性、加速新服务的引入并提高运营效率。最初,uCPE被部…...
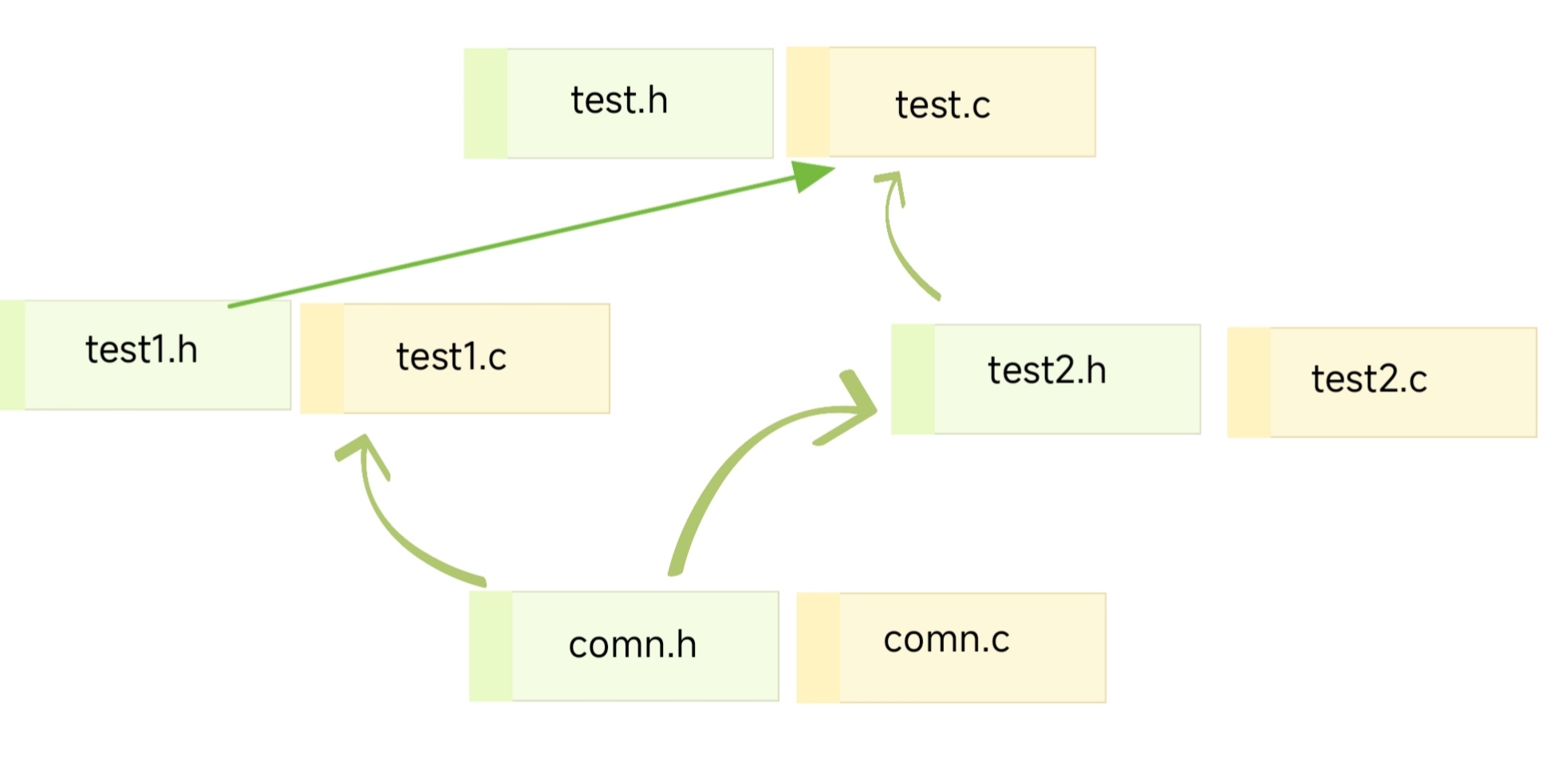
计算机是怎么读懂C语言的?
文章目录前言程序环境翻译环境翻译环境分类编译预处理预处理符号预定义符号#define#undef命令行定义条件编译文件包含头文件包含查找规则嵌套文件包含其他预处理指令编译阶段汇编链接🎉welcome🎉 ✒️博主介绍:博主大一智能制造在读ÿ…...
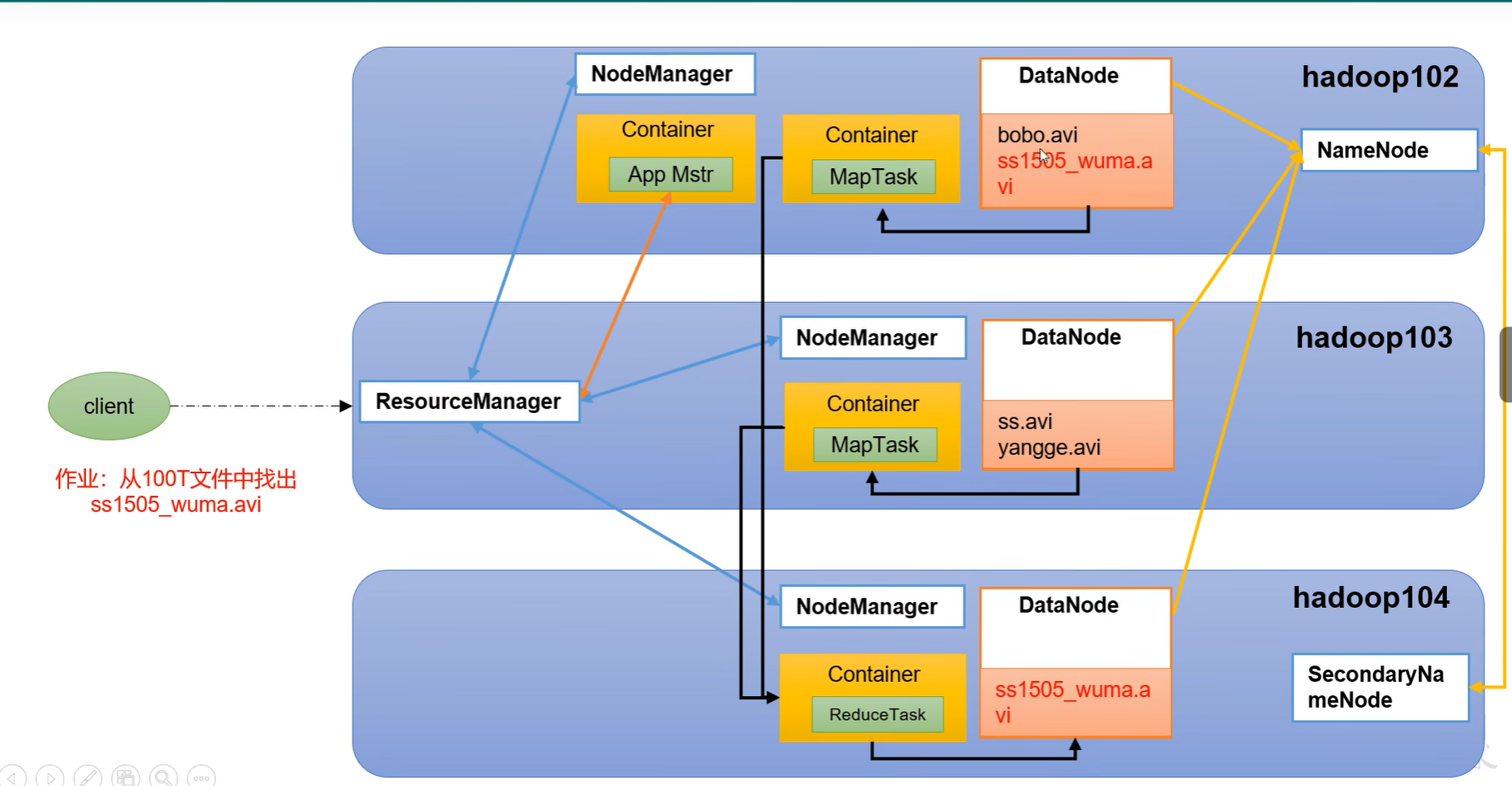
hadoop入门介绍及各组件功能运行关系
文章目录Hadoop 组成部分1.HDFS2.MapReduce 架构概述3. yarn 架构概述4.HDFS、YARN、MapReduce三者关系Hadoop 组成部分 1.HDFS Hadoop Distributed File System,简称 HDFS,是一个分布式文件系统。 HDFS 架构概述 主要分为 NameNode (mn):存储文件的元…...
(HP)新手引导使用react-shepherd
1,官方参数文档:https://shepherdjs.dev/docs/tutorial-02-usage.html 2,基本代码 import { ShepherdTour } from react-shepherd; import ./index.less; // 自己的样式文件,用来修改样式 import ./shepherd.less; // 将shephe…...

数据结构:栈和队列(Leetcode20. 有效的括号+225. 用队列实现栈+232. 用栈实现队列)
目录 一.数据结构--栈 1.栈的基本介绍 2.栈的实现 二.数据结构--队列 1.队列的基本介绍 2.队列的实现 三.栈的运用(Leetcode20. 有效的括号225) 1.问题描述 2.问题分析 题解代码: 四.用两个队列实现栈(225. 用队列实现栈 - 力扣(Leetcode&a…...
)
22.2.19周赛双周赛(贪心、记忆化搜索...)
文章目录双周赛98[6359. 替换一个数字后的最大差值](https://leetcode.cn/problems/maximum-difference-by-remapping-a-digit/)[6361. 修改两个元素的最小分数](https://leetcode.cn/problems/minimum-score-by-changing-two-elements/)贪心排序[6360. 最小无法得到的或值](ht…...
2023最新软件测试面试题(带答案)
1. 请自我介绍一下(需简单清楚的表述自已的基本情况,在这过程中要展现出自信,对工作有激情,上进,好学) 面试官您好,我叫###,今年26岁,来自江西九江,就读专业是电子商务,毕…...
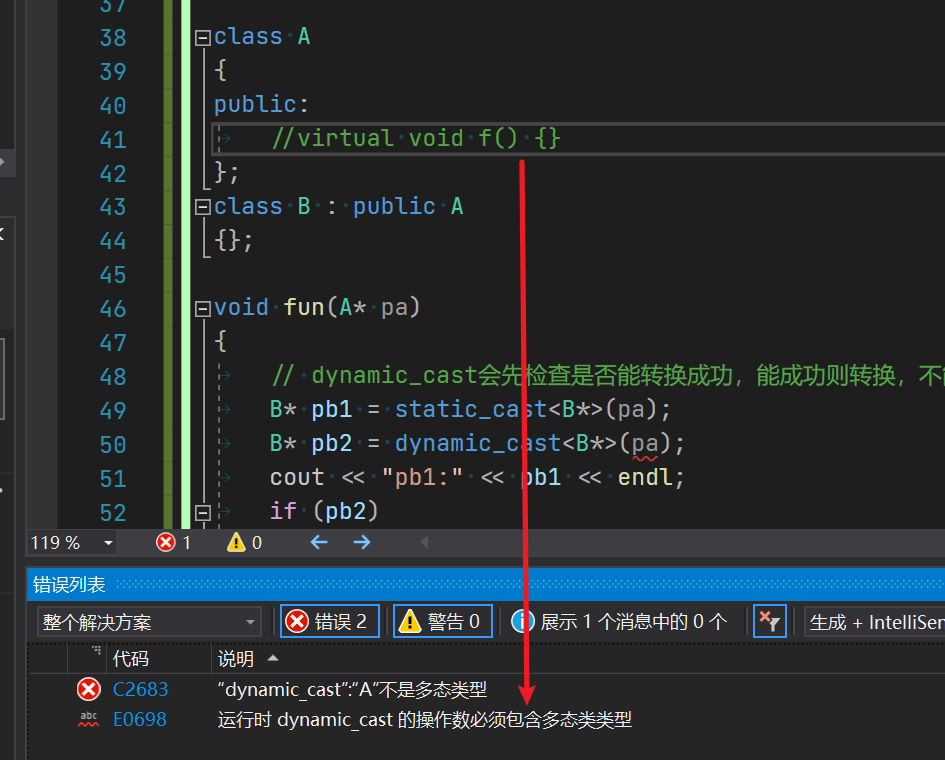
【C++】类型转换方法
本篇博客让我们来见识一下C中新增的类型转换方法 文章目录1.C语言中类型转换2.C中的强制类型转换2.1 static_cast2.2 reinterpret_cast2.3 const_castvolatile关键字2.4 dynamic_cast3.C强制类型转换的作用4.RTTI1.C语言中类型转换 在C语言中,类型转换有下面两种形…...

100亿级订单怎么调度,来一个大厂的极品方案
背景 超时处理,是一个很有技术难度的问题。 所以很多的小伙伴,在写简历的时候,喜欢把这个技术难题写在简历里边, 体现自己高超的技术水平。 在40岁老架构师 尼恩的读者交流群(50)中,尼恩经常指导大家 优化简历。 最…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
