C++--动态规划其他问题
1.一和零 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你一个二进制字符串数组
strs和两个整数m和n。请你找出并返回
strs的最大子集的长度,该子集中 最多 有m个0和n个1。如果
x的所有元素也是y的元素,集合x是集合y的 子集 。示例 1:
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3 输出:4 解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。 其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。示例 2:
输入:strs = ["10", "0", "1"], m = 1, n = 1 输出:2 解释:最大的子集是 {"0", "1"} ,所以答案是 2。
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {int len=strs.size();vector<vector<int>> dp(m+1,vector<int>(n+1));for(int i=1;i<=len;i++){int a=0;int b=0;for(auto sh:strs[i-1]){if(sh=='0') a++;else b++;}for(int j=m;j>=0;j--){for(int k=n;k>=0;k--){dp[j][k]=dp[j][k];if(j>=a&&k-b>=0) dp[j][k]=max(dp[j][k],dp[j-a][k-b]+1);}}}return dp[m][n];}
};2.盈利计划 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
集团里有
n名员工,他们可以完成各种各样的工作创造利润。第
i种工作会产生profit[i]的利润,它要求group[i]名成员共同参与。如果成员参与了其中一项工作,就不能参与另一项工作。工作的任何至少产生
minProfit利润的子集称为 盈利计划 。并且工作的成员总数最多为n。有多少种计划可以选择?因为答案很大,所以 返回结果模
10^9 + 7的值。示例 1:
输入:n = 5, minProfit = 3, group = [2,2], profit = [2,3] 输出:2 解释:至少产生 3 的利润,该集团可以完成工作 0 和工作 1 ,或仅完成工作 1 。 总的来说,有两种计划。示例 2:
输入:n = 10, minProfit = 5, group = [2,3,5], profit = [6,7,8] 输出:7 解释:至少产生 5 的利润,只要完成其中一种工作就行,所以该集团可以完成任何工作。 有 7 种可能的计划:(0),(1),(2),(0,1),(0,2),(1,2),以及 (0,1,2) 。
class Solution {const int MOD = 10 ^ 9 + 7;
public:int profitableSchemes(int n, int m, vector<int>& g, vector<int>& p){int len = g.size();vector<vector<int>> dp(n + 1, vector<int>(m + 1));for (int j = 0; j <= n; j++) dp[j][0] = 1;for (int i = 1; i <= len; i++){for (int j = n; j>=g[i-1]; j--){for (int k=m; k >=0; k--){dp[j][k] += dp[j - g[i - 1]][max(0, k - p[i - 1])];dp[j][k]%=1000000007;}}}return dp[n][m];}
};3.组合总和4 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你一个由 不同 整数组成的数组
nums,和一个目标整数target。请你从nums中找出并返回总和为target的元素组合的个数。题目数据保证答案符合 32 位整数范围。
示例 1:
输入:nums = [1,2,3], target = 4 输出:7 解释: 所有可能的组合为: (1, 1, 1, 1) (1, 1, 2) (1, 2, 1) (1, 3) (2, 1, 1) (2, 2) (3, 1) 请注意,顺序不同的序列被视作不同的组合。示例 2:
输入:nums = [9], target = 3 输出:0
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {int n=nums.size();vector<double> dp(target+1);dp[0]=1;//初始化for(int i=1;i<=target;i++){for(int j=0;j<n;j++){if(i-nums[j]>=0)dp[i]+=dp[i-nums[j]];}}return dp[target];}
};4.不同的二叉搜索树 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台
给你一个整数
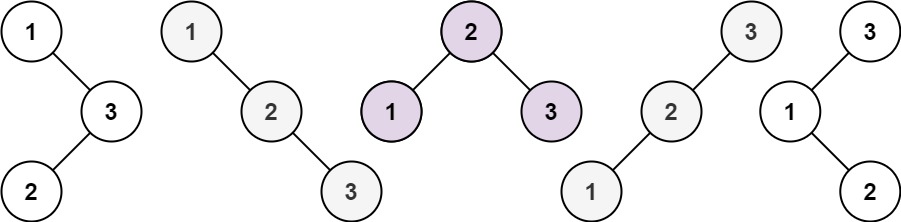
n,求恰由n个节点组成且节点值从1到n互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。示例 1:
输入:n = 3 输出:5示例 2:
输入:n = 1 输出:1
class Solution {
public:int numTrees(int n) {vector<int> dp(n+1);dp[0]=1;for(int i=1;i<=n;i++){for(int j=1;j<=i;j++){dp[i]+=dp[j-1]*dp[i-j];}}return dp[n];}
};相关文章:
C++--动态规划其他问题
1.一和零 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 给你一个二进制字符串数组 strs 和两个整数 m 和 n 。 请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。 如果 x 的所有元素也是 y 的元素࿰…...

PostgreSQL 查询语句大全
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...
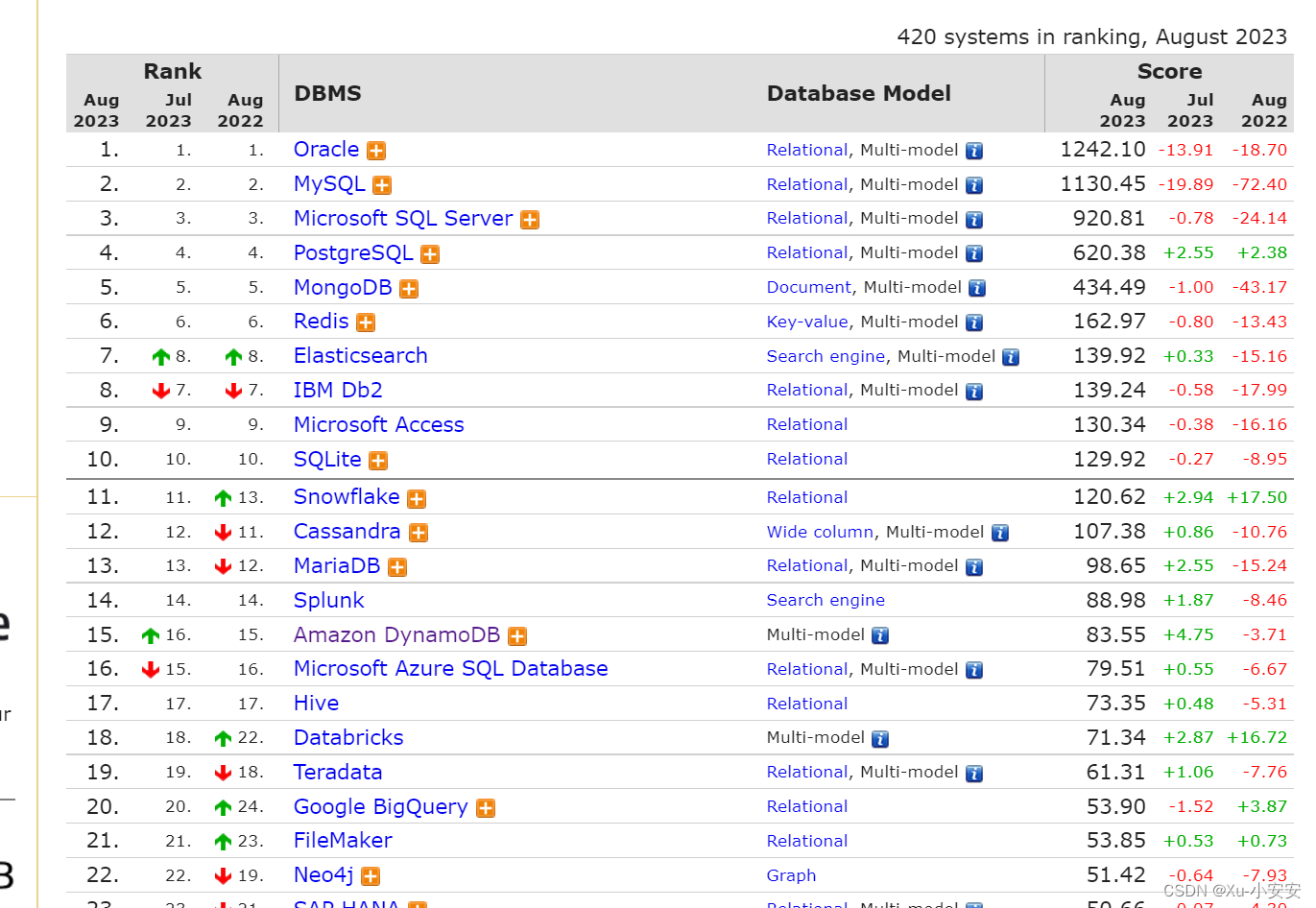
扫盲:常用NoSQL数据库
前言 关系型数据库产品很多,如 MySQL、Oracle、Microsoft SQL Sever 等,但它们的基本模型都是关系型数据模型。 非关系型数据库又称为:NoSQL ,没有统一的模型,而且是非关系型的。 常见的 NoSQL 数据库包括键值数据库、…...

MPI之数据打包和解包
MPI_Pack 和 MPI_Unpack 它们可以将源数据打包成二进制格式以便于传输,或者将二进制格式的数据解包成目标数据。这对函数通常用于在 MPI 应用程序中进行异构系统间的通信,即两个系统之间使用不同的二进制格式进行交互通信。 打包(序列化&…...
9.2作业
QT实现闹钟 widget.h #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include<QTimerEvent> #include<QDateTime> #include<QLineEdit> #include<QLabel> #include<QPushButton> #include <QTextToSpeech> QT_BEGIN_NAMES…...

数据库建设命名规范
1、数据库库表命名规范 1.1 数据库命名规范 采用26个英文字母(区分大小写)和0-9的自然数(经常不需要)加上下划线_组成,命名简洁明确,多个单词用下划线_分隔,一个项目一个数据库,多个项目慎用同一个数据库全部小写命名,禁止出现大…...
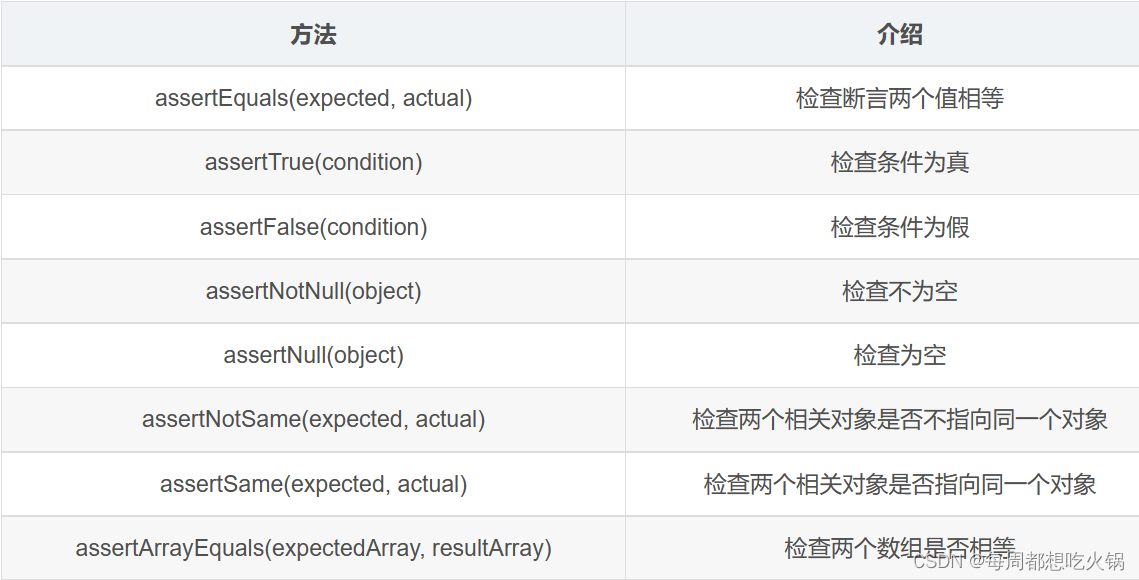
单元测试及其工具Junit
1.单元测试是什么 单元测试是开发者编写的一小段代码,用于检验被测代码的一个很小的、很明确的功能是否正确,通常而言,一个单元测试是用于判断某个特定条件(或者场景)下某个特定函数的行为。 单元测试是软件测试的一种…...

Multicast IP Interface
该模块通过多播IPv4和IPv6在UDP上实现CAN和CAN FD消息的传输。此虚拟接口允许在多个进程甚至主机之间进行通信。这与虚拟接口不同,虚拟接口只能在单个进程中传递消息,但不需要网络堆栈。 它在UDP上运行以具有尽可能低的延迟(与使用TCP相反),并且因为正常的IP多播本质上是…...

从零学算法2833
2833.给你一个长度为 n 的字符串 moves ,该字符串仅由字符 ‘L’、‘R’ 和 ‘’ 组成。字符串表示你在一条原点为 0 的数轴上的若干次移动。 你的初始位置就在原点(0),第 i 次移动过程中,你可以根据对应字符选择移动方…...

python安装cfg模块时报错,ERROR: No matching distribution found for cfg
使用pip3 install cfg2 才行 pip3 install cfg2...

优思学院|六西格玛中的概率分布有哪些?
为什么概率分布重要? 概率分布是统计学中一个重要的概念,它帮助我们理解随机变量的分布情况以及与之相关的概率。在面对具体问题时,了解概率分布可以帮助我们选择适当的检验或分析策略,以解决问题并做出合理的决策。 常见的概率…...
工控上位机程序为什么只能用C语言?
工控上位机程序并不只能用C#开发,实际上在工业自动化领域中,常见的上位机开发语言包括但不限于以下几种:C#: C#是一种常用的编程语言,在工控领域中被广泛使用。它具有良好的面向对象特性和丰富的类库支持,可以实现高性…...
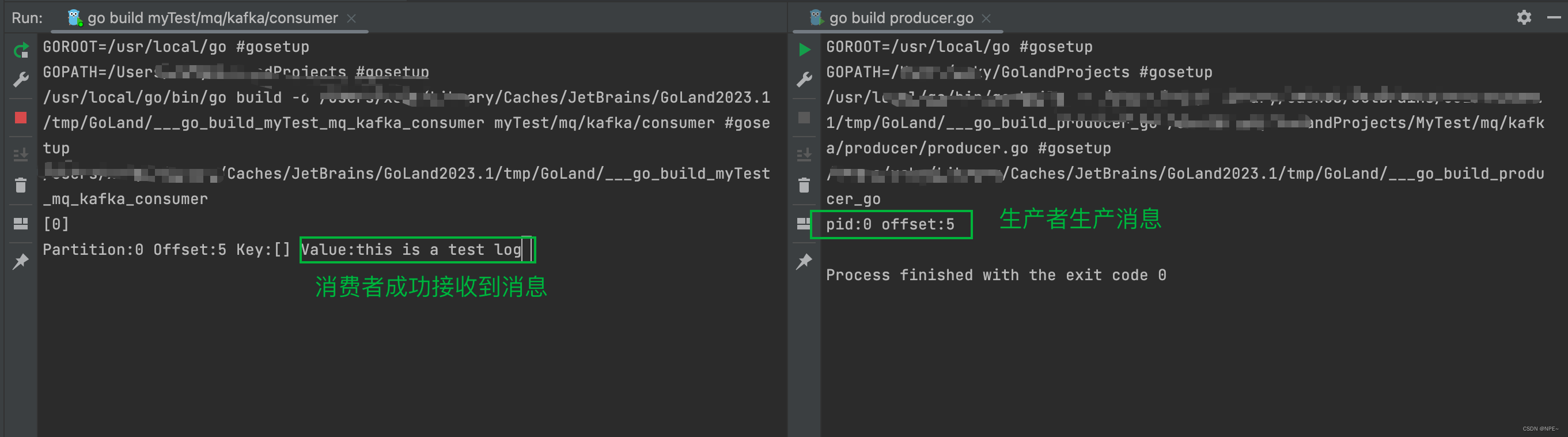
Go操作各大消息队列教程(RabbitMQ、Kafka)
Go操作各大消息队列教程 1 RabbitMQ 1.1 概念 ①基本名词 当前市面上mq的产品很多,比如RabbitMQ、Kafka、ActiveMQ、ZeroMQ和阿里巴巴捐献给Apache的RocketMQ。甚至连redis这种NoSQL都支持MQ的功能。 Broker:表示消息队列服务实体Virtual Host&#x…...

对话出海企业:2023亚马逊云科技出海日圆桌论坛
在全球经济亟待复苏的今天,持续对外开放是中国未来经济发展重要的“两条腿”之一。在愈发饱和的国内市场,中国企业需要对外寻找全新机遇才能在未来不确定的市场博弈下生存下去。“出海”,也成为近几年最炙手可热的词汇之一,大量中…...

【图解算法数据结构】分治算法篇 + Java代码实现
文章目录 一、重建二叉树二、数值的整数次方三、打印从 1 到最大的 n 位数四、二叉搜索树的后序遍历序列五、数组中的逆序对 一、重建二叉树 public class Solution {int[] preorder;HashMap<Integer, Integer> dic new HashMap<>();public TreeNode buildTree(in…...
——Ubuntu开机自动执行命令)
Ubuntu系统环境搭建(八)——Ubuntu开机自动执行命令
ubuntu环境搭建专栏🔗点击跳转 Ubuntu系统环境搭建(八)——Ubuntu开机自动执行命令 修改文件 vim /etc/rc.local以自启动mysql为例,在文件末尾添加 /usr/local/mysql8/bin/mysqld_safe --defaults-file/usr/local/etc/my.cnf …...
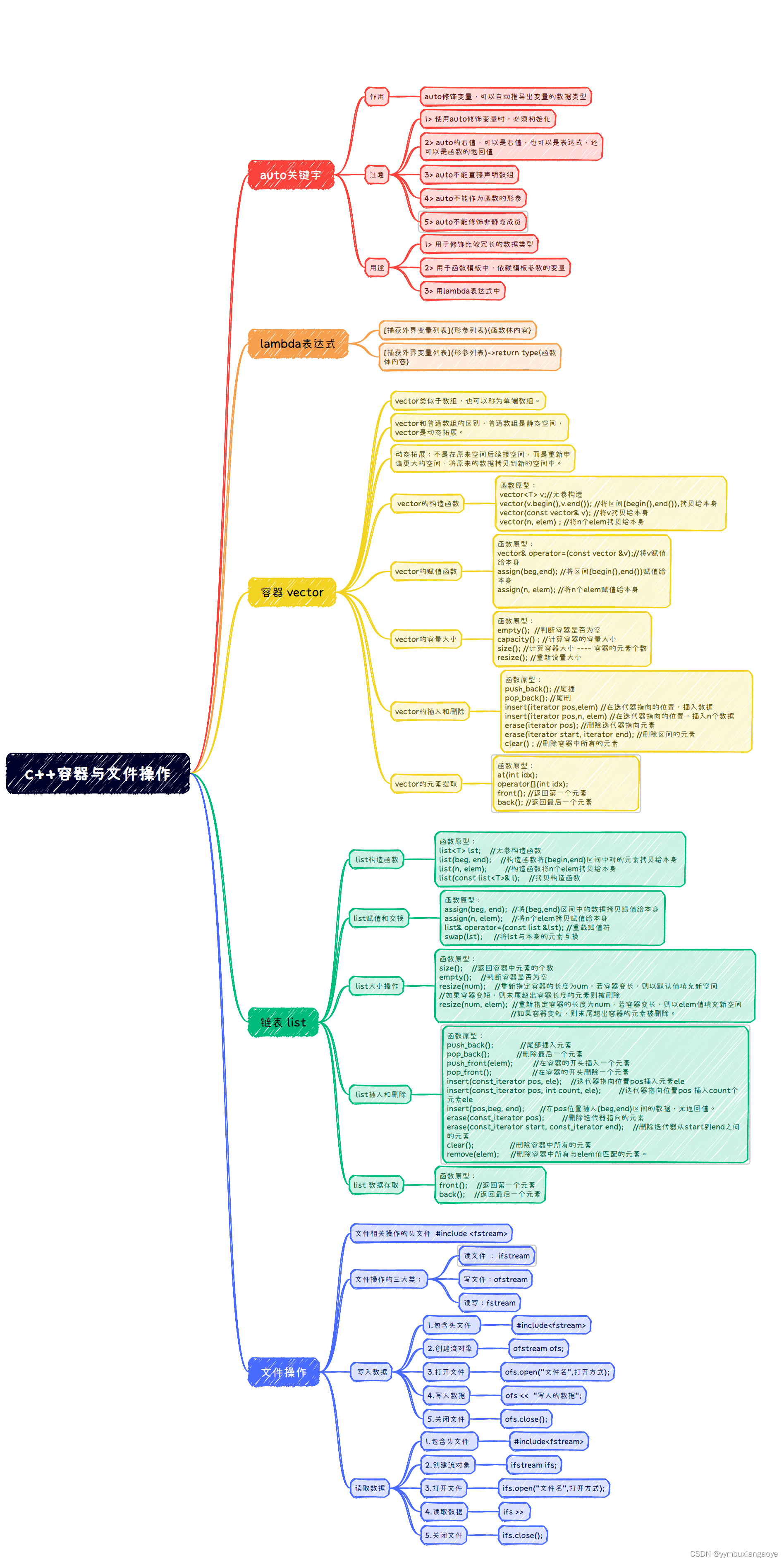
c++(8.29)auto关键字,lambda表达式,数据类型转换,标准模板库,list,文件操作+Xmind
作业: 封装一个学生的类,定义一个学生这样类的vector容器, 里面存放学生对象(至少3个) 再把该容器中的对象,保存到文件中。 再把这些学生从文件中读取出来,放入另一个容器中并且遍历输出该容器里的学生。…...
)
Docker学习笔记(持续更新)
Docker学习目录 1.基础1.1 Docker简介1.1.1 Why Docker?1.1.2 Docker理念1.1.3 容器与虚拟机1.1.4 Docker能做什么? 1.2 Docker的基本组成1.2.1 Docker的三要素1.2.2 Docker平台架构 1.基础 1.1 Docker简介 1.1.1 Why Docker? 在个人笔记本…...

无涯教程-Android - 应用组件
应用程序组件是Android应用程序的基本组成部分,这些组件需要在应用程序清单文件 AndroidManifest.xml 注册,该文件描述了应用程序的每个组件以及它们如何交互。 Android应用程序可以使用以下四个主要组件- Sr.NoComponents & 描述1 Activities 它们…...
树与图c++
1.树 前言 本文主要介绍的数据结构之树型结构的相关知识,树型数据结构是面试官面试的时候非常喜欢考的一种数据结构,树形结构的遍历也是大厂笔试非常喜欢设置的考点,这些内容都会在本篇文章中进行详细的介绍,并且还会介绍一些常…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Vite中定义@软链接
在webpack中可以直接通过符号表示src路径,但是vite中默认不可以。 如何实现: vite中提供了resolve.alias:通过别名在指向一个具体的路径 在vite.config.js中 import { join } from pathexport default defineConfig({plugins: [vue()],//…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...

Spring事务传播机制有哪些?
导语: Spring事务传播机制是后端面试中的必考知识点,特别容易出现在“项目细节挖掘”阶段。面试官通过它来判断你是否真正理解事务控制的本质与异常传播机制。本文将从实战与源码角度出发,全面剖析Spring事务传播机制,帮助你答得有…...

性能优化中,多面体模型基本原理
1)多面体编译技术是一种基于多面体模型的程序分析和优化技术,它将程序 中的语句实例、访问关系、依赖关系和调度等信息映射到多维空间中的几何对 象,通过对这些几何对象进行几何操作和线性代数计算来进行程序的分析和优 化。 其中࿰…...
