Swap and Reverse 题解
Swap and Reverse
题面翻译
题目描述
本题共有 t t t 组数据。
给定一个长度为 n n n 的字符串 s s s 和一个整数 k k k, s s s 只包含小写字母,你可以进行若干次操作(可以是零次),具体操作如下:
-
选取一个 i i i( 1 ≤ i ≤ n − 2 1\le i\le n-2 1≤i≤n−2),交换 a i a_i ai 和 a i + 2 a_{i+2} ai+2
-
选取一个 i i i( 1 ≤ i ≤ n − k + 1 1\le i\le n-k+1 1≤i≤n−k+1),翻转区间 s [ i , i + k − 1 ] s_{[i,i+k-1]} s[i,i+k−1]。如果 s = s 1 , s 2 , … , s i − 1 , s i , s i + 1 , … , s i + k − 2 , s i + k − 1 , s i + k , … , s n − 1 , s n s=s_1,s_2,\dots,s_{i-1},s_i,s_{i+1},\dots,s_{i+k-2},s_{i+k-1},s_{i+k},\dots,s_{n-1},s_n s=s1,s2,…,si−1,si,si+1,…,si+k−2,si+k−1,si+k,…,sn−1,sn,可将其改为: s = s 1 , s 2 , … , s i − 1 , s i + k − 1 , s i + k − 2 , … , s i + 1 , s i , s i + k , … , s n − 1 , s n s=s_1,s_2,\dots,s_{i-1},s_{i+k-1},s_{i+k-2},\dots,s_{i+1},s_i,s_{i+k},\dots,s_{n-1},s_n s=s1,s2,…,si−1,si+k−1,si+k−2,…,si+1,si,si+k,…,sn−1,sn
输出经过若干次操作后得到的的按字典顺序排列的最小字符串。
输入格式
第一行包含一个正整数 t t t,具体含义见上。
第二行包含两个正整数 n n n 和 k k k。
接下来一行 包含一个长度为 n n n 的字符串 s s s。
输出格式
对于每个测试用例,在进行若干次操作后输出按字典顺序排列的最小字符串。
数据范围
1 ≤ t ≤ 1 0 4 , 1 ≤ k ≤ n ≤ 1 0 5 1\le t\le10^4,1\le k\le n\le10^5 1≤t≤104,1≤k≤n≤105。
Translate by @Moss_spresd
题目描述
You are given a string $ s $ of length $ n $ consisting of lowercase English letters, and an integer $ k $ . In one step you can perform any one of the two operations below:
- Pick an index $ i $ ( $ 1 \le i \le n - 2 $ ) and swap $ s_{i} $ and $ s_{i+2} $ .
- Pick an index $ i $ ( $ 1 \le i \le n-k+1 $ ) and reverse the order of letters formed by the range $ [i,i+k-1] $ of the string. Formally, if the string currently is equal to $ s_1\ldots s_{i-1}s_is_{i+1}\ldots s_{i+k-2}s_{i+k-1}s_{i+k}\ldots s_{n-1}s_n $ , change it to $ s_1\ldots s_{i-1}s_{i+k-1}s_{i+k-2}\ldots s_{i+1}s_is_{i+k}\ldots s_{n-1}s_n $ .
You can make as many steps as you want (possibly, zero). Your task is to find the lexicographically smallest string you can obtain after some number of steps.
A string $ a $ is lexicographically smaller than a string $ b $ of the same length if and only if the following holds:
- in the first position where $ a $ and $ b $ differ, the string $ a $ has a letter that appears earlier in the alphabet than the corresponding letter in $ b $ .
输入格式
Each test contains multiple test cases. The first line contains the number of test cases $ t $ ( $ 1 \le t \le 10^4 $ ). The description of the test cases follows.
The first line of each test case contains two integers $ n $ and $ k $ ( $ 1 \le k < n \le 10^5 $ ).
The second line of each test case contains the string $ s $ of length $ n $ consisting of lowercase English letters.
It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 10^5 $ .
输出格式
For each test case, print the lexicographically smallest string after doing some (possibly, zero) steps.
样例 #1
样例输入 #1
5
4 2
nima
5 3
panda
9 2
theforces
7 3
amirfar
6 4
rounds
样例输出 #1
aimn
aandp
ceefhorst
aafmirr
dnorsu
提示
In the first test case, we can obtain the string “aimn” using the following operations:
- Reverse the range $ [3,4] $ . The string turns into “niam”.
- Swap $ s_1 $ and $ s_3 $ . The string turns into “ainm”.
- Reverse the range $ [3,4] $ . The string turns into “aimn”.
It can be proven that we cannot obtain any string lexicographically smaller than “aimn”. Therefore, “aimn” is the answer.
In the second test case, we can obtain the string “aandp” using the following operations:
- Swap $ s_3 $ and $ s_5 $ . The string turns into “paadn”.
- Swap $ s_1 $ and $ s_3 $ . The string turns into “aapdn”.
- Swap $ s_3 $ and $ s_5 $ . The string turns into “aandp”.
It can be proven that we cannot obtain any string lexicographically smaller than “aandp”. Therefore, “aandp” is the answer.
题目大意
两种操作后,能得到的字典序排列最小的字符串
解题思路
观察这两种操作
- 交换 a i a_{i} ai 和 $ a_{i+2} $ 可以得出此操作为交换距离为 2 2 2 的位数操作,即偶数位可以互换,
奇数位可以互换。
-
此时我们观察第二种操作,选取一个 i i i( 1 ≤ i ≤ n − k + 1 1\le i\le n-k+1 1≤i≤n−k+1),翻转区间 s [ i , i + k − 1 ] , s_{[i,i+k-1]}, s[i,i+k−1],
s = s 1 , s 2 , s i − 1 , s i , s i + 1 , , ˙ s i + k − 2 , s i + k − 1 , s i + k , … , s n − 1 , s n s=s_1,s_2,s_{i-1},s_i,s_{i+1},\dot,s_{i+k-2},s_{i+k-1},s_{i+k},\dots,s_{n-1},s_n s=s1,s2,si−1,si,si+1,,˙si+k−2,si+k−1,si+k,…,sn−1,sn,
s = s 1 , s 2 , s i − 1 , s i + k − 1 , s i + k − 2 , … , s i + 1 , s i , s i + k , … , s n − 1 , s n s=s_1,s_2,s_{i-1},s_{i+k-1},s_{i+k-2},\dots,s_{i+1},s_i,s_{i+k},\dots,s_{n-1},s_n s=s1,s2,si−1,si+k−1,si+k−2,…,si+1,si,si+k,…,sn−1,sn
- 当 k k k 为偶数的时候,第二种操作就可以交换距离为奇数的字符,那么结合第一
种操作,我们就可以交换偶数与偶数,奇数与奇数,偶数与奇数,奇数与偶数的
字符了,那么我们直接 $sort\left ( \right ) $ 排序即可。
- 当 k k k 为奇数的时候,只能交换距离为偶数的字符,也就是说只能交换奇数与奇
数,偶数与偶数位置的字符了,所以我们分别针对 n n n 的奇偶性分别排序输出即可
#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
int t;
char s[N]; //存储原始字符
char j[N],o[N]; //分别存储奇数与偶数位的字符
int main()
{cin>>t;while(t--){int n=0,k=0;int l=0,u=0; //分别记录偶数与奇数的数量cin>>n>>k>>s;if(k%2==0){sort(s,s+n);cout<<s<<endl;}else {if(n%2==0){for(int i=0;i<n;i++){if((i+1)%2==0)o[l++]=s[i];else j[u++]=s[i];}sort(o,o+l);sort(j,j+u);for(int i=0;i<l;i++) cout<<j[i]<<o[i];cout<<endl;}else {for(int i=0;i<n;i++){if((i+1)%2==0)o[l++]=s[i];else j[u++]=s[i];//奇数}sort(o,o+l);sort(j,j+u);for(int i=0;i<l;i++) cout<<j[i]<<o[i];cout<<j[u-1];cout<<endl;}}}return 0;
}相关文章:

Swap and Reverse 题解
Swap and Reverse 题面翻译 题目描述 本题共有 t t t 组数据。 给定一个长度为 n n n 的字符串 s s s 和一个整数 k k k, s s s 只包含小写字母,你可以进行若干次操作(可以是零次),具体操作如下: 选…...
单元测试:优雅编写Kotlin单元测试
一、MockK简介 MockK是一款功能强大、易于使用的Kotlin mocking框架。在编写单元测试时,MockK能够帮助我们简化代码、提高测试覆盖率,并改善测试的可维护性。除了基本用法外,MockK还提供了许多额外的功能和灵活的用法,让我们能够…...
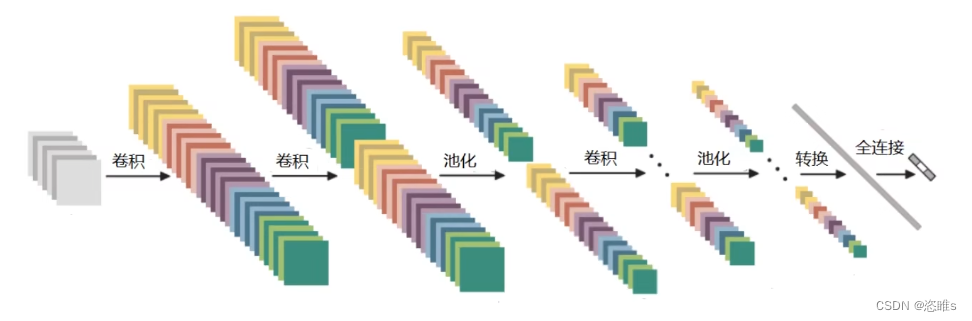
深度学习入门教学——卷积神经网络CNN
目录 一、CNN简介 一、输入层 二、卷积层 三、池化层 四、全连接层 一、CNN简介 1、应用领域 检测任务 分类与检索 超分辨率重构 2、卷积网络与传统网咯的区别 传统神经网络和卷积神经网络都是用来提取特征的。神经网络: 可以将其看作是一个二维的。卷积神经…...
列表(mysqld --verbose --help的结果例))
【MySQL】MySQL系统变量(system variables)列表(mysqld --verbose --help的结果例)
文章目录 【MySQL】MySQL系统变量(system variables)列表(mysqld --verbose --help的结果例)mysqld --verbose --help的结果例参考 【免责声明】文章仅供学习交流,观点代表个人,与任何公司无关。 编辑|SQL和…...
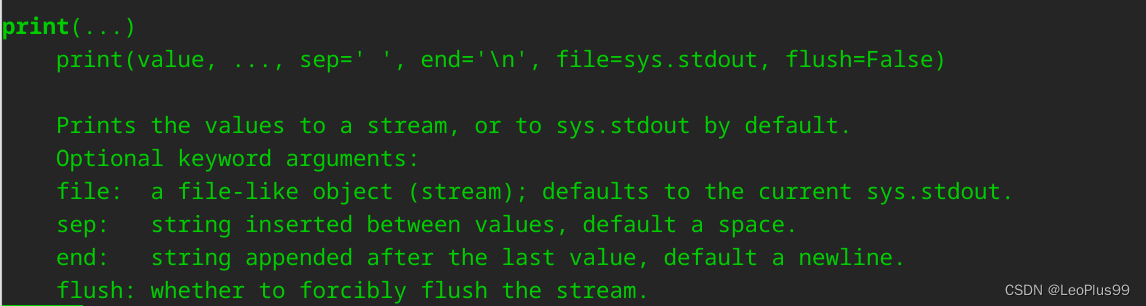
Python学习之四 数据输入与输出
(一) 脚本编程 前面的章节,组要学习了一些简单的Python编程,使用的是交互式解释器,本章节将开始进行脚本编程。可以使用多种编辑器或者IDE完成编码,主要使用vim。 参考前续小节的写法,我们给a、b分别赋值3和5。 在终端运行程序后发现,没有任何输出。这就是本次我们将要…...

VBA技术资料MF51:VBA_在Excel中突出显示唯一值
【分享成果,随喜正能量】世间万物,因果循环不休,你的善心善行,都可能成为你的善缘善果。每天忆佛念佛,每天都在佛菩萨的加持下生活,自然吉祥如意,法喜充满。 。 我给VBA的定义:VBA是…...
Mqtt学习笔记--交叉编译移植(1)
简述 Mqtt目前在物联网行业的应用比较多,mqtt属于应用层的一个中间件,这个中间件实现消息的订阅发布机制。网上介绍Mqtt的实现原来的比较多,这里不细介绍。 其实在我们之前的产品中,自己也开发的有类似的中间件,除了具…...
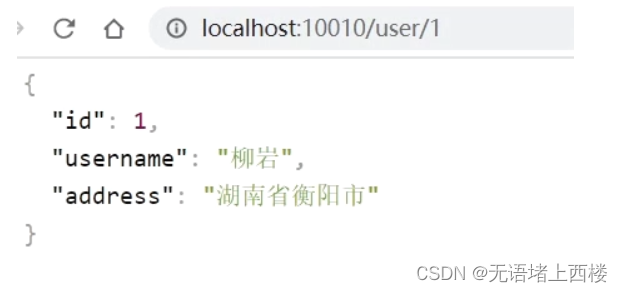
Gateway的服务网关
Gateway服务网关 Gateway网关是我们服务的守门神,所有微服务的统一入口。 网关的核心功能特性: 请求路由 权限控制 限流 架构如下: gateway使用 引入依赖 创建gateway服务,引入依赖 <!--网关--> <dependency>…...

信息化发展18
存储技术 1 、存储分类 2 、常用存储模式的技术与应用对比: ( 1 ) 存储虚拟化( Storage Virtualization ) 是“ 云存储” 的核心技术之一。 它带给人们直接的好处是提高了存储利用率, 降低了存储成本, 简…...
TypeScript学习 + 贪吃蛇项目
TypeSCript简介 TypeScript是JavaScript的超集。它对JS进行了扩展,向JS中引入了类型的概念,并添加了许多新的特性。TS代码需要通过编译器编译为JS,然后再交由JS解析器执行。TS完全兼容JS,换言之,任何的JS代码都可以直…...

YOLO-NAS详细教程-介绍如何进行物体检测
对象检测是计算机视觉中的一项核心任务,可以检测和分类图像中的边界框。自从深度学习首次取得突破以来,它就以极快的速度获得普及和普及,并推动了医疗领域、监控、智能购物等众多公司的发展。考虑到它最终满足了两个基本需求,这一点也就不足为奇了端到端方式:找到所有当前…...

容器没有命令时,如何查看进程、容器executable file not found in $PATH: unknown
前言 当容器没有ps -ef命令时,可以通过以下的命令来查看容器的进程。 docker container top查看容器运行的进程(该命令很有用) #docker container top 命令用于查看容器运行的进程 #当容器里面没有ps -ef命令时,使用docker con…...

如何使用 Amazon EMR 在 Amazon EKS 上构建可靠、高效、用户友好的 Spark 平台
这是 SafeGraph 技术主管经理 Nan Zhu 与亚马逊云科技高级解决方案架构师 Dave Thibault 共同撰写的特约文章。 SafeGraph 是一家地理空间数据公司,管理着全球超过 4100 万个兴趣点(POI,Point of Interest),提供品牌隶…...

国产IDE如何获得捐赠和风险投资
有人在开发VB6 脚本工具,有人在开发VB6的插件,把VB6变成VSCODE界面模式,再加上NUGET,NPM等包管理器原理的在线组件、源码下载功能。 还有TWINBASIC几乎80%代替了VB6,radbasic一直封闭,听说也收到了不少众筹…...

【数学建模】清风数模正课5 相关性分析
相关系数 相关性分析的关键是计算相关系数,在本节课中将会介绍两种常用的相关系数:皮尔逊相关系数(Pearson)和斯皮尔曼相关系数(Spearman)。 它们可以用来衡量两个变量间相关性的大小,对于不同…...

Java设计模式:一、六大设计原则-03:里氏替换原则
文章目录 一、定义:里氏替换原则1.1 里氏替换原则1.2 里氏替换原则的作用 二、模拟场景:里氏替换原则三、违背方案:里氏替换原则3.1 工程结构3.2 储蓄卡和信用卡3.2.1 储蓄卡3.2.2 信用卡 3.3 单元测试3.3.1 储蓄卡测试3.3.2 信用卡测试 四、…...
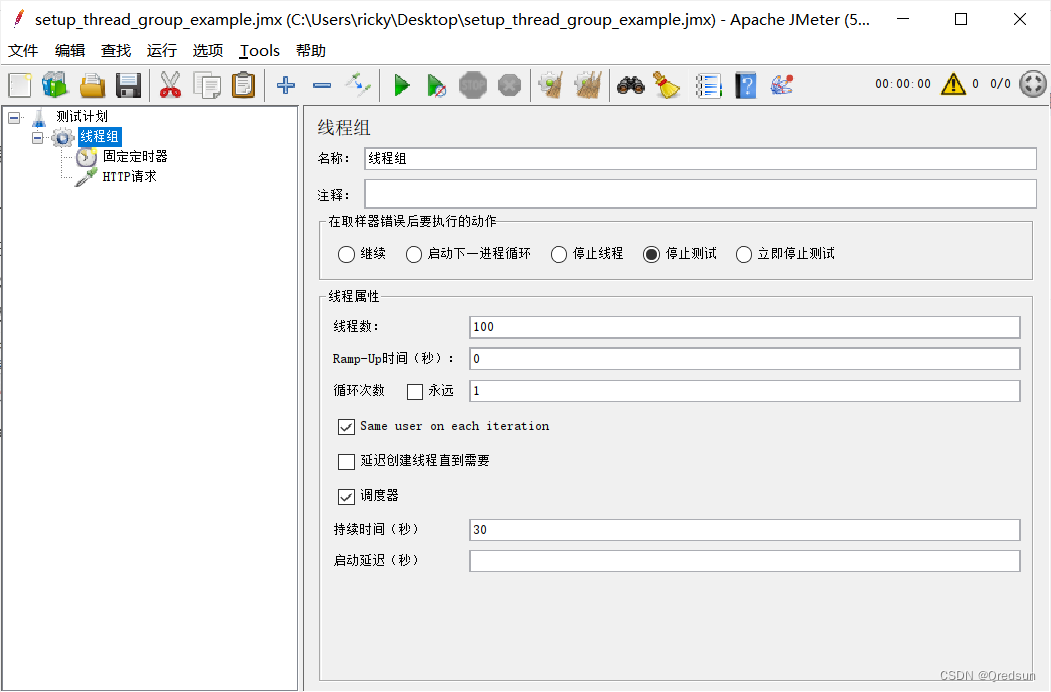
jmeter 固定定时器
固定定时器(Constant Timer)是一个定时器元件,可以在线程组中的每个线程之间添加固定的延迟时间。固定定时器会对每个线程的执行进行一定的暂停。 聊一下和线程组中的调度器对线程组执行时长的影响: 相同: 都会影响线…...
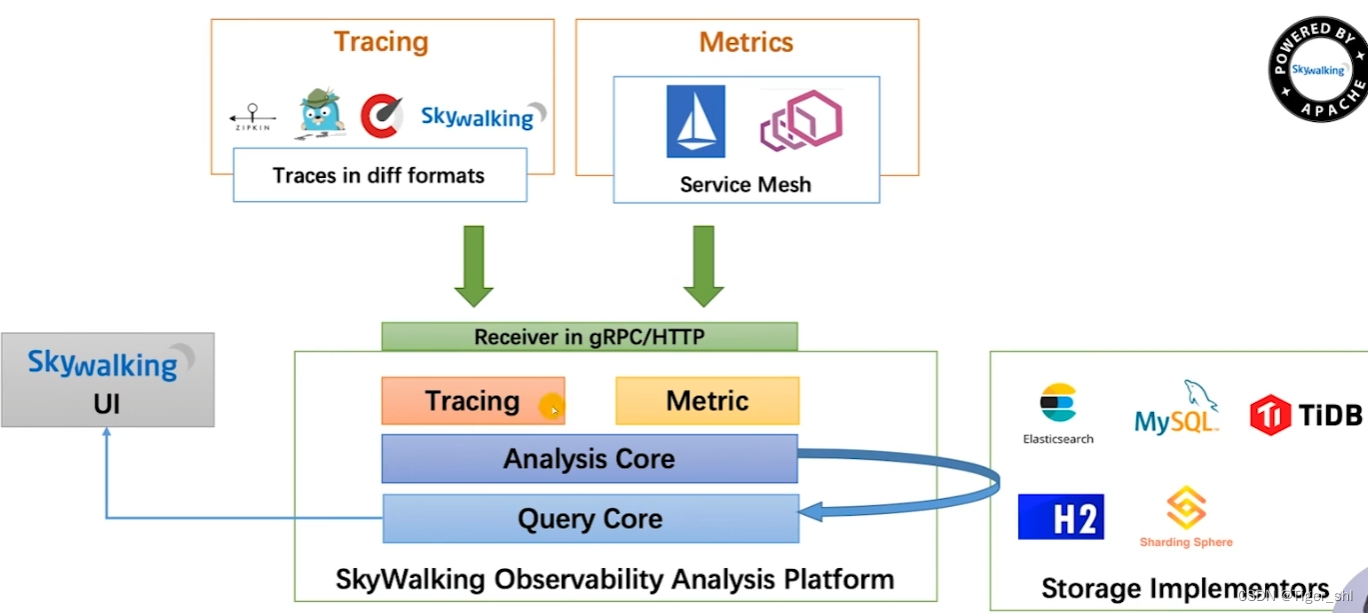
【微服务部署】07-调用链追踪
文章目录 集成SkyWalking实现调用链追踪1. SkyWalking架构图2. 代码集成SkyWalking 集成SkyWalking实现调用链追踪 1. SkyWalking架构图 Receiver是SkyWalking的入口,支持gRPC和HTTP协议。 SkyWalking内部有分析和查询两个部分 存储方面SkyWalking支持Elasticsearc…...

【C++入门】命名空间、缺省参数、函数重载、引用、内联函数
👻内容专栏: C/C编程 🐨本文概括: C入门学习必备语法 🐼本文作者: 阿四啊 🐸发布时间:2023.9.3 前言 C是在C的基础之上,容纳进去了面向对象编程思想,并增加…...

c++ 学习之 构造函数的使用规则
上规则 // 默认情况下,c 编译器至少给一个类添加三个函数 //1.默认构造函数(无参,函数体为空) //2.默认析构函数 (无参 ,函数体为空) //3.默认拷贝函数,对其属性进行值拷贝 //构…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

【Post-process】【VBA】ETABS VBA FrameObj.GetNameList and write to EXCEL
ETABS API实战:导出框架元素数据到Excel 在结构工程师的日常工作中,经常需要从ETABS模型中提取框架元素信息进行后续分析。手动复制粘贴不仅耗时,还容易出错。今天我们来用简单的VBA代码实现自动化导出。 🎯 我们要实现什么? 一键点击,就能将ETABS中所有框架元素的基…...

小智AI+MCP
什么是小智AI和MCP 如果还不清楚的先看往期文章 手搓小智AI聊天机器人 MCP 深度解析:AI 的USB接口 如何使用小智MCP 1.刷支持mcp的小智固件 2.下载官方MCP的示例代码 Github:https://github.com/78/mcp-calculator 安这个步骤执行 其中MCP_ENDPOI…...

React父子组件通信:Props怎么用?如何从父组件向子组件传递数据?
系列回顾: 在上一篇《React核心概念:State是什么?》中,我们学习了如何使用useState让一个组件拥有自己的内部数据(State),并通过一个计数器案例,实现了组件的自我更新。这很棒&#…...

【Vue】scoped+组件通信+props校验
【scoped作用及原理】 【作用】 默认写在组件中style的样式会全局生效, 因此很容易造成多个组件之间的样式冲突问题 故而可以给组件加上scoped 属性, 令样式只作用于当前组件的标签 作用:防止不同vue组件样式污染 【原理】 给组件加上scoped 属性后…...
数据可视化交互
目录 【实验目的】 【实验原理】 【实验环境】 【实验步骤】 一、安装 pyecharts 二、下载数据 三、实验任务 实验 1:AQI 横向对比条形图 代码说明: 运行结果: 实验 2:AQI 等级分布饼图 实验 3:多城市 AQI…...
