数据结构例题代码及其讲解-栈与队列
栈与队列
栈Stack
后进先出
栈的结构体定义及基本操作。
#define MaxSize 50
typedef struct {int data[MaxSize];//栈中存放数据类型为整型int top;//栈顶指针
}Stack;
初始化
这里初始化时是将栈顶指针指向-1,有些则是指向0,因此后续入栈出栈的代码略微有点区别
void InitStack(Stack& S) {//初始化栈S.top = -1;
}
判断栈是否为空
int IsEmpty(Stack S) {//判断栈是否为空if (S.top == -1)return 1;elsereturn 0;
}
压栈操作
- 由于初始时栈顶指针指向-1,因此需要先变化栈顶指针,然后入栈操作;
- 且当MaxSize为50时候,数据域在data[0]~data[49],因此这里是S.top == MaxSize - 1表示栈满;
- 第4-5行可以合并为S.data[++S.top]=x。
int Push(Stack& S, int x) {//压栈操作if (S.top == MaxSize - 1)//若栈满则无法压栈return 0;S.top++;S.data[S.top] = x;return 1;
}
出栈操作
- 这里将出栈的元素用x接收,出栈时先接收,然后栈顶指针自减
- 第4-5行可以合并为x=S.data[++S.top]
int Pop(Stack& S, int& x) {//出栈操作if (S.top == -1)//若栈空则无法出栈return 0;x = S.data[S.top];S.top--;return 1;
}
读取栈顶元素
这里将出栈的元素用x接收
int GetTop(Stack S, int& x) {//读取栈顶元素if (S.top == -1)//若栈空则无栈顶元素return 0;x = S.data[S.top];return 1;
}
当然以上的是顺序栈,还有链栈,和单链表类似,带头结点处为栈头,另外一边为栈底,入栈出栈都在头结点处进行,方便操作。
01 有一个带头结点的单链表 L,结点结构由 data 和 next 两个域构成,其中data 域为字符型。试设计算法判断该链表的全部 n 个字符是否中心对称。例如xyx、xyyx 都是中心对称。
- 判断这类是否中心对称,一般都是用到栈;
- 本题中将其分为前后两部分,把前半部分依次入栈,到后半部分时,与出栈元素进行比较,比较完后栈顶指针移动。遍历指针移动;
- 易错for循环入栈结束后,i所在的位置在栈顶元素的后一个位置,需要i–将其返回到栈顶位置;
- 结点个数为偶数时,正常处理,个数为奇数时,最中间元素不将其压栈处理,让遍历指针再走一步,绕过中间元素;
int central_symmetry(LinkList L, int n) {char S[n / 2];//定义字符型数组来作为一个栈int i;//定义栈顶指针LNode* p = L->next;//定义遍历指针//对称轴左边字符依次入栈for (i = 0; i < n / 2; i++) {S[i] = p->data;p = p->next;}i--;//变量 i 返回栈顶位置if (n % 2 == 1) {//若字符数为奇数则 p 向后遍历一步,因为最中间字符不需考虑p = p->next;}while (p != NULL) {//对称轴右边字符依次与栈顶元素比对if (p->data == S[i]) {//与栈顶元素相等则 p 继续遍历与下一出栈元素比较i--;//出栈p = p->next;//继续遍历}else//若不等,则说明 n 个字符不对称,直接返回 0return 0;//非中心对称}return 1;//若正常跳出循环,则证明 n 个字符对称,返回 1
}
02 假设一个算术表达式中包含小括号和中括号 2 种类型的括号,编写一个算法来判别表达式中的括号是否配对,假设算术表达式存放于字符数组中,以字符‘\0’作为算术表达式的结束符。
- 本题中对于数字和运算符不需要进行操作
- switch语句从上往下依次执行,因此需要break跳出;
- 遇到右括号时候,首先得判断栈是否为空,为空则说明不匹配了;
- 若数组遍历完成后栈为空,则证明所有左括号全部配对成功
int BracketsCheck(char a[]) {Stack S;InitStack(S);char x;for (int i = 0; a[i] != '\0'; i++) {switch (a[i]) {case'('://若数组元素为左括号,则压栈继续遍历push(S, a[i]);break;case'[':push(S, a[i]);break;case')'://若元素为右括号,则需考虑是否有左括号与之配对if (IsEmpty(S) {return 0;//若栈空,则说明无左括号与之配对}else {Pop(S, x);if (x != '(') {//若栈不为空,则判断栈顶元素与当前括号是否配对return 0;}//配对上了break;}case']':if (IsEmpty(S)) {return 0;}else {Pop(S, x);if (x != '[') {return 0;}break;}default://若数组元素不是括号则直接继续遍历break;}}if (IsEmpty(S)) {//若数组遍历完成后栈为空,则证明所有左括号全部配对成功return 1;}else {//若栈不为空,则证明有左括号未配对retun 0;}
}
03 两个栈 S1、S2 都采用顺序栈方式,并共享一个存储区[0,…,MaxSize-1],为了尽量利用空间,减少溢出的可能,可采用栈顶相向、迎面增长的存储方式。试设计写出此栈的定义和 S1、S2 有关入栈和出栈的操作算法。
两个栈,需要两个栈顶指针,这里定义了top数组,一个top[0],一个top[1]
#define MaxSize 50
typedef struct{int data[MaxSize];int top[2];//一个top[0],一个top[1]指针
}DStack;
初始化
void InitDStack(DStack& S) {S.top[0] = -1;//初始化 S1 栈顶指针S.top[1] = MaxSize;//初始化 S2 栈顶指针
}
入栈
- 因为一个存储空间有两个栈,因此需要告诉是对哪个栈进行入栈操作,i就是用来区分哪个栈;
- 这里S[1]表示下面的栈,S[2]表示上面的栈
int push(int i, int x) {if (i < 0 || i>1) {return 0;//若 i 的输入不合法,则无法入栈}if (S.top[1] - S.top[0] == 1) {//若存储空间已满,则无法进行入栈操作return 0;}switch (i) {case 0:// S1 栈顶指针上移后入栈S.top[0]++;S.data[S.top[0]] = x;//S.data[++S.top[0]] = x;break;case 1:// S2 栈顶指针下移后入栈S.top[1]--;S.data[S.top[1]] = x;//S.data[--S.top[1]] = x;break;}return 1;
}
出栈
int pop(int i, int& x) {if (i < 0 || i>1) {return 0;}if (S.top[0] == -1 || S.top[1] == MaxSize) {//空栈return 0;}switch (i) {case 0:x = S.data[S.top[0]];S.top[0]--;//下面的栈往下移//x = S.data[S.top[0]--];break;case 1:x = S.data[S.top[1]];S.top[1]++;//上面的栈顶指针往上移//x = S.data[S.top[1]++];break;}return 1;
}
队列Queue
先进先出
队列的结构体定义及其基本操作。
#define MaxSize 50
typedef struct {int data[MaxSize];//队列中存放数据类型为整型int front, rear;//队首指针和队尾指针
}Queue;
void InitQueue(Queue& Q) {//初始化队列Q.front = 0;Q.rear = 0;
}
int IsEmpty(Queue Q) {//判断队列是否为空if (Q.front == Q.rear)//若队首指针和队尾指针指向同一位置,则队列为空return 1;elsereturn 0;
}
队列的入队和出队
这里队尾指针指向元素的后一个位置,详见入队出队操作
入队争对的是队尾指针,需要判断队满Q.rear == MaxSize
//顺序队列的入队和出队:
//这里队尾指针指向元素的后一个位置
int EnQueue(Queue& Q, int x) {//入队操作if (Q.rear == MaxSize)//若队满,则无法入队return 0;Q.data[Q.rear] = x;//变量 x 入队Q.rear++;//队尾指针后移return 1;//入队成功
}出队争对的是队头指针,需要判断队空Q.front == Q.rear
int DeQueue(Queue& Q, int& x) {//出队操作if (Q.front == Q.rear)//若队空,则无法出队return 0;x = Q.data[Q.front];//变量 x 接收出队元素Q.front++;//队首指针后移return 1;//出队成功
}
循环队列
由于之前Q.front == Q.rear判断队空,若循环,则既有判空,又有存满的意思,因此可以牺牲一个空间,使得Q.front == Q.rear只能用来判空。
判空:Q.front == Q.rear
判满:(Q.rear + 1) % MaxSize == Q.front(rear向后移一个是front的话,说明满了)
队尾指针和队首指针往后移动的时候都需要+1取余
//循环队列的入队和出队:(牺牲一个存储空间)
int EnQueue(Queue& Q, int x) {//入队操作if ((Q.rear + 1) % MaxSize == Q.front)//若队满,则无法入队return 0;Q.data[Q.rear] = x;//变量 x 入队Q.rear = (Q.rear + 1) % MaxSize;//队尾指针后移return 1;//入队成功
}
int DeQueue(Queue& Q, int& x) {//出队操作if (Q.front == Q.rear)//若队空,则无法出队return 0;x = Q.data[Q.front];//变量 x 接收出队元素Q.front = (Q.front + 1) % MaxSize;//队首指针后移return 1;//出队成功
}
04 若希望循环队列中的元素都能得到利用,则需设置一个标志域 tag,并以tag的值为0或1来区分队头指针front和队尾指针rear相同时的队列状态是“空”还是“满”。试编写与此结构相应的入队和出队算法。
- 循环队列中,Q.front == Q.rear在原先是能判断队空和队满,因此上面牺牲一个空间进行特别处理;
- 本题通过设置标志域来判断是队空还是队满;
- 这里需要判断队满的只有入队的时候,因此每次入队后将tag变成1;需要判断队空的只有出队的时候,因此每次出队后将tag变成0;由于队空队满判断都需要进行Q.front == Q.rear的判断,因此因此当队首队尾指针不在同一个地方时候,不会进入这个判断,初始时应该将tag置为0。
- Q.front == Q.rear && Q.tag == 1和Q.front == Q.rear && Q.tag == 0的条件下挺强的,都是需要两个条件同时满足
typedef struct {int data[MaxSize];int front, rear;int tag;
}Queue;
void InitQueue(Queue& Q) {//初始化队列Q.front = 0;Q.rear = 0;Q.tag = 0;
}
int EnQueue(Queue& Q, int x) {if (Q.front == Q.rear && Q.tag == 1) {//若队满,则无法进行入队操作return 0;}Q.data[Q.rear] = x;Q.rear = (Q.rear + 1) % MaxSize;//队尾指针后移Q.tag = 1;//入队后可能会出现队满的情况,所以将 tag 标志域置为 1return 1;
}
int DeQueue(Queue& Q, int& x) {if (Q.front == Q.rear && Q.tag == 0) {return 0;//队空}x = Q.data[Q.front];Q.front = (Q.front + 1) % MaxSize;Q.tag == 0;//出队后可能会出现队空的情况,所以将 tag 标志域置为 0return 1;
}
05 Q 是一个队列,S 是一个空栈,实现将队列中的元素逆置的算法。
- 队列先进先出,栈后进先出,要将队列中元素逆置,因此可以依次将队列的元素出队入栈,当队列为空时,然后出栈入队就实现了逆置。
//Q 是一个队列,S 是一个空栈,实现将队列中的元素逆置的算法。
void Reverse(Queue& Q, Stack& S) {int x;while (!IsEmpty(Q)) {//出队列入栈DeQueue(Q, x);Push(S, x);}while (!IsEmpty(S)) {//出栈入队列Pop(S, x);EnQueue(Q, x);}
}
相关文章:

数据结构例题代码及其讲解-栈与队列
栈与队列 栈Stack 后进先出 栈的结构体定义及基本操作。 #define MaxSize 50 typedef struct {int data[MaxSize];//栈中存放数据类型为整型int top;//栈顶指针 }Stack;初始化 这里初始化时是将栈顶指针指向-1,有些则是指向0,因此后续入栈出栈…...

【Spark】Pyspark RDD
1. RDD算子1.1 文件 <> rdd对象1.2 map、foreach、mapPartitions、foreach Partitions1.3 flatMap 先map再解除嵌套1.4 reduceByKey、reduce、fold 分组聚合1.5 mapValue 二元组value进行map操作1.6 groupBy、groupByKey1.7 filter、distinct 过滤筛选1.8 union 合并1.9 …...
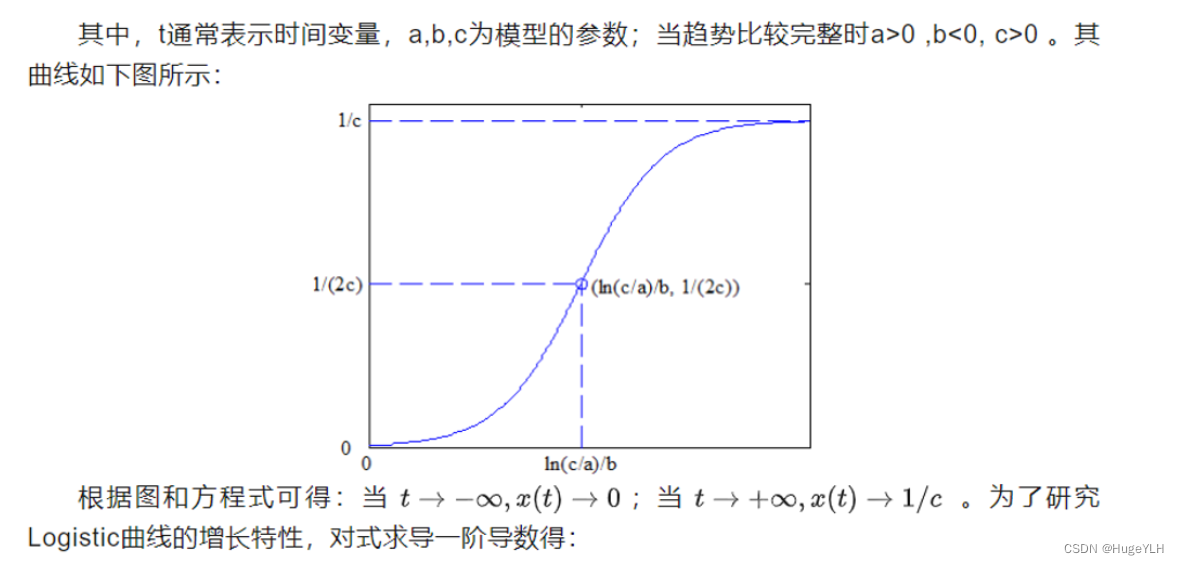
数学建模:Logistic回归预测
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:Logistic回归预测 Logistic回归预测 logistic方程的定义: x t 1 c a e b t x_{t}\frac{1}{cae^{bt}}\quad xtcaebt1 d x d t − a b e b t ( c a e b t ) 2 >…...

一个面向MCU的小型前后台系统
JxOS简介 JxOS面向MCU的小型前后台系统,提供消息、事件等服务,以及软件定时器,低功耗管理,按键,led等常用功能模块。 gitee仓库地址为(复制到浏览器打开): https://gitee.com/jer…...
软件外包开发人员分类
在软件开发中,通常会分为前端开发和后端开发,下面和大家分享软件开发中的前端开发和后端开发分类和各自的职责,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作。 1. 前端开发&…...

HTML 元素被定义为块级元素或内联元素
大多数 HTML 元素被定义为块级元素或内联元素。 10. 块级元素 块级元素在浏览器显示时,通常会以新行来开始(和结束)。 我们已经学习过的块级元素有: <h1>, <p>, <ul>, <table> 等。 值得注意的是: <p> 标签…...

单调递增的数字【贪心算法】
单调递增的数字 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 public class Solution {public int monotoneIncreasingDigits…...
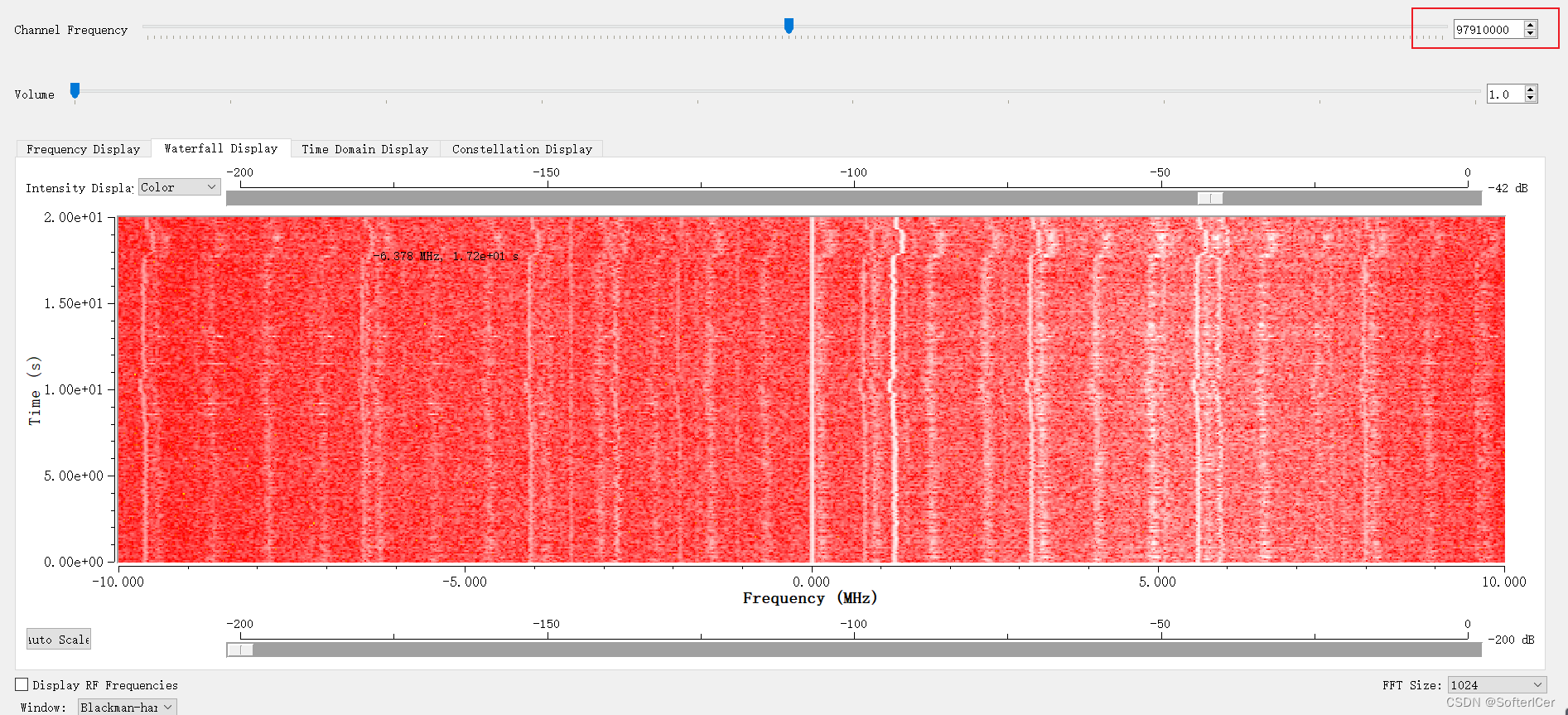
gnuradio-hackrf_info.exe -FM频率使用
97910000...
--生产环境的线程问题诊断)
JVM学习(三)--生产环境的线程问题诊断
1.如何定位哪个进程对cpu占用过高 使用top命令 2.如何定位到某个进程的具体某个线程 使用ps H -eo pid,tid,%cpu | grep 进程id (可以具体定位到某个进程的某个线程的cpu占用情况) 3.如何查看有问题线程的具体信息,定位到代码的行数 使用jstack 进程id 可以找…...

PHP数组处理$arr1转换为$arr2
请编写一段程序将$arr1转换为$arr2 $arr1 array( 0>array (fid>1,tid>1,name>Name1), 1>array (fid>2,tid>2,name>Name2), 2>array (fid>3,tid>5,name>Name3), 3>array (fid>4,tid>7,name>Name4), 4>array (fid>5,tid…...
安全通告 TFV-10 (CVE-2022-47630))
ATF(TF-A)安全通告 TFV-10 (CVE-2022-47630)
安全之安全(security)博客目录导读 ATF(TF-A)安全通告汇总 目录 一、ATF(TF-A)安全通告 TFV-10 (CVE-2022-47630) 二、CVE-2022-47630 2.1 Bug 1:证书校验不足 2.2 Bug 2:auth_nvctr()中缺少边界检查...

详解 SpringMVC 中获取请求参数
文章目录 1、通过ServletAPI获取2、通过控制器方法的形参获取请求参数3、[RequestParam ](/RequestParam )4、[RequestHeader ](/RequestHeader )5、[CookieValue ](/CookieValue )6、通过POJO获取请求参数7、解决获取请求参数的乱码问题总结 在Spring MVC中,获取请…...

Message: ‘chromedriver‘ executable may have wrong permissions.
今天运行项目遇到如下代码 driverwebdriver.Chrome(chrome_driver, chrome_optionsoptions)上述代码运行报错如下: Message: chromedriver executable may have wrong permissions. Please see https://sites.google.com/a/chromium.org/chromedriver/home出错的原…...
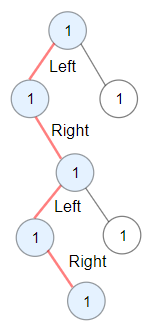
每日一题 1372二叉树中的最长交错路径
题目 给你一棵以 root 为根的二叉树,二叉树中的交错路径定义如下: 选择二叉树中 任意 节点和一个方向(左或者右)。如果前进方向为右,那么移动到当前节点的的右子节点,否则移动到它的左子节点。改变前进方…...

【力扣每日一题】2023.9.2 最多可以摧毁的敌人城堡数量
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题难在阅读理解,题目看得我匪夷所思,错了好多个测试用例才明白题目说的是什么。 我简单翻译一下就是寻找1和…...

kotlin实现java的单例模式
代码 package com.flannery.interviewdemo.singleinstance//https://blog.csdn.net/Jason_Lee155/article/details/128796742 Java实现 //public class SingletonDemo { // private static SingletonDemo instancenew SingletonDemo(); // private SingletonDemo() // …...

使用 KeyValueDiffers 检测Angular 对象的变化
使用 KeyValueDiffers 检测Angular 对象的变化 ngDoCheck钩子 ngDoCheck 是 Angular 生命周期钩子之一。它允许组件在 Angular 检测到变化时执行自定义的变化检测逻辑。 当任何组件或指令的输入属性发生变化、在组件内部发生了变更检测周期或者当主动触发变更检测策略&#…...

Macos 10.13.2安装eclipse
eclipse for php 安装2021-12最后版本4.22 2021-12 R | Eclipse Packages jdk17 x64 dmg安装包,要安装jdk这个才能运行 Java Downloads | Oracle...
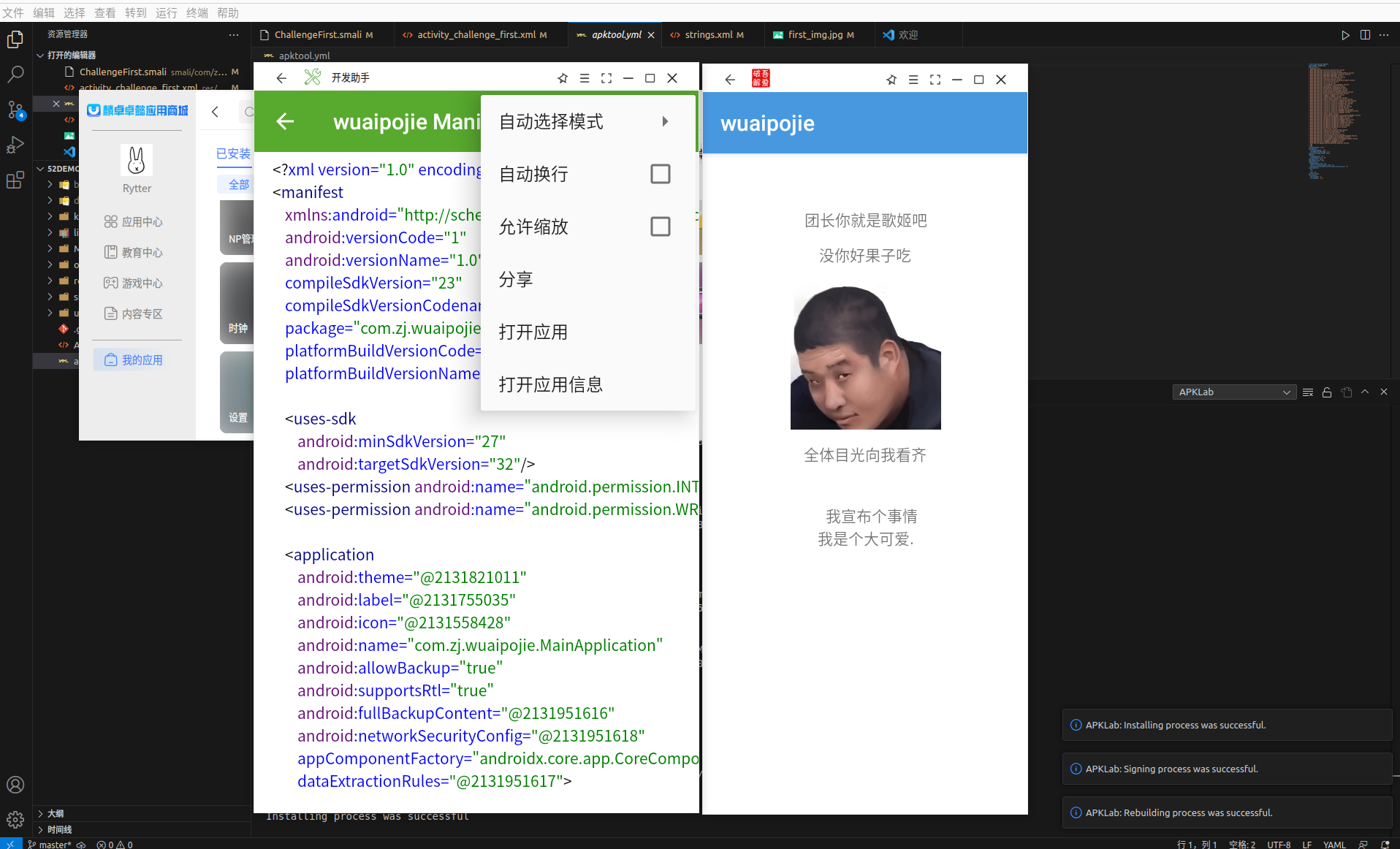
Android逆向学习(一)vscode进行android逆向修改并重新打包
Android逆向学习(一)vscode进行android逆向修改并重新打包 写在前面 其实我不知道这个文章能不能写下去,其实我已经开了很多坑但是都没填上,现在专利也发出去了,就开始填坑了,本坑的主要内容是关于androi…...

【深入浅出设计模式--状态模式】
深入浅出设计模式--状态模式 一、背景二、问题三、解决方案四、 适用场景总结五、后记 一、背景 状态模式是一种行为设计模式,让你能在一个对象的内部状态变化时改变其行为,使其看上去就像改变了自身所属的类一样。其与有限状态机的概念紧密相关&#x…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

NPOI操作EXCEL文件 ——CAD C# 二次开发
缺点:dll.版本容易加载错误。CAD加载插件时,没有加载所有类库。插件运行过程中用到某个类库,会从CAD的安装目录找,找不到就报错了。 【方案2】让CAD在加载过程中把类库加载到内存 【方案3】是发现缺少了哪个库,就用插件程序加载进…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

Chrome 浏览器前端与客户端双向通信实战
Chrome 前端(即页面 JS / Web UI)与客户端(C 后端)的交互机制,是 Chromium 架构中非常核心的一环。下面我将按常见场景,从通道、流程、技术栈几个角度做一套完整的分析,特别适合你这种在分析和改…...

用鸿蒙HarmonyOS5实现中国象棋小游戏的过程
下面是一个基于鸿蒙OS (HarmonyOS) 的中国象棋小游戏的实现代码。这个实现使用Java语言和鸿蒙的Ability框架。 1. 项目结构 /src/main/java/com/example/chinesechess/├── MainAbilitySlice.java // 主界面逻辑├── ChessView.java // 游戏视图和逻辑├──…...
