pytorch异常——loss异常,不断增大,并且loss出现inf
文章目录
- 异常报错
- 异常截图
- 异常代码
- 原因解释
- 修正代码
- 执行结果
异常报错
epoch1:loss3667.782471
epoch2:loss65358620.000000
epoch3:loss14979486720.000000
epoch4:loss1739650891776.000000
epoch5:loss12361745880317952.000000
epoch6:loss2740315398365287284736.000000
epoch7:loss1176857261847129541794856960.000000
epoch8:loss7211548287231028836649926656.000000
epoch9:loss7537356298471407320145204346880.000000
epoch10:lossinf异常截图

异常代码
# 初始化模型的参数,使用正态分布来初始化权重参数,将偏置设置为0
net[0].weight.data.normal_(0,0.01)
net[0].bias.data.fill_(0)# 定义损失函数
loss = nn.MSELoss()# 定义优化算法
trainer = torch.optim.SGD(net.parameters(),lr = 0.03)# 训练
# 训练过程:遍历完整的数据集,每一次都是抽取一个batch_size,然后在进行前向传播计算对应的loss,然后将loss反向传播,计算梯度,然后根据梯度优化参数
num_epochs = 10
for epoch in range(num_epochs):for X,y in data_iter:l = loss(net(X),y)l.backward()trainer.step()l = loss(net(features),labels)print(f'epoch{epoch+1}:loss{l:f}')
原因解释
-
每一个batch_size之后,都没有进行梯度清零,模型参数更新是基于之前所有的mini_batch,并不是基于当前的mini_batch
-
导致如下问题
- 梯度爆炸:如果梯度值在每次迭代中都相对较大,那么累积梯度可能会迅速变得非常大,导致权重更新太过极端。这通常会导致损失值变成 NaN 或 Inf
- 训练不稳定:如果梯度值在每次迭代中都相对较大,那么累积梯度可能会迅速变得非常大,导致权重更新太过极端。这通常会导致损失值变成 NaN 或 Inf
-
梯度下降的基本假设:
- 每次更新都是基于最近一次计算出的梯度,
修正代码
# 初始化模型的参数,使用正态分布来初始化权重参数,将偏置设置为0
net[0].weight.data.normal_(0,0.01)
net[0].bias.data.fill_(0)# 定义损失函数
loss = nn.MSELoss()# 定义优化算法
trainer = torch.optim.SGD(net.parameters(),lr = 0.03)# 训练
# 训练过程:遍历完整的数据集,每一次都是抽取一个batch_size,然后在进行前向传播计算对应的loss,然后将loss反向传播,计算梯度,然后根据梯度优化参数
num_epochs = 10
for epoch in range(num_epochs):for X,y in data_iter:l = loss(net(X),y)trainer.zero_grad()l.backward()trainer.step()l = loss(net(features),labels)print(f'epoch{epoch+1}:loss{l:f}')
执行结果

相关文章:

pytorch异常——loss异常,不断增大,并且loss出现inf
文章目录 异常报错异常截图异常代码原因解释修正代码执行结果 异常报错 epoch1:loss3667.782471 epoch2:loss65358620.000000 epoch3:loss14979486720.000000 epoch4:loss1739650891776.000000 epoch5:loss12361745880317952.000000 epoch6:loss2740315398365287284736.000000…...
Lua学习(一)
lua基础学习 LUA 语言1. 什么是lua?1.1 准备工作 2. 基本语法2.1 注释2.2 标识符2.3 关键字2.4 全局变量 3. 数据类型4. 变量4.1 赋值语句 5. 循环5.1 while循环5.2 for循环5.3泛型for循环5.4 repeat until 循环5.5 break 语句 6. 流程控制6.1 if语句6.2 if else 语…...
Python:列表推导式
相关阅读 Python专栏https://blog.csdn.net/weixin_45791458/category_12403403.html?spm1001.2014.3001.5482 列表推导式使得创建特定列表的方式更简洁。常见的用法为,对序列或可迭代对象中的每个元素应用某种操作,用生成的结果创建新的列表ÿ…...
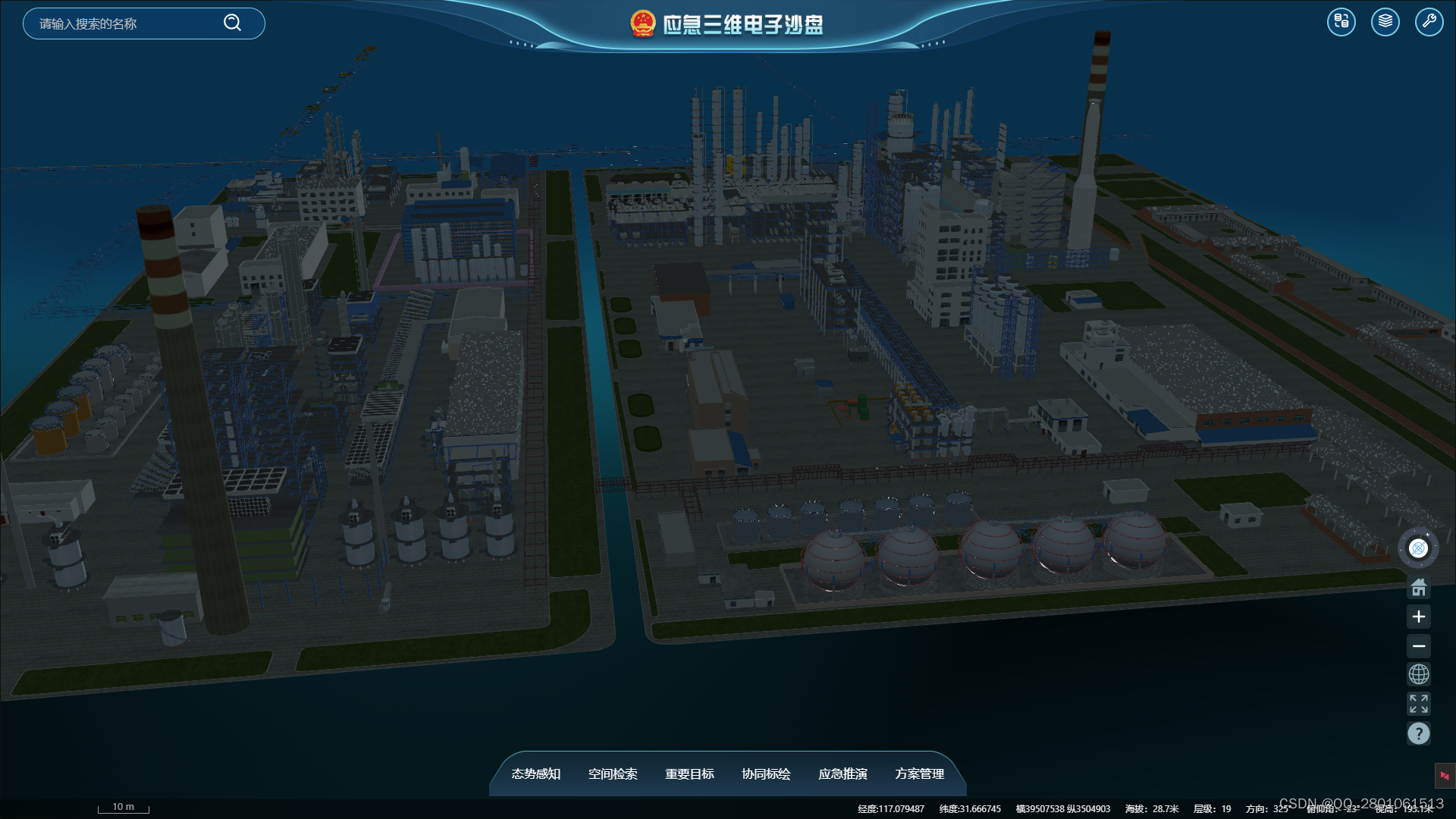
应急三维电子沙盘数字孪生系统
一、简介应急三维电子沙盘数字孪生系统是一种基于虚拟现实技术和数字孪生技术的应急管理工具。它通过将真实世界的地理环境与虚拟世界的模拟环境相结合,实现了对应急场景的模拟、分析和决策支持。该系统主要由三维电子沙盘和数字孪生模型两部分组成。三维电子沙盘是…...
)
LeetCode每日一题:1654. 到家的最少跳跃次数(2023.8.30 C++)
目录 1654. 到家的最少跳跃次数 题目描述: 实现代码与解析: bfs 1654. 到家的最少跳跃次数 题目描述: 有一只跳蚤的家在数轴上的位置 x 处。请你帮助它从位置 0 出发,到达它的家。 跳蚤跳跃的规则如下: 它可以 …...

数据结构例题代码及其讲解-栈与队列
栈与队列 栈Stack 后进先出 栈的结构体定义及基本操作。 #define MaxSize 50 typedef struct {int data[MaxSize];//栈中存放数据类型为整型int top;//栈顶指针 }Stack;初始化 这里初始化时是将栈顶指针指向-1,有些则是指向0,因此后续入栈出栈…...

【Spark】Pyspark RDD
1. RDD算子1.1 文件 <> rdd对象1.2 map、foreach、mapPartitions、foreach Partitions1.3 flatMap 先map再解除嵌套1.4 reduceByKey、reduce、fold 分组聚合1.5 mapValue 二元组value进行map操作1.6 groupBy、groupByKey1.7 filter、distinct 过滤筛选1.8 union 合并1.9 …...
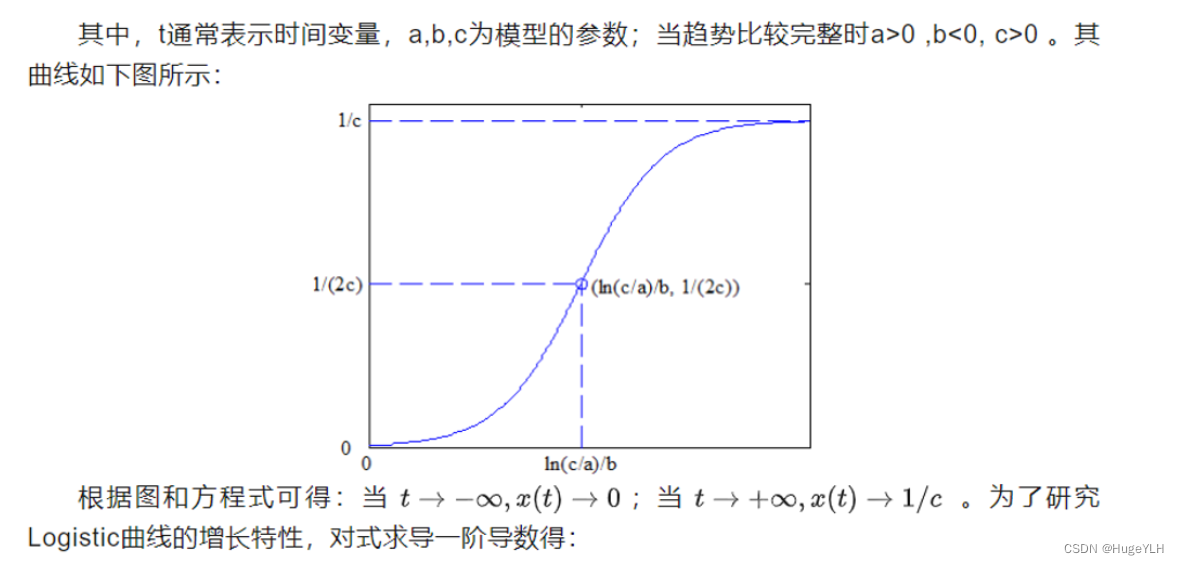
数学建模:Logistic回归预测
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:Logistic回归预测 Logistic回归预测 logistic方程的定义: x t 1 c a e b t x_{t}\frac{1}{cae^{bt}}\quad xtcaebt1 d x d t − a b e b t ( c a e b t ) 2 >…...

一个面向MCU的小型前后台系统
JxOS简介 JxOS面向MCU的小型前后台系统,提供消息、事件等服务,以及软件定时器,低功耗管理,按键,led等常用功能模块。 gitee仓库地址为(复制到浏览器打开): https://gitee.com/jer…...
软件外包开发人员分类
在软件开发中,通常会分为前端开发和后端开发,下面和大家分享软件开发中的前端开发和后端开发分类和各自的职责,希望对大家有所帮助。北京木奇移动技术有限公司,专业的软件外包开发公司,欢迎交流合作。 1. 前端开发&…...

HTML 元素被定义为块级元素或内联元素
大多数 HTML 元素被定义为块级元素或内联元素。 10. 块级元素 块级元素在浏览器显示时,通常会以新行来开始(和结束)。 我们已经学习过的块级元素有: <h1>, <p>, <ul>, <table> 等。 值得注意的是: <p> 标签…...

单调递增的数字【贪心算法】
单调递增的数字 当且仅当每个相邻位数上的数字 x 和 y 满足 x < y 时,我们称这个整数是单调递增的。 给定一个整数 n ,返回 小于或等于 n 的最大数字,且数字呈 单调递增 。 public class Solution {public int monotoneIncreasingDigits…...
gnuradio-hackrf_info.exe -FM频率使用
97910000...
--生产环境的线程问题诊断)
JVM学习(三)--生产环境的线程问题诊断
1.如何定位哪个进程对cpu占用过高 使用top命令 2.如何定位到某个进程的具体某个线程 使用ps H -eo pid,tid,%cpu | grep 进程id (可以具体定位到某个进程的某个线程的cpu占用情况) 3.如何查看有问题线程的具体信息,定位到代码的行数 使用jstack 进程id 可以找…...

PHP数组处理$arr1转换为$arr2
请编写一段程序将$arr1转换为$arr2 $arr1 array( 0>array (fid>1,tid>1,name>Name1), 1>array (fid>2,tid>2,name>Name2), 2>array (fid>3,tid>5,name>Name3), 3>array (fid>4,tid>7,name>Name4), 4>array (fid>5,tid…...
安全通告 TFV-10 (CVE-2022-47630))
ATF(TF-A)安全通告 TFV-10 (CVE-2022-47630)
安全之安全(security)博客目录导读 ATF(TF-A)安全通告汇总 目录 一、ATF(TF-A)安全通告 TFV-10 (CVE-2022-47630) 二、CVE-2022-47630 2.1 Bug 1:证书校验不足 2.2 Bug 2:auth_nvctr()中缺少边界检查...

详解 SpringMVC 中获取请求参数
文章目录 1、通过ServletAPI获取2、通过控制器方法的形参获取请求参数3、[RequestParam ](/RequestParam )4、[RequestHeader ](/RequestHeader )5、[CookieValue ](/CookieValue )6、通过POJO获取请求参数7、解决获取请求参数的乱码问题总结 在Spring MVC中,获取请…...

Message: ‘chromedriver‘ executable may have wrong permissions.
今天运行项目遇到如下代码 driverwebdriver.Chrome(chrome_driver, chrome_optionsoptions)上述代码运行报错如下: Message: chromedriver executable may have wrong permissions. Please see https://sites.google.com/a/chromium.org/chromedriver/home出错的原…...
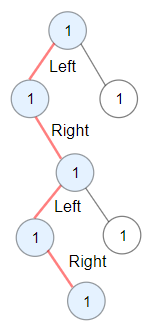
每日一题 1372二叉树中的最长交错路径
题目 给你一棵以 root 为根的二叉树,二叉树中的交错路径定义如下: 选择二叉树中 任意 节点和一个方向(左或者右)。如果前进方向为右,那么移动到当前节点的的右子节点,否则移动到它的左子节点。改变前进方…...

【力扣每日一题】2023.9.2 最多可以摧毁的敌人城堡数量
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题难在阅读理解,题目看得我匪夷所思,错了好多个测试用例才明白题目说的是什么。 我简单翻译一下就是寻找1和…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
