手撕二叉平衡树
今天给大家带来的是平衡树的代码实现,如下:
#pragma once
#include <iostream>
#include <map>
#include <set>
#include <assert.h>
#include <math.h>
using namespace std;
namespace cc
{template<class K, class V>struct AVLnode{int _bf = 0;pair<K, V> _val;AVLnode<K, V>* _left;AVLnode<K, V>* _right;AVLnode<K, V>* _parent;AVLnode(const pair<K, V>& val = pair<K, V>(), AVLnode<K, V>* left = nullptr, AVLnode<K, V>* right = nullptr, AVLnode<K, V>* parent = nullptr): _val(val), _left(left), _right(right), _parent(parent){}};template<class K, class V>class AVL{public:typedef AVLnode<K, V> node;//此parent其实就相当于是旋转点void revolveL(node* parent){//需要改变的节点node* sub = parent->_right;node* subl = sub->_left;//如果根节点是parentif (_root == parent){_root = sub;sub->_parent = nullptr;sub->_left = parent;parent->_parent = sub;parent->_right = subl;if (subl)subl->_parent = parent;}//此旋转点不是根节点else{node* pparent = parent->_parent;if (pparent->_left == parent)pparent->_left = sub;elsepparent->_right = sub;sub->_parent = pparent;sub->_left = parent;parent->_parent = sub;parent->_right = subl;if (subl)subl->_parent = parent;}//旋转完成,更新平衡因子sub->_bf = 0;parent->_bf = 0;}void revolveR(node* parent){node* sub = parent->_left;node* subr = sub->_right;if (_root == parent){_root = sub;sub->_parent = nullptr;sub->_right = parent;parent->_parent = sub;parent->_left = subr;if (subr)subr->_parent = parent;}else{node* pparent = parent->_parent;if (pparent->_left == parent)pparent->_left = sub;elsepparent->_right = sub;sub->_parent = pparent;sub->_right = parent;parent->_parent = sub;parent->_left = subr;if (subr)subr->_parent = parent;}sub->_bf = 0;parent->_bf = 0;}bool insert(const pair<K, V>& x){//根节点为空if (_root == nullptr){_root = new node(x);//节点中父指针已经指向nullptrreturn true;}node* parent = nullptr;node* cur = _root;while (cur){if (x.first < (cur->_val).first){parent = cur;cur = cur->_left;}else if (x.first > (cur->_val).first){parent = cur;cur = cur->_right;}elsereturn false;}cur = new node(x);if ((parent->_val).first > x.first)parent->_left = cur;elseparent->_right = cur;cur->_parent = parent;//插入完成,更新平衡因子while (parent){if (parent->_right == cur)parent->_bf++;else if (parent->_left == cur)parent->_bf--;//此情况说明cur既不是做孩子也不是右孩子,所以直接报错,说明插入的时候出现了问题elseassert(false);if (abs(parent->_bf) == 0)break;else if (abs(parent->_bf) == 1){cur = parent;parent = parent->_parent;}else if (abs(parent->_bf) == 2){//旋转if (parent->_bf == 2 && cur->_bf == 1){revolveL(parent);break;}else if (parent->_bf == -2 && cur->_bf == -1){revolveR(parent);break;}else if (parent->_bf == -2 && cur->_bf == 1){node* sub = parent->_left;node* subr = sub->_right;int bf = subr->_bf;revolveL(sub);revolveR(parent);if (bf == 0){parent->_bf = 0;sub->_bf = 0;subr->_bf = 0;}else if (bf == 1){sub->_bf = -1;parent->_bf = 0;subr->_bf = 0;}else if (bf == -1){sub->_bf = 0;parent->_bf = 1;subr->_bf = 0;}elseassert(false);break;}else if (parent->_bf == 2 && cur->_bf == -1){node* sub = parent->_right;node* subl = sub->_left;int bf = subl->_bf;revolveR(sub);revolveL(parent);subl->_bf = 0;if (bf == 0){// subl->_bf = 0;sub->_bf = 0;parent->_bf = 0;}else if (bf == 1){sub->_bf = 0;// subl->_bf = 0;parent->_bf = -1;}else if (bf == -1){sub->_bf = 1;//subl->_bf = 0;parent->_bf = 0;}elseassert(false);break;}//如果走到这步,说明这棵树的平衡因子有问题elseassert(false);}elseassert(false);}return true;}int high(){return _high(_root);}bool check(){return _check(_root);}private:node* _root = nullptr;bool _check(node* root){if (root == nullptr)return true;int bf = _high(root->_right) - _high(root->_left) ;if (bf != root->_bf){cout << "bf:不一样" << endl;return false;}cout << "bf:" << bf <<" " << "root:" << (root->_val).first << endl;return _check(root->_left) && _check(root->_right);}int _high(node *root){if (root == nullptr)return 0;int left = _high(root->_left);int right = _high(root->_right);if (left > right)return left + 1;elsereturn right + 1;}};
}这个仅仅是平衡树的插入,其实二叉平衡树的插入并不难,逻辑就是那么几个,但是难得是细节处的实现,尤其是平衡因子更新的那一块,特别的容易弄混人,只要记住四种模型就可以了。两种单旋,两种双旋,还是有点难以理解的,下面一一讲解
1.左单旋
左单旋大概的图示这样子的:
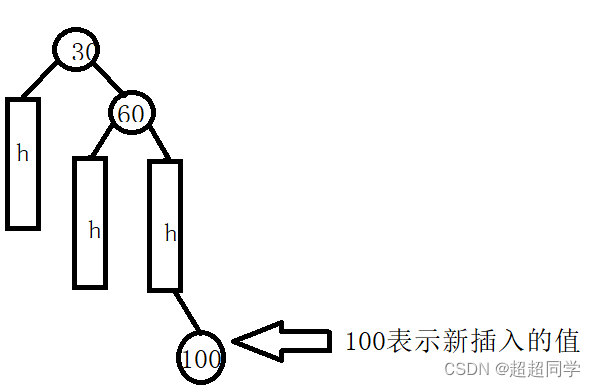
如上图,如果没有插入100,那么此时的二叉平衡树是平衡的,但是此时如果插入100,此时30这个节点的平衡因子是2,所以此时需要旋转来降低这棵树的高度,此时就是左旋。其实此处还分为好几种情况,但是这几种情况都是一样的旋转方法,因为都在60这个节点的右子树中,所以此时就把30当做旋转点,让60左旋,在把60这个节点的左子树链接到30的右指针处就好了。
2.右单旋
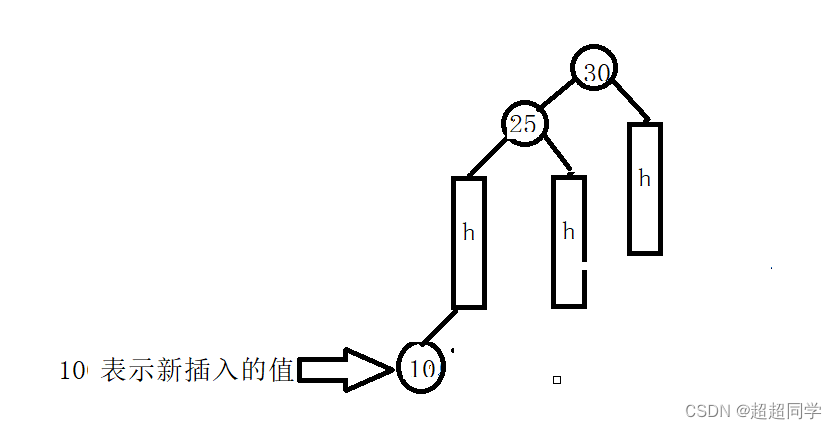
和左单旋一样,因为新插入的节点导致30这个节点的平衡因子为-2,所以此时就要旋转来降低这棵树的高度,此时是要右旋,这个和左旋一样,30是旋转点,25进行右旋,把25这个节点的右子树连接到30这个节点的左子树处就可以了。
3.先左旋,在右旋

这个就是先左旋,在右旋,也是插入了新的节点导致的。这里没有写节点具体的值是因为,因为40这个节点的右子树或是左子树中的值不确定,所以就用了一个空节点来代替插入的值。其实就是两次单旋的结果,先把40以30为旋转点进行左旋,再把60当旋转点进行右旋,此时就旋转完成。而30与40的子树怎么连接参考左单旋与右单旋的旋转方式
4.先右旋,在左旋
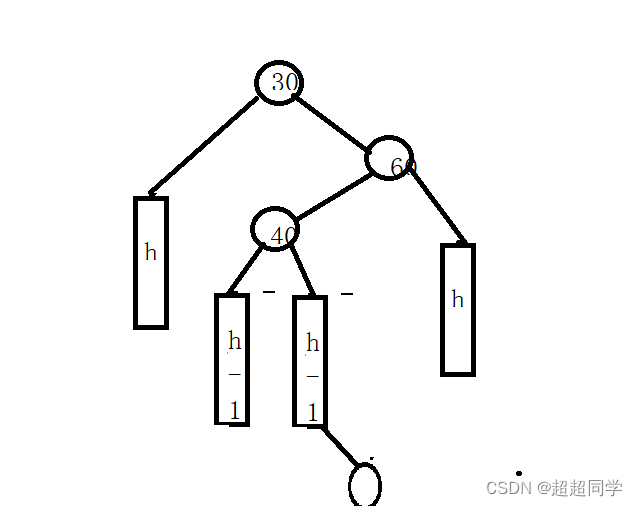
这个模型就是先右旋,在左旋。先把60当旋转点进行旋转,再把30当旋转点进行旋转,至于子树怎么连接,与先左旋,在右旋相同。
以上就是平衡二叉树的旋转方式,下面来总结一下思路:
1.与二叉搜索树的插入一样
2.链接parent指针
3.更新平衡因子
4.如果左右不平衡,那么就开始旋转
增删查时间复杂度:
首先我们知道的是,他是一个二叉树,所以他的高度是log n,而我们在增删查的时候,我们最坏的结果就是要查叶子结点或者所查的节点不在此树,此时它的时间复杂度就是log n,但是他的空间复杂度也是logn,所以个人认为他是以空间换区时间的一种数据结构,但是他的效率确实很高,而对于我们所说的红黑树,其实严格意义来说也是一种logn的算法,但是他没有平衡二叉树这么严谨,平衡二叉树旋转的次数比较多,但是红黑树却没有,旋转其实也是一种消耗,但是旋转的时间复杂度是O(1),严格来说,有消耗,但是也没那么严重,但是对于红黑树来说,就是尽可能不旋转,减少这种消耗。
对于红黑树的代码以及讲解,下一篇会详细讲解,也会对比AVL树和红黑树的优缺点。期待下一篇内容吧!!谢谢大家支持!!!
相关文章:

手撕二叉平衡树
今天给大家带来的是平衡树的代码实现,如下: #pragma once #include <iostream> #include <map> #include <set> #include <assert.h> #include <math.h> using namespace std; namespace cc {template<class K, clas…...
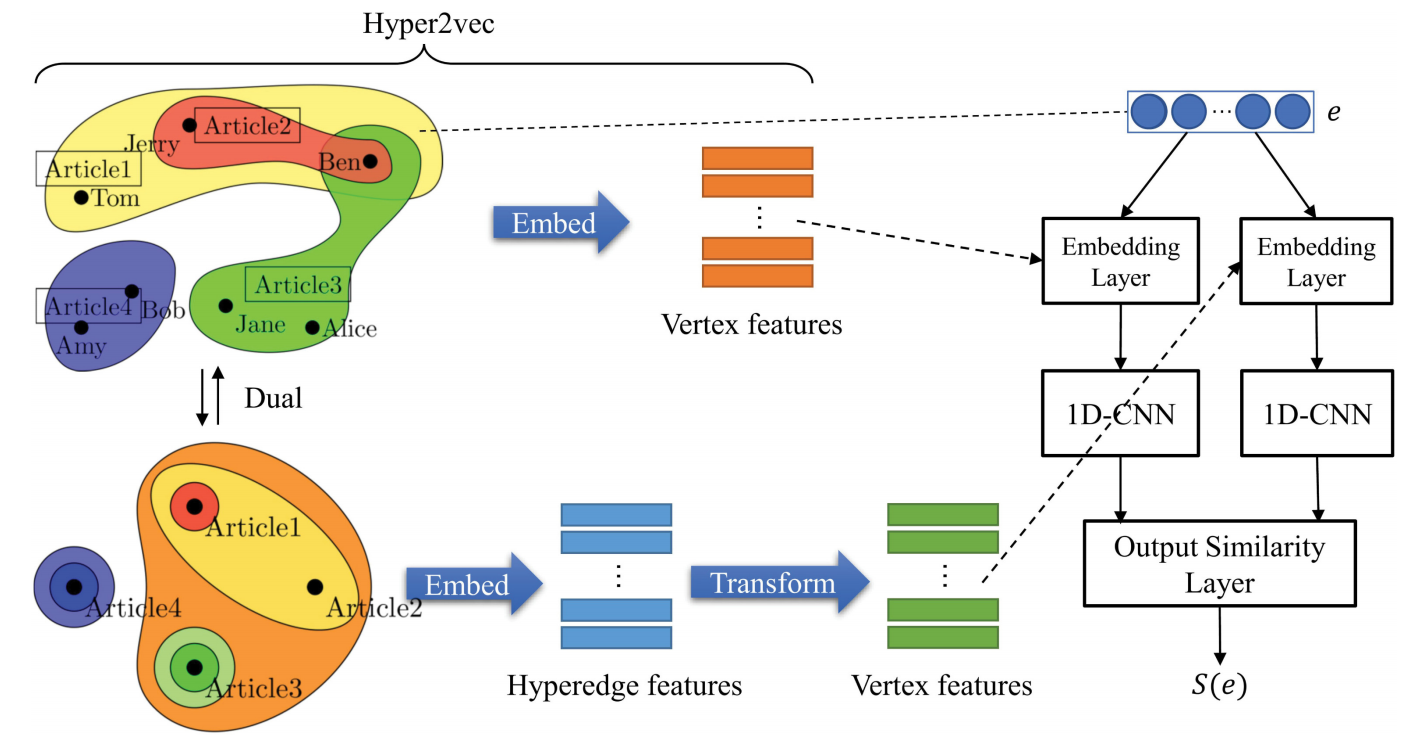
超图嵌入论文阅读1:对偶机制非均匀超网络嵌入
超图嵌入论文阅读1:对偶机制非均匀超网络嵌入 原文:Nonuniform Hyper-Network Embedding with Dual Mechanism ——TOIS(一区 CCF-A) 背景 超边:每条边可以连接不确定数量的顶点 我们关注超网络的两个属性࿱…...
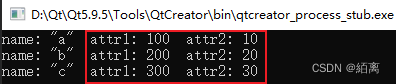
Qt xml解析之QXmlStreamReader
文章目录 背景QXmlStreamReader简单介绍使用QXmlStreamReader添加头文件<QXmlStreamReader>toString()toInt()完整代码 背景 项目中遇到需要解析某个方法返回的xml字符串,奈何C/C中没有原生的方法可供调用,只能使用第三方库,搜了一圈资…...

Selenium基础 — CSS选择器定位大全
1、css属性定位 css选择器策略示例说明#id#telA选择id"telA"的所有元素。.class.telA选择 class"telA”的所有元素。[属性名属性值][nametelA]除了id和class属性,其他属性的定位格式[attribute][target]选择带有target 属性所有元素。**选择所有元素…...

vue3中keep-alive的使用及结合transition使用
正确用法 在组件中使用(这里结合了 transition 内置动画组件 ) <template><div class"layout clearfix"><router-view v-slot"{ Component, route }"><transition name"fade-transform" mode"…...

【提示工程】询问GPT返回Json结构数据
theme: orange 众所周知,我们可以通过构建的Prompt获取期望的内容,但是通常都是以自然语言返回的,假如我们想得到结构化的数据,比如Json,XML那么怎么办,这篇文章给你一个思路。 理所当然的想法 要实现询问大…...

CSS水平垂直居中方案
1 前言 水平居中、垂直居中是前端面试百问不厌的问题。其实现方案也是多种多样,常叫人头昏眼花。 水平方向可以认为是内联方向,垂直方向认为是块级方向。 2 内联元素的水平垂直居中 首先,常见内联元素有:a、span、em、b、stro…...
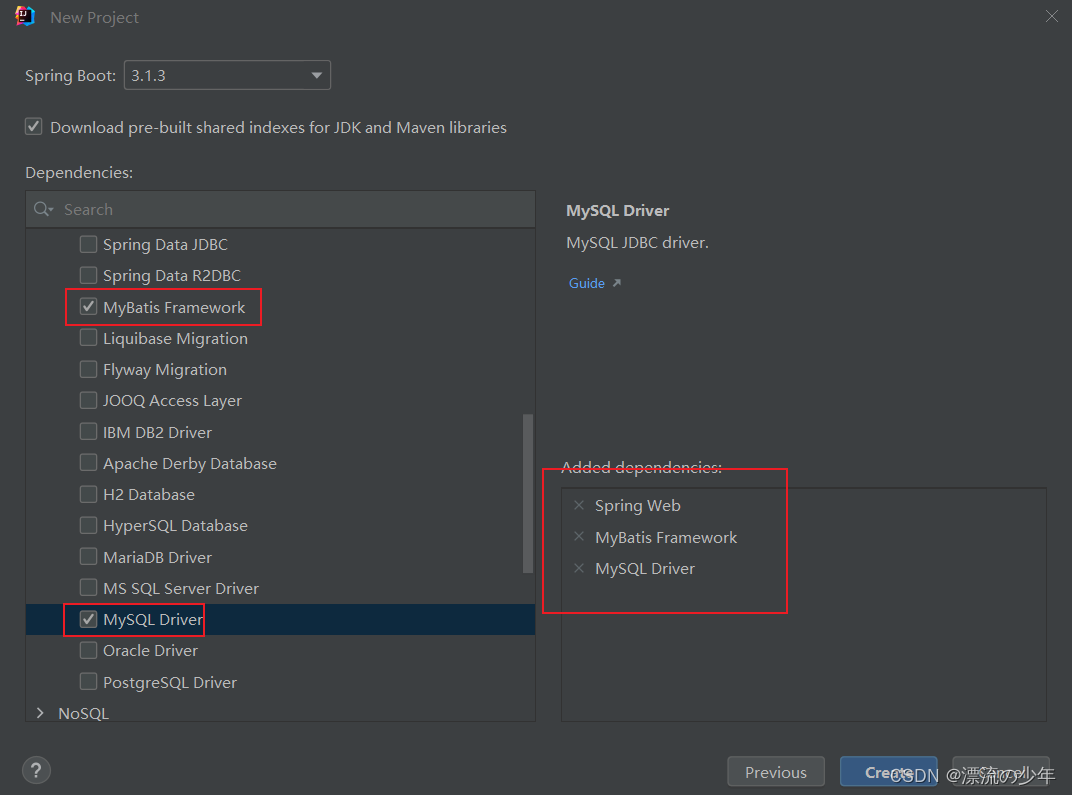
SpringBoot入门篇3 - 整合junit、整合mybatis、基于SpringBoot实现ssm整合
目录 1.整合JUnit Spring整合JUnit SpringBoot整合JUnit 测试类注解:SpringBootTest 作用:设置JUnit加载的SpringBoot启动类 2.整合mybatis ①使用spring initializr初始化项目的时候,添加依赖。 ②设置数据源application.yml spring:d…...
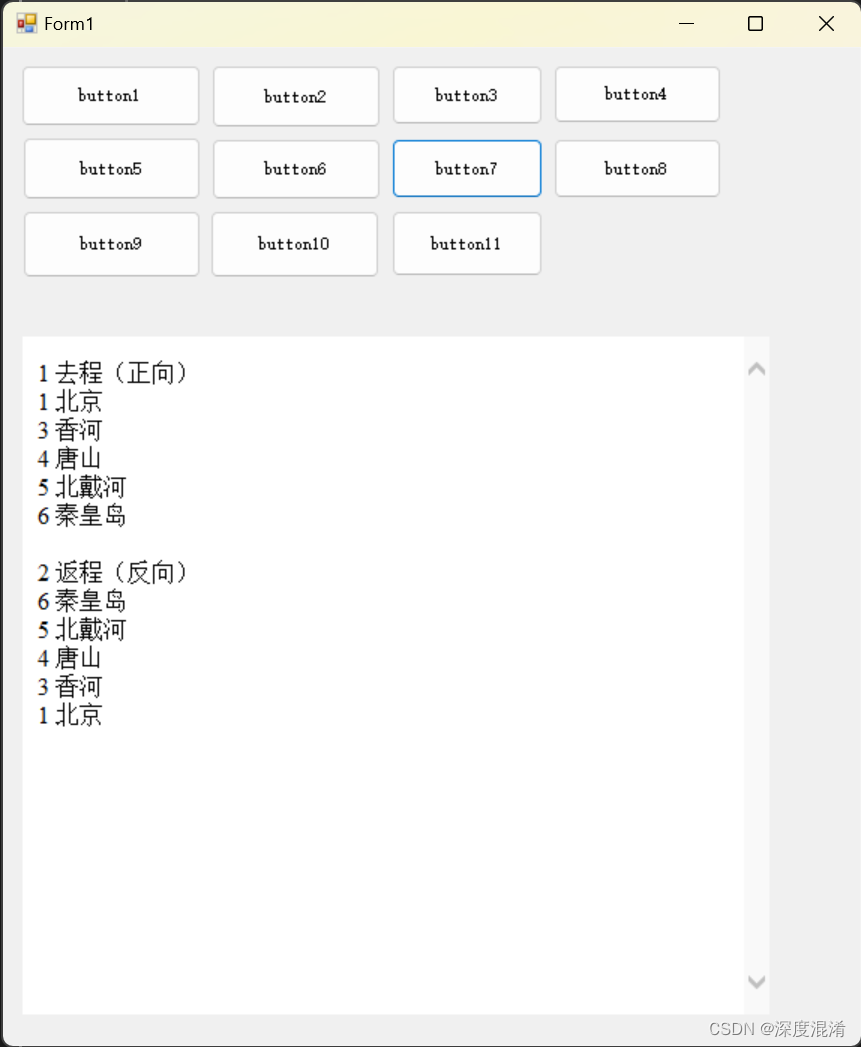
C#,《小白学程序》第七课:列表(List)应用之一“编制高铁车次信息表”
1 文本格式 /// <summary> /// 车站信息类 class /// </summary> public class Station { /// <summary> /// 编号 /// </summary> public int Id { get; set; } 0; /// <summary> /// 车站名 /// </summary>…...

周报/月报 Prompt
前言 用 AI 写好一份周报或月报。 文章目录 前言一、目的二、Prompt 设计原则三、模板 一、目的 简单的日程,扩写成一篇高质量的周报; 二、Prompt 设计原则 角色 目标 背景 要求 三、模板 内容生成模板 你是我的周报助手,根据我的工作…...

c++ 学习 之 构造函数的分类和调用类型 深入学习
正文 构造函数是在C中用于创建和初始化对象的特殊函数。构造函数可以根据不同的特性和参数进行分类,以下是一些常见的构造函数分类和详细讲解它们的调用方式: 默认构造函数: 默认构造函数是一个特殊的构造函数,它没有参数&#x…...

Royal TSX 6 Mac多协议远程软件
Royal TSX是一款功能强大的远程桌面管理软件,适用于Mac操作系统。它允许用户通过一个集成的界面来管理和访问多个远程计算机和服务器。 Royal TSX支持多种远程协议,包括RDP、VNC、SSH、Telnet和FTP等,可以方便地连接到Windows、Linux、Mac和其…...

远程管理通道安全SSH协议主机验证过程
可以使用SSH协议进行远程管理通道安全保护,其中涉及的主要安全功能包括主机验证、数据加密性和数据完整性保护。 这里要注意的是【主机验证】和【身份验证】的区别,主机验证是客户端确认所访问的服务端是目标访问对象,比如从从客户端A(192.16…...

.NET 操作 TDengine .NET ORM
TDengine 是国内比较流的时序库之一,支持群集并且免费,在.NET中资料比较少,这篇文章主要介绍SqlSugar ORM来操作TDengine 优点: 1、SqlSugar支持ADO.NET操作来实现TDengine,并且支持了常用的时间函数、支持联表、分…...
——视图(View))
SQL Server对象类型(3)——视图(View)
1. 视图概念 与Oracle中的视图类似,SQL Server中的视图也是一种虚的、通过一个查询定义的逻辑对象,主要用于集中、简化、定制用户需求,控住其底层表安全,以及应用系统提供向后兼容等方面。 --注: 1)上述内容中的“虚的”,表示视图本身并不实际包含和存储数据,SQL Ser…...
【LeetCode】剑指 Offer <二刷>(1)
目录 前言: 题目:剑指 Offer 03. 数组中重复的数字 - 力扣(LeetCode) 题目的接口: 解题思路: 代码: 过啦!!! 写在最后: 前言: …...

MySQL事物和存储引擎
事务 一、MySQL事务的概念 事务是一种机制、一个操作序列,包含了一组数据库操作命令,并且把所有的命令作为一个整体一起向系统提交或撤销操作请求,即这一组数据库命令要么都执行,要么都不执行。 事务是一个不可分割的工作逻辑单…...

代码随想录算法训练营Day51 | 309. 最佳买卖股票时机含冷冻期 | 714. 买卖股票的最佳时机含手续费 | 股票总结
文章目录 309. 最佳买卖股票时机含冷冻期标准 dp机智的分析解法 714. 买卖股票的最佳时机含手续费贪心算法 股票总结 309. 最佳买卖股票时机含冷冻期 题目链接 | 解题思路 标准 dp 本题多了冷却期的条件,将原本的两个状态变得更复杂了。变化在于,如果…...
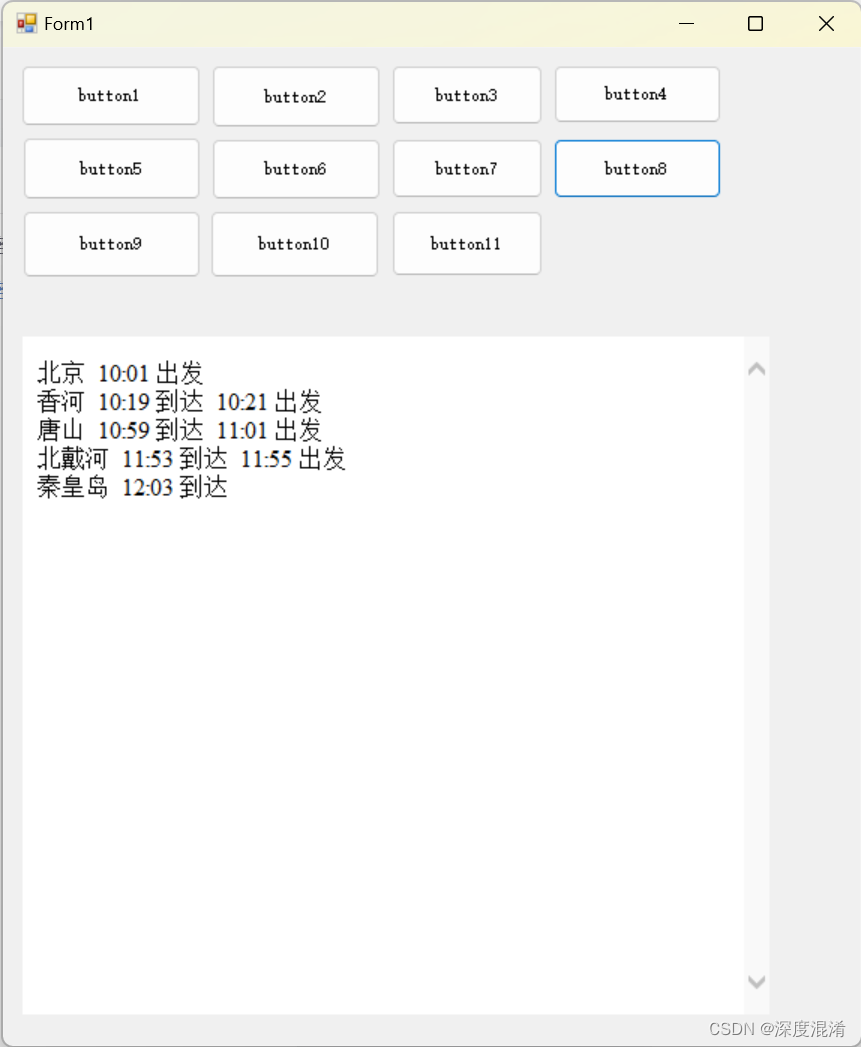
C#,《小白学程序》第八课:列表(List)应用之二“编制高铁列车时刻表”
1 文本格式 /// <summary> /// 车站信息类 class /// </summary> public class Station { /// <summary> /// 编号 /// </summary> public int Id { get; set; } 0; /// <summary> /// 车站名 /// </summary&g…...
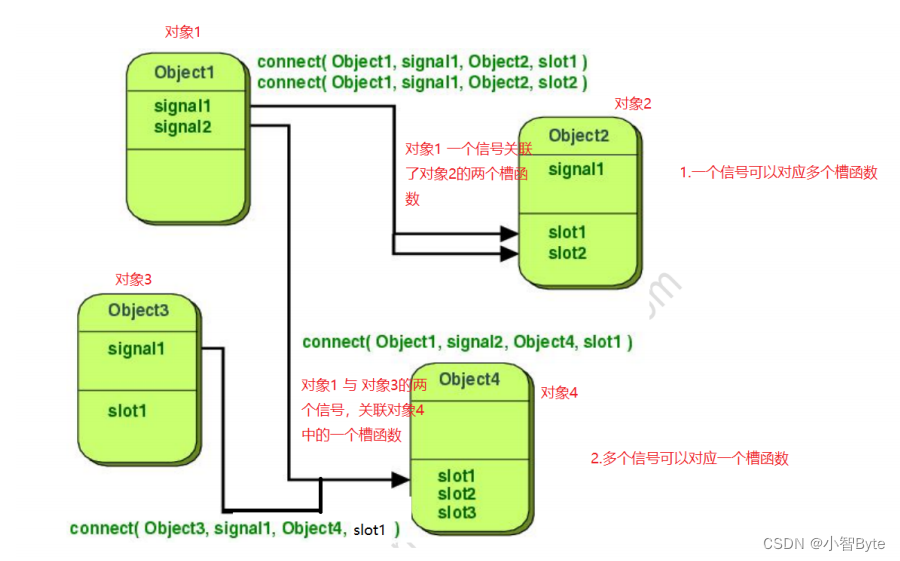
2、QT的信号与槽
一、什么是信号与槽 一个对象发送一个信号出去,另外一个对象接收到该信号后,会触发相应的槽函数 二、信号与槽的语法 connect(信号的发送者,SIGNAL(信号名称),信号的接收者,SLOT(槽函数)); 1、写法: QT 4 的写法 connect(sende…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...
