c语言每日一练(13)
前言:
每日一练系列,每一期都包含5道选择题,2道编程题,博主会尽可能详细地进行讲解,令初学者也能听的清晰。每日一练系列会持续更新,上学期间将看学业情况更新。
五道选择题:
1、程序运行的结果为()
#include<stdio.h>
int main()
{
int x=1.9;
x++;
printf("%d",x);
}A、1 B、2 C、2.9 D、3
解析:简单题,考察的是你对于整型变量的理解整型变量如果初始值被赋予小数,那么在vs编译器上就会直接将小数部分给舍去,也就是说,代码1中给x赋予1.9,实际上只是给x赋予1,接着走到x++,使x=2,所以最后打印出来的结果就是2,选B
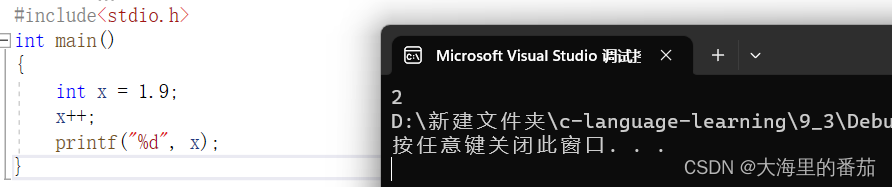

2、设有整型变量a,b,c,它们的初值是1,运行表达式++a| |++b&&++c后,a,b,c的值分别是 ()
A、2,1,1 B、2,2,2 C、2,2,1 D、2,1,2
解析:易错题,考察||(或)运算和&&(且)运算的运用,||运算只要一边为真即为真,所以当我们判定完一边为真的时候另一边就不用再判定,计算机会直接跳过。&&运算,两边都为真才为真,只要有一边为假就为假,所以一旦发现一边为假则不再判定另一边。
跟据规则走,首先遇到的是++a,先++后使用,a=2,2为真,是||运算,所以后面的部分不进行,连带着&&也没有进行,所以最后a=2,b=1,c=1,选A
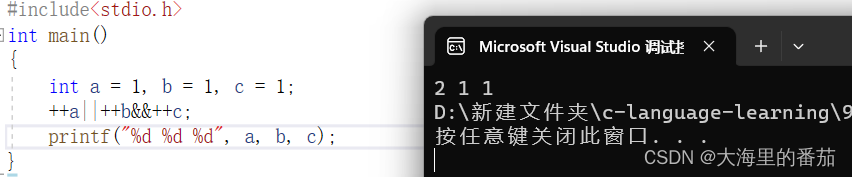
3、以下程序运行的结果为()
#include<stdio.h>
int main()
{int x = 5;int i = 0, j = 0, k = 0;x = (i = 4, j = 16, k = 32);printf("%d %d %d %d", x,i,j,k);
}A、5,4,16,32 B、5,0,0,0 C、32,4,16,32 D、32,0,0,0
解析:考察你对于逗号表达式的理解,逗号表达式从左往右进行,整个表达式的结果为最后一个表达式。
从左往右走,首先给i赋值为4,接着给j赋值为16,最后来到最后一个表达式,k=32,而根据逗号表达式的运行可知整个表达式的结果也是k=32,所以最后是x=k=32,同时对x和k赋值,所以x和k最后均为32,综上所述,i=4,j=16,x=k=32,所以最后打印出来的结果为32,4,16,32选C
 4、有如下程序,程序运行后的输出结果是()
4、有如下程序,程序运行后的输出结果是()
#include <stdio.h>
int main()
{
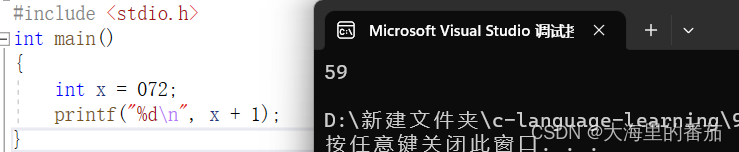
int x = 072;
printf("%d\n", x+1);
}A、72 B、73 C、115 D、59
解析:基础题,考察你对细节的掌控,八进制数的前缀为0,十六进制的前缀为0x,十进制数没有前缀。所以该程序赋值给x的值是一个八进制的72,转换为十进制就是2*1+7*8=58,最后打印出x+1即59,故选D
5、若想定义 int 型变量 a,b,c,d 并都赋值为 1,以下写法中错误的
是
A、int a=b=c=d=1;
B、int a=1, b=1, c=1, d=1;
C、int a,b,c,d; a=b=c=d=1;
D、int a,b,c,d=1; a=b=c=d;
解析:一个一个走,先看A选项,A选项的操作并没有定义b,c,d这三个整型变量,故A错误,B选项挨个定义,没有问题,B正确。C选项全部定义完了再赋值,C正确,D选项,先定义a,b,c,d四个变量的同时给d赋值为1,最后令a=b=c=d,令a,b,c与d相等,所以最后,a,b,c,d均为1,D正确,综上所述,选A
编程题1:
剑指 Offer 10- I. 斐波那契数列 - 力扣(LeetCode)
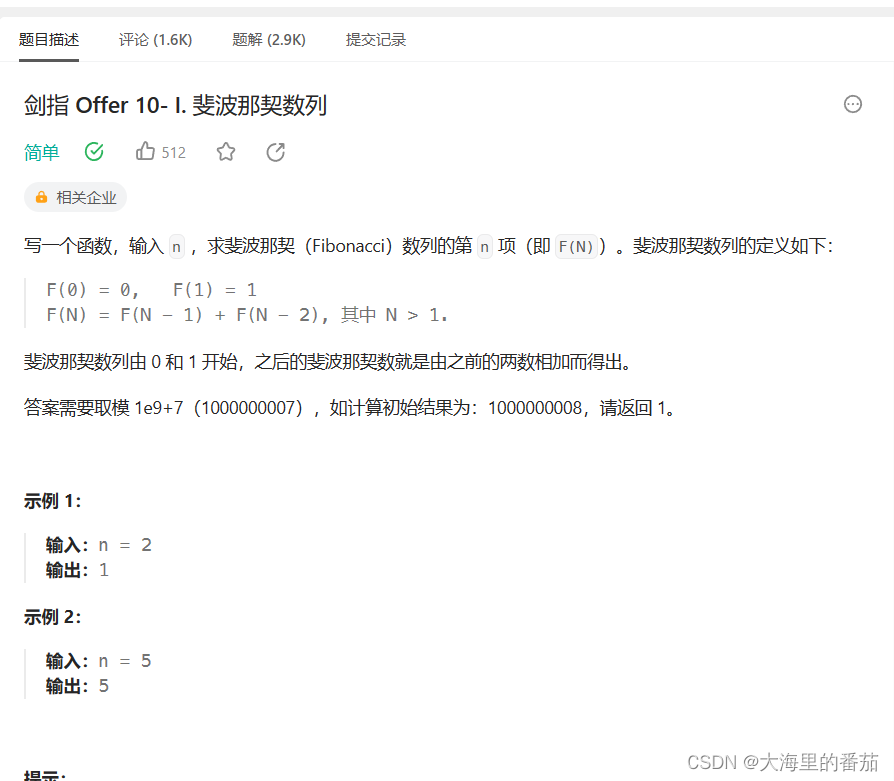
提示:记得取模,一开始博主也没有取模,想半天,哈哈

int fib(int n) {if (n == 0){return 0;}if (n <= 2){return 1;}//以上特殊情况单独处理下int f1 = 1; int f2 = 1; int f3 = 0; int i = 0;for (i = 3; i <= n; i++)//我们一开始计算的就是第三个斐波那契数,所以令i=3{f3 = (f1 + f2) % 1000000007;//先储存下一个斐波那契数f1 = f2;f2 = f3;//进行数据更新}return f3;//返回目标
}编程题2:
134. 加油站 - 力扣(LeetCode)

提示:此题较难,建议学习贪心算法之后再过来进行,这里博主并没有使用贪心算法,使用最朴实无华的方法通过的,目的是让大家能够感受一下代码的严谨。拷贝博主的代码有时也是通不过的,因为博主没有使用技巧答题,当你网络不好时可能会因为超出时间限制而失败,多试几次就可以。
int canCompleteCircuit(int* gas, int gasSize, int* cost, int costSize) {int oil = 0;int i = 0;if(gasSize==1)//只有一个单独处理{if(gas[0]>=cost[0])return 0;}for (i = 0; i < gasSize; i++){int tmp = i;//不要在函数内对循环变量操作,因此使用tmp来间接操作int flag = 1;//判定是否可以行进的变量oil = gas[tmp];if (oil > cost[tmp]){oil -= cost[tmp];for (++tmp; tmp < gasSize; tmp++){oil += gas[tmp];oil -= cost[tmp];if (oil < 0){flag = 0;break;}}if (flag == 0){continue;}for (tmp = 0; tmp < gasSize; tmp++){oil += gas[tmp];oil -= cost[tmp];if (tmp == i){break;}if (oil < 0){flag = 0;break;}}if (flag == 1){return tmp;}else{continue;}}else{continue;}}return -1;
}好了,今天的练习到这里就结束了,感谢各位友友的来访,祝各位友友前程似锦O(∩_∩)O
相关文章:

c语言每日一练(13)
前言:每日一练系列,每一期都包含5道选择题,2道编程题,博主会尽可能详细地进行讲解,令初学者也能听的清晰。每日一练系列会持续更新,上学期间将看学业情况更新。 五道选择题: 1、程序运行的结果…...
(2D转换transform 位移 旋转 缩放))
H5 + C3基础(六)(2D转换transform 位移 旋转 缩放)
2D转换transform & 2D转换transform平移利用平移百分比优化盒子水平垂直居中 旋转指定2d变换的中心点 transform-origin 缩放2d转换简写 2D转换transform 所谓2D转换,就是在二维坐标系内进行各种操作,包括平移,转动,缩放等等…...
2023最新 Electron.js 桌面应用开发教程(基础篇)更新中
Electron是什么? Electron是一个使用 JavaScript、HTML 和 CSS 构建桌面应用程序的框架。 嵌入 Chromium 和 Node.js 到 二进制的 Electron 允许您保持一个 JavaScript 代码代码库并创建 在Windows上运行的跨平台应用 macOS和Linux Electron Fiddle 运行实例 Ele…...

【ES】笔记-Set集合实践
JS <script>let arr[1,2,3,4,5,4,3,2,1];//1.数组去重let result0[...new Set(arr)];console.log(数组去重${result0});//2.交集let arr2[4,5,6,5,6];let result[...new Set(arr)].filter(item>{let s2new Set(arr2);//4 5 6if(s2.has(item)){return true;}else{retur…...
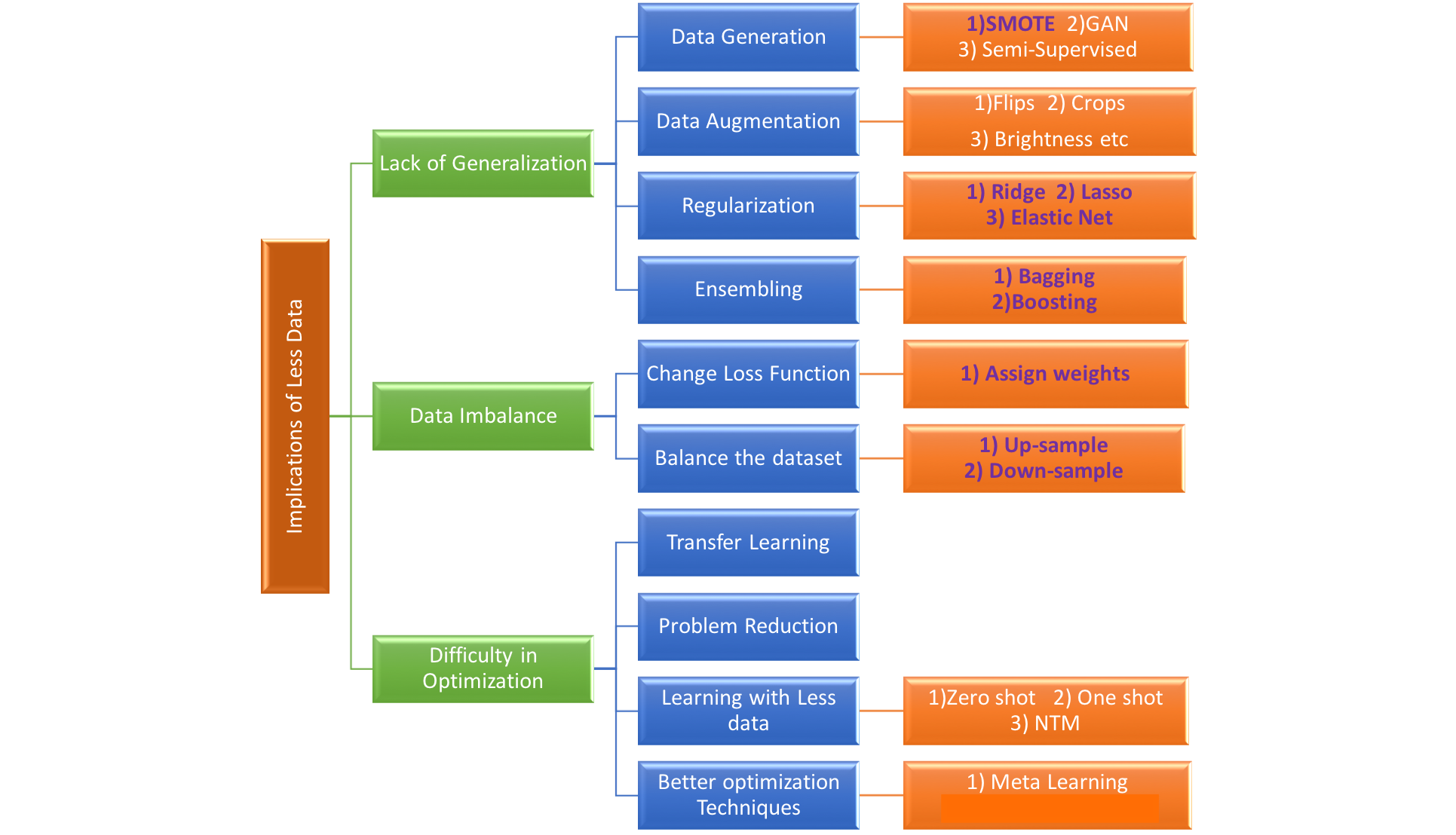
缺陷或负样本难以收集怎么办?使用生成式模型自动生成训练样本,image-to-image Stable diffusion
文章大纲 样本稀疏与对应的解决方案如何解决工业缺陷检测小样本问题参考1:AIDG(Artificial Intelligent Defect Generator)参考2:灵感来源 : Image-to-Image Diffusion Models参考文献与学习路径参考博文数据集算法缺陷检测库hugging face样本稀疏与对应的解决方案 1.数据层面…...
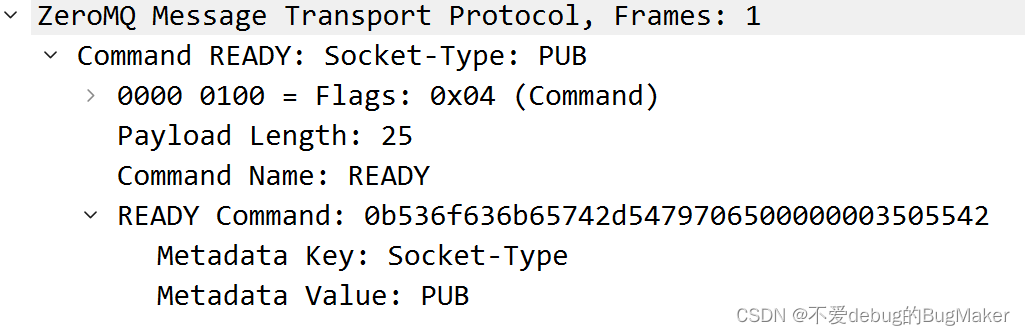
ZMTP协议
ZoreMQ Transport Protocol是一个传输层协议,用于ZMQ的连接的信息交互,本文档描述的是3.0协议,主要分析基于NULL Security Mechanism 协议语法 ZMTP由三部分组成,分别是 greeting、handshake、traffic 部分描述构成greeting描述…...

ubuntu18安装中文环境
1. 安装中文语言包 首先,我们需要安装中文语言包。打开终端,输入以下命令: sudo apt-get install language-pack-zh-hans 这个命令会下载并安装中文语言包。安装完成后,我们需要重新启动系统(reboot)。 2. 安装中文输入法 安…...
怎么提取视频中的音乐保存到本地?其实方法很简单
当你想要使用视频中的音乐时,你可以考虑将它从视频中提取出来。这可以用于制作音频样本集,制作铃声或其他音频素材,或者向其他人展示视频的音乐部分而无需显示视频本身。如果你是一位音乐制作人员,你可能会需要一些特定类型的音效…...
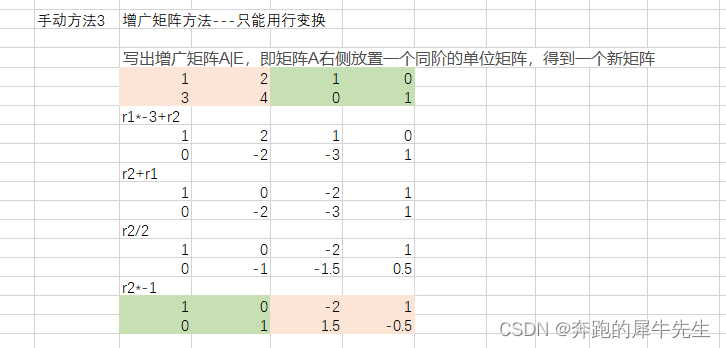
线性代数的学习和整理18:矩阵的秩的各种定理, 秩和维度(未完成)
目录 1 矩阵的秩 矩阵的秩 2 求秩的方法 矩阵的维度秩 矩阵的维度 向量的模,矩阵的模-没有把,难道是面积? 矩阵的平直概念 5 矩阵的初等变换(矩阵等价概念的引出) 1 为什么要引入矩阵的“秩” 这个概念&#x…...
)
UVa11374 Airport Express(Dijkstra)
题意 给出经济路线以及商业路线,在给出起始点s,终止点e,在只能使用其中一个商业路线 的情况下输出最短路径 思路 如果选择商业路线为从u到v,则需要从s->u,u->v,v->e点的路径最短。使用Dijkstra计算出从s点…...

hadoop的hdfs中避免因节点掉线产生网络风暴
hadoop的hdfs中避免因节点掉线产生网络风暴 控制节点掉线RPC风暴的参数 三个参数都是hdfs-site.xml中参数,具体可以参考apache hadoop官网,其实块的复制速度有两个方面决定,一是namenode分发任务的速度,二则是datanode之间进行复…...

2023年高教社杯 国赛数学建模思路 - 案例:最短时间生产计划安排
文章目录 0 赛题思路1 模型描述2 实例2.1 问题描述2.2 数学模型2.2.1 模型流程2.2.2 符号约定2.2.3 求解模型 2.3 相关代码2.4 模型求解结果 建模资料 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 最短时…...
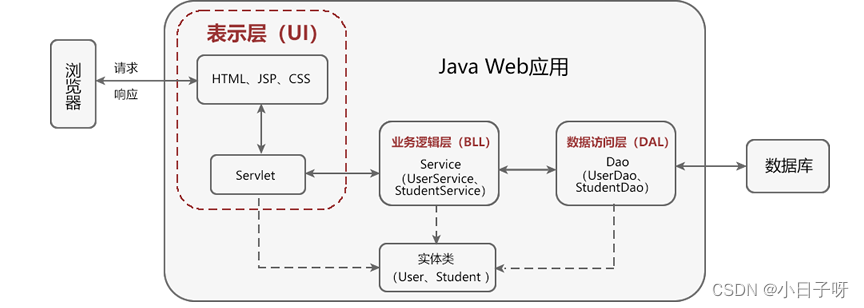
Spring MVC介绍
MVC模式是什么 MVC 模式,全称为 Model-View-Controller(模型-视图-控制器)模式,它是一种软件架构模式,其目标是将软件的用户界面(即前台页面)和业务逻辑分离,使代码具有更高的可扩展…...
5年测试在职经验之谈:2年功能测试、3年自动化测试,从入门到不可自拔...
毕业3年了,学的是环境工程专业,毕业后零基础转行做软件测试。 已近从事测试行业8年了,自己也从事过2年的手工测试,从事期间越来越觉得如果一直在手工测试的道路上前进,并不会有很大的发展,所以通过自己的努…...

【Python数据分析】数据分析之numpy基础
实验环境:建立在Python3的基础之上 numpy提供了一种数据类型,提供了数据分析的运算基础,安装方式 pip install numpy导入numpy到python项目 import numpy as np本文以案例的方式展示numpy的基本语法,没有介绍语法的细枝末节&am…...

Swift 如何从图片数据(Data)检测原图片类型?
功能需求 如果我们之前把图片对应的数据(Data)保持在内存或数据库中,那么怎么从 Data 对象检测出原来图片的类型呢? 如上图所示:我们将 11 张不同类型的图片转换为 Data 数据,然后从 Data 对象正确检测出了原图片类型。 目前,我们的代码可以检测出 jpeg(jpg), tiff,…...

【ES6】 JavaScript 中的Object.assign
Object.assign() 是 JavaScript 中的一个方法,它用于复制源对象的所有可枚举属性到目标对象。该方法会返回目标对象。 这是其基本用法: let target Object.assign({}, source);在这个例子中,source 对象的所有可枚举属性都被复制到了 targ…...

Redis缓存和持久化
目录 Redis缓存 什么是缓存 缓存更新策略编辑 业务场景 缓存穿透 常见的解决方案 缓存雪崩 解决方案 缓存击穿 解决方案 Redis持久化 RDB持久化 执行时机 RDB方式bgsave的基本流程 AOF持久化 RDB和AOF的对比编辑 Redis主从 数据同步原理 总结 Redis缓存 …...
:多通道分离与合并)
OpenCV(六):多通道分离与合并
目录 1.多通道分离split() 2.多通道合并merge() 3.Android JNI demo 1.多通道分离split() void cv::split ( InputArray m, OutputArrayOfArrays mv ) m:待分离的多通道图像。 mv:分离后的单通道图像,为向量vector形式。 2.多通道合并merge…...

Sql单行数据查询为多行
数据量小可以,数据量大时间太久 select distinct regexp_substr("fixed_option", [^,],1,level) c1 from "MATERIAL"."BasicInfo_Dishes_Summary" A where "fixed_option" is not NULL AND "dish_name"地三鲜…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
