【Atcoder】 [ARC144D] AND OR Equation
题目链接
Atcoder方向
Luogu方向
题目解法
考虑满足条件 2 2 2 的形式为 a n = p 0 + ∑ i ∈ n p i a_n=p_0+\sum\limits_{i\in n}p_i an=p0+i∈n∑pi
这是一步很巧妙的转化,神奇地利用了 & \& & 和 ∣ | ∣ 的性质,把求 a a a 的方案数转化为求 p p p 的方案数
考虑如何满足条件 1 1 1,令 p i < 0 p_i<0 pi<0 的和为 X X X, p i > 0 p_i>0 pi>0 的和为 Y Y Y,那么 min { a i } = X + p 0 , max { a i } = Y + p 0 \min\{a_i\}=X+p_0,\;\max\{a_i\}=Y+p_0 min{ai}=X+p0,max{ai}=Y+p0
所以可以得出 − X ≤ p 0 ≤ k − Y -X\le p_0\le k-Y −X≤p0≤k−Y,所以合法的 p 0 p_0 p0 取值有 k − ( Y − X ) + 1 k-(Y-X)+1 k−(Y−X)+1 种
考虑 Y − X = ∑ ∣ a i ∣ Y-X=\sum |a_i| Y−X=∑∣ai∣,所以 k − ( Y − X ) − 1 = k + 1 − ∑ ∣ p i ∣ k-(Y-X)-1=k+1-\sum{|p_i|} k−(Y−X)−1=k+1−∑∣pi∣
考虑枚举 p p p 中非 0 0 0 的个数,正负性有 2 i 2^i 2i 种, s s s 表示绝对值之和,然后就是 s s s 个球分给 i i i 个盒子,每个盒子不为空,且要分完的方案数(经典问题),最后再乘上 p 0 p_0 p0 的取值方案数
所以 A n s = ∑ i = 0 n ( n i ) 2 i ∑ s = i k + 1 ( s − 1 i − 1 ) ( k + 1 − s ) Ans=\sum\limits_{i=0}^{n}\binom{n}{i}2^i\sum\limits_{s=i}^{k+1}\binom{s-1}{i-1}(k+1-s) Ans=i=0∑n(in)2is=i∑k+1(i−1s−1)(k+1−s)
只考虑 ∑ s = i k + 1 ( s − 1 i − 1 ) ( k + 1 − s ) = ∑ s = i k + 1 ( k + 1 ) ( s − 1 i − 1 ) − s ( s − 1 i − 1 ) = ( k + 1 ) ( k + 1 i ) − ∑ s = i k + 1 i ( s i ) = ( k + 1 ) ( k + 1 i ) − i ( k + 2 i + 1 ) \sum\limits_{s=i}^{k+1}\binom{s-1}{i-1}(k+1-s)\\=\sum\limits_{s=i}^{k+1}(k+1)\binom{s-1}{i-1}-s\binom{s-1}{i-1} \\=(k+1)\binom{k+1}{i}-\sum\limits_{s=i}^{k+1}i\binom{s}{i} \\=(k+1)\binom{k+1}{i}-i\binom{k+2}{i+1} s=i∑k+1(i−1s−1)(k+1−s)=s=i∑k+1(k+1)(i−1s−1)−s(i−1s−1)=(k+1)(ik+1)−s=i∑k+1i(is)=(k+1)(ik+1)−i(i+1k+2)
展开,然后化简,这里就不细写了
最后化简出来是 A n s = ∑ i = 0 n ( n i ) 2 i ( k + 1 i + 1 ) Ans=\sum\limits_{i=0}^{n}\binom{n}{i}2^i\binom{k+1}{i+1} Ans=i=0∑n(in)2i(i+1k+1)
直接求解即可,时间复杂度 O ( n ) O(n) O(n)
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N=300100,P=998244353;
int n,k,fac[N],inv[N];
inline int read(){int FF=0,RR=1;char ch=getchar();for(;!isdigit(ch);ch=getchar()) if(ch=='-') RR=-1;for(;isdigit(ch);ch=getchar()) FF=(FF<<1)+(FF<<3)+ch-48;return FF*RR;
}
int qmi(int a,int b){int res=1;for(;b;b>>=1){if(b&1) res=res*a%P;a=a*a%P;}return res;
}
int C(int a,int b){ return fac[a]*inv[b]%P*inv[a-b]%P;}
signed main(){n=read(),k=read();fac[0]=1;for(int i=1;i<=n+1;i++) fac[i]=fac[i-1]*i%P;inv[n+1]=qmi(fac[n+1],P-2);for(int i=n;i>=0;i--) inv[i]=inv[i+1]*(i+1)%P;int ans=0,res=(k+1)%P;for(int i=0,pw=1;i<=n;i++,pw=pw*2%P){ans=(ans+C(n,i)*pw%P*res%P*inv[i+1])%P;res=res*((k+1-i-1)%P)%P;}printf("%lld",ans);return 0;
}相关文章:

【Atcoder】 [ARC144D] AND OR Equation
题目链接 Atcoder方向 Luogu方向 题目解法 考虑满足条件 2 2 2 的形式为 a n p 0 ∑ i ∈ n p i a_np_0\sum\limits_{i\in n}p_i anp0i∈n∑pi 这是一步很巧妙的转化,神奇地利用了 & \& & 和 ∣ | ∣ 的性质,把求 a a a 的…...

python使用字典暴力解析wifi密码
前言 最近无wifi可用,搜到了很多高质量但是没有密码的WiFi,我在想应该可以用python调用常见的wifi字典包来暴力破解一下这些WiFi,也许可以成功 原理 使用pip install pywifi命令安装pywifi 使用它调用本机网卡,设置wifi加密方式,对字典包扫描密码逐个尝试 扫描失败的密码会被…...

java八股文面试[多线程]——synchronized锁升级详细流程
偏向锁 偏向锁是JDK6中的重要引进,因为HotSpot作者经过研究实践发现,在大多数情况下,锁不仅不存在多线程竞争,而且总是由同一线程多次获得,为了让线程获得锁的代价更低,引进了偏向锁。 偏向锁是在单线程执…...

ui网页设计实训心得
ui网页设计实训心得篇一 通过这次实训对这门课程的学习,做好网页,并不是一件容易的事,它包括网页的选题、 内容采集整理、 图片的处理、 页面的排版设置、 背景及其整套网页的色调等很多东西。 所以我得出一下总结: 一、 准备资…...

论文阅读_扩散模型_DDPM
英文名称: Denoising Diffusion Probabilistic Models 中文名称: 去噪扩散概率模型 论文地址: http://arxiv.org/abs/2006.11239 代码地址1: https://github.com/hojonathanho/diffusion (论文对应代码 tensorflow) 代码地址2: https://github.com/AUTOM…...
:数据结构)
菜鸟教程《Python 3 教程》笔记(15):数据结构
菜鸟教程《Python 3 教程》笔记(15) 15 数据结构15.1 将列表当作队列使用15.2 遍历技巧 笔记带有个人侧重点,不追求面面俱到。 15 数据结构 出处: 菜鸟教程 - Python3 数据结构 15.1 将列表当作队列使用 在列表的最后添加或者弹…...

CH05_介绍重构名录
重构的记录格式 每个重构手法都有5个部分。 名称(name) 要建造一个重构词汇表,名称是很重要的。 速写(sketch) 名称之后是一个简单的速写(sketch);这部分可以帮助你更快找到你所…...
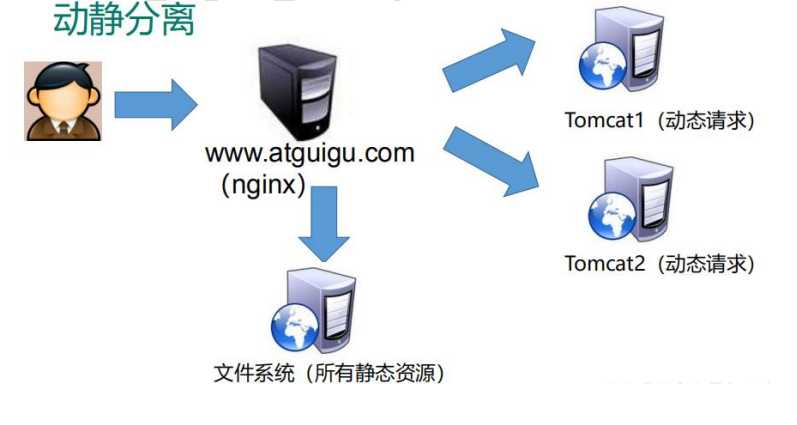
1、Nginx 简介
文章目录 1、Nginx 简介1.1 Nginx 概述1.2 Nginx 作为 web 服务器1.3 正向代理1.4 反向代理1.5 负载均衡1.6 动静分离 【尚硅谷】尚硅谷Nginx教程由浅入深 志不强者智不达;言不信者行不果。 1、Nginx 简介 1.1 Nginx 概述 Nginx (“engine x”) 是一个高性能的 HT…...

C++之——宏
宏(Macro)是一种在编程语言中使用的符号,通常用于将一段代码片段替换为另一段代码。宏在代码中起到了预处理的作用,它们在编译代码之前被处理和展开。宏通常用于简化代码、提高代码的可读性、实现代码重用以及引入编译时常量。 在…...

代码随想录打卡—day56—【编辑距离】— 9.2 编辑距离系列
1 583. 两个字符串的删除操作 583. 两个字符串的删除操作 【注意点1】感觉和下面这题很像。就是一模一样,return变一下就是。 1143. 最长公共子序列 【注意点2】注意这题和day55的最后一题的区别,本题求的是最大长度,那题求的是组合方式。…...

uni-app app端.m3u8类型流的播放
1.开发环境:HBuilderX3.8.7、uni-app、vue2.0、view2.0、uni-ui 2.实现通过web-view 嵌入H5页面,进行视频流自动播放。 注意事项: 如果只是在android端可以直接使用.flv格式的视频流; 如果App需要支持ios就可以考虑一下播放.m3u8格…...

使用proxy_pool来为爬虫程序自动更换代理IP | 开源IP代理
1. 前言 之前做爬虫的时候,经常会遇到对于一个网页,使用同一个IP多次会被禁掉IP的问题,我们可以自己手动更换代理IP再继续这个问题但多少会有点麻烦,我对于一个懒人来说,手动更换IP太麻烦,而且也不符合程序员懒惰的美德,于是便有了下面的故事。proxy_pool 是一个开源的代…...

【易售小程序项目】修改“我的”界面前端实现;查看、重新编辑、下架自己发布的商品【后端基于若依管理系统开发】
文章目录 “我的”界面修改效果界面实现界面整体代码 查看已发布商品界面效果商品数据表后端上架、下架商品ControllerMapper 界面整体代码back方法 编辑商品、商品发布、保存草稿后端商品校验方法Controller 页面整体代码 “我的”界面修改 效果 界面实现 界面的实现使用了一…...

Centos7 + Apache Ranger 2.4.0 部署
一、Ranger简介 Apache Ranger提供一个集中式安全管理框架, 并解决授权和审计。它可以对Hadoop生态的组件如HDFS、Yarn、Hive、Hbase等进行细粒度的数据访问控制。通过操作Ranger控制台,管理员可以轻松的通过配置策略来控制用户访问权限。 1、组件列表 # Service Name Liste…...
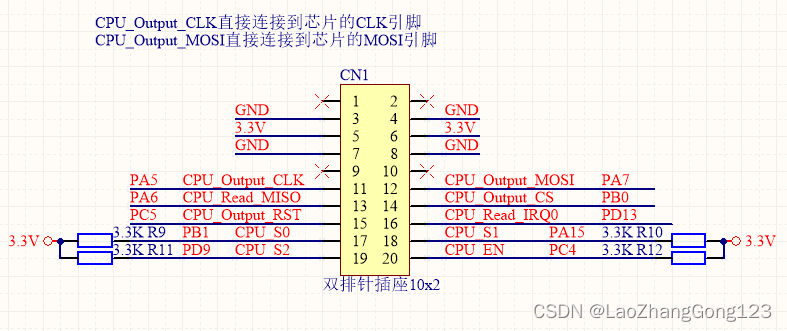
硬件SPI口扩展
在工控板设计中,经常会遇到扩展IO。具有相同的功能电路板接口相同,所以很容易采用排线方式连接到CPU主控板上,这种排线连接,我称之为总线。 现在的CPU引脚多,不扩展IO,使用模拟SPI,也可以实现&…...

【jsthree.js】全景vr看房进阶版
three小结: Scene场景 指包含了所有要渲染和呈现的三维对象、光源、相机以及其他相关元素的环境;场景可以被渲染引擎或图形库加载和处理,以生成最终的图像或动画 常见属性: scene.background new THREE.Color(0x000000); // …...

实战:基于卷积的MNIST手写体分类
前面实现了基于多层感知机的MNIST手写体识别,本章将实现以卷积神经网络完成的MNIST手写体识别。 1. 数据的准备 在本例中,依旧使用MNIST数据集,对这个数据集的数据和标签介绍,前面的章节已详细说明过了,相对于前面章…...

Ubuntu开启生成Core Dump的方法
C 文章目录 C1. 首先ulimit通过查看2. 执行下面的命令 Ubuntu下无法生成Core Dump解决方法 1. 首先ulimit通过查看 ulimit -a查看是core file size是否为0,若为0,通过以下方式设置size ulimit -c 1024或者 ulimit -c unlimited //size没有限制2. 执行…...
git视频教程Jenkins持续集成视频教程Git Gitlab Sonar教程
[TOC这里写自定义目录标题) https://edu.51cto.com/lesson/290903.html 欢迎使用Markdown编辑器 你好! 这是你第一次使用 Markdown编辑器 所展示的欢迎页。如果你想学习如何使用Markdown编辑器, 可以仔细阅读这篇文章,了解一下Markdown的基本语法知识。…...
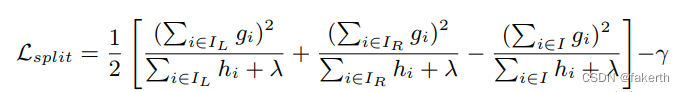
机器学习:Xgboost
Xgboost XGBoost(eXtreme Gradient Boosting)是一种机器学习算法,是梯度提升决策树(Gradient Boosting Decision Trees)的一种优化实现。它是由陈天奇在2014年开发并推出的。XGBoost是一种强大而高效的算法࿰…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...
