【洛谷】P3853 路标设置
原题链接:https://www.luogu.com.cn/problem/P3853
目录
1. 题目描述
2. 思路分析
3. 代码实现
1. 题目描述
2. 思路分析
整体思路:二分答案
由题意知,公路上相邻路标的最大距离定义为该公路的“空旷指数”。在公路上增设一些路标,使得公路的“空旷指数”最小。也就是满足最大值最小。我们就自然想到可以二分答案。
定义三个变量L,n,k分别表示公路的长度,原有路标的数量,以及最多可增设的路标数量。开一个数组a,数组的第i个元素a[i]表示原有路标与起点的距离。
我们这里又开了一个差值数组s,令s[i]=a[i]-a[i-1],这样就可以用数组s表示原有的两个相邻路标的距离。
令左边界l=0,右边界r=L。
套用二分模板,mid=(l+r)>>1。主要就是要写一个check()函数,设check()函数的形参为x,将mid传入x。我们定义一个cnt变量用于记录新增的路标数量,遍历s[i]数组,如果s[i]>x,我们就要新增一个路标(cnt++),同时我们判断剩余部分(s[i]-x)的长度和x的关系,如果剩余部分的长度比x大,我们就继续插路标(cnt++),直到num<=x。
for循环结束后,我们判断一下cnt(新增路标数量)和k(最多可增设的路标数量),如果cnt<=k,return true。否则return false。
3. 代码实现
#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N = 100010;
ll a[N], s[N], L, n, k, maxx;bool check(int x) {ll cnt = 0;for (int i = 1; i <= n; i++) {if (s[i] > x) {cnt++;int num = s[i] - x;while (num > x) {cnt++;num -= x;}}}if (cnt <= k) return true;else return false;
}int main() {cin >> L >> n >> k;for (int i = 1; i <= n; i++) {cin >> a[i];s[i] = a[i] - a[i - 1];}int l = 0, r = L;while (l + 1 < r) {int mid = (l + r) >> 1;if (check(mid)) r = mid;else l = mid;}cout << r << endl;return 0;
}
相关文章:

【洛谷】P3853 路标设置
原题链接:https://www.luogu.com.cn/problem/P3853 目录 1. 题目描述 2. 思路分析 3. 代码实现 1. 题目描述 2. 思路分析 整体思路:二分答案 由题意知,公路上相邻路标的最大距离定义为该公路的“空旷指数”。在公路上增设一些路标&…...

探索图像数据中的隐藏信息:语义实体识别和关系抽取的奇妙之旅
探索图像数据中的隐藏信息:语义实体识别和关系抽取的奇妙之旅 1. 简介 1.1 背景 关键信息抽取 (Key Information Extraction, KIE)指的是是从文本或者图像中,抽取出关键的信息。针对文档图像的关键信息抽取任务作为OCR的下游任务,存在非常…...

Gradle问题处理
目录 一、依赖搜索问题1.1 、Gradle不在本地 Maven 存储库中进行搜索一、依赖搜索问题 1.1 、Gradle不在本地 Maven 存储库中进行搜索 场景 build.gradle文件: buildscript {repositories {mavenLocal()google()mavenCentral()}dependencies...

架构:C4 Model
概念 C4说穿了就是几个要素:关系——带箭头的线、元素——方块和角色、关系描述——线上的文字、元素的描述——方块和角色里的文字、元素的标记——方块和角色的颜色、虚线框(在C4里面虚线框的表达力被极大的限制了,我觉得可以给虚线框更大…...

数据结构学习系列之顺序表的两种修改方式
方式1:根据顺序表中数据元素的位置进行修改,代码如下:示例代码: int modify_seq_list_1(list_t *seq_list,int pos, int data){if(NULL seq_list){printf("入参为NULL\n");return -1;}if( pos < 0 || pos > seq…...

React:props说明
props是只读对象(readonly) 根据单项数据流的要求,子组件只能读取props中的数据,不能进行修改props可以传递任意数据 数字、字符串、布尔值、数组、对象、函数、JSX import FileUpdate from ./FileUpdate; export default class …...
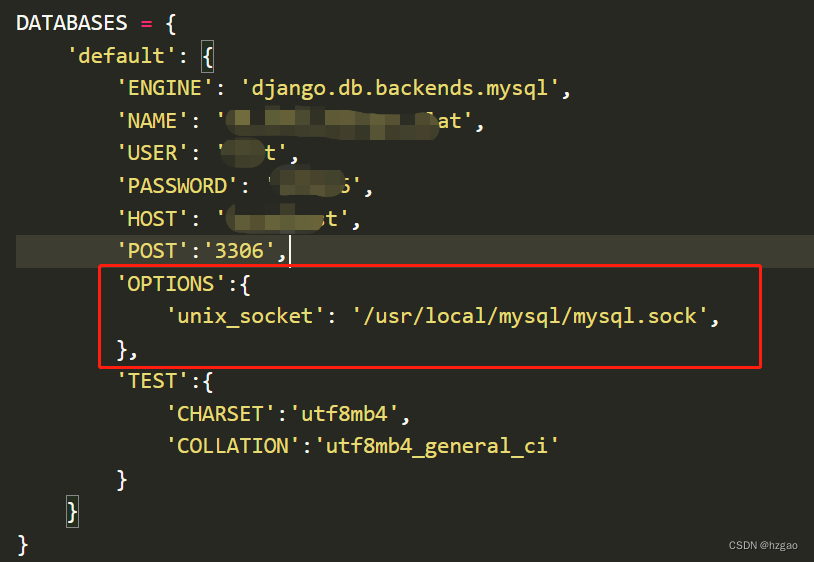
Can‘t connect to local MySQL server through socket ‘/tmp/mysql.sock‘
最近在用django框架开发后端时,在运行 $python manage.py makemigrations 命令时,报了以上错误,错误显示连接mysql数据库失败,查看了mysql数据库初始化配置文件my.cnf,我的mysql.sock文件存放路径配置在了/usr/local…...

C++的单例模式
忘记之前有没有写过单例模式了。 再记录一下: 我使用的代码: #ifndef SINGLETON_MACRO_HPP #define SINGLETON_MACRO_HPP#define SINGLETON_DECL(class_name) \ public: \static class_name& instance() { \static class_name s_instance; \return …...

Spring Boot 中 Nacos 配置中心使用实战
官方参考文档 https://nacos.io/zh-cn/docs/quick-start-spring-boot.html 本人实践 1、新建一个spring boot项目 我的spirngboot版本为2.5.6 2、添加一下依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-…...
学生管理系统VueAjax版本
学生管理系统VueAjax版本 使用Vue和Ajax对原有学生管理系统进行优化 1.准备工作 创建AjaxResult类,对Ajax回传的信息封装在对象中 package com.grg.Result;/*** Author Grg* Date 2023/8/30 8:51* PackageName:com.grg.Result* ClassName: AjaxResult* Descript…...

迭代器模式简介
概念: 迭代器模式是一种行为型设计模式,它提供了一种访问集合对象元素的方法,而无需暴露其内部表示。通过使用迭代器,可以按照特定顺序遍历集合中的元素。 特点: 将遍历和具体集合分离,使得能够独立地改…...

四方定理c++题解
题目描述 四方定理是数论中著名的一个定理,指任意一个自然数都可以拆成四个自然数的平方之和。例如: 251^22^22^24^2 对 25来说,还有其他方案: 250^20^23^24^2 以及 250^20^20^25^2 给定一个自然数 n ,请输出 n…...
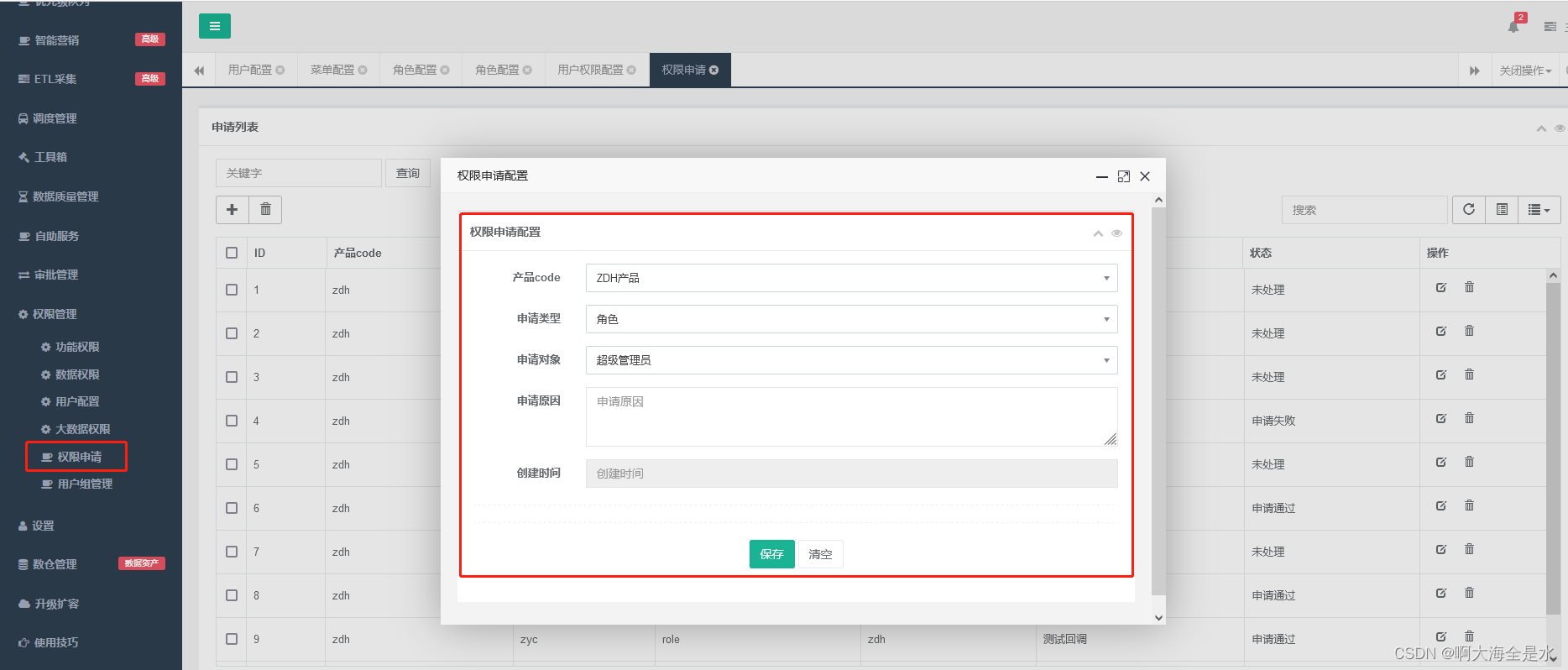
ZDH-权限模块
本次介绍基于ZDH v5.1.2版本 目录 项目源码 预览地址 安装包下载地址 ZDH权限模块 ZDH权限模块-重要名词划分 ZDH权限模块-菜单管理 ZDH权限模块-角色管理 ZDH权限模块-用户配置 ZDH权限模块-权限申请 项目源码 zdh_web: GitHub - zhaoyachao/zdh_web: 大数据采集,抽…...
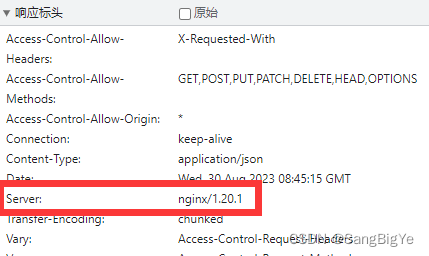
漏洞修复:在应用程序中发现不必要的 Http 响应头
描述 blablabla描述,一般是在返回的响应表头中出现了Server键值对,那我们要做的就是移除它,解决方案中提供了nginx的解决方案 解决方案 第一种解决方案 当前解决方案会隐藏nginx的版本号,但还是会返回nginx字样,如…...

什么是mkp勒索病毒,中了mkp勒索病毒怎么办?勒索病毒解密数据恢复
mkp勒索病毒是一种新兴的计算机木马病毒,它以加密文件的方式进行勒索,对用户的计算机安全造成了严重威胁。本文将介绍mkp勒索病毒的特征、影响以及应对措施,以便读者更好地了解和防范这种病毒。 一、mkp勒索病毒的特征 加密文件:…...

db2迁移至oracle
1.思路 (1)用java连接数据库(2)把DB2数据导出为通用的格式如csv,json等(3)导入其他数据库,比如oracle,mongodb。这个方法自由发挥的空间比较大。朋友说他会用springboot…...

webpack学习使用
...

按钮控件之2---QComboBox 复选按钮/复选框控件
1、常用函数: comboBox->addItem("cxq"); //添加下拉选项 combobox->clear(); //清空下拉项comboBox->setCurrentIndex(0);//设置当前的索引 int currentlndex(): //返回当前项的序号,第一个项的序号…...
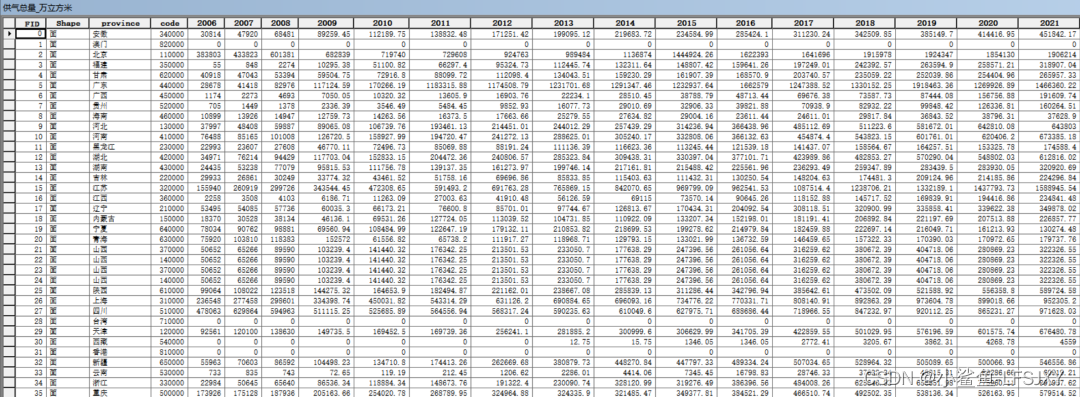
【数据分享】2006-2021年我国省份级别的燃气相关指标(免费获取\20多项指标)
《中国城市建设统计年鉴》中细致地统计了我国城市市政公用设施建设与发展情况,在之前的文章中,我们分享过基于2006-2021年《中国城市建设统计年鉴》整理的2006—2021年我国省份级别的市政设施水平相关指标、2006-2021年我国省份级别的各类建设用地面积数…...
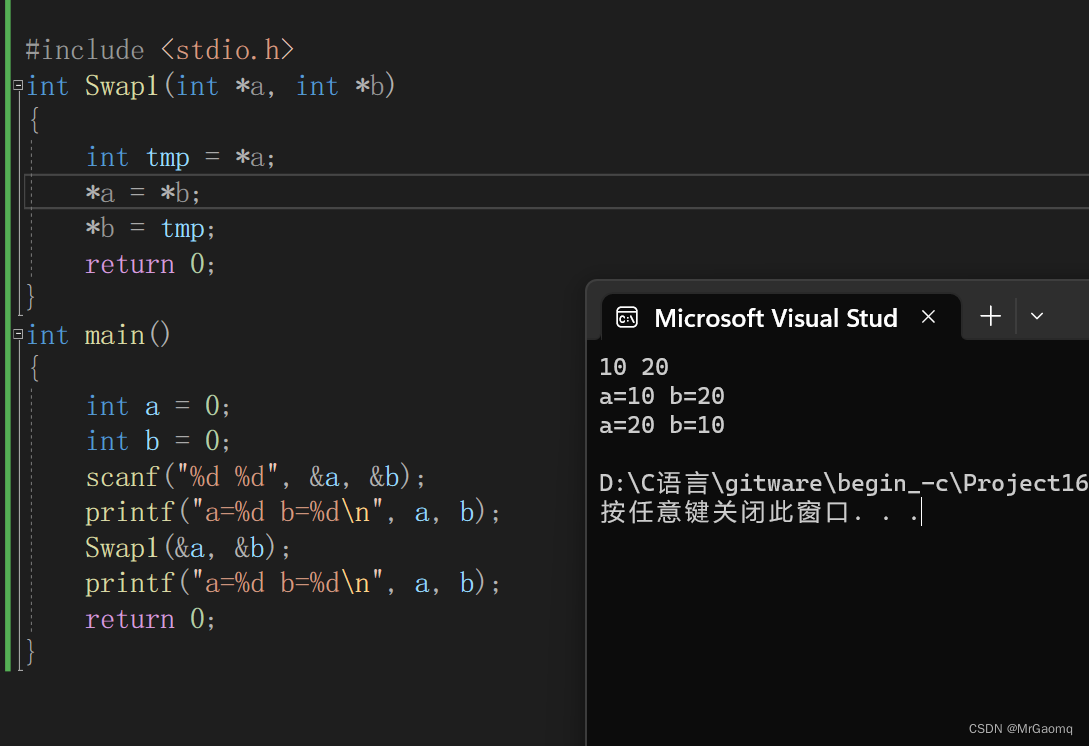
C语言深入理解指针(非常详细)(二)
目录 指针运算指针-整数指针-指针指针的关系运算 野指针野指针成因指针未初始化指针越界访问指针指向的空间释放 如何规避野指针指针初始化注意指针越界指针不使用时就用NULL避免返回局部变量的地址 assert断言指针的使用和传址调用传址调用例子(strlen函数的实现&a…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

