第六章,线性变换,1-线性变换、表示矩阵、线性算子
第六章,线性变换,1-线性变换、表示矩阵、线性算子
- 线性变换
- 表示矩阵
- 线性算子
- R 2 R^2 R2中特殊的线性变换
- 旋转变换算子
- 反射变换算子
- 投影变换算子
- 伸压变换算子
- 剪切变换算子
玩转线性代数(32)线性变换的相关概念的笔记,相关证明以及例子见原文
线性变换
一个将向量空间V映射到向量空间W的映射L,如果对所有的 v 1 , v 2 ∈ V v_1,v_2\in V v1,v2∈V及所有的标量 α \alpha α和 β \beta β,有 L ( α v 1 + β v 2 ) = α L ( v 1 ) + β L ( v 2 ) L(\alpha v_1+\beta v_2)=\alpha L(v_1)+\beta L(v_2) L(αv1+βv2)=αL(v1)+βL(v2)
则称L为V到W上的一个线性变换,记为 L : V → W L:V\rightarrow W L:V→W
判断方法:若L为V到W上的一个线性变换,等价于:
L ( v 1 + v 2 ) = L ( v 1 ) + L ( v 2 ) ; L ( λ v 1 ) = λ L ( v 1 ) L(v_1+v_2)=L(v_1)+L(v_2); L(\lambda v_1) = \lambda L(v_1) L(v1+v2)=L(v1)+L(v2);L(λv1)=λL(v1)
表示矩阵
对任一矩阵 A m ∗ n A_{m*n} Am∗n,可以定义一个由 R n R^n Rn到 R m R^m Rm的线性变换 L A L_A LA,称A为 L A L_A LA的表示矩阵。而每一线性变换均可由矩阵来定义,如果是 R n R^n Rn上的线性算子,则其对应矩阵为n阶方阵。
线性算子
如果V与W相同,称 L : V → V L:V\rightarrow V L:V→V为V上的一个线性算子,是一个向量空间到其自身的线性变换。
R 2 R^2 R2中特殊的线性变换
示意图见原文
旋转变换算子
A = ( cos θ − sin θ sin θ cos θ ) A=\begin{pmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{pmatrix} A=(cosθsinθ−sinθcosθ)
绕逆时针旋转 θ \theta θ角
反射变换算子
B 1 = ( 1 0 0 − 1 ) B_1=\begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} B1=(100−1)
x轴对称
B 2 = ( − 1 0 0 1 ) B_2=\begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix} B2=(−1001)
y轴对称
投影变换算子
C 1 = ( 1 0 0 0 ) C_1=\begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix} C1=(1000)
只取了x坐标,所以是投影到x轴
C 2 = ( 0 0 0 1 ) C_2=\begin{pmatrix} 0 & 0 \\ 0 & 1 \end{pmatrix} C2=(0001)
只取了y坐标,所以是投影到y轴
伸压变换算子
D 1 = ( t 0 0 1 ) D_1=\begin{pmatrix} t & 0 \\ 0 & 1 \end{pmatrix} D1=(t001)
x坐标缩放t倍,y不变
D 2 = ( 0 0 0 t ) D_2=\begin{pmatrix} 0 & 0 \\ 0 & t \end{pmatrix} D2=(000t)
x坐标不变,y缩放t倍
剪切变换算子
E 1 = ( 1 0 k 1 ) E_1=\begin{pmatrix} 1 & 0 \\ k & 1 \end{pmatrix} E1=(1k01)
x不变,将x坐标的k倍加到y上,离y轴越远(x绝对值越大)形变越大(垂直变换)
E 2 = ( 1 k 0 1 ) E_2=\begin{pmatrix} 1 & k \\ 0 & 1 \end{pmatrix} E2=(10k1)
y不变,将y坐标的k倍加到x上,离x轴越远(y绝对值越大)形变越大(水平变换)
相关文章:

第六章,线性变换,1-线性变换、表示矩阵、线性算子
第六章,线性变换,1-线性变换、表示矩阵、线性算子 线性变换表示矩阵 线性算子 R 2 R^2 R2中特殊的线性变换旋转变换算子反射变换算子投影变换算子伸压变换算子剪切变换算子 玩转线性代数(32)线性变换的相关概念的笔记,相关证明以及例子见原文…...

15个关于AI的Github库
这里是我们精选的创新项目列表(排名不分先后),这些项目正在机器学习和人工智能领域蓬勃发展 1:privateGPT 作者:imartinezGithub 星数:16.7K描述:利用LLM的力量,在没有互联网连接的情…...

在Jupyter 中 from XXX import * 报错
在Jupyter 中 导入模块会出现 from XXX import * 报错 但是 XXX.py 确实在同一个目录下,但是无法导入XXX中的XX方法 解决问题是 : 麻烦添加 import sys sys.path.append(./)通过执行 sys.path.append(‘./’) 这行代码,您将当前目录&am…...

小程序密码显示与隐藏的实现
默认密码隐藏起来(显示为点),后面的图标是闭眼;用户点击图标后,图标变成睁眼,同时把密码明文显示出来;如此循环 Page({data: {passwordType: true, // 切换是否密码框show_pass: false // 是否…...

“亚马逊云科技创业加速器”首期聚焦AI,促进入营企业业务发展
生成式AI技术飞速发展,颠覆着人们的生活,正在掀起新一轮的科技革命。在生成式AI的浪潮中,亚马逊云科技旨在为中国的优秀初创企业提供全方位支持,助其抢占先机。 在6月底举办的亚马逊云科技中国峰会上,亚马逊云科技联合…...

已解决“SyntaxError: invalid character in identifier“报错问题
本文摘要:本文已解决 Python FileNotFoundError 的相关报错问题,并总结提出了几种可用解决方案。同时结合人工智能GPT排除可能得隐患及错误。 😎 作者介绍:我是程序员洲洲,一个热爱写作的非著名程序员。CSDN全栈优质领…...

2023-09-02力扣每日一题
链接: 2511. 最多可以摧毁的敌人城堡数目 题意和解: 阅读理解题,要从1到-1或-1到1,中间只能有0,求最多能有多少0 实际代码: #include<bits/stdc.h> using namespace std; int captureForts(vect…...

服务war包部署SpringBootServletInitializer 的作用
在 Spring Boot 应用中,如果需要将应用打包成 WAR 包并部署到外部的 Servlet 容器中,就需要使用 SpringBootServletInitializer。 使用步骤: 必须创建war项目,需要创建好web项目的目录嵌入式Tomcat依赖scope指定provided编写Spr…...
[Linux]进程程序替换
[Linux]进程程序替换 文章目录 [Linux]进程程序替换进程程序替换的意义见一见进程程序替换进程程序替换的原理进程程序替换中的写时拷贝介绍进程程序替换接口 进程程序替换的意义 Linux系统下使用fork系统函数创建子进程后,子进程只能执行继承的部分父进程代码&…...
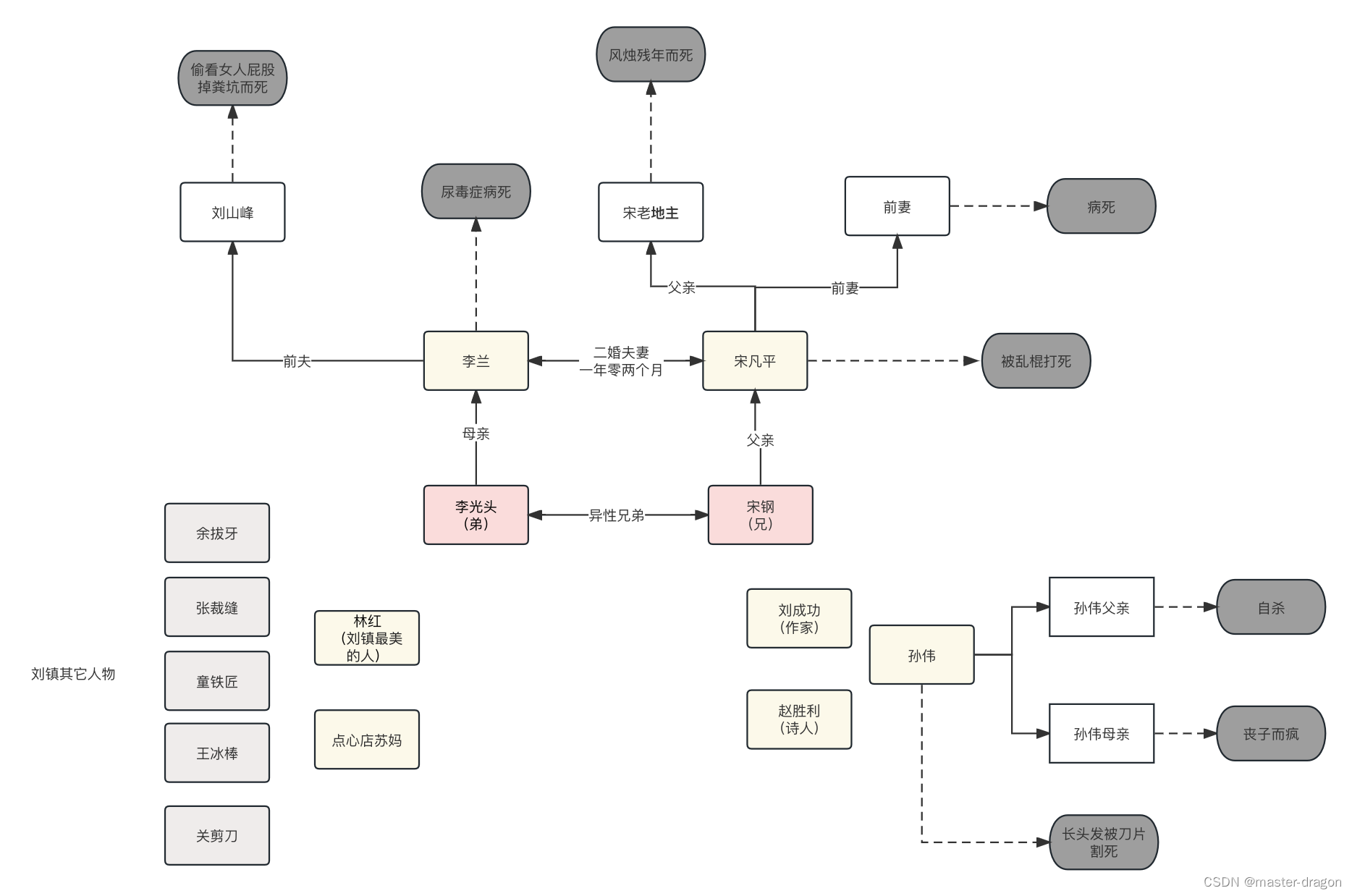
读余华小说《兄弟》
上部读完的一些笔记和思考,下部 TODO 时间:上世纪6、70年代 地点:刘镇 人物:故事中的兄弟指的是:宋钢(兄),李光头(弟),如下为简单的人物和命运图 一些故事:…...

机器学习课后习题 --回归
(一)单选题 1.以下()组变量之间存在线性回归关系? A:学生的性别与他的成绩 B:儿子的身高与父亲的身高 C:正方形的边长与面积D: 正三角形的边长与周长 2.回归问题和分类问题的区别是? A:回归问题有标签,分类问题…...
【golang】15、cobra cli 命令行库
Cobra 是 golang 最流行的命令行库,文档见 一、脚手架 mkdir pt && cd pt && go mod init cobra-cli init # 在项目下运行即可生成脚手架# tree . ├── LICENSE ├── cmd # 生成了cmd目录 │ └── root.go # 生成了root.go, 其中定义了ro…...
黑马 大事件项目 笔记
学习视频:黑马 Vue23 课程 后台数据管理系统 - 项目架构设计 在线演示:https://fe-bigevent-web.itheima.net/login 接口文档: https://apifox.com/apidoc/shared-26c67aee-0233-4d23-aab7-08448fdf95ff/api-93850835 接口根路径: http:/…...
C#2010 .NET4 解析 json 字符串
下载Newtonsoft.Json.dll using System; using System.Collections.Generic; using System.Linq; using System.Text;using Newtonsoft.Json; using Newtonsoft.Json.Linq; using System; namespace ConsoleApplication1 {class Program{static void Main(string[] args){strin…...
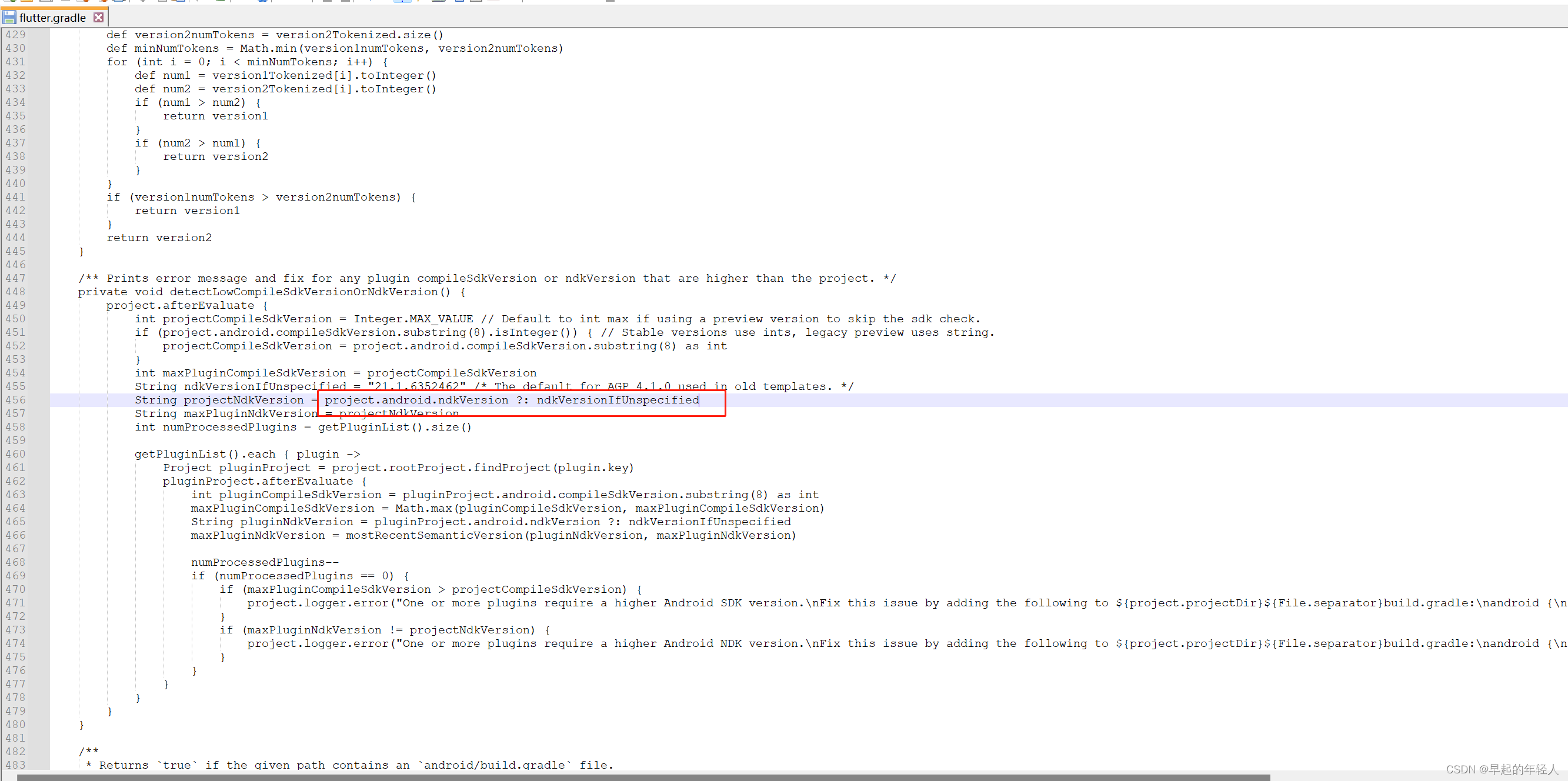
flutter Could not get unknown property ‘ndkVersion’
使用的 flutter 版本为 3.7.2 ,编译运行 如下 Could not get unknown property ‘ndkVersion’ for object of type com.android.build.gradle.internal.dsl.BaseAppModuleExtension 解决方法是 在flutter-3.7.2\packages\flutter_tools\gradle\flutter.gradle配置…...
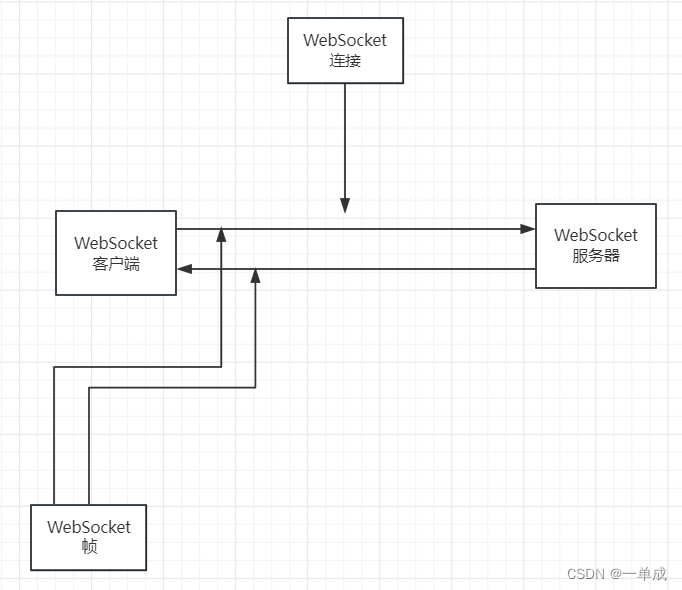
WebSocket--技术文档--架构体系--《WebSocket实现原理以及关键组件》
WebSocket产生背景 简单的说,WebSocket协议之前,双工通信是通过多个http链接来实现,这导致了效率低下。WebSocket解决了这个问题。下面是标准RFC6455中的产生背景概述。 长久以来, 创建实现客户端和用户端之间双工通讯的web app都会造成HTT…...

LeetCode-45-跳跃游戏Ⅱ-贪心算法
题目描述: 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[i] i j < n 返回到…...

商品详情接口使用 API 调用获取商品数据的完整方案
在电子商务应用程序中,商品详情接口是不可或缺的一部分。它用于从电商平台或自己的数据库中获取商品数据,并将其提供给应用程序的其他部分使用。本文将详细介绍如何设计一个完整的商品详情接口方案,其中包括使用 API 调用来获取商品数据的过程…...
vue+element-ui el-table组件二次封装实现虚拟滚动,解决数据量大渲染DOM过多而卡顿问题
一、此功能已集成到TTable组件中 二、最终效果 三、需求 某些页面不做分页时,当数据过多,会导致页面卡顿,甚至卡死 四、虚拟滚动 一、固定一个可视区域的大小并且其大小是不变的,那么要做到性能最大化就需要尽量少地渲染 DOM 元素…...

5.1 树和二叉树的定义
思维导图: 问题 为什么有树和二叉树? "树" 和 "二叉树" 都是数据结构中常用的结构,它们分别有其独特的应用和优点。我们可以从它们的定义和特性中理解为什么它们都存在。 1. **树 (Tree):** - **定义**:…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...
