机器学习课后习题 --回归
(一)单选题
1.以下()组变量之间存在线性回归关系?
A:学生的性别与他的成绩
B:儿子的身高与父亲的身高
C:正方形的边长与面积
D: 正三角形的边长与周长
2.回归问题和分类问题的区别是?
A:回归问题有标签,分类问题没有
B:回归问题输出值是离散的,分类问题输出值是连续的
C:回归问题输出值是连续的,分类问题输出值是离散的
D:回归问题与分类问题在输入属性值上要求不同
3.以下说法错误的是?
A:残差是预测值与真实值之间的差值
B:损失函数越小,模型训练得一定越好
C:正则项的目的是为了避免模型过拟合
D:最小二乘法不需要选择学习率
4.哪些算法不需要数据归一化?
A:kNN
B:k-means
C:SVM
D: 决策树
5.以下()些方法不能用于处理欠拟合?
A:增大正则化系数
B:增加新的特征
C:增加模型复杂度
D:对特征进行变换,使用组合特征或高维特征
6.以下哪些方法不能用于处理过拟合?
A:对数据进行清洗
B:增大训练数据的量
C:利用正则化技术
D:增加数据属性的复杂度
7.下列关于线性回归分析中的残差(Residuals)说法正确的是?
选项:
A:残差均值总是为零
B:残差均值总是小于零
C:残差均值总是大于零
D:以上说法都不对
8.为了观察测试 Y 与 X 之间的线性关系,X 是连续变量,使用下列哪种图形比较适合?
选项:
A:散点图
B:柱形图
C:直方图
D:以上都不对
9.假如你在训练一个线性回归模型,则:1. 如果数据量较少,容易发生过拟合。2. 如果假设空间较小,容易发生过拟合。关于这两句话,下列说法正确的是?
选项:
A:1 和 2 都错误
B:1 正确,2 错误
C:1 错误,2 正确
D:1 和 2 都正确
10.关于特征选择,下列对 Ridge 回归和 Lasso 回归说法正确的是?
选项:
A:Ridge 回归适用于特征选择
B:Lasso 回归适用于特征选择
C:两个都适用于特征选择
D:以上说法都不对
11.构建一个最简单的线性回归模型需要几个系数(只有一个特征)?
选项:
A:1 个
B:2 个
C:3 个
D:4 个
12.向量x=[1,2,3,4,-9,0]的L1范数是多少?
A:1
B:19
C:6
D:根号111
(二)多选题
1.以下哪些是使用数据规范化(特征缩放)的原因?
A:它通过降低梯度下降的每次迭代的计算成本来加速梯度下降
B:它通过减少迭代次数来获得一个好的解,从而加快了梯度下降的速度
C:它不能防止梯度下降陷入局部最优
D:它防止矩阵X^TX 不可逆(奇异/退化)
2.线性回归中,我们可以使用最小二乘法来求解系数,下列关于最小二乘法说法正确的是?( )
A:只适用于线性模型,不适合逻辑回归模型等其他模型
B:不需要选择学习率
C:当特征数量很多的时候,运算速度会很慢
D:不需要迭代训练
3.欠拟合的处理主要有哪些方式:()
A:增加模型复杂度
B:减小正则化系数
C:增大正则化系数
D:添加新特征
4.假如使用一个较复杂的回归模型来拟合样本数据,使用 Ridge回归,调试正则化参数,来降低模型复杂度,若正则化系数较大时,关于偏差(bias)和方差(variance),下列说法正确的是?( )
选项:
A:偏差减小
B:偏差增大
C:方差减小
D:方差增大
(三)判断题
1.如果两个变量相关,那么它们一定是线性关系。
答案: 【错误】
2.随机梯度下降,每次迭代时候,使用一个样本。
答案: 【正确】
3.L2正则化往往用于防止过拟合,而L1正则化往往用于特征选择。
答案: 【正确】
4.过拟合的处理可以通过减小正则化系数。
答案: 【错误】
相关文章:

机器学习课后习题 --回归
(一)单选题 1.以下()组变量之间存在线性回归关系? A:学生的性别与他的成绩 B:儿子的身高与父亲的身高 C:正方形的边长与面积D: 正三角形的边长与周长 2.回归问题和分类问题的区别是? A:回归问题有标签,分类问题…...
【golang】15、cobra cli 命令行库
Cobra 是 golang 最流行的命令行库,文档见 一、脚手架 mkdir pt && cd pt && go mod init cobra-cli init # 在项目下运行即可生成脚手架# tree . ├── LICENSE ├── cmd # 生成了cmd目录 │ └── root.go # 生成了root.go, 其中定义了ro…...
黑马 大事件项目 笔记
学习视频:黑马 Vue23 课程 后台数据管理系统 - 项目架构设计 在线演示:https://fe-bigevent-web.itheima.net/login 接口文档: https://apifox.com/apidoc/shared-26c67aee-0233-4d23-aab7-08448fdf95ff/api-93850835 接口根路径: http:/…...
C#2010 .NET4 解析 json 字符串
下载Newtonsoft.Json.dll using System; using System.Collections.Generic; using System.Linq; using System.Text;using Newtonsoft.Json; using Newtonsoft.Json.Linq; using System; namespace ConsoleApplication1 {class Program{static void Main(string[] args){strin…...
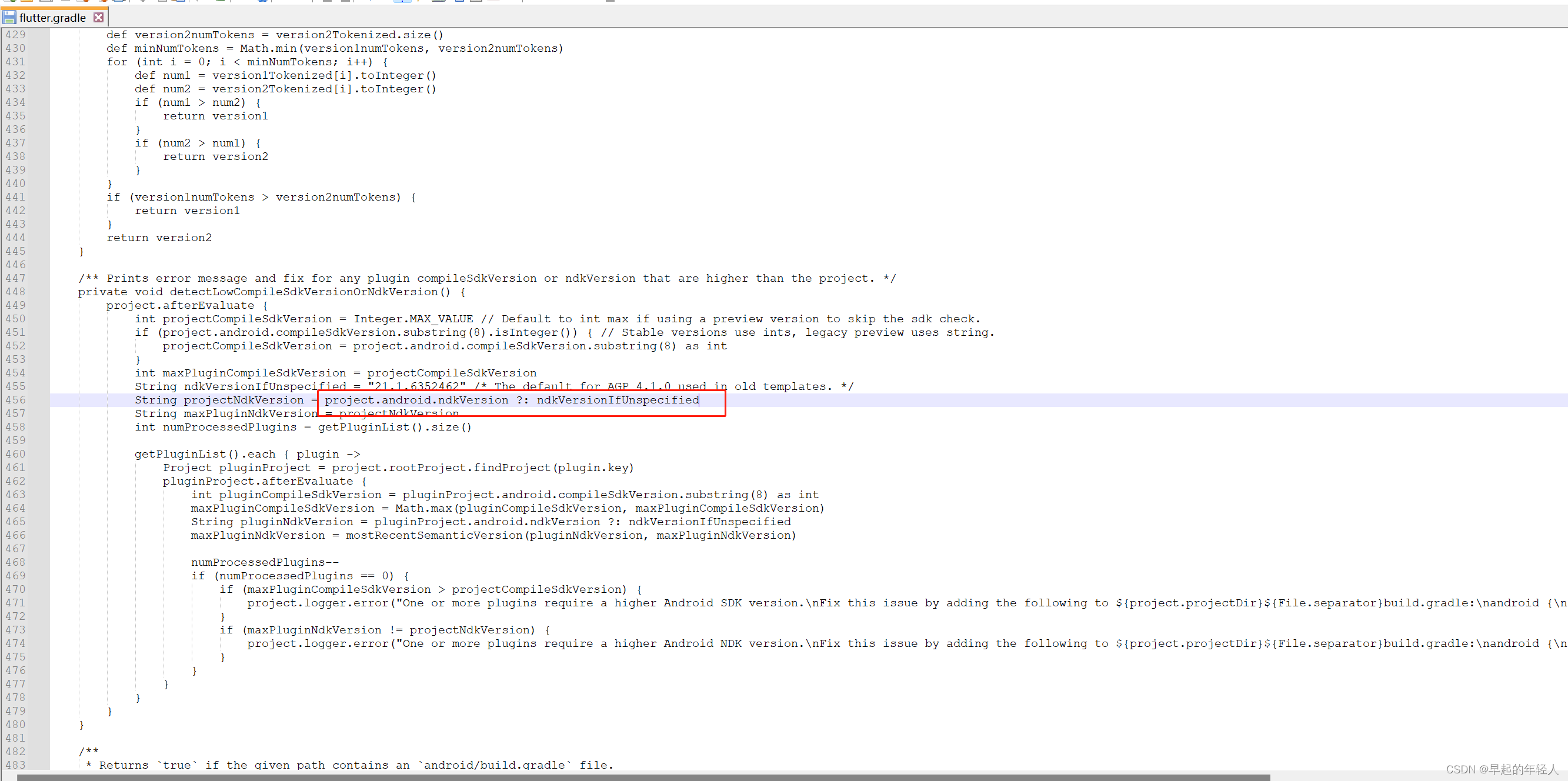
flutter Could not get unknown property ‘ndkVersion’
使用的 flutter 版本为 3.7.2 ,编译运行 如下 Could not get unknown property ‘ndkVersion’ for object of type com.android.build.gradle.internal.dsl.BaseAppModuleExtension 解决方法是 在flutter-3.7.2\packages\flutter_tools\gradle\flutter.gradle配置…...
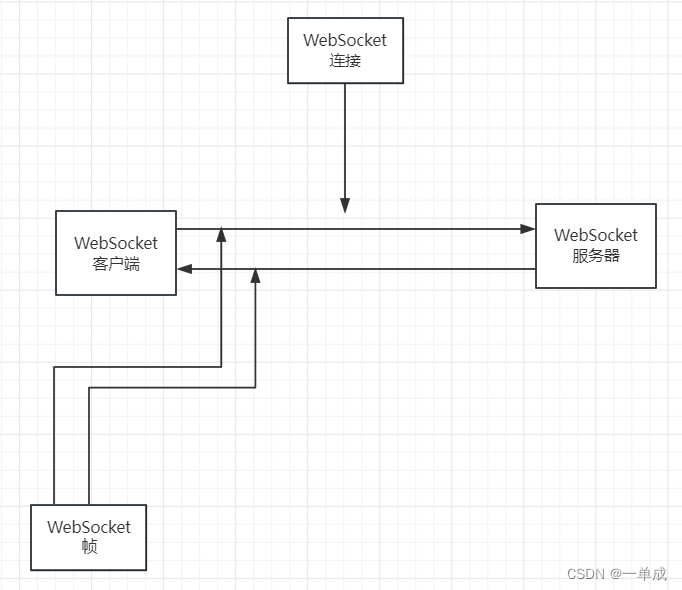
WebSocket--技术文档--架构体系--《WebSocket实现原理以及关键组件》
WebSocket产生背景 简单的说,WebSocket协议之前,双工通信是通过多个http链接来实现,这导致了效率低下。WebSocket解决了这个问题。下面是标准RFC6455中的产生背景概述。 长久以来, 创建实现客户端和用户端之间双工通讯的web app都会造成HTT…...

LeetCode-45-跳跃游戏Ⅱ-贪心算法
题目描述: 给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。 每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i j] 处: 0 < j < nums[i] i j < n 返回到…...

商品详情接口使用 API 调用获取商品数据的完整方案
在电子商务应用程序中,商品详情接口是不可或缺的一部分。它用于从电商平台或自己的数据库中获取商品数据,并将其提供给应用程序的其他部分使用。本文将详细介绍如何设计一个完整的商品详情接口方案,其中包括使用 API 调用来获取商品数据的过程…...
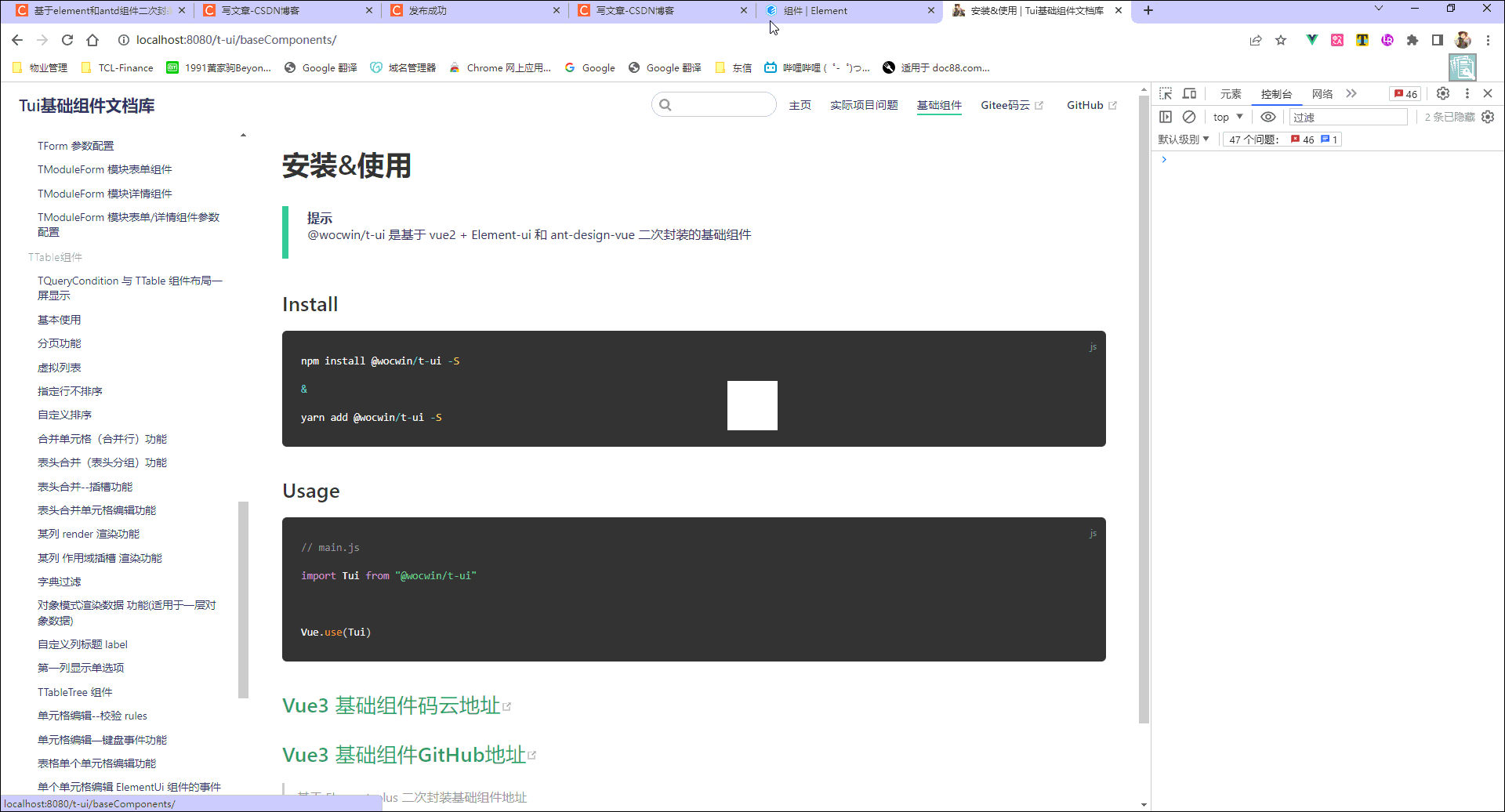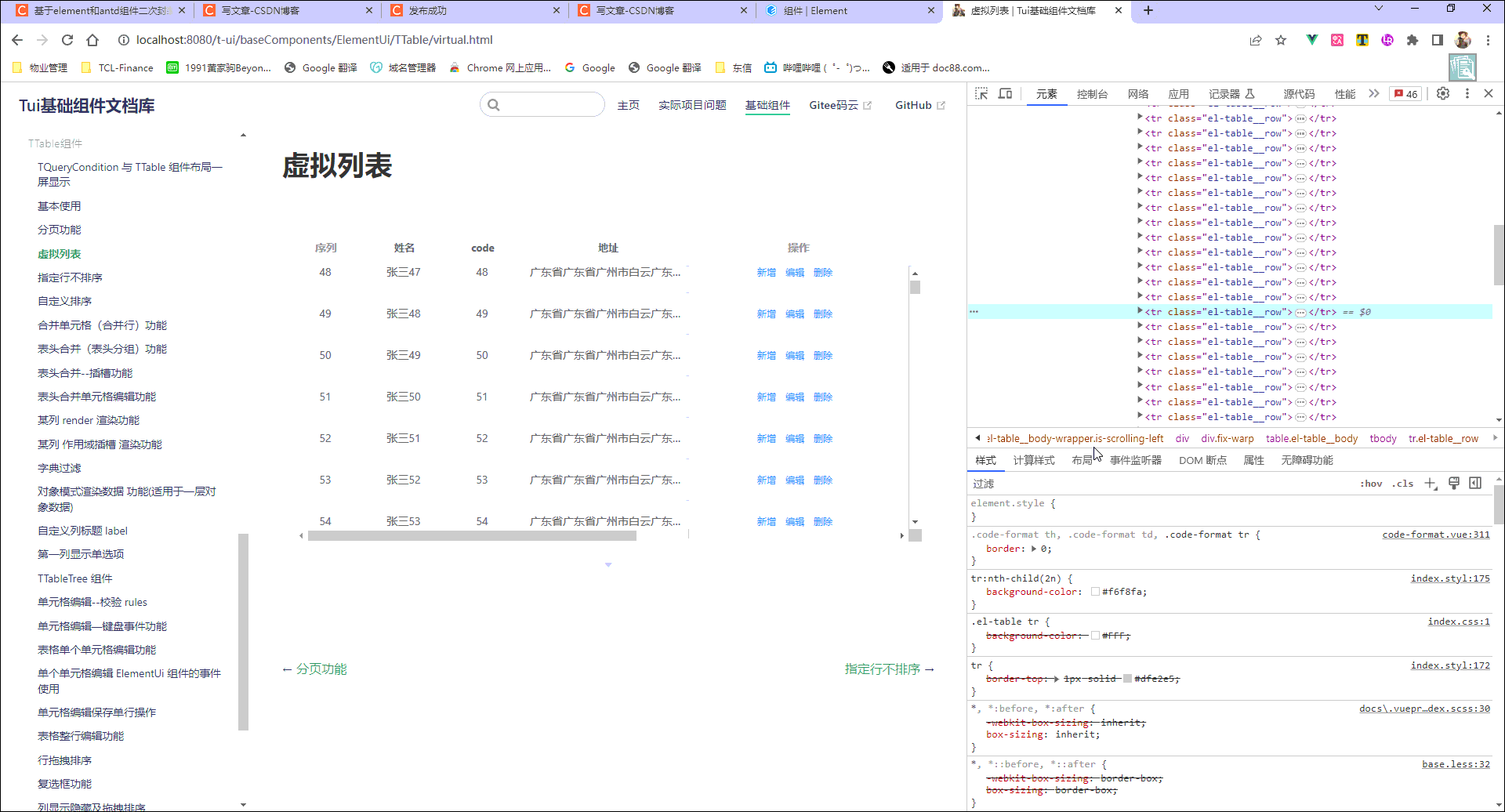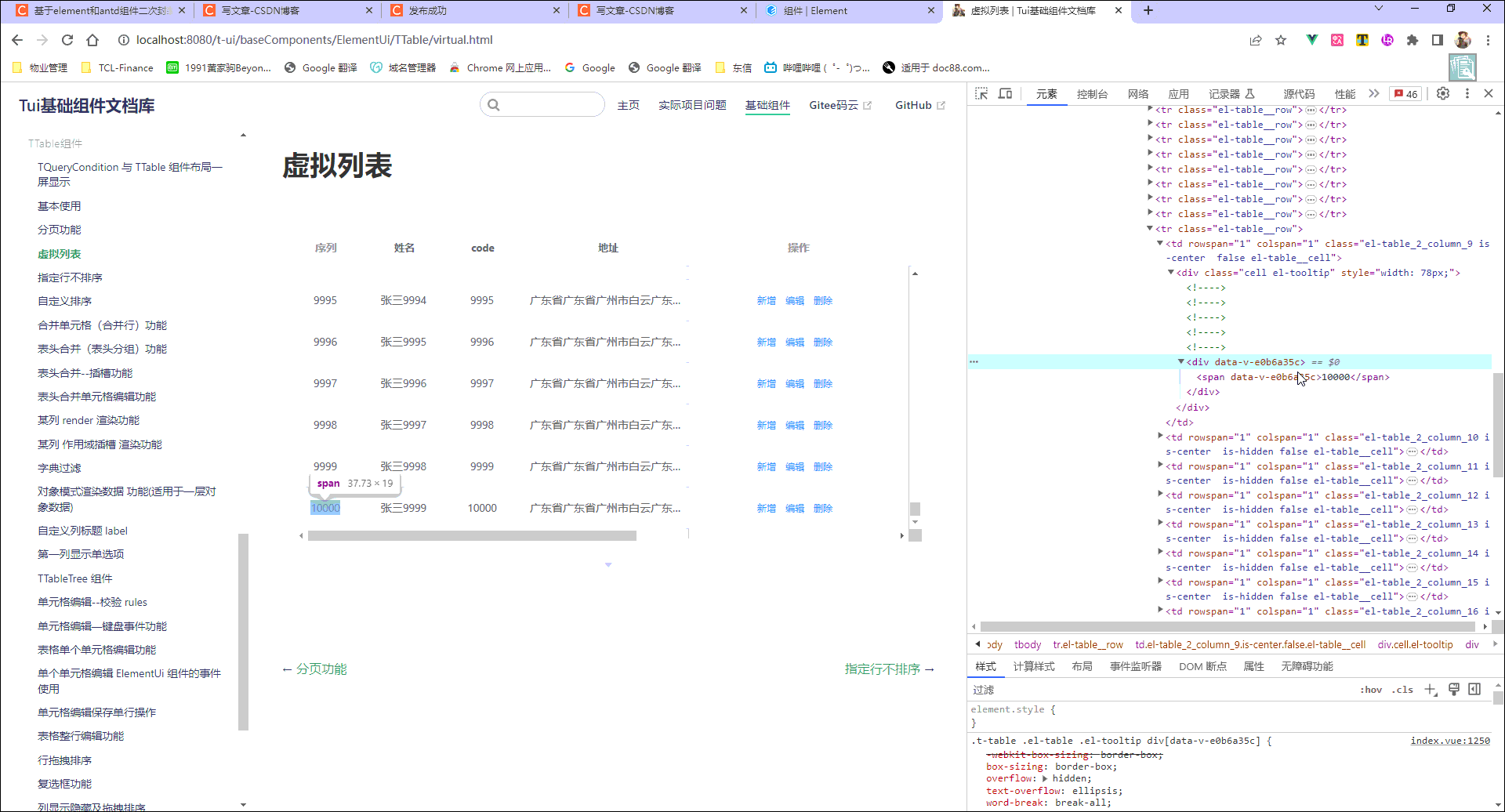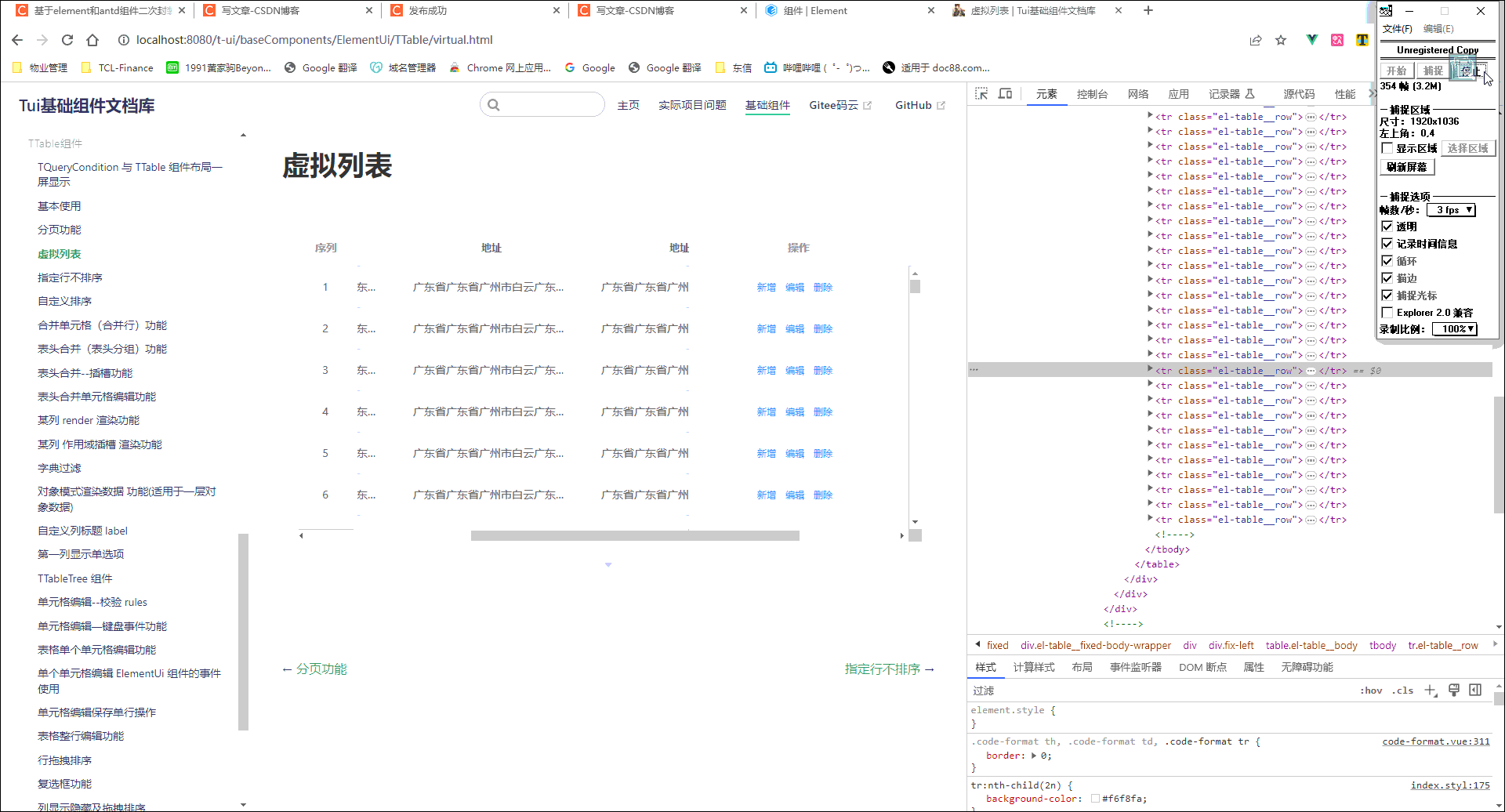
vue+element-ui el-table组件二次封装实现虚拟滚动,解决数据量大渲染DOM过多而卡顿问题
一、此功能已集成到TTable组件中 二、最终效果 三、需求 某些页面不做分页时,当数据过多,会导致页面卡顿,甚至卡死 四、虚拟滚动 一、固定一个可视区域的大小并且其大小是不变的,那么要做到性能最大化就需要尽量少地渲染 DOM 元素…...

5.1 树和二叉树的定义
思维导图: 问题 为什么有树和二叉树? "树" 和 "二叉树" 都是数据结构中常用的结构,它们分别有其独特的应用和优点。我们可以从它们的定义和特性中理解为什么它们都存在。 1. **树 (Tree):** - **定义**:…...
Java单元测试及常用语句 | 京东物流技术团队
1 前言 编写Java单元测试用例,即把一段复杂的代码拆解成一系列简单的单元测试用例,并且无需启动服务,在短时间内测试代码中的处理逻辑。写好Java单元测试用例,其实就是把“复杂问题简单化,建单问题深入化“。在编写的…...
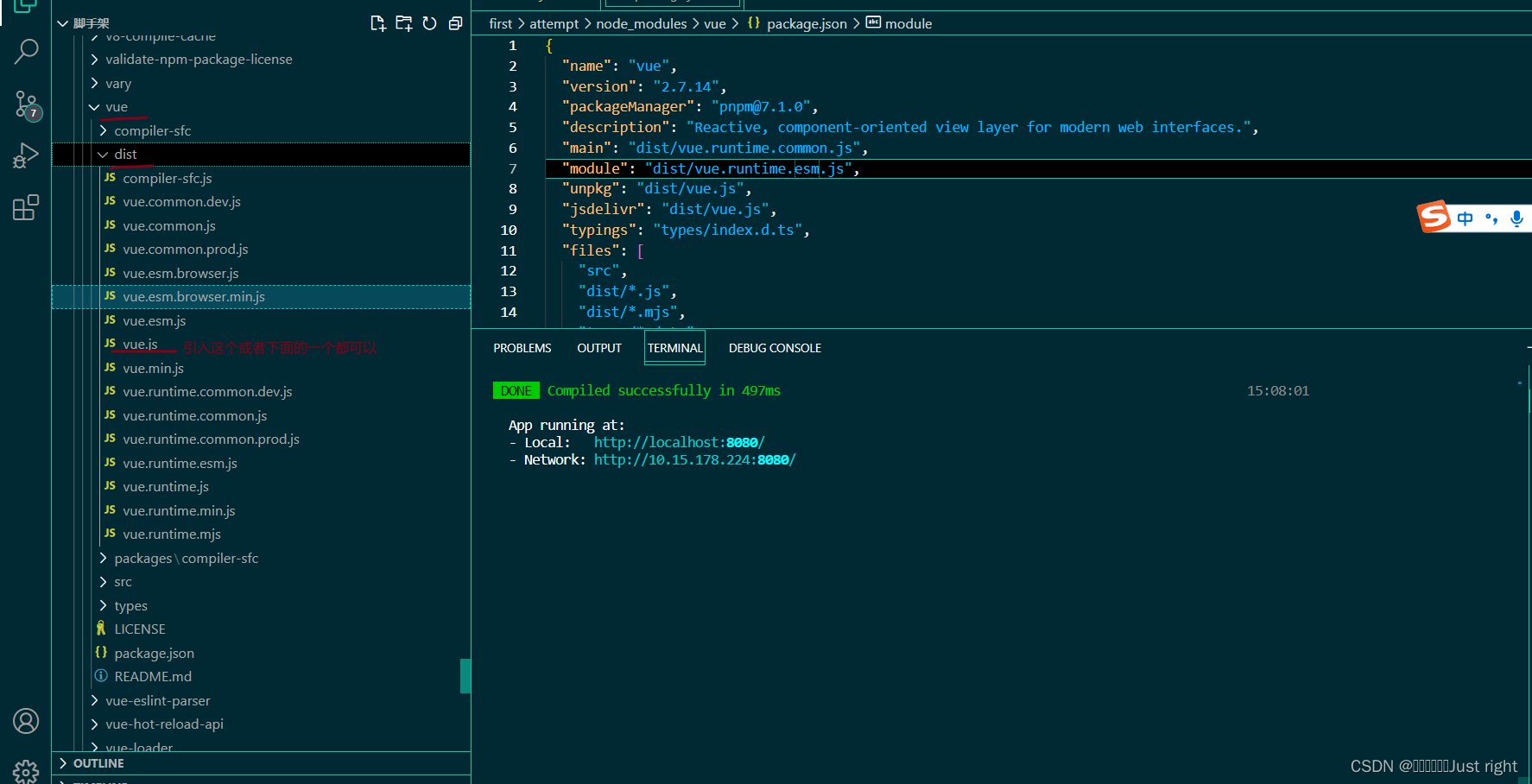
详解Vue中的render: h => h(App)
声明:只是记录,会有错误,谨慎阅读 我们用脚手架初始化工程的时候,main.js的代码如下 import Vue from vue import App from ./App.vueVue.config.productionTip falsenew Vue({// 把app组件放入容器中render: h > h(App), }).$mount(#ap…...

归并排序的详解!
本文旨在讲解归并排序的实现(递归及非递归)搬好小板凳,干货来了! 前序: 在介绍归并排序之前,需要给大家介绍的是什么是归并,归并操作,也叫归并算法,指的是将两个顺序序列…...

排盘程序算法探寻举例(陆先生八字)
算法实现: 1.庚生未月,燥土不能生金,日支申金为日主墙根,月干辛金比劫透出傍身,月干强。年干甲木自做寅木强根,又得月支乙木中气,甲木强旺有力,时干丙火七杀得未土余气,…...

考研408 | 【操作系统】终章
I/O设备的基本概念和分类 I/O设备: I/O设备的分类 1.按使用特性: 2.按传输速率分类: 3.按信息交换的单位分类: 总结: I/O控制器 I/O设备的机械部件: I/O设备的电子部件(I/O控制器&#…...
亚马逊云科技生成式AI技术辅助教学领域,近实时智能应答2D数字人搭建
早在大语言模型如GPT-3.5等的兴起和被日渐广泛的采用之前,教育行业已经在AI辅助教学领域有过各种各样的尝试。在教育行业,人工智能技术的采用帮助教育行业更好地实现教学目标,提高教学质量、学习效率、学习体验、学习成果。例如,人…...

Programming abstractions in C阅读笔记:p139-p143
《Programming Abstractions In C》学习第55天,p139-p140,总结如下: 一、技术总结 1.文件I/O操作 文件I/O操作可以分为一下这些步骤: (1)声明文件指针对象。 File *infile;(2)打开文件 fopen()。打开文件的模式有“r”, “w…...
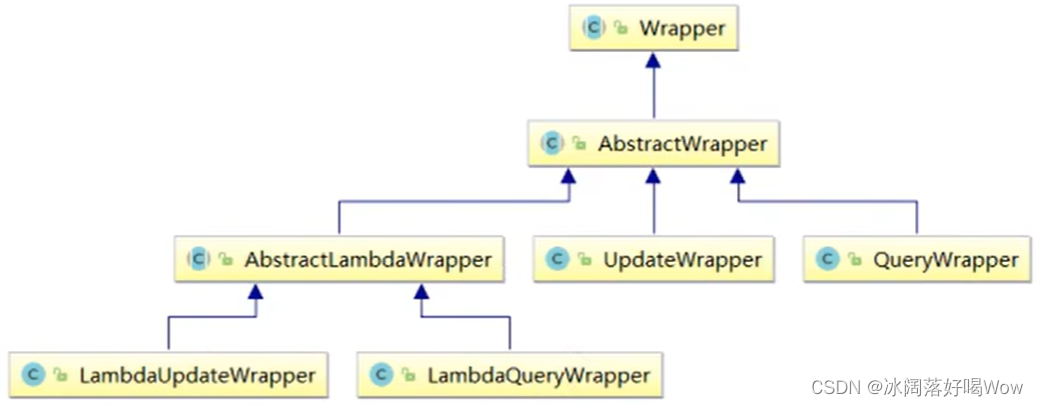
MyBatis-Plus学习笔记
1.MyBatis-Plus简介: MyBatis-Plus是一个MyBatis的增强工具,在MyBatis的基础上只做增强不做改变,为简化开发、提高效率而生。MyBatis-Plus提供了通用的mapper和service,可以在不编写任何SQL语句的情况下,快速的实现对单…...
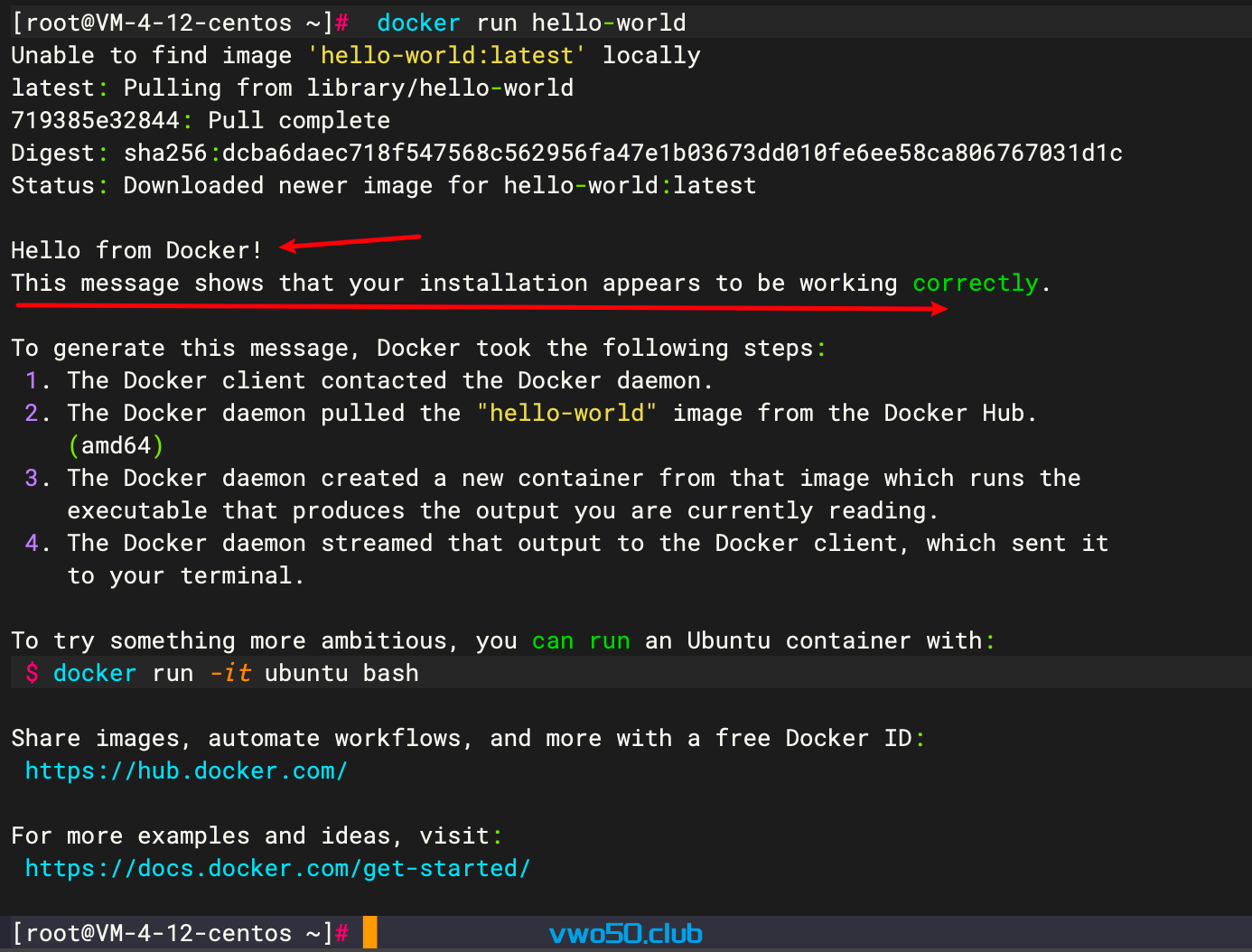
linux安装docker全过程
3. 第二步:设置docker的存储库。就两条命令,我们直接执行就好。 sudo yum install -y yum-utils sudo yum-config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo 4. 安装docker engine和docker-compose。 执行命…...

Spring 中存取 Bean 的相关注解
目录 一、五大类注解 1、五大类注解存储Bean对象 1.1Controller(控制器储存) 1.2Service(服务存储) 1.3Repository(仓库存储) 1.4Component(组件存储) 1.5Configuration(配置存储) 2、五大类注解小结 2.1为什么要这么多类注解 2.2 五大类注解之间的关系 二、方法注解 1.方法注…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

【HarmonyOS 5】鸿蒙中Stage模型与FA模型详解
一、前言 在HarmonyOS 5的应用开发模型中,featureAbility是旧版FA模型(Feature Ability)的用法,Stage模型已采用全新的应用架构,推荐使用组件化的上下文获取方式,而非依赖featureAbility。 FA大概是API7之…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...
Element-Plus:popconfirm与tooltip一起使用不生效?
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...

npm安装electron下载太慢,导致报错
npm安装electron下载太慢,导致报错 背景 想学习electron框架做个桌面应用,卡在了安装依赖(无语了)。。。一开始以为node版本或者npm版本太低问题,调整版本后还是报错。偶尔执行install命令后,可以开始下载…...
