Navicat使用HTTP通道服务器进行连接mysql数据库(超简单三分钟完成),centos安装nginx和php,docker安装nginx+php合并版
序言
因为数据库服务器在外网是不能直接连接访问的,但是可以访问网站,网站后台就能访问数据库,所以在此之前,访问数据库的数据是一件非常麻烦的事情,在平时和运维的交流中发现,他们会使用ssh通道进行连接访问数据库,之前并没在意这个东西,直到运维人员一直连不上内网数据库,我才开始研究起了navicat里这些连接配置的作用,直到我看到了HTTP…
准备文件:
找到你的navicat安装目录,ntunnel_mysql.php这个文件
第一种:本地安装nginx和php
yum install nginx
yum install php-fpm
在使用 yum 命令安装 php-fpm 时,它会同时安装 PHP 的相关依赖和文件。因此,如果你的系统中没有安装 PHP,运行 yum install php-fpm 会自动将 PHP 和 PHP-FPM 安装在系统中。
当你执行这个命令时,yum 包管理器会检查软件仓库,找到适用于你系统版本的 PHP-FPM 软件包,并自动解析其所需的依赖关系。如果系统中原本没有 PHP,yum 会自动安装 PHP 及其相关组件,以满足 PHP-FPM 的运行需求。
PHP-FPM(FastCGI Process Manager)是一个用于管理 PHP FastCGI 进程的工具。它是在 PHP 5.3.3 版本引入的一种替代方式,用于处理 PHP 的动态请求。
PHP-FPM 的主要功能包括:
-
进程管理:PHP-FPM 可以管理多个 PHP 进程,根据配置文件中的设置来控制 PHP 进程池的大小以及启动、停止和重启 PHP 进程。
-
性能调优:PHP-FPM 提供了许多配置选项,可以根据服务器的硬件和负载情况进行性能调优,如调整 PHP 进程的最大数量、最小空闲进程数量、请求超时时间等。
-
进程隔离:每个 PHP-FPM 进程都是独立的,一个进程异常退出不会影响其他进程的正常运行。同时还支持进程池隔离,即为不同用户或网站分配独立的进程池,增加安全性和稳定性。
-
统计和日志:PHP-FPM 支持记录各种统计信息和日志,包括请求处理时间、请求次数、错误日志等,方便进行监控和故障排查。
-
动态扩展:PHP-FPM 可以根据实际需要自动增加或减少 PHP 进程数量,动态适应负载变化,提高资源利用率和响应能力。
总的来说,PHP-FPM 提供了更加灵活和效率的 PHP 进程管理方式,可以提高 PHP 网站的性能和稳定性。它通常与 Nginx、Apache 等 Web 服务器配合使用,通过 FastCGI 协议进行通信,处理 PHP 脚本的执行和动态请求。
安装完成后,执行下列命令查看是否运行成功:
systemctl status nginx
systemctl status php-fpm

编辑nginx配置文件:
vim /etc/nginx/nginx.conf
# 添加如下配置
location ~ \.php$
{root /usr/share/nginx/html;include fastcgi_params;fastcgi_pass 127.0.0.1:9000;fastcgi_index index.php;fastcgi_param SCRIPT_FILENAME /usr/share/nginx/html$fastcgi_script_name;
}
创建index.php文件:
vim /usr/share/nginx/html/index.php
# 输入以下代码
<?php
phpinfo();
?>
重启nginx:
systemctl restart nginx
访问测试:
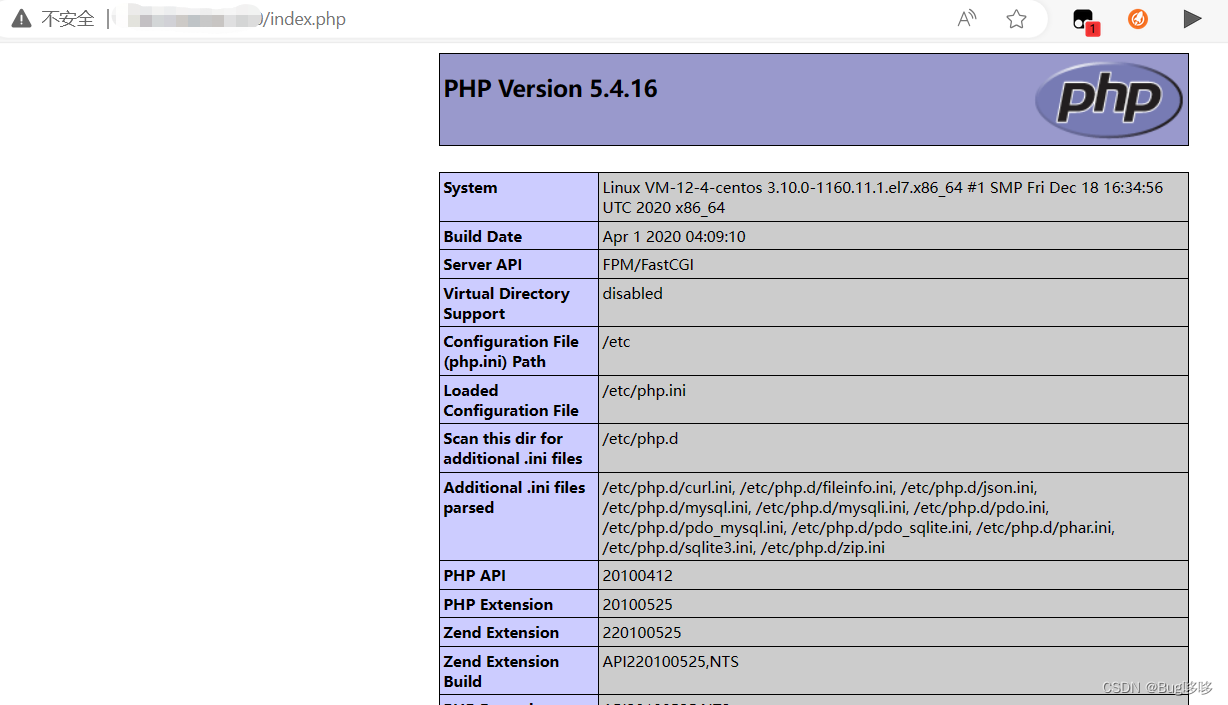
把上面准备好的ntunnel_mysql.php上传到/usr/share/nginx/html/目录
访问页面:
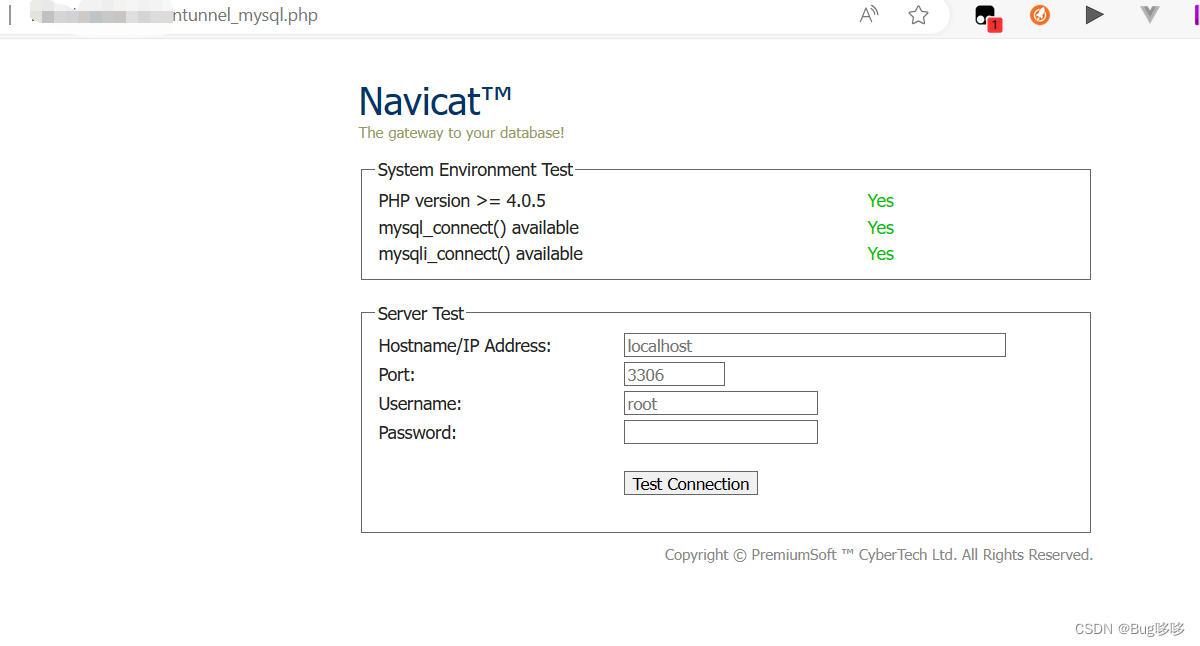
mysql_connect() available如果是no也不影响,如果不行试试
yum install php-mysql
在页面填写你的数据库信息即可连接成功。
最后在navicat里连接测试即可:
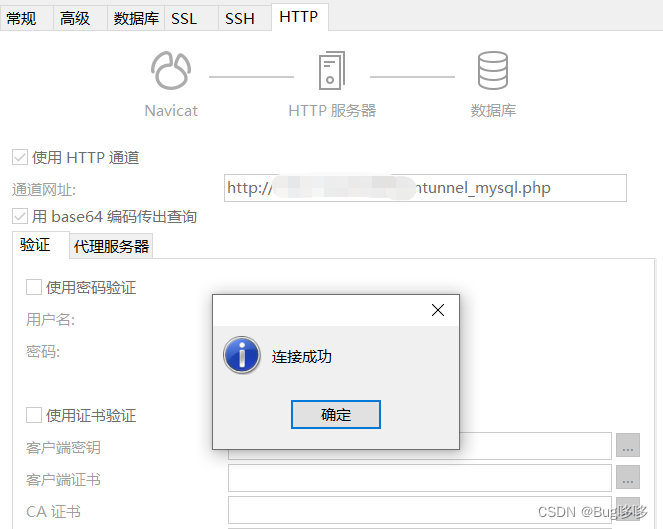
第二种:docker安装nginx+php合并版
直接上脚本:
docker rm -f php-nginx3380docker run -d --name php-nginx3380 -p 3380:80 --restart=always --privileged=true -v /docker_data/php-nginx3380/app:/app -v /etc/localtime:/etc/localtime:ro -e TZ=Asia/Shanghai webdevops/php-nginxdocker logs -f php-nginx3380
把上面准备好的ntunnel_mysql.php上传到/docker_data/php-nginx3380/app目录
访问页面,这里我的mysql_connect() available是no,但是也不影响,就不深究了:
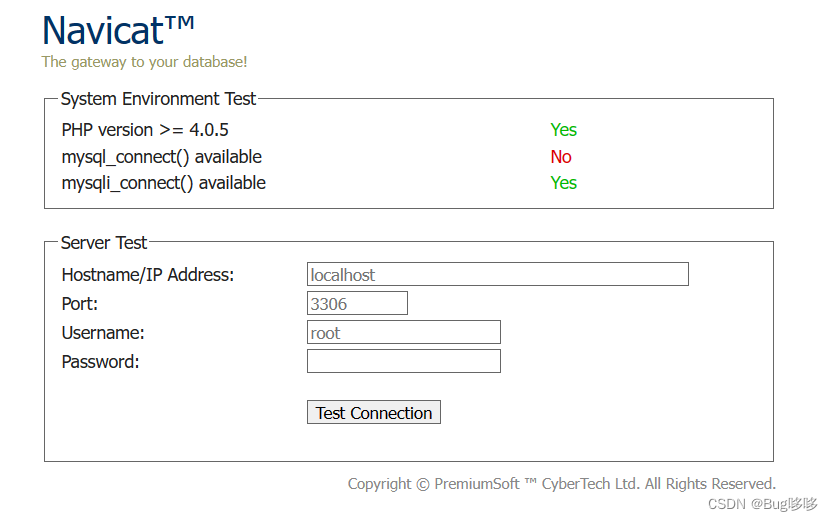
最后在navicat里连接测试即可:

至此,我们得到了 只要网站服务器能连接到的数据库,我们就能连接到该数据库 的能力。
😀😀😀
相关文章:

Navicat使用HTTP通道服务器进行连接mysql数据库(超简单三分钟完成),centos安装nginx和php,docker安装nginx+php合并版
序言 因为数据库服务器在外网是不能直接连接访问的,但是可以访问网站,网站后台就能访问数据库,所以在此之前,访问数据库的数据是一件非常麻烦的事情,在平时和运维的交流中发现,他们会使用ssh通道进行连接访…...
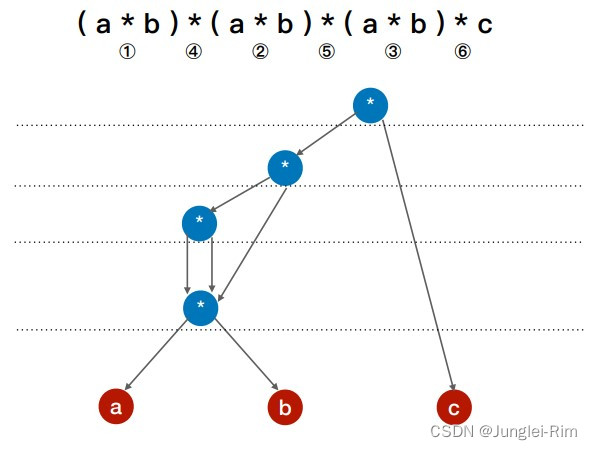
图:有向无环图(DAG)
1.有向无环图的定义 有向无环图:若一个有向图中不存在环,则称为有向无环图。 简称DAG图(Directed Acyclic Graph) 顶点中不可能出现重复的操作数。 2.有向无环图的应用 1.描述算数表达式 用有向无环图描述算术表达式。 解题步骤: 把各个操作数不重…...
Python入门教程 - 基本语法 (一)
目录 一、注释 二、Python的六种数据类型 三、字符串、数字 控制台输出练习 四、变量及基本运算 五、type()语句查看数据的类型 六、字符串的3种不同定义方式 七、数据类型之间的转换 八、标识符命名规则规范 九、算数运算符 十、赋值运算符 十一、字符串扩展 11.1…...
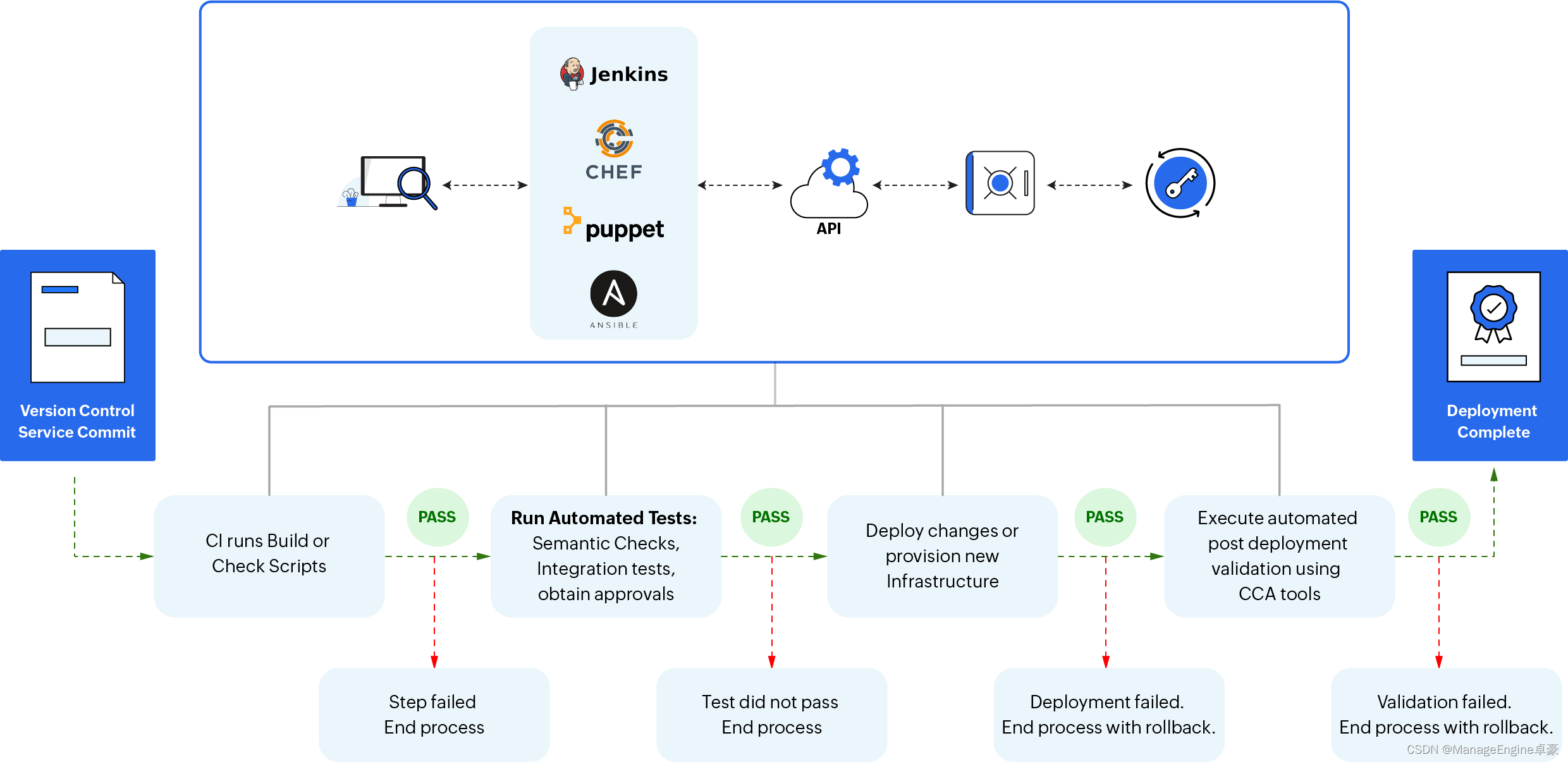
使用PAM保障开发运营安全
硬编码凭据和 DevOps 系统中缺乏凭据安全性是组织的巨大漏洞。以明文形式访问凭据的恶意内部人员可以在 IT 中建立和扩展其立足点 基础设施,构成巨大的数据被盗风险。 什么是PAM 特权访问管理 (PAM) 是指一组 IT 安全管理原则,可…...
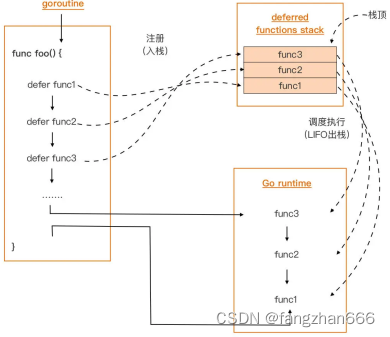
《Go 语言第一课》课程学习笔记(十二)
函数 Go 函数与函数声明 在 Go 语言中,函数是唯一一种基于特定输入,实现特定任务并可返回任务执行结果的代码块(Go 语言中的方法本质上也是函数)。在 Go 中,我们定义一个函数的最常用方式就是使用函数声明。 第一部…...

【深入浅出C#】章节10: 最佳实践和性能优化:编码规范和代码风格
编码规范和代码风格之所以重要,是因为它们直接影响到软件开发的质量、可维护性、可读性和协作效率。编码规范和代码风格是编程中的关键要素,它们有助于编写高质量、可维护和易读的代码,提高团队协作效率,减少错误,降低…...
LNMP架构:搭建Discuz论坛
文章目录 1. 编译安装Nginx1.1 前置准备1.2 编译安装1.3 添加nginx系统服务 2.编译安装MySql2.1 前置准备2.2 编译安装2.3 修改mysql 配置文件2.4 设置路径环境变量2.5 初始化数据库2.6 添加musql系统服务2.7 修改MySql登录密码 3. 编译安装PHP3.1 前置准备3.2 编译安装3.3 复制…...
)
详解Numpy(基于jupyter notebook)
详解Numpy(基于jupyter notebook) 1.创建数组2.数据类型3.数组切片和索引4.Numpy的广播与数组操作5.数组合并与通用函数6.其他通用函数 1.创建数组 #引入numpy包,以后np就代表numpy import numpy as npanp.arange(10,30,2)#10为起点…...

nvm集合node版本,解决新版本jeecgboot3.5.3前端启动失败问题
jeecgboot前端3.5.3页面如下 使用之前的pnpm启动会报错,pnpm是node进行安装的,查询后发现,vue3版本的页面至少需要node16版本,我之前的版本只有15.5,适用于vue2 那么我将先前的node15.5版本删除,然后安装…...
Windows命令行初步:更改配色、提示符以及编码方式
文章目录 启动和退出窗口标题和提示符命令行颜色更改编码 启动和退出 按下winR,调出运行窗口,输入cmd就可以进入命令行了。在Win10以前的系统种,如果在命令行中再输入一个cmd,就会再打开一个命令行。但最近的Win11版本中…...

uniapp onLoad生命周期 uni.$on接受参数无法改变data数据解决办法
问题阐述: a: uni.$emit(name,data)uni.navigateTo({url:b})b:onload(){ uni.$on(name,(res)>{ this.nameres console.log(this.name) })}用以上写法来跨页面传参会发现在b页面,虽然能够接受到参数但是赋值到data时候没生效,虽然控制台能…...
:USB/UVC Camera的使用)
Android Camera开发入门(4):USB/UVC Camera的使用
Android Camera开发入门(4):USB/UVC Camera的使用 本文基于开源项目https://github.com/saki4510t/UVCCamera之上进行二次封装和使用 在前几篇文章中,我们介绍了Camera到CameraX的基础功能应用,同时附上了相关代码,需要的源码的大佬们可以滑到最底部获取。 本篇我们一起…...
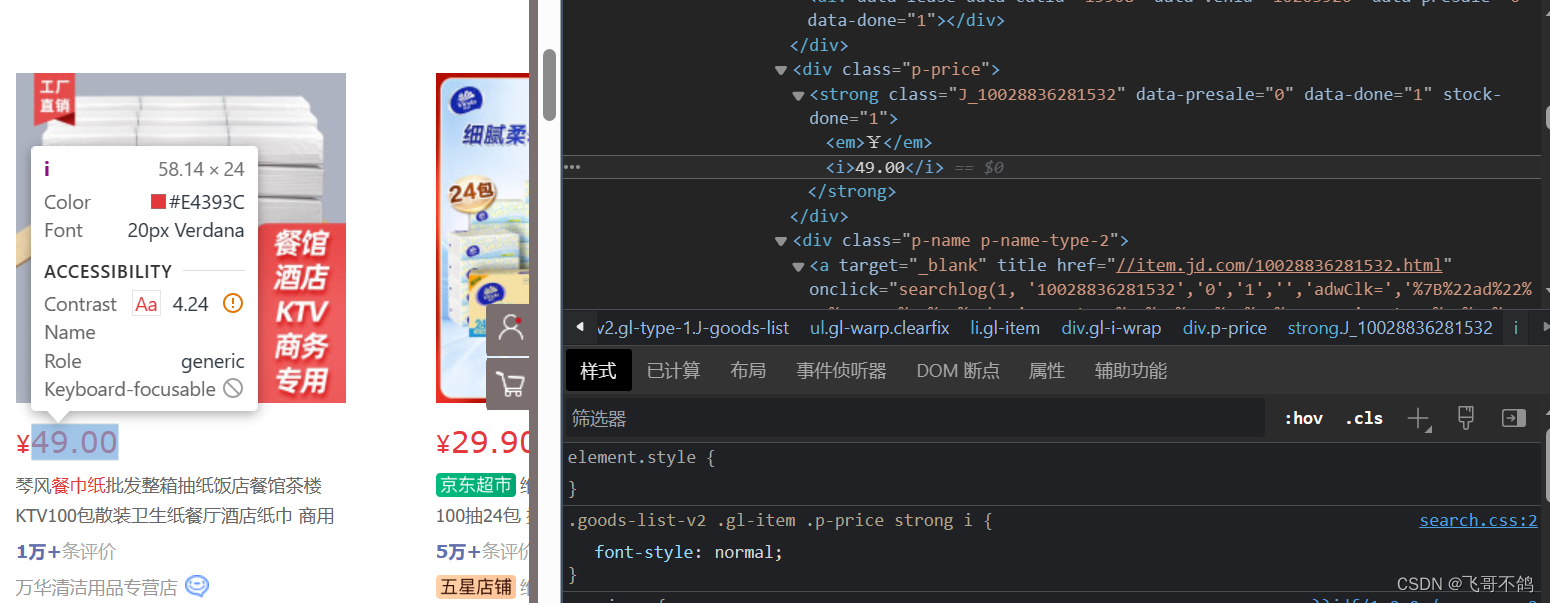
Java网络爬虫——jsoup快速上手,爬取京东数据。同时解决‘京东安全’防爬问题
文章目录 介绍jsoup使用1.解析url,获取前端代码2.解决京东安全界面跳转3.获取每一组的数据4.获取商品数据的具体信息4.最终代码 介绍 网络爬虫,就是在浏览器上,代替人类爬取数据,Java网络爬虫就是通过Java编写爬虫代码࿰…...
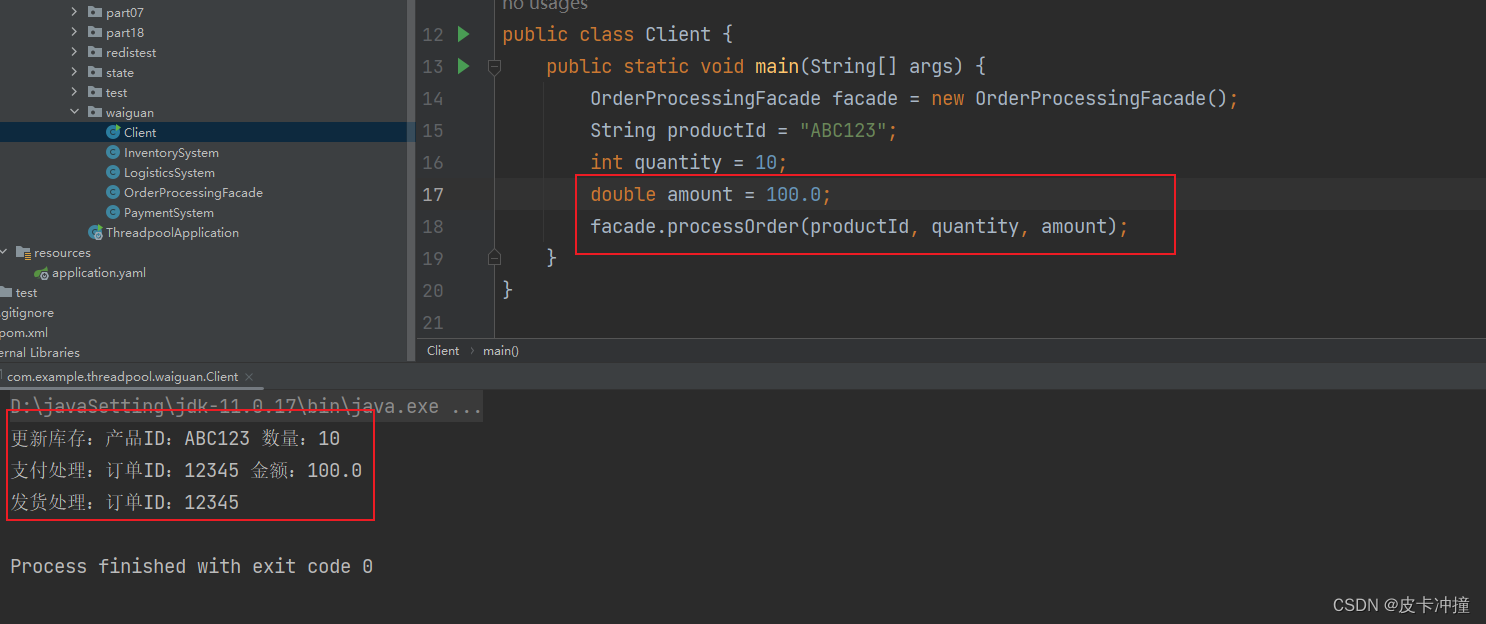
外观模式:简化复杂子系统的访问与使用
文章目录 1. 简介2. 外观模式的基本结构3. 外观模式的实现步骤4. 外观模式的应用与实例4.1 图形界面库的外观模式应用4.2 文件压缩与解压缩的外观模式应用4.3 订单处理系统的外观模式应用 5. 外观模式的优缺点5.1 优点5.2 缺点 6. 总结 1. 简介 外观模式是一种结构型设计模式&…...

代码随想录day38|509. 斐波那契数70. 爬楼梯746. 使用最小花费爬楼梯
509. 斐波那契数 class Solution:def fib(self, n: int) -> int:#dp含义,递推公式,dp初始化,遍历顺序,打印dpif n 0:return 0dp [0] * (n1)dp[0]0dp[1]1for i in range(2,n1):dp[i] dp[i-1] dp[i-2]return dp[n] 70. 爬楼梯…...

UE5 C++ UGameInstance 功能、作用及应用
# UE5 C UGameInstance 功能及作用 网上有很多文章介绍,例如在游戏中只有一个实例,换关卡不会丢失等。暂时省略。 # UE5 C UGameInstance 应用 ## 应用一,UE5 C UGameInstance 里监听player创建事件 UWebSocketGameInstance.h里的定义 …...

NodeJs-http模块
目录 一、概念二、请求报文的组成三、响应报文的组成四、创建http服务4.1 操作步骤4.2 注意事项 五、获取 HTTP 请求报文5.1 获取请求报文5.2 提取路径和查询字符串 六、设置 HTTP 响应报文七、MIME设置资源类型 一、概念 HTTP(hypertext transport protocol&#…...

翻译句子 前面的路是非常狭窄的 不能翻译成 the ahead of road is narrow 的原因
翻译句子 前面的路是非常狭窄的。The road ahead is very narrow. 可以将句子翻译成 “The ahead of road is narrow.”,但这个翻译可能不太符合英语的表达习惯。更常见的表达方式是 “The road ahead is narrow.”,这样更符合英语的语法和习惯用法。 …...

NTT功能与实现
NTT的基础功用与拓展功能: 1.evaluate和interpolate evaluate的本质是选择n个点(假设f(x)的度为n),计算得到其值,因此根据定义可以直接进行代入计算。为了加快计算的过程选取 w n w_n wn的幂次(DFT问题即离散傅里叶变换),使用FFT算法来加…...
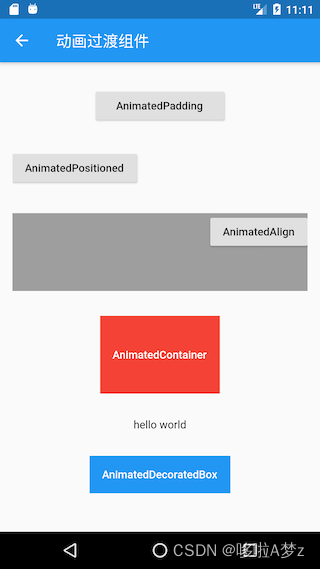
Flutter(九)Flutter动画和自定义组件
目录 1.动画简介2.动画实现和监听3. 自定义路由切换动画4. Hero动画5.交织动画6.动画切换7.Flutter预置的动画过渡组件自定义组件1.简介2.组合组件3.CustomPaint 和 RenderObject 1.动画简介 Animation、Curve、Controller、Tween这四个角色,它们一起配合来完成一个…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

提升移动端网页调试效率:WebDebugX 与常见工具组合实践
在日常移动端开发中,网页调试始终是一个高频但又极具挑战的环节。尤其在面对 iOS 与 Android 的混合技术栈、各种设备差异化行为时,开发者迫切需要一套高效、可靠且跨平台的调试方案。过去,我们或多或少使用过 Chrome DevTools、Remote Debug…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
