【算法】滑动窗口
滑动窗口应用场景
关键词:
满足xxx条件(计算结果,出现次数,同时包含)
最长/最短
子串/子数组/子序列
例如:长度最小的子数组
滑动窗使用思路(寻找最长)
核心:左右双指针(L,R)在起始点,R向右逐位滑动循环
每次滑动过程中
如果:窗内元素满足条件,R向右扩大窗口,并更新最优结果
如果:窗内元素不满足条件,L向右缩小窗口
直到R到达结尾。
例子:寻找队列里面最长的红球数量
首先滑动右指针,发现有一个红球,更新最大的数量Max为1,然后接着右移;
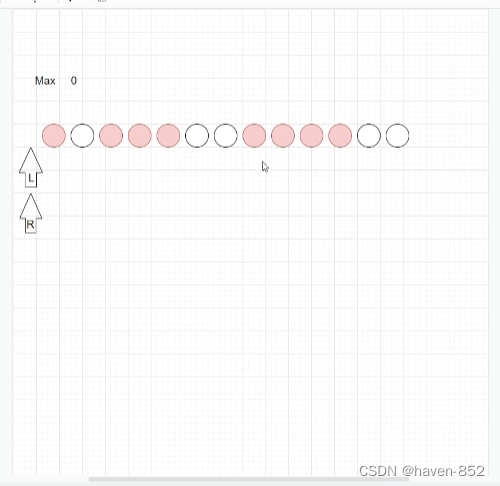
右移之后,发现没有更新最大值,那么就把左指针进行更新,左指针往右移;
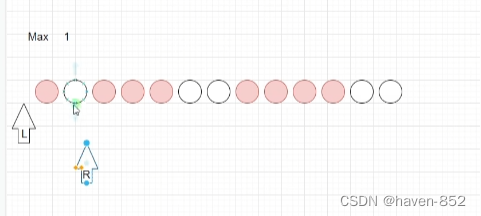
左指针右移到与右指针重复的位置,进行右指针更新;
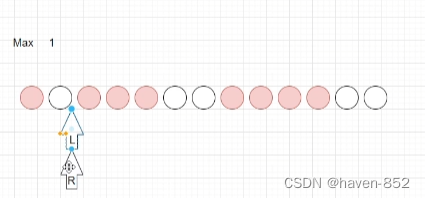
右指针接着往右移,右移的过程中发现,最大值得到更新,更新至3,一直移动到无法更新指针的为止,这时候该移动左指针;
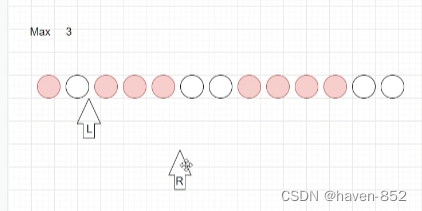
同理移动左指针到与右指针重合;
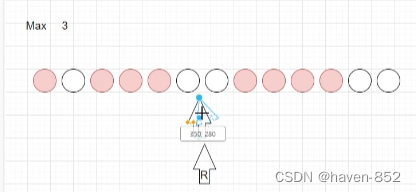
按照上述方法继续移动右指针;
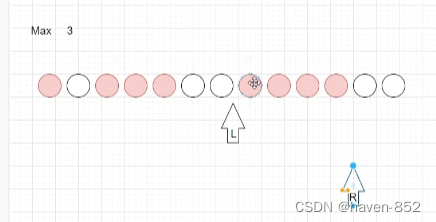
按照上述方法继续移动左指针,直至在左右指针达到最后点,循环完成。

相关文章:

【算法】滑动窗口
滑动窗口应用场景 关键词: 满足xxx条件(计算结果,出现次数,同时包含) 最长/最短 子串/子数组/子序列 例如:长度最小的子数组 滑动窗使用思路(寻找最长) 核心:左右双指…...

JS获取Beego渲染模板Temple时传递的数据
如果纯粹的JS调用接口,获取后端数据很直接坦率,JSON解析也就可以了。 如果需要JS获取HTML页面加载时,后端传回来的一些数据,我们也可以通过以下的方式进行获取。范例如下: //通过person_name字段传递参数到html页面中…...

代码随想录训练营第五十二天|300.最长递增子序列、674. 最长连续递增序列、718. 最长重复子数组
300.最长递增子序列 题目链接/文章讲解/视频讲解:代码随想录 1.代码展示 //300.最长递增子序列 int lengthOfLIS(vector<int>& nums) {if (nums.size() 1) {return 1;}//step1 构建dp数组//dp[i]的含义是长度未nums数组中长度为i 1的数组的最长子序列长…...
前端三大Css处理器之Less
Less是Css预处理器之一,分别有Sass、Less、Stylus这三个。 Lesshttps://lesscss.org/ Less是用JavaScript编写的,事实上,Less是一个JavaScript库,他通过混合、变量、嵌套和规则设置循环扩展了原生普通Css的功能。Less的少数…...
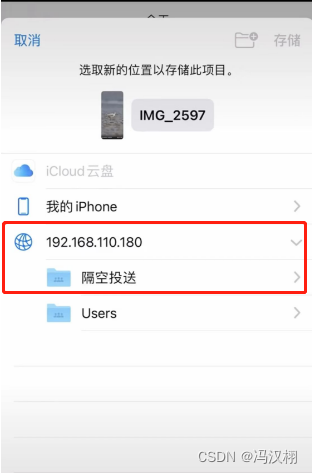
Win 教程 Win7实现隔空投送
一直觉得自己写的不是技术,而是情怀,一个个的教程是自己这一路走来的痕迹。靠专业技能的成功是最具可复制性的,希望我的这条路能让你们少走弯路,希望我能帮你们抹去知识的蒙尘,希望我能帮你们理清知识的脉络࿰…...
 | 322. 零钱兑换 | 279. 完全平方数)
代码随想录算法训练营Day45 | 70. 爬楼梯 (进阶) | 322. 零钱兑换 | 279. 完全平方数
文章目录 70. 爬楼梯 (进阶)322. 零钱兑换二维数组滚动数组 279. 完全平方数 70. 爬楼梯 (进阶) 题目链接 | 理论基础 以完全背包的思路来解题,正如组合总和 Ⅳ 中提到的一样。在本题中,先背包后物品的思路就显得非常合理明显了。 本题中的物品就是可…...
| 动态规划Part11:最长公共子序列)
算法训练营第四十一天(9.2)| 动态规划Part11:最长公共子序列
Leecode 1143.最长公共子序列 题目地址:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 题目类型:最长子序列 class Solution { public:int longestCommonSubsequence(string text1, string text2) {int m text1.size(), n t…...

k8s基于rbac权限管理serviceAccount授权管理
测试通过http访问apiServer curl没有证书不能通过https来访问apiServer需要使用kubectl代理 #使用kubectl代理 kubectl proxy --port8111& #curl访问 api/v1 是资源所属群组/版本 即创建资源时定义的apiVersion #后边跟的是要访问的资源 #查看所有命名空间 #查看核心资源用…...

linux URL访问工具
URL访问工具 有时候想在命令行下通过http访问接口/网页,可以使用curl来进行操作 发起请求 curl www.baidu.com 会返回网页内容 参数选项 -i参数 使用-i参数,会返回响应header curl -i www.baidu.com -I参数 使用-I参数,只会返回响应header cu…...

CCF-CSP 29次 第五题【202303-5 施肥】
计算机软件能力认证考试系统 题解(35分): 枚举每个区间,再枚举每个施肥车,看所有的施肥车能不能把这个区间填满 #include<bits/stdc.h> using namespace std; const int N410; int n,m; typedef pair<int,…...
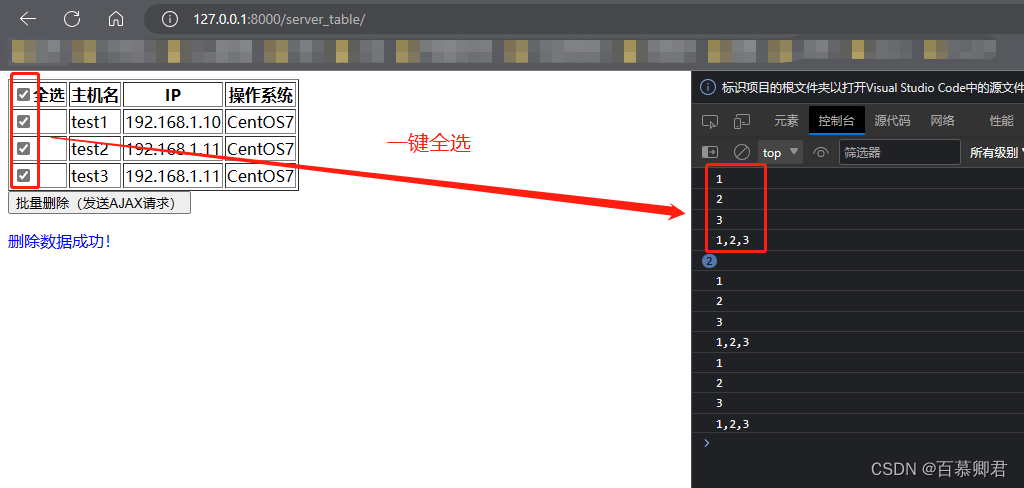
前端基础4——jQuery
文章目录 一、基本了解1.1 导入jQuery库1.2 基本语法1.3 选择器 二、操作HTML2.1 隐藏和显示元素2.2 获取与设置内容2.3 获取、设置和删除属性2.4 添加元素2.5 删除元素2.6 设置CSS样式 三、jQuery Ajax3.1 基本语法3.2 回调函数3.3 常用HTTP方法3.4 案例一3.4.1 准备工作3.4.2…...
测试人:“躺平?不可能的“, 盘点测试人在职场的优势
之前有这么一个段子:有人喜欢创造世界,他们做了程序员;有人喜欢拯救世界,他们做了测试员!近几年,测试工程师在企业究竟是怎么样的发展?随着企业对于用户体验的满意度越来越重视,更加…...

C++:初识类与this指针
文章目录 前言一、类类的定义和实例化类的访问限定符类的作用域计算类的大小 二、类的成员函数的this指针总结 个人主页 : 个人主页 个人专栏 : 《数据结构》 《C语言》《C》 前言 一、类 类的定义和实例化 注意类定义结束时后面分号( ; )不能省略。 类…...

2023应届生java面试紧张失误之一:CAS口误说成开心锁-笑坏面试官
源于:XX网,如果冒犯,表示歉意 面试官:什么是CAS 我:这个简单,开心锁 面试官:WTF? 我:一脸自信,对,就是这个 面试官:哈哈大笑ÿ…...

Excel_VBA程序文件的加密及解密说明
VBA应用技巧及疑难解答 Excel_VBA程序文件的加密及解密 在您看到这个文档的时候,请和我一起念:“唵嘛呢叭咪吽”“唵嘛呢叭咪吽”“唵嘛呢叭咪吽”,为自己所得而感恩,为付出者赞叹功德。 本不想分享之一技术,但众多学…...

Flutter关于StatefulWidget中State刷新时机的一点实用理解
刚入门flutter开发,使用StatefulWidget踩了很多坑,就我遇到典型问题谈谈见解。 1.initState方法只会在控件初始化的时候执行一遍。 2.控件内部执行setState方法,则会每次执行build方法。 3.控件销毁会执行dispose方法,所以一些…...

CS420 课程笔记 P2 - 内存编辑和基础的 GameHacking 尝试
文章目录 IntroductionOperating SystemToolsMemory ScanningMemory ScanExamples!Conclusion Introduction 本节将介绍操作系统的基础知识和内存扫描,这可以说是 game hacking 中最重要的技能,我们不会深入讨论操作系统,因为这本身就是一门…...

【sql】MongoDB 查询 高级用法
【sql】MongoDB 查询 高级用法 一、基本查询指定字段 db.getCollection(students).find({}, {name: 1, score: 1}) 二、指定字段别名 db.getCollection(students).find({}, {"name":1, "score":1, "grade":"$grade.grade"}) 这里将…...

监督学习的介绍
一、定义 监督学习是利用一组已知类别的样本调整分类器的参数,使其达到所要求性能的过程,也称为监督训练或有教师学习。它是一种机器学习的方法,目的是让模型能够从已知的输入和输出之间的关系中学习,并且能够对新的输入做出正确…...

【DRONECAN】(三)WSL2 及 ubuntu20.04 CAN 驱动安装
【DRONECAN】(三)WSL2 及 ubuntu20.04 CAN 驱动安装 前言 这一篇文章主要介绍一下 WSL2 及 ubuntu20.04 CAN 驱动的安装,首先说一下介绍本文的目的。 大家肯定都接触过 ubuntu 系统,但是我们常用的操作系统都是 Windows&#x…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

【项目实战】通过多模态+LangGraph实现PPT生成助手
PPT自动生成系统 基于LangGraph的PPT自动生成系统,可以将Markdown文档自动转换为PPT演示文稿。 功能特点 Markdown解析:自动解析Markdown文档结构PPT模板分析:分析PPT模板的布局和风格智能布局决策:匹配内容与合适的PPT布局自动…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...
