java八股文面试[数据库]——B树和B+树的区别

B树是一种树状数据结构,它能够存储数据、对其进行排序并允许以O(logn)的时间复杂度进行查找、顺序读取、插入和删除等操作。
1、B树的特性
B树中允许一个结点中包含多个key,可以是3个、4个、5个甚至更多,并不确定,需要看具体的实现。现在我们选 择一个参数M,来构造一个B树,我们可以把它称作是M阶的B树,那么该树会具有如下特点:
- 每个结点最多有M-1个key,并且以升序排列;
- 每个结点最多能有M个子结点;
- 根结点至少有两个子结点;

在实际应用中B树的阶数一般都比较大(通常大于100),所以,即使存储大量的数据,B树的高度仍然比较小,这 样在某些应用场景下,就可以体现出它的优势。
2、B树存储数据
若参数M选择为5,那么每个结点最多包含4个键值对,我们以5阶B树为例,看看B树的数据存储。

3、B树在磁盘文件中的应用
在我们的程序中,不可避免的需要通过IO操作文件,而我们的文件是存储在磁盘上的。计算机操作磁盘上的文件是通过文件系统进行操作的,在文件系统中就使用到了B树这种数据结构。
3.1、磁盘
磁盘能够保存大量的数据,从GB一直到TB级,但是 他的读取速度比较慢,因为涉及到机器操作,读取速度为毫秒 级 。

磁盘由盘片构成,每个盘片有两面,又称为盘面 。盘片中央有一个可以旋转的主轴,他使得盘片以固定的旋转速率 旋转,通常是5400rpm或者是7200rpm,一个磁盘中包含了多个这样的盘片并封装在一个密封的容器内 。盘片的每个表面是由一组称为磁道同心圆组成的 ,每个磁道被划分为了一组扇区 ,每个扇区包含相等数量的数据位,通常是512个子节,扇区之间由一些间隙隔开,这些间隙中不存储数据 。
3.2、磁盘IO

磁盘用磁头来读写存储在盘片表面的位,而磁头连接到一个移动臂上,移动臂沿着盘片半径前后移动,可以将磁头 定位到任何磁道上,这称之为寻道操作。一旦定位到磁道后,盘片转动,磁道上的每个位经过磁头时,读写磁头就 可以感知到该位的值,也可以修改值。对磁盘的访问时间分为 寻道时间,旋转时间,以及传送时间。 由于存储介质的特性,磁盘本身存取就比主存慢很多,再加上机械运动耗费,因此为了提高效率,要尽量减少磁盘I/O,减少读写操作。 为了达到这个目的,磁盘往往不是严格按需读取,而是每次都会预读,即使只需要一个字节,磁盘也会从这个位置开始,顺序向后读取一定长度的数据放入内存。这样做的理论依据是计算机科学中著名的局部性原理:当一个数据被用到时,其附近的数据也通常会马上被使用。由于磁盘顺序读取的效率很高(不需要寻道时间,只需很少的旋转时间),因此预读可以提高I/O效率。
页是计算机管理存储器的逻辑块,硬件及操作系统往往将主存和磁盘存储区分割为连续的大小相等的块,每个存储 块称为一页(1024个字节或其整数倍),预读的长度一般为页的整倍数。主存和磁盘以页为单位交换数据。当程 序要读取的数据不在主存中时,会触发一个缺页异常,此时系统会向磁盘发出读盘信号,磁盘会找到数据的起始位 置并向后连续读取一页或几页载入内存中,然后异常返回,程序继续运行。
文件系统的设计者利用了磁盘预读原理,将一个结点的大小设为等于一个页(1024个字节或其整数倍),这样每 个结点只需要一次I/O就可以完全载入。那么3层的B树可以容纳1024*1024*1024差不多10亿个数据,如果换成二 叉查找树,则需要30层!假定操作系统一次读取一个节点,并且根节点保留在内存中,那么B树在10亿个数据中查 找目标值,只需要小于3次硬盘读取就可以找到目标值,但红黑树需要小于30次,因此B树大大提高了IO的操作效率。
4、B+树
B+树是对B树的一种变形树,它与B树的差异在于:
1. 非叶结点仅具有索引作用,也就是说,非叶子结点只存储key,不存储value;
2. 树的所有叶结点构成一个有序链表,可以按照key排序的次序遍历全部数据。
4.1 B+树存储数据
若参数M选择为5,那么每个结点最多包含4个键值对,我们以5阶B+树为例,看看B+树的数据存储。
4.2 B+树和B树的对比
B+ 树的优点在于:
1.由于B+树在非叶子结点上不包含真正的数据,只当做索引使用,因此在内存相同的情况下,能够存放更多的key。 2.B+树的叶子结点都是相连的,因此对整棵树的遍历只需要一次线性遍历叶子结点即可。而且由于数据顺序排列并且相连,所以便于区间查找和搜索。而B树则需要进行每一层的递归遍历。
B树的优点在于:
由于B树的每一个节点都包含key和value,因此我们根据key查找value时,只需要找到key所在的位置,就能找到 value,但B+树只有叶子结点存储数据,索引每一次查找,都必须一次一次,一直找到树的最大深度处,也就是叶 子结点的深度,才能找到value。
B+树在数据库中的应用
在数据库的操作中,查询操作可以说是最频繁的一种操作,因此在设计数据库时,必须要考虑到查询的效率问题, 在很多数据库中,都是用到了B+树来提高查询的效率;
在操作数据库时,我们为了提高查询效率,可以基于某张表的某个字段建立索引,就可以提高查询效率,那其实这 个索引就是B+树这种数据结构实现的。
B-树深入
B树由来:
定义:B-树是一类树,包括B-树、B+树、B*树等,是一棵自平衡的搜索树,它类似普通的平衡二叉树,不同的一点是B-树允许每个节点有更多的子节点。
B-树是专门为外部存储器设计的,如磁盘,它对于读取和写入大块数据有良好的性能,所以一般被用在文件系统及数据库中。
定义只需要知道B-树允许每个节点有更多的子节点即可(多叉树)。子节点数量一般在上千,具体数量依赖外部存储器的特性。
先来看看为什么会出现B-树这类数据结构:
传统用来搜索的平衡二叉树有很多,如 AVL 树,红黑树等。这些树在一般情况下查询性能非常好,但当数据非常大的时候它们就无能为力了。原因当数据量非常大时,内存不够用,大部分数据只能存放在磁盘上,只有需要的数据才加载到内存中。一般而言内存访问的时间约为 50 ns,而磁盘在 10 ms 左右。速度相差了近 5 个数量级,磁盘读取时间远远超过了数据在内存中比较的时间。这说明程序大部分时间会阻塞在磁盘 IO 上。那么我们如何提高程序性能?减少磁盘 IO 次数,像 AVL 树,红黑树这类平衡二叉树从设计上无法“迎合”磁盘。

上图是一颗简单的平衡二叉树,平衡二叉树是通过旋转来保持平衡的,而旋转是对整棵树的操作,若只有部分加载到内存中则无法完成旋转操作。
其次平衡二叉树的高度相对较大为 log n(底数为2),这样逻辑上很近的节点实际可能非常远,无法很好的利用磁盘预读(局部性原理),所以这类平衡二叉树在数据库和文件系统上的选择就被 pass 了。
空间局部性原理:如果一个存储器的某个位置被访问,那么将它附近的位置也会被访问。
我们从“迎合”磁盘的角度来看看B-树的设计:
索引的效率依赖与磁盘 IO 的次数,快速索引需要有效的减少磁盘 IO 次数,如何快速索引呢?索引的原理其实是不断的缩小查找范围,就如我们平时用字典查单词一样,先找首字母缩小范围,再第二个字母等等。平衡二叉树是每次将范围分割为两个区间。
为了更快,B-树每次将范围分割为多个区间,区间越多,定位数据越快越精确。那么如果节点为区间范围,每个节点就较大了。所以新建节点时,直接申请页大小的空间(磁盘存储单位是按 block 分的,一般为 512 Byte。磁盘 IO 一次读取若干个 block,我们称为一页,具体大小和操作系统有关,一般为 4 k,8 k或 16 k),计算机内存分配是按页对齐的,这样就实现了一个节点只需要一次 IO。

上图是一棵简化的B-树,多叉的好处非常明显,有效的降低了B-树的高度,为底数很大的 log n,底数大小与节点的子节点数目有关,一般一棵B-树的高度在 3 层左右。层数低,每个节点区确定的范围更精确,范围缩小的速度越快(比二叉树深层次的搜索肯定快很多)。上面说了一个节点需要进行一次 IO,那么总 IO 的次数就缩减为了 log n 次。B-树的每个节点是 n 个有序的序列(a1,a2,a3…an),并将该节点的子节点分割成 n+1 个区间来进行索引(X1< a1, a2 < X2 < a3, … , an+1 < Xn < anXn+1 > an)。
点评:B树的每个节点,都是存多个值的,不像二叉树那样,一个节点就一个值,B树把每个节点都给了一点的范围区间,区间更多的情况下,搜索也就更快了,比如:有1-100个数,二叉树一次只能分两个范围,0-50和51-100,而B树,分成4个范围 1-25, 25-50,51-75,76-100一次就能筛选走四分之三的数据。所以作为多叉树的B树是更快的
三、B-树的查找
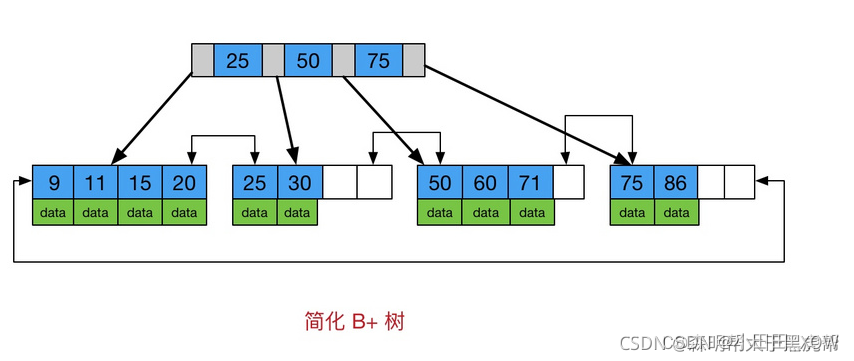
我们来看看B-树的查找,假设每个节点有 n 个 key值,被分割为 n+1 个区间,注意,每个 key 值紧跟着 data 域,这说明B-树的 key 和 data 是聚合在一起的。一般而言,根节点都在内存中,B-树以每个节点为一次磁盘 IO。
比如上图中,若搜索 key 为 25 节点的 data,首先在根节点进行二分查找(因为 keys 有序,二分最快),判断 key 25 小于 key 50,所以定位到最左侧的节点,此时进行一次磁盘 IO,将该节点从磁盘读入内存,接着继续进行上述过程,直到找到该 key 为止。
B+ 树
B+树是B-树的变体,也是一种多路搜索树, 它与 B- 树的不同之处在于:
所有关键字存储在叶子节点出现,内部节点(非叶子节点并不存储真正的 data)。
为所有叶子结点增加了一个链指针。
简化 B+树 如下图:
因为内节点并不存储 data,所以一般B+树的叶节点和内节点大小不同,而B-树的每个节点大小一般是相同的,为一页。

使用B+树的好处
由于B+树的内部节点只存放键,不存放值,因此,一次读取,可以在内存页中获取更多的键,有利于更快地缩小查找范围。
B+树的叶节点由一条链相连,因此,当需要进行一次全数据遍历的时候,B+树只需要使用O(logN)时间找到最小的一个节点,然后通过链进行O(N)的顺序遍历即可。而B树则需要对树的每一层进行遍历,这会需要更多的内存置换次数,因此也就需要花费更多的时间

知识来源:
【23版面试突击】你知道B树和B+树的区别吗?MySQL为什么使用B+树而不是B树?_哔哩哔哩_bilibili
Java数据结构算法:B树和B+树 - 知乎
B树与B+树的区别_b树和b+树的区别_森明帮大于黑虎帮的博客-CSDN博客
相关文章:

java八股文面试[数据库]——B树和B+树的区别
B树是一种树状数据结构,它能够存储数据、对其进行排序并允许以O(logn)的时间复杂度进行查找、顺序读取、插入和删除等操作。 1、B树的特性 B树中允许一个结点中包含多个key,可以是3个、4个、5个甚至更多,并不确定,需要看具体的实…...
2、Nginx 安装
文章目录 2、Nginx 安装2.1 官网下载2.2 安装 nginx2.2.1 第一步2.2.2 第二步2.2.3 第三步,安装 nginx2.2.4 第四步,修改防火漆规则 【尚硅谷】尚硅谷Nginx教程由浅入深 志不强者智不达;言不信者行不果。 2、Nginx 安装 2.1 官网下载 nginx…...

最适合 AI 的 Python Web 框架
迷途小书童的 Note 读完需要 4分钟 速读仅需 2 分钟 1 简介 本文将介绍 Gradio 库,它是 Python 的一个 web 框架,可以帮助我们快速构建交互式 AI 应用。我们将了解 Gradio 的应用场景、基本原理、功能介绍,并通过一个代码示例来演示如何使用 …...

算法通关村第十八关——回溯
回溯很大感觉就是多重递归,在递归的题目中,例如斐波那契数列,只需要考虑当前情况以及他的子情况。而在回溯中,要进行很多次递归,并且要对条件进行处理。 LeetCode257:给你一个二叉树的根节点root,按任意顺序ÿ…...
使用kafka还在依赖Zookeeper,kraft模式了解下
Kafka的Kraft模式 概述 Kafka是一种高吞吐量的分布式发布订阅消息系统,它可以处理消费者在网站中的所有动作流数据。其核心组件包含Producer、Broker、Consumer,以及依赖的Zookeeper集群。其中Zookeeper集群是Kafka用来负责集群元数据的管理、控制器…...
【100天精通Python】Day52:Python 数据分析_Numpy入门基础与数组操作
目录 1 NumPy 基础概述 1.1 NumPy的主要特点和功能 1.2 NumPy 安装和导入 2 Numpy 数组 2.1 创建NumPy数组 2.2 数组的形状和维度 2.3 数组的数据类型 2.4 访问和修改数组元素 3 数组操作 3.1 数组运算 3.2 数学函数 3.3 统计函数 4 数组形状操作 4.1 重塑数组形…...

Day01-Java基础语法
目录 1. 人机交互 1.1 什么是cmd? 1.2 如何打开CMD窗口? 1.3 常用CMD命令 1.4 CMD练习 1.5 环境变量 2. Java概述 1.1 Java是什么? 1.2下载和安装 1.2.1 下载 1.2.2 安装 1.2.3 JDK的安装目录介绍 1.3 HelloWorld小案例 2.3.1 …...

代码随想录二刷day06
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、力扣242. 有效的字母异位词二、力扣349. 两个数组的交集三、力扣202. 快乐数四、力扣1两数之和 前言 一、力扣242. 有效的字母异位词 class Solution {pub…...
可扩展的Blender插件开发汇总
成熟的 Blender 3D 插件是令人惊奇的事情。作为 Python 和 Blender 的新手,我经常发现自己被社区中的人们创造的强大的东西弄得目瞪口呆。坦率地说,其中一些包看起来有点神奇,当自我怀疑或冒名顶替综合症的唠叨声音被打破时,很容易想到“如果有人能做出可以做xxx的东西就好…...
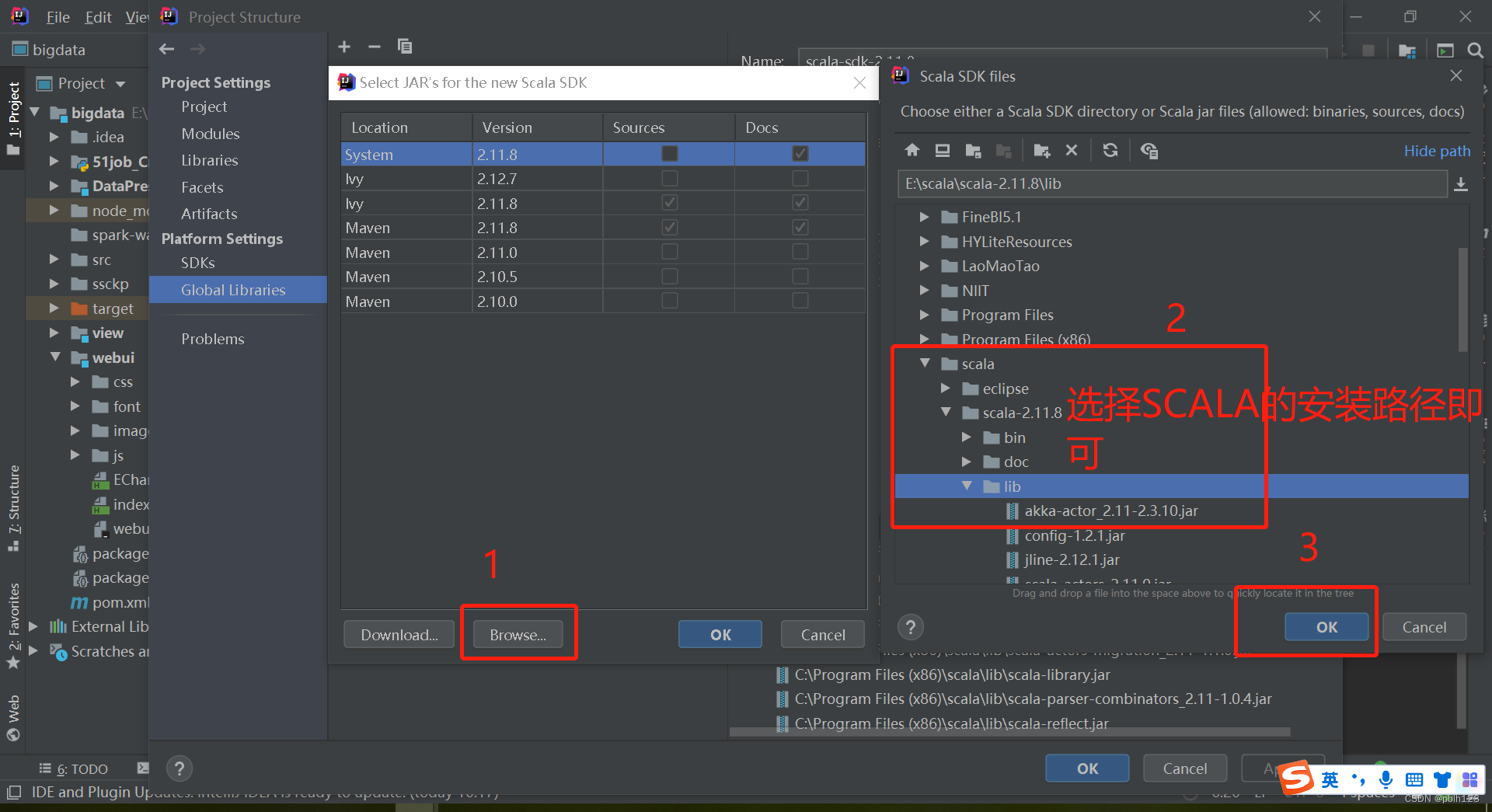
2023_Spark_实验二:IDEA安装及配置
一、下载安装包 链接:百度网盘 请输入提取码 所在文件夹:大数据必备工具--》开发工具(前端后端)--》后端 下载文件名称:ideaIU-2019.2.3.exe (喜欢新版本也可安装新版本,新旧版本会存在部分差异) IDEA …...

小赢科技,寻找金融科技核心价
如果说金融是经济的晴雨表,是通过改善供给质量以提高经济质量的切入口,那么金融科技公司,就是这一切行动的推手。上半年,社会经济活跃程度提高背后,金融科技公司既是奉献者,也是受益者。 8月29日࿰…...
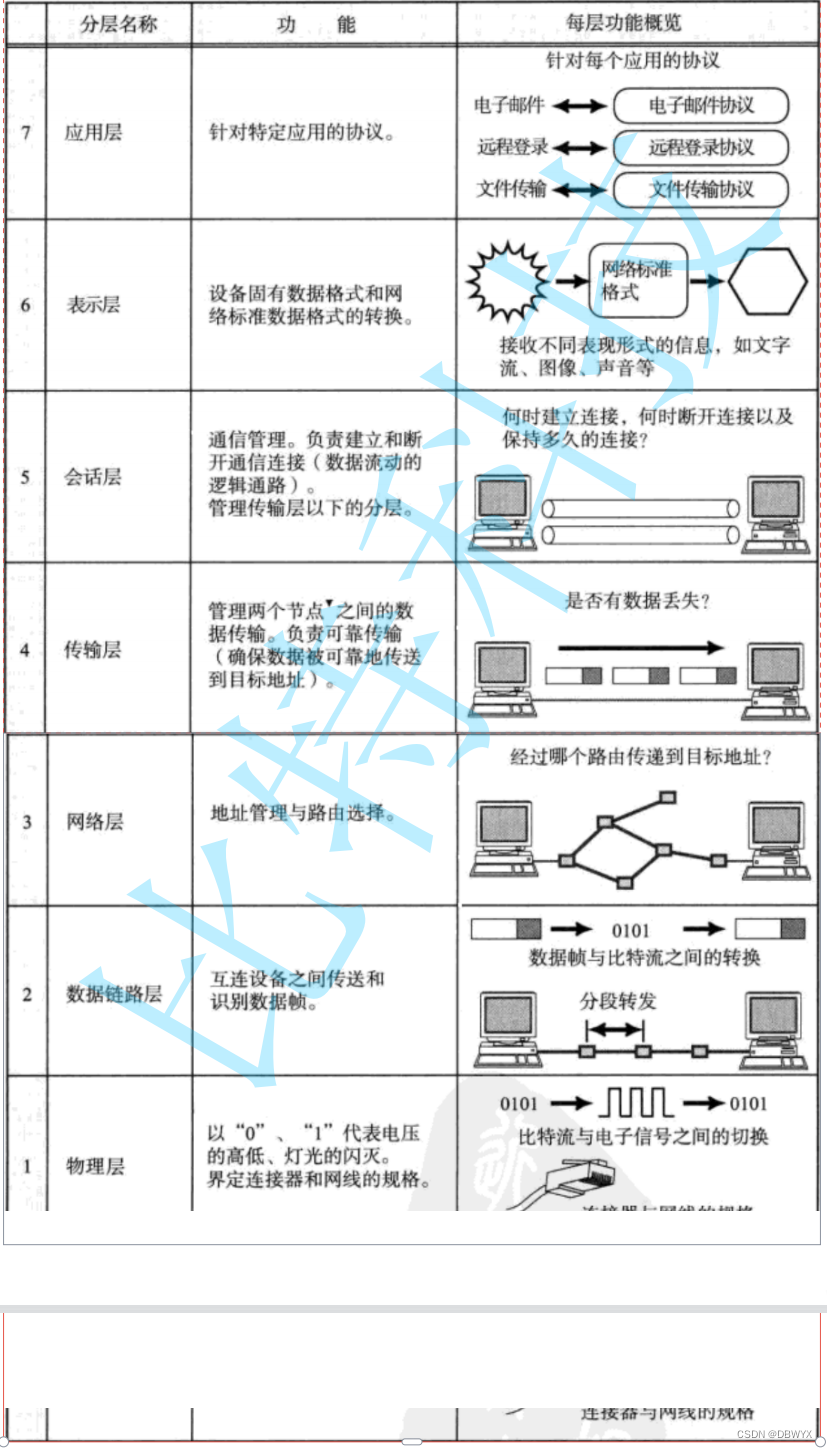
NAT与代理服务器
1.DNS Domain Name System 是一整套从域名映射到IP的系统(把域名转化为IP地址) 2.域名简介 3.周鸿祎 傅盛 4.ICMP协议 用来网络故障排查原因 草图理解“位置” ping ICMP 是绕过TCP UDP传输协议的,没有端口号 traceroute 5.NAT技术 N…...
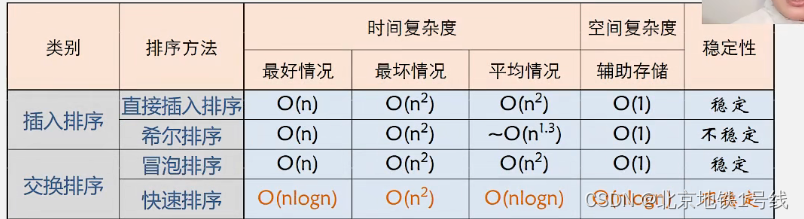
24.排序,插入排序,交换排序
目录 一. 插入排序 (1)直接插入排序 (2)折半插入排序 (3)希尔排序 二. 交换排序 (1)冒泡排序 (2)快速排序 排序:将一组杂乱无章的数据按一…...
Navicat16安装教程
注:因版权原因,本文已去除破解相关的文件和内容 1、在本站下载解压后即可获得Navicat16安装包和破解补丁,如图所示 2、双击“navicat160_premium_cs_x64.exe”程序,即可进入安装界面, 3、点击下一步 4、如图所示勾选“…...

【看表情包学Linux】初识文件描述符 | 虚拟文件系统 (VFS) 初探 | 系统传递标记位 | O_TRUNC | O_APPEND
爆笑教程《看表情包学Linux》👈 猛戳订阅! 💭 写在前面:通过上一章节的讲解,想必大家已对文件系统基本的接口有一个简单的了解,本章我们将继续深入讲解,继续学习系统传递标志位&…...
ssm+vue“魅力”繁峙宣传网站源码和论文
ssmvue“魅力”繁峙宣传网站源码和论文102 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 摘 要 随着科学技术的飞速发展,各行各业都在努力与现代先进技术接轨,通过科技手段提高自身…...
Linux系统编程5(线程概念详解)
线程同进程一样都是OS中非常重要的部分,线程的应用场景非常的广泛,试想我们使用的视频软件,在网络不是很好的情况下,通常会采取下载的方式,现在你很想立即观看,又想下载,于是你点击了下载并且在…...

leetcode645. 错误的集合(java)
错误的集合 题目描述优化空间代码演示 题目描述 难度 - 简单 LC645 - 错误的集合 集合 s 包含从 1 到 n 的整数。不幸的是,因为数据错误,导致集合里面某一个数字复制了成了集合里面的另外一个数字的值,导致集合 丢失了一个数字 并且 有一个数…...

Pytest参数详解 — 基于命令行模式
1、--collect-only 查看在给定的配置下哪些测试用例会被执行 2、-k 使用表达式来指定希望运行的测试用例。如果测试名是唯一的或者多个测试名的前缀或者后缀相同,可以使用表达式来快速定位,例如: 命令行-k参数.png 3、-m 标记࿰…...

【python爬虫】3.爬虫初体验(BeautifulSoup解析)
文章目录 前言BeautifulSoup是什么BeautifulSoup怎么用解析数据提取数据 对象的变化过程总结 前言 上一关,我们学习了HTML基础知识,知道了HTML是一种用来描述网页的语言,又了解了HTML的基本结构。 认识了HTML中的常见标签和常见属性&#x…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

Mysql故障排插与环境优化
前置知识点 最上层是一些客户端和连接服务,包含本 sock 通信和大多数jiyukehuduan/服务端工具实现的TCP/IP通信。主要完成一些简介处理、授权认证、及相关的安全方案等。在该层上引入了线程池的概念,为通过安全认证接入的客户端提供线程。同样在该层上可…...

Qwen系列之Qwen3解读:最强开源模型的细节拆解
文章目录 1.1分钟快览2.模型架构2.1.Dense模型2.2.MoE模型 3.预训练阶段3.1.数据3.2.训练3.3.评估 4.后训练阶段S1: 长链思维冷启动S2: 推理强化学习S3: 思考模式融合S4: 通用强化学习 5.全家桶中的小模型训练评估评估数据集评估细节评估效果弱智评估和民间Arena 分析展望 如果…...

Spring Boot SQL数据库功能详解
Spring Boot自动配置与数据源管理 数据源自动配置机制 当在Spring Boot项目中添加数据库驱动依赖(如org.postgresql:postgresql)后,应用启动时自动配置系统会尝试创建DataSource实现。开发者只需提供基础连接信息: 数据库URL格…...

【Elasticsearch基础】Elasticsearch批量操作(Bulk API)深度解析与实践指南
目录 1 Bulk API概述 1.1 什么是批量操作 1.2 Bulk API的优势 2 Bulk API的工作原理 2.1 请求处理流程 2.2 底层机制 3 Bulk API的使用方法 3.1 基本请求格式 3.2 操作类型示例 3.3 响应格式 4 Bulk API的最佳实践 4.1 批量大小优化 4.2 错误处理策略 4.3 性能调…...