概率论面试题1:玫瑰花
概率论面试题
1. 一个活动,n个女生手里拿着长短不一的玫瑰花,无序的排成一排,一个男生从头走到尾,试图拿更长的玫瑰花,一旦拿了一朵就不能再拿其他的,错过了就不能回头,问最好的策略?
答:首先确定概率模型,真的很难理解啊!下面这三行公式绕的脑壳疼,其实就是获取“拿到最长的玫瑰花”的最终条件被分解成为两个更容易求解的小条件,即:(1)抽到最长的玫瑰花的概率;(2)在确定最长玫瑰花位置的条件下选中该玫瑰花。
P=P(拿到最长的玫瑰花)=P(最长的玫瑰花⋅拿到该玫瑰花)=P(最长的玫瑰花)∗P(拿到该玫瑰花∣最长的玫瑰花)\begin{align} P&=P(拿到最长的玫瑰花)\\ &=P(最长的玫瑰花·拿到该玫瑰花)\\ &=P(最长的玫瑰花)*P(拿到该玫瑰花|最长的玫瑰花) \end{align} P=P(拿到最长的玫瑰花)=P(最长的玫瑰花⋅拿到该玫瑰花)=P(最长的玫瑰花)∗P(拿到该玫瑰花∣最长的玫瑰花)
现在求取这两个小条件概率,第一条(1),即
P(最长的玫瑰花)=1nP(最长的玫瑰花) = \frac{1}{n} P(最长的玫瑰花)=n1
其中,n为玫瑰花的总数。
第二条非常头疼,这里要充分理解这个条件概率的价值,那便是我们已经知道了最长的玫瑰花在什么位置,那么这样的话就可以通过级数来解决这个问题,具体的图像就不画了,可以参考这个up主讲的视频,挺不错的,这里面的“排队”说法太顶了,直接粘贴图片了。





注:图片搬运自上文所提的UP主的视频中,有兴趣的朋友可以自行观看,讲得很不错。
其中S便是用于进行后续判断的一个位置点,我们所需要的便是获取S点之后的大于1~S之间最大值的值,即:
P(拿到该玫瑰花∣最长的玫瑰花)=SS+SS+1+⋯+Sn−1=S∗(1S+1S+1+⋯+1n−1)=S∗∑i=Sn−11i\begin{align} P(拿到该玫瑰花|最长的玫瑰花)&=\frac{S}{S}+\frac{S}{S+1}+\quad\cdots\quad+\frac{S}{n-1}\\ &=S*(\frac{1}{S}+\frac{1}{S+1}+\quad\cdots\quad+\frac{1}{n-1})\\ &=S*\sum\limits_{i=S}^{n-1}\frac{1}{i} \end{align} P(拿到该玫瑰花∣最长的玫瑰花)=SS+S+1S+⋯+n−1S=S∗(S1+S+11+⋯+n−11)=S∗i=S∑n−1i1
这样的话,最后的P就为:
P=Sn∗∑i=Sn−11i=Sn∫Snn−1n1xdx\begin{align} P&=\frac{S}{n}*\sum\limits_{i=S}^{n-1}\frac{1}{i}\\ &=\frac{S}{n}\int_{\frac{S}{n}}^{\frac{n-1}{n}}\frac{1}{x}dx \end{align} P=nS∗i=S∑n−1i1=nS∫nSnn−1x1dx

P=∑i=Sn−11i=1S+1S+1+⋯+1n−1=1n∗(1Sn+1S+1n+⋯+1n−1n)=1n∗∑i=Snn−1n1in=Sn∫Snn−1n1xdx\begin{align} P&=\sum\limits_{i=S}^{n-1}\frac{1}{i}\\ &=\frac{1}{S}+\frac{1}{S+1}+\quad\cdots\quad+\frac{1}{n-1}\\ &=\frac{1}{n}*(\frac{1}{\frac{S}{n}}+\frac{1}{\frac{S+1}{n}}+\quad\cdots\quad+\frac{1}{\frac{n-1}{n}})\\ &=\frac{1}{n}*\sum\limits_{i=\frac{S}{n}}^{\frac{n-1}{n}}\frac{1}{\frac{i}{n}}\\ &=\frac{S}{n}\int_{\frac{S}{n}}^{\frac{n-1}{n}}\frac{1}{x}dx \end{align} P=i=S∑n−1i1=S1+S+11+⋯+n−11=n1∗(nS1+nS+11+⋯+nn−11)=n1∗i=nS∑nn−1ni1=nS∫nSnn−1x1dx
1n便是每一个小条宽度,而高度则分别是1Sn、1S+1n⋯\frac{1}{n}便是每一个小条宽度,而高度则分别是\frac{1}{\frac{S}{n}}、\frac{1}{\frac{S+1}{n}}\quad\cdots n1便是每一个小条宽度,而高度则分别是nS1、nS+11⋯
图示如下:

总结
学无止境,条件概率、黎曼积分、级数这些知识点都快忘干净了,慌张,抓紧补上吧。
相关文章:

概率论面试题1:玫瑰花
概率论面试题 1. 一个活动,n个女生手里拿着长短不一的玫瑰花,无序的排成一排,一个男生从头走到尾,试图拿更长的玫瑰花,一旦拿了一朵就不能再拿其他的,错过了就不能回头,问最好的策略࿱…...
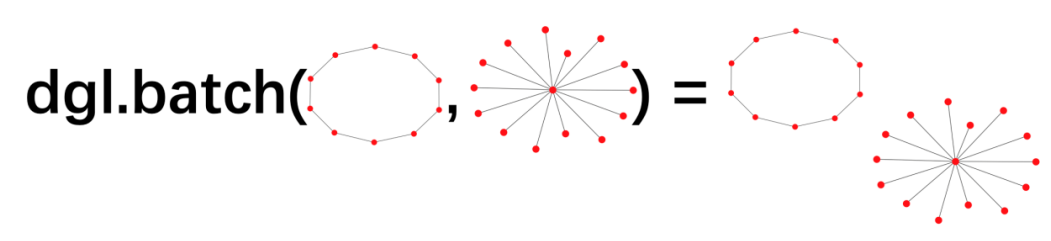
【DGL】图分类
目录概述数据集定义Data LoaderDGL中的batched graph定义模型训练参考概述 除了节点级别的问题——节点分类、边级别的问题——链接预测之外,还有整个图级别的问题——图分类。经过聚合、传递消息得到节点和边的新的表征后,映射得到整个图的表征。 数据…...

时间复杂度的计算(2023-02-10)
时间复杂度的计算 时间复杂度的计算分为三大类:一层循环、二层循环和多层循环。 一层循环 1.找出循环趟数t及每轮循环i的变化值 2.确立循环停止的条件 3.得出t与i之间的关系 4.联立两式,得出结果 eg: void fun(int n) {int i0;while (i*i*i<n)i;…...

测试开发之Django实战示例 第六章 追踪用户行为
第六章 追踪用户行为在之前的章节里完成了小书签将外站图片保存至本站的功能,并且实现了通过jQuery发送AJAX请求,让用户可以对图片进行喜欢/不喜欢操作。这一章将学习如何创建一个用户关注系统和创建用户行为流数据,还将学习Django的信号框架…...

红米9a手动root方法
简介 已知红米6A/6/9/9A/9C/10A机器都可以快速解锁BL,无任何变砖风险 并且秒解锁BL后和官方解锁一样,无任何其他不良影响。推荐大家使用官网解锁,需要等待7天。 BootLoader BootLoader是在操作系统内核运行之前运行的一段小程序。其实…...
)
Open3D 点云最小二乘法拟合平面(剔除噪声,Python版本)
除了诱惑之外,我可以抵抗任何事物。 ----王尔德 文章目录 一、简介二、实现代码三、实现效果参考资料一、简介 这个算法的思路很简单,就是通过剔除一些异常点来拟合更为合适的平面,具体过程如下所示: 1、首先使用最小二乘法拟合一个平面系数的初值。 2、计算所有有效点到拟合…...

【SpringBoot】简述springboot项目启动数据加载内存中的三种方法
一、前言一般来说,SpringBoot工程环境配置放在properties文件中,启动的时候将工程中的properties/yaml文件的配置项加载到内存中。但这种方式改配置项的时候,需要重新编译部署,考虑到这种因素,今天介绍将配置项存到数据…...
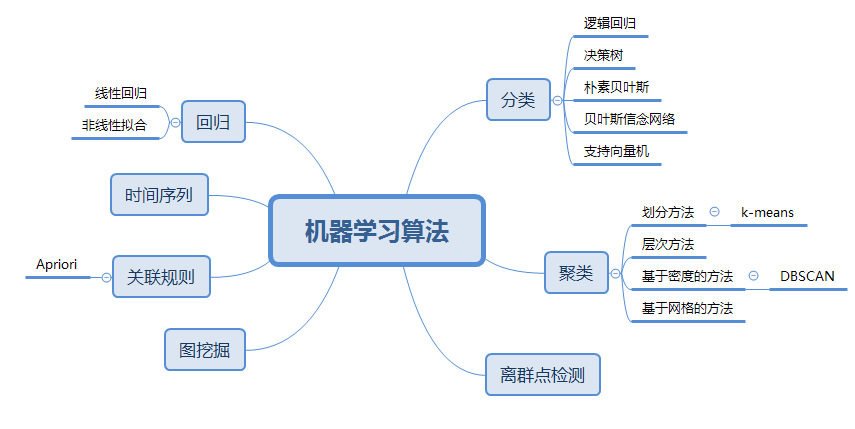
【一文速通】各种机器学习算法的特点及应用场景
近邻 (Nearest Neighbor)KNN算法的核心思想是,如果一个样本在特征空间中的K个最相邻的样本中的大多数属于某一个类别,则该样本也属于这个类别,并具有这个类别上样本的特性。该方法在确定分类决策上只依据最邻近的一个或者几个样本的类别来决定…...

多传感器融合定位十四-基于图优化的定位方法
多传感器融合定位十四-基于图优化的定位方法1. 基于图优化的定位简介1.1 核心思路1.2 定位流程2. 边缘化原理及应用2.1 边缘化原理2.2 从滤波角度理解边缘化3. 基于kitti的实现原理3.1 基于地图定位的滑动窗口模型3.2 边缘化过程4. lio-mapping 介绍4.1 核心思想4.2 具体流程4.…...

PHP基于TCPDF第三方类生成PDF文件
最近在研发招聘的系统 遇到了这个问题 转换pdf 折腾了很久 分享一下PHP基于TCPDF第三方类生成PDF文件最近遇到一个需求,需要根据数据库的字段生成表格式的PDF文件并发送邮箱第一步、我们先去官网上面去下载tcpdf的类:http://www.tcpdf.org/或者是从githu…...
:Sentinel定义资源的方式)
SpringCloud(19):Sentinel定义资源的方式
Sentinel除了基本的定义资源的方式之外,还有其他的定义资源的方式,具体如下: 抛出异常的方式定义资源返回布尔值方式定义资源异步调用支持注解方式定义资源主流框架的默认适配1 抛出异常的方式定义资源 Sentinel中的SphU包含了try-catch风格的API。用这种方式,当资源发生了…...

前端 ES6 之 Promise 实践应用与控制反转
Promise 主要是为解决程序异步处理而生的,在现在的前端应用中无处不在,已然成为前端开发中最重要的技能点之一。它不仅解决了以前回调函数地狱嵌套的痛点,更重要的是它提供了更完整、更强大的异步解决方案。 同时 Promise 也是前端面试中必不…...

LightGBM
目录 1.LightGBM的直方图算法(Histogram) 直方图做差加速 2.LightGBM得两大先进技术(GOSS&EFB) 2.1 单边梯度抽样算法(GOSS) 2.2 互斥特征捆绑算法(EFB) 3.LightGBM得生长策略(leaf-wise) 通过与xgboost对比,在这里列出lgb新提出的几个方面的技术 1.Ligh…...
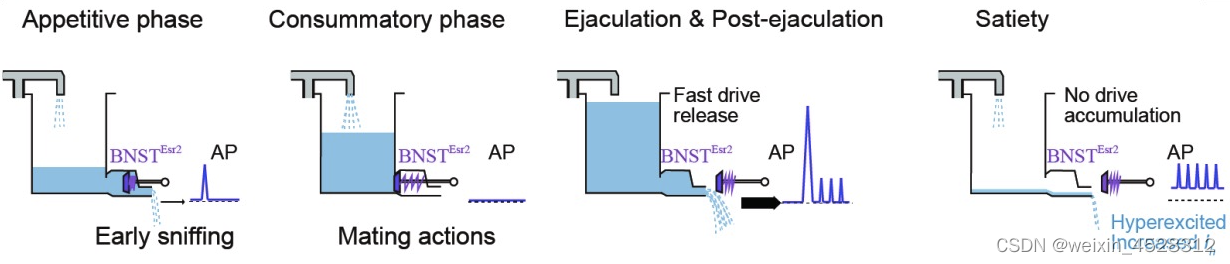
Science:北京脑研究中心李莹实验室揭示性满足感的分子机制
短暂的社交经历(例如,性经历)可导致内部状态的长期变化并影响社会行为,如交配、攻击。例如,在成功交配射精后,许多物种迅速表现出对交配倾向的抑制有数小时、数天或更长时间,这种效应称为性满足…...

Element UI框架学习篇(三)
Element UI框架学习篇(三) 实现简单登录功能(不含记住密码) 1 准备工作 1.1 在zlz包下创建dto包,并创建userDTO类(传输对象) package com.zlz.dto;import lombok.Data;/* DTO 数据传输对象 用户表的传输对象 调用控制器传参使用 VO 控制器返回的视图对象 与页面对应 PO 数据…...
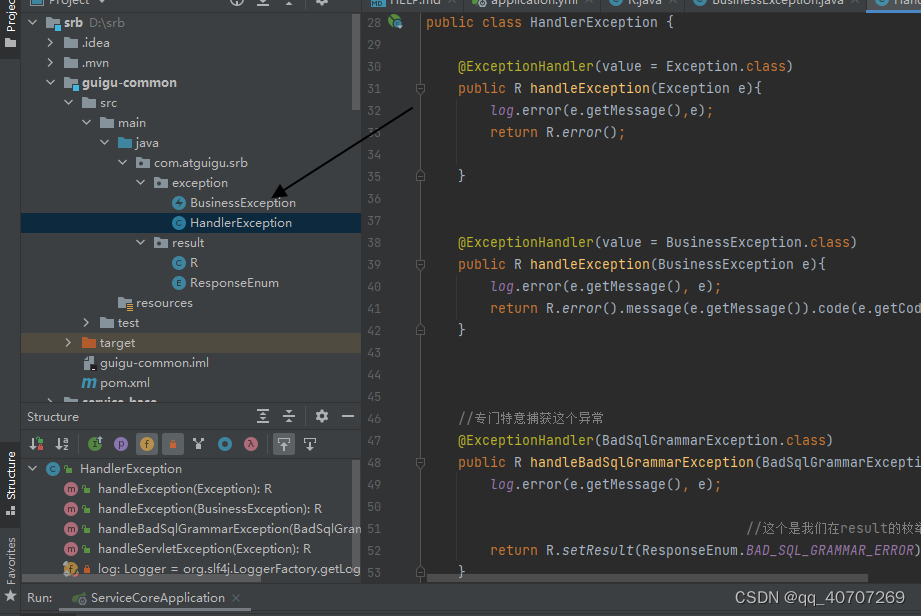
尚硅谷的尚融宝项目
先建立一个Maven springboot项目 进来先把src删掉,因为是一个父项目,我们删掉src之后,pom里配置的东西,也能给别的模块使用。 改一下springboot的版本号码 加入依赖和依赖管理: <properties><java.versi…...

12 Day:内存管理
前言:今天我们要完成我们操作系统的内存管理,以及一些数据结构和小组件的实现,在此之前大家需要了解我们前几天一些重要文件的内存地址存放在哪,以便我们更好的去编写内存管理模块 一,实现ASSERT断言 不知道大家有没有…...

linux基本功系列之lsof命令实战
文章目录前言一. lsof命令介绍二. 语法格式及常用选项三. 参考案例3.1 显示系统打开的文件3.2 查找某个文件相关的进程3.3 列出某个用户打开的文件信息3.4 列出某个程序进程所打开的文件信息3.5 查看某个进程号打开的文件3.6 列出所有的网络连接3.7 列出谁在使用某个端口3.8 恢…...
基础篇:02-SpringCloud概述
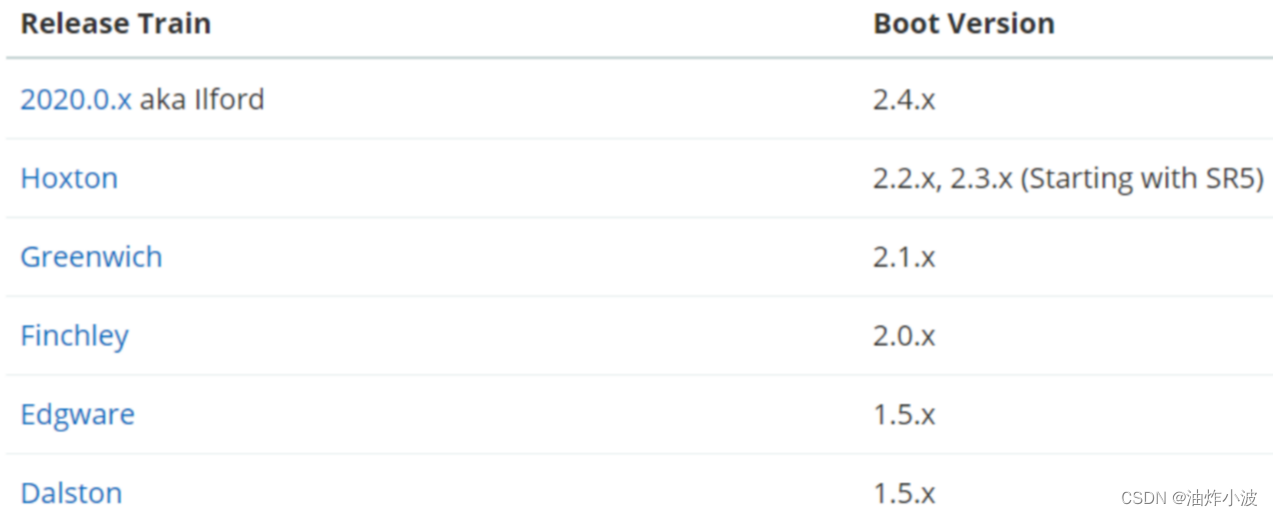
1.SpringCloud诞生 基于前面章节,我们深知微服务已成为当前开发的主流技术栈,但是如dubbo、zookeeper、nacos、rocketmq、rabbitmq、springboot、redis、es这般众多技术都只解决了一个或一类问题,微服务并没有一个统一的解决方案。开发人员或…...
【软件测试】软件测试工作上95%会遇到的问题,你遇到多少?
目录:导读前言一、Python编程入门到精通二、接口自动化项目实战三、Web自动化项目实战四、App自动化项目实战五、一线大厂简历六、测试开发DevOps体系七、常用自动化测试工具八、JMeter性能测试九、总结(尾部小惊喜)前言 1、测试负责人要进行…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
