如何让你的jupyter notebook 排版得像Word(Markdown和网页文件写法)
案例背景
很多时候我们在jupyter notebook里面的写代码,画图,但是文字分析什么的写在里面纯文本不好看,需要进行排版,那么就得用markdown的写法,如何还想居中或者更花里胡哨的字体,那就得要网页文件的一些写法。下面是简单的几个案例,看看怎么排版会好看。
首先介绍一下内嵌span的样式写法参数
| '''1. 字体样式 2. 文本装饰 3. 背景 4. 间距和边框
|
使用演示
<div style="text-align: center;"><span style="color: #661199; font-size: 30px; font-weight: bold; font-family: Arial; text-decoration: underline; background-color: pink; margin: 50px; border: 2px solid black;">这是一段具有多种样式的文本。</span>
</div>
效果不错。颜色,大小,背景什么的都可以按照上面的参数进行修改。
Markdown最主要的功能就是#,有几个#表示几级标题,然后他还有很多项目符号,加粗,阴影,表格等等格式都在下面了,大家可以组合使用,其功能我都写在文字里了。
<div style="text-align: center;"><span style="color: #661199; font-size: 30px; font-weight: bold; font-family: Arial; text-decoration: underline; background-color: pink; margin: 50px; border: 2px solid black;">这是一段具有多种样式的文本。</span>
</div>## <center>网页文件的方法居中显示 </center>
### 三级标题
- **加粗小标题**
- *斜体*+ **<span style='font-size: 20px;'> 改一下字体大看看小 </span>**: 前面*表示加粗了的- **项目符号**: 阴影显示; `阴影显示文本`- 更低级的项目符号, **加粗*** 依靠缩进+ <span style='color:#777777; font-size: 14px;background-color:pink;'> 这里面变颜色 </span>- 缩进进进+ -+*都可以- **文本例子**:```>>> '要用反引号括起来'>>> 哈哈```
>引用文本,下面那个是分割线
---
1. 有序列表1
2. 有序列表2
4. 列表4(显示3)
10. [插入链接]
[https://www.baidu.com]| 列1 | 列2 |
| ------- | ------- |
| 单元格1 | 单元格2 |
[在下面直接写格子]
这样也行?|奇奇怪怪
好像不需要--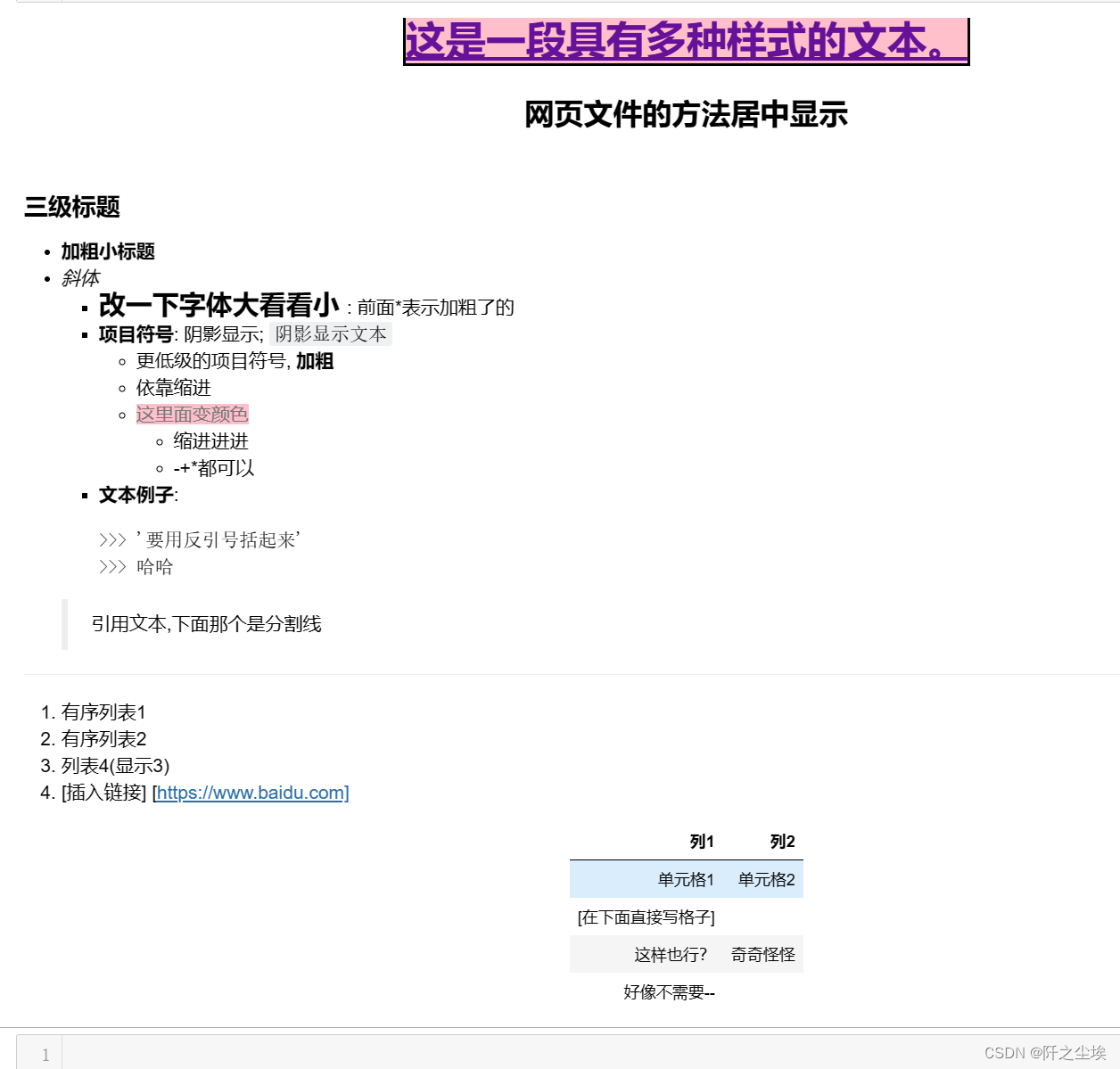
相关文章:

如何让你的jupyter notebook 排版得像Word(Markdown和网页文件写法)
案例背景 很多时候我们在jupyter notebook里面的写代码,画图,但是文字分析什么的写在里面纯文本不好看,需要进行排版,那么就得用markdown的写法,如何还想居中或者更花里胡哨的字体,那就得要网页文件的一些…...
AndroidTV端:酒店扫码认证投屏DLNA
被老板叼了几次了,最近实在忍不了,准备离职; 但是担心离职后长时间没有办法找到工作 就想贡献一套平时琢磨出来的程序,请各位有能力的话带我熬过这凛冽的寒冬。 目前写出来的,有三个端:安卓TV端…...
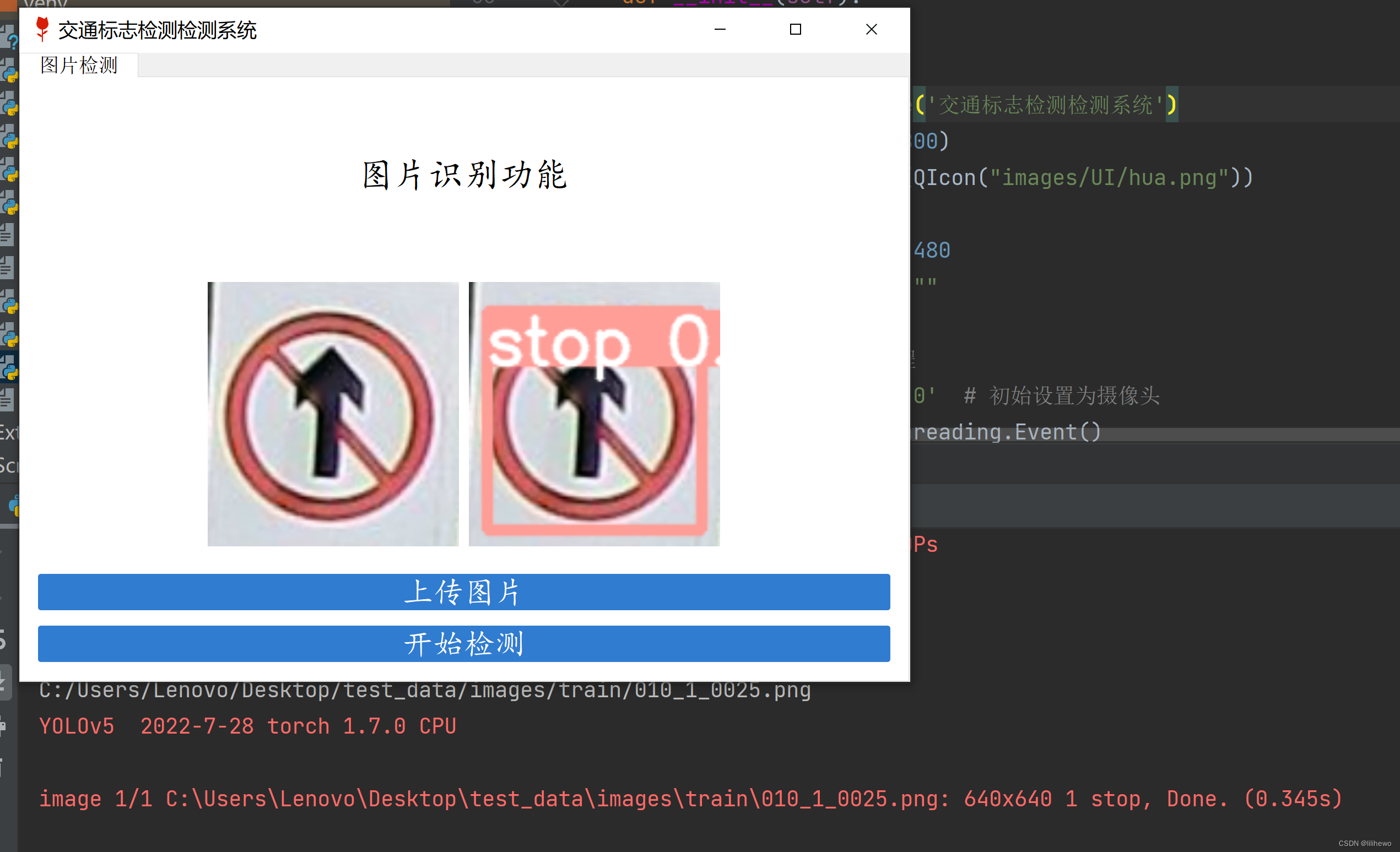
基于PyTorch的交通标志目标检测系统
一、开发环境 Windows 10PyCharm 2021.3.2Python 3.7PyTorch 1.7.0 二、制作交通标志数据集,如下图 三、配置好数据集的地址,然后开始训练 python train.py --data traffic_data.yaml --cfg traffic_yolov5s.yaml --weights pretrained/yolov5s.pt --e…...

feign调用失败 feign.RetryableException: xxx-service executing GET http://xxx/test
一。 问题引入 升级springcloud的版本后 突然发现 以前正常的feign调用也报错了 升级后的各组件版本如下 spring cloud 2021.0.5 spring cloud alibaba 2021.0.5.0 spring boot 2.6.13 错误日志如下 feign.RetryableException: xxx-service executing GET http://xxx-servic…...

mysql 用户管理
目录 用户 创建用户 删除用户 修改密码 权限管理 赋权 查看权限 插销权限 总结 用户 mysql 的用户都存在于系统数据库 mysql 的user 表中 mysql> show tables; --------------------------- | Tables_in_mysql | --------------------------- | column…...

pyinstaller打包exe运行闪退
这里写自定义目录标题 前言问题描述解决过程 前言 闪退原因可能有很多,这里记录下我遇到的问题,简单来说是dll调用错误导致的闪退,因为我的python用的是32位的,但是pyinstaller却是64位的,属于用conda的时候没注意。 …...
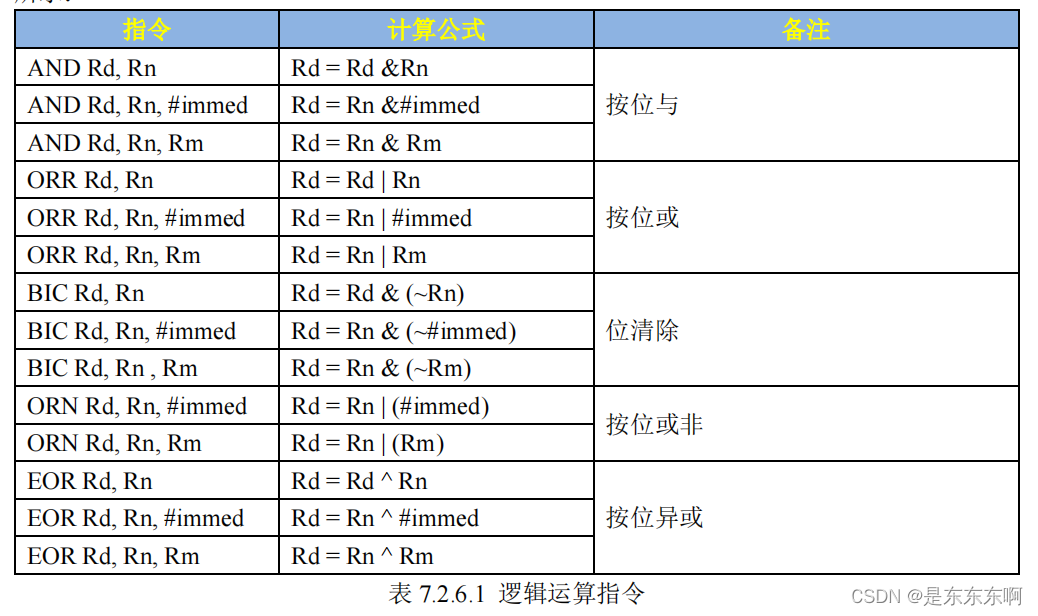
ARM 汇编基础知识
1.为什么学习汇编? 我们在进行嵌入式 Linux 开发的时候是绝对要掌握基本的 ARM 汇编,因为 Cortex-A 芯片一 上电 SP 指针还没初始化, C 环境还没准备好,所以肯定不能运行 C 代码,必须先用汇编语言设置好 C 环境…...

CRM 自动化如何改善销售和客户服务?
许多 B2B 和 B2C 公司都使用 CRM 系统来组织业务流程,使复杂的任务更容易完成。企业可以使用 CRM 自动化来自动化工作流程,让团队有更多的时间来执行高价值的任务,而不是陷于一堆琐碎事情中。 什么是CRM自动化? CRM 自动化是指 C…...

Bean 的六种作用域
目录 一、作用域是什么? 1、singleton(单例作用域) 2、prototype(原型作用域) 3、request(请求作用域) 4、session(回话作用域) 5、application(全局作用域&a…...
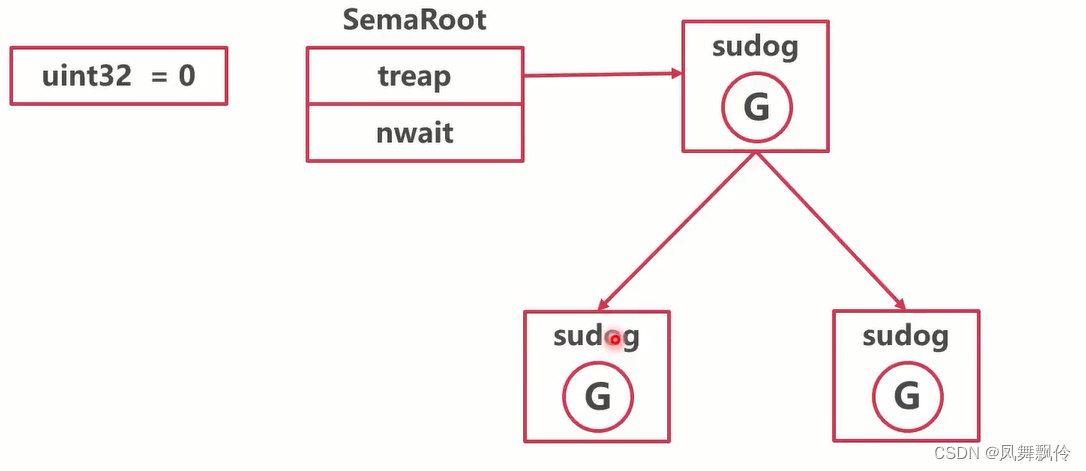
go语言--锁
锁的基础,go的锁是构建在原子操作和信号锁之上的 原子锁 原子包实现协程的对同一个数据的操作,可以实现原子操作,只能用于简单变量的简单操作,可以把多个操作变成一个操作 sema锁 也叫信号量锁/信号锁 核心是一个uint32值&#…...

再见,CSDN
从我2018年1月31日加入CSDN,到现在已经5年多的时间了。在这5年里,陆陆续续在CSDN上发布了很多论文阅读笔记、教程、技术文章等等,记录了我从大四到研究生再到工作这段时间的学习和成长轨迹。 我一直有备份个人资料的习惯,尤其是耗…...
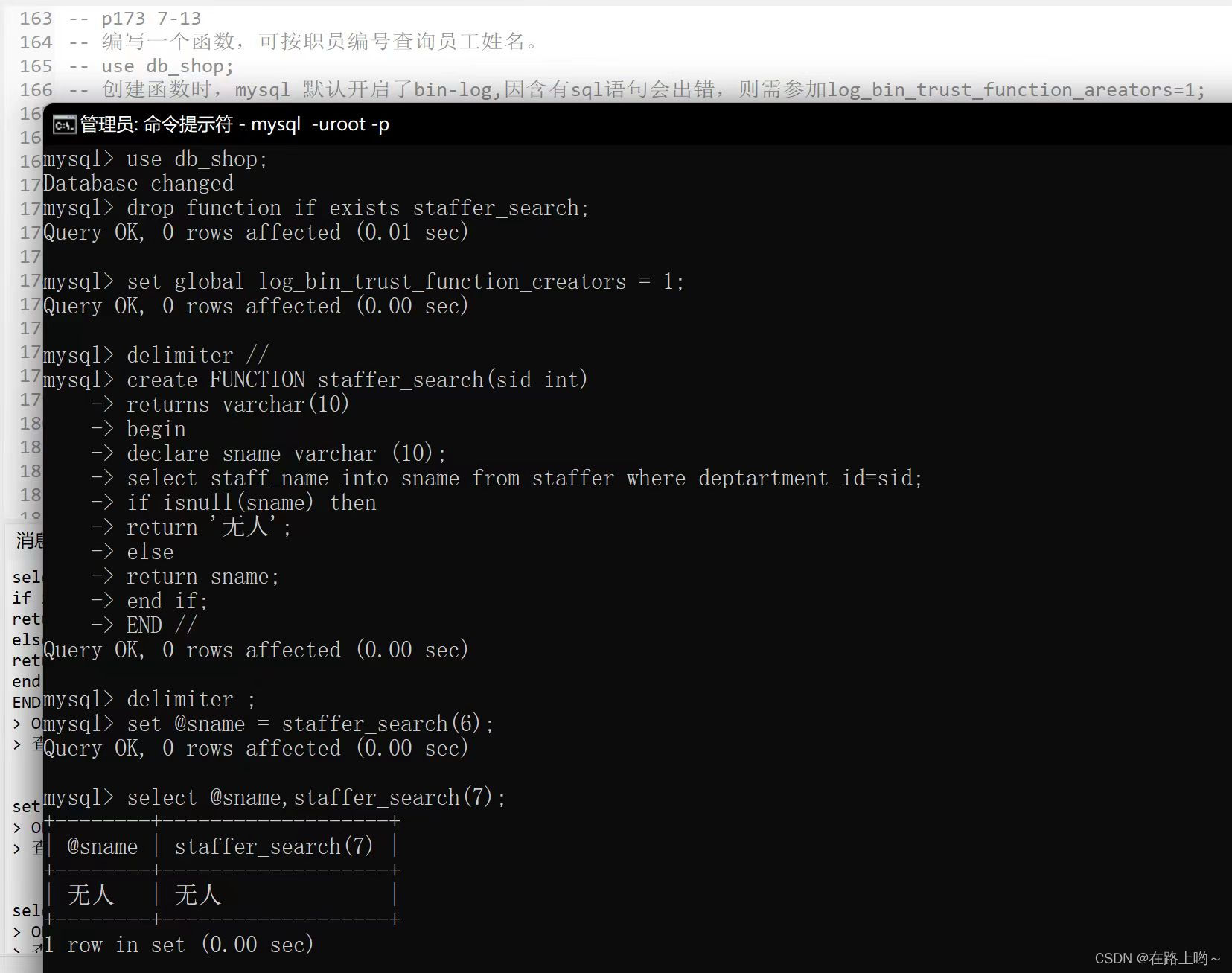
MySQL总复习
目录 登录 显示数据库 创建数据库 删除数据库 使用数据库 创建表 添加数据表数据 查询表 添加数据表多条数据 查询表中某数据 增insert 删delete 改update 查select where like 编辑 范围查找 order by 聚合函数 count max min sum avg g…...
桌面平台层安全随手记录
声明 本文是学习桌面云安全技术要求. 而整理的学习笔记,分享出来希望更多人受益,如果存在侵权请及时联系我们 桌面平台层安全 桌面接入安全 用户标识 一般要求 本项要求包括: a) 系统应为用户提供唯一的身份标识,同时将用户的身份标识与该用户的所…...
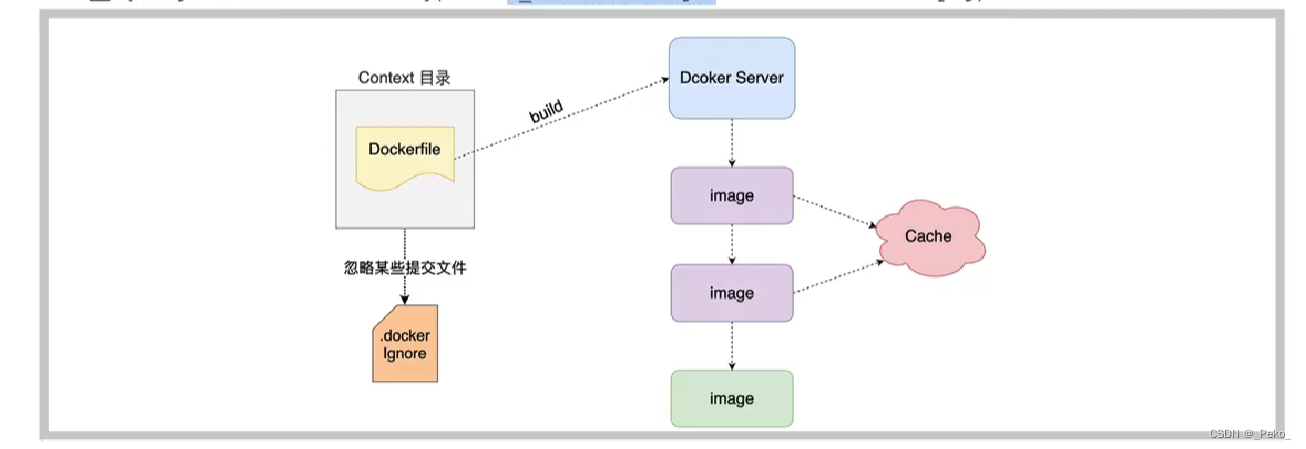
【Docker】 08-Dockerfile
什么是Dockerfile Dockerfile可以认为是Docker镜像的描述文件,是由一系列命令和参数构成的教程,主要作用是用来构建docker镜像的构建文件。 Dockerfile解析过程 Dockerfile的保留命令 保留字作用FROM当前镜像是基于哪个镜像的 第一个指令必须是FROMMA…...
【二等奖方案】大规模金融图数据中异常风险行为模式挖掘赛题「Aries」解题思路
第十届CCF大数据与计算智能大赛(2022 CCF BDCI)已圆满结束,大赛官方竞赛平台DataFountain(简称DF平台)正在陆续释出各赛题获奖队伍的方案思路,欢迎广大数据科学家交流讨论。 本方案为【大规模金融图数据中…...
Github 下载指定文件夹(git sparse-checkout)
比如要下载这里的 data_utils 步骤 1、新建空文件夹,并进入新建的空文件夹。 2、git init 初始化 3、git remote add origin 添加远程仓库 4、git config core.sparsecheckout true 允许稀疏检出 5、git sparse-checkout set 设置需要拉取的文件夹(可…...

蚂蚁集团SQLess 开源,与内部版有何区别?
当我们使用关系型数据库时,SQL 是联系起用户和数据库的一座桥梁。 SQL 是一种高度非过程化的语言,当我们在编写SQL 时,表达的是想要什么数据,而不是怎么获取数据。因此,我们往往更关心SQL 有没有满足业务逻辑ÿ…...

An Efficient Memory-Augmented Transformer for Knowledge-Intensive NLP Tasks
本文是LLM系列文章,针对《An Efficient Memory-Augmented Transformer for Knowledge 一种用于知识密集型NLP任务的高效内存增强转换器 摘要1 引言2 相关工作3 高效内存增强Transformer4 EMAT的训练流程5 实验6 分析7 结论局限性 摘要 获取外部知识对于许多自然语言…...

Java项目中jar war pom包的区别
1、pom:用在父级工程或聚合工程中,用来做jar包的版本控制,必须指明这个聚合工程的打包方式为pom。 <project ...> <modelVersion>4.0.0</modelVersion> <groupId>com.wong.tech</groupId> <artifactI…...

整理mongodb文档:分页
个人博客 整理mongodb文档:分页 个人博客,求关注,如果文章不够清晰,麻烦指出。 文章概叙 本文主要讲下在聚合以及crud的find方法中如何使用limit还有skip进行排序。 分页的情况很经常出现,这也是这篇博客诞生的理由。 数据准备…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...
)
GitHub 趋势日报 (2025年06月06日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 590 cognee 551 onlook 399 project-based-learning 348 build-your-own-x 320 ne…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...
