【二等奖方案】大规模金融图数据中异常风险行为模式挖掘赛题「Aries」解题思路
第十届CCF大数据与计算智能大赛(2022 CCF BDCI)已圆满结束,大赛官方竞赛平台DataFountain(简称DF平台)正在陆续释出各赛题获奖队伍的方案思路,欢迎广大数据科学家交流讨论。
本方案为【大规模金融图数据中异常风险行为模式挖掘】赛题的二等奖获奖方案,赛题地址:https://www.datafountain.cn/competitions/586

获奖团队简介
团队名称:Aries
团队成员:本团队属校企联合团队,由江苏电信和北京师范大学组成,主要研究方向包括数据挖掘,云原生,AI,应用统计分析等,团队具有一定的项目经历和比赛经验。
所获奖项:二等奖
摘 要
随着图数据的日益普及,图挖掘已成为图分析的一项基本任务,其中频繁子图及模式挖掘作为重要一环已经被广泛应用在各个领域。在这个方向已经有大量的文献被发表,并取得了巨大的进步。随着频繁模式挖掘的深入研究,图模型被广泛地应用于为各种事务建模,因此图挖掘的研究显得越来越重要。
针对本赛题要求,本文主要做了以下四个方面工作:1、挖掘出满足阈值要求的的频繁模式。2、精确计算模式频繁的频繁度。3、面向数据编程,尽可能优化程序处理时间。4、使用OpenMP多线程框架,使程序在各个阶段的性能都得到优化。根据本队伍实际执行结果证明上述处理过程可以快速解决问题。
关 键 词
频繁子图,模式挖掘,频繁度
1 背景介绍
1.1 频繁子图挖掘介绍
频繁子图挖掘是数据挖掘中一个非常广泛的应用。频繁子图挖掘是指从大量的图中挖掘出满足给定支持度的频繁子图,同时算法需要保证这些频繁图不能重复。频繁模式挖掘主要就是应用两种策略——Apriori和Growth。最早的AGM和FSG就分别实现了这两重策略的基本思想。gSpan是一个非常高效的算法,它利用dfs-code序列对搜索树进行编码,并且制定一系列比较规则,从而保证最后只得到序列“最小”的频繁图集合。在频繁模式挖掘算法中,常用方法是先计算候选模式的可能性空间,再确定频繁度,由于查找子图模式需要判断子图同构,而判断子图同构是NP完全问题[1],因此计算代价非常大。基于单一大图频繁子图挖掘、频繁图模式挖掘算法GRAMI[2]可以利用多种巧妙的剪枝算法提升挖掘性能。子图生成过程中采用了GSAPN中的最右路扩展,从而保证了搜索空间是完备的。在计算图的支持度时,理论上也是精确的。但算法也提供了支持度的近似算法,近似算法保证了挖掘的子图一定是频繁的,但不是所有频繁的子图都能获得,如果要获得所有频繁子图需要调整支持度大小。
1.2 本题方案简介
本赛题使用简化的金融仿真数据,数据带有时间戳和金额的账户间交易、转账等数据。基于此数据自动挖掘出不小于频繁度(f >= 10000)的频繁子图模式集合。判定子图同构的方法需要属性值匹配,包括交易金额、策略名、业务编码及名称。子图只需匹配到3阶(3条边)子图,频繁度指标需满足单调性要求。
本方案主要将频繁子图挖掘分为两个个阶段:1:剪枝阶段。按题目模式匹配的要求计算出每条边的频繁度,根据单调性要求,将不满足支持度的边去掉,可以为后面挖掘二阶三阶子图省去大量无效遍历。2:精确计算频繁度阶段。利用近似的频繁模式,根据单调性要求,精确计算出满足阈值要求的模式频繁度。具体流程图见图1.

图1
2 算法设计与实现
我们将整体流程细分为5个步骤,分别是输入、构图、剪枝、频繁度计算和输出。首先,需要将数据文检读取进内存,用方便读取的数据结构存储,因为是有向图需要用偏移范围作索引,可以实现根据边起点的随机遍历。之后利用边数据属性值将边编码成一个整数,用整型数组对模式计数,删除不满足支持度要求的边,因为基于单调性,其拓展的图也不频繁。这样可以大大缩小了边的数据规模。对候选模式求频繁度,由于候选模式较少,可以用二维数组遍历一次即可求出所有模式的频繁度。在输入、构图、剪枝和频繁度四个阶段都是用OpenMP并行处理,大大提高了程序运行效率。
2.1 输入和构图
输入部分主要是从点数据文件和边数据文件读入数据,数据约748MB,因为数据量较大,读数据需要花很多时间,因此需要提高文件读取速度,我们团队采用mmap系统调用的方法读取文件,将数据存储到数组中。由于本赛题不仅考察答案的准确率,相同答案的情况下程序的运行时间也作为考察依据,为了加速文件读取速度,我们采用多线程读取,使用mmap映射后,根据文件的首地址和文件长度,按照字节长度将文件分配到多个任务中。上述为点数据的读取。
struct Edge {
uint32_t to;
uint32_t amt;
uint32_t strategy;
uint32_t buscode;
} *edges;
uint32_t *loc;
边数据读取较为特殊,为了能方便后续算法根据起点可以快速遍历,首先用多线程遍历一次边文件,将每个线程计算出的起点边数和汇总在一个数组loc中,这样若搜索定点s的边的时候,其边的范围就是[loc[s],loc[s+1]]。结构体中只存边的属性和目标点的信息。
2.2 剪枝
读取的原始数据中,很多边是不能满足频繁度要求的,根据单调性的约束,这些边的拓展边也不会满足单调性约束,所以需要将这些无效边删除,这样可以加速后续的处理。本方案使用flag数组标记边的有效性,遍历时遇到无效边,就直接跳过。为了高效计数,我们没有使用dfs-code编码,而是根据边的属性映射到整数上,通过一个整型数组作为计数器。例如一条边的属性为{from:1,to:1,aim:0,strategy:1,buscode:1},由于顶点只有3种类型(account_to_card可以用strategy区分),amt通过剪枝后有10种,strategy有6种,buscode有4种,这条边可以描述为1*3*10*6*4+1*10*6*4+0*6*4+6*4+4,所有边都可以通过此方法映射到对应的整数上。这里有个提升性能的方法,在不影响正确结果的情况下,可以适当将调整阈值调大,不过这样会导致和GRAMI[2]算法同样的问题,如果将阈值调整过大,只能保证挖掘的子图一定是频繁的,但不是所有频繁的子图都能获得,所以要根据图调整。
2.3 三阶边频繁度计算
三阶频繁度计算就是根据单调性的约束和阈值约束,求出满足条件的模式的频繁度。通过上述对一阶边的剪枝,可以将剩下的边继续拓展到二阶三阶中,也利用单调性和阈值的约束计算,但由于在处理三阶边的时候数值过大,无法将编码映射到整数中,所以在剪枝后要将边的值重新映射到数组中。重新映射后三阶边也可以映射到数据中,映射方式和一条边类似。这样就可以求出满足条件模式的频繁度。
2.4 输出
将计算出的结果使用fastjosn输出到文件中,输出时间占比较少,所以没用多线程处理。
3 实验结果
程序测试的物理机配置为4核 3.4Ghz服务器,操作系统为ubuntu20.04。我们对程序的各个阶段4个线程和单线程进行了比较,结果如下图2,多线程在各个阶段都显著提高运行速度,整个程序在4个线程下只需要执行0.92s,当然这是本地测试环境的结果,由于硬件配置不同,与线上结果有一些差别。
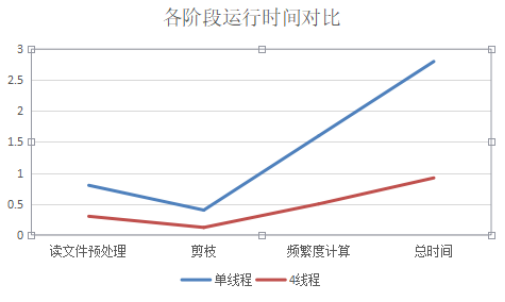
图2
致谢
感谢赛事的所有工作人员,他们默默无闻的努力,无微不至的付出,是支撑大赛顺利运行的坚定基石。感谢队友的努力付出,才能让我们团队进入最终决赛。
参考
[1] Wernicke S. Rasche F. FANMOD: A tool for fast network motif detection. Bioinformatics. 2006. 22(9) : 1152-1153
[2] GraMi:frequent subgraph and pattern mining in a single large graph [J] . Elseidy Mohammed,Abdelhamid Ehab,Skiadopoulos Spiros,Kalnis Panos. Proceedings of the VLDB Endowment . 2014 (7)
我是行业领先的大数据竞赛平台 @DataFountain ,欢迎广大政企校军单位合作办赛,推动优秀数据人才揭榜挂帅!
相关文章:

【二等奖方案】大规模金融图数据中异常风险行为模式挖掘赛题「Aries」解题思路
第十届CCF大数据与计算智能大赛(2022 CCF BDCI)已圆满结束,大赛官方竞赛平台DataFountain(简称DF平台)正在陆续释出各赛题获奖队伍的方案思路,欢迎广大数据科学家交流讨论。 本方案为【大规模金融图数据中…...
Github 下载指定文件夹(git sparse-checkout)
比如要下载这里的 data_utils 步骤 1、新建空文件夹,并进入新建的空文件夹。 2、git init 初始化 3、git remote add origin 添加远程仓库 4、git config core.sparsecheckout true 允许稀疏检出 5、git sparse-checkout set 设置需要拉取的文件夹(可…...

蚂蚁集团SQLess 开源,与内部版有何区别?
当我们使用关系型数据库时,SQL 是联系起用户和数据库的一座桥梁。 SQL 是一种高度非过程化的语言,当我们在编写SQL 时,表达的是想要什么数据,而不是怎么获取数据。因此,我们往往更关心SQL 有没有满足业务逻辑ÿ…...

An Efficient Memory-Augmented Transformer for Knowledge-Intensive NLP Tasks
本文是LLM系列文章,针对《An Efficient Memory-Augmented Transformer for Knowledge 一种用于知识密集型NLP任务的高效内存增强转换器 摘要1 引言2 相关工作3 高效内存增强Transformer4 EMAT的训练流程5 实验6 分析7 结论局限性 摘要 获取外部知识对于许多自然语言…...

Java项目中jar war pom包的区别
1、pom:用在父级工程或聚合工程中,用来做jar包的版本控制,必须指明这个聚合工程的打包方式为pom。 <project ...> <modelVersion>4.0.0</modelVersion> <groupId>com.wong.tech</groupId> <artifactI…...

整理mongodb文档:分页
个人博客 整理mongodb文档:分页 个人博客,求关注,如果文章不够清晰,麻烦指出。 文章概叙 本文主要讲下在聚合以及crud的find方法中如何使用limit还有skip进行排序。 分页的情况很经常出现,这也是这篇博客诞生的理由。 数据准备…...
社区团购新玩法,生鲜蔬菜配货发货小程序商城
在当前的电商市场中,生鲜市场具有巨大的潜力和发展空间。为了满足消费者的需求,许多生鲜店正在寻找创新的方法来提高销售和客户满意度。其中,制作一个个性且功能强大的生鲜小程序商城是一个非常有效的策略。以下是在乔拓云平台上制作生鲜小程…...

shell bash中设置命令set
1 Preface/Foreword set命令用于shell脚本在执行命令时候,遇到异常的处理机制。 2 Usage 2.1 set -e 当执行命令过程中遇到异常,那么就退出脚本,不会往下执行其它命令。 #!/bin/bash #set -eroot GIT_TAG${CI_BUILD_TAG-NOTAG} GIT_REV…...
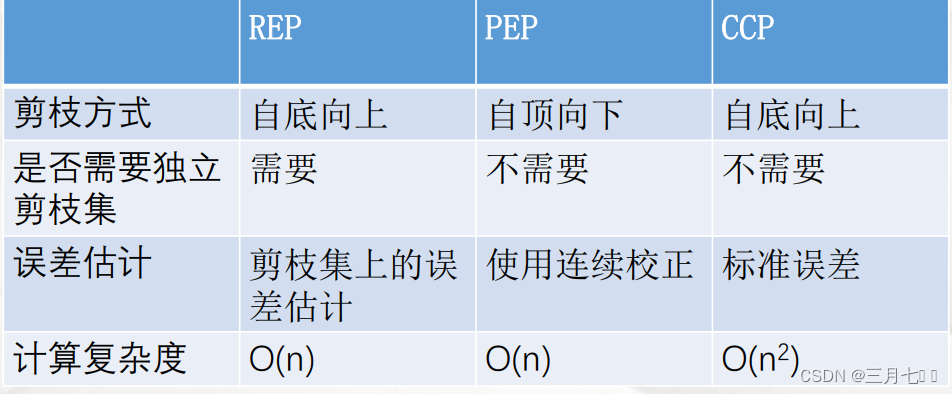
机器学习---预剪枝、后剪枝(REP、CCP、PEP、)
1. 为什么要进行剪枝 横轴表示在决策树创建过程中树的结点总数,纵轴表示决策树的预测精度。 实线显示的是决策树 在训练集上的精度,虚线显示的则是在⼀个独⽴的测试集上测量出来的精度。 随着树的增⻓,在 训练样集上的精度是单调上升的&…...

Python 爬虫—scrapy
scrapy用于从网站中提取所需数据的开源协作框架。以一种快速、简单但可扩展的方式。 该爬虫框架适合于那种静态页面, js 加载的话,如果你无法模拟它的 API 请求,可能就需要使用 selenium 这种使用无头浏览器的方式来完成你的需求了 入门 imp…...
ABB机器人20032转数计数器未更新故障报警处理方法
ABB机器人20032转数计数器未更新故障报警处理方法 ABB的机器人上面安装有电池,需要定期进行更换(正常一年换一次),如果长时间不更换,电量过低,就会出现转数计数器未更新的报警,各轴编码器的位置就会丢失,在更换新电池后,需要更新转数计数器。 具体步骤如下: 先用手动…...

C# 记事本应用程序
using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System...

模型训练:优化人工智能和机器学习,完善DevOps工具的使用
作者:JFrog大中华区总经理董任远 据说法餐的秘诀在于黄油、黄油、更多的黄油。同样,对于DevOps而言,成功的三大秘诀是自动化、自动化、更高程度的自动化,而这一切归根结底都在于构建能够更快速地不断发布新版软件的流程。 尽管人…...
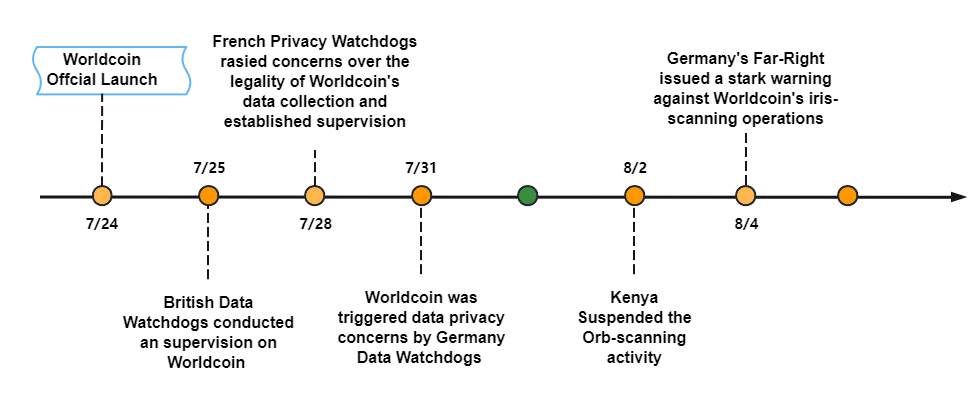
WorldCoin 运营数据,业务安全分析
WorldCoin 运营数据,业务安全分析 Worldcoin 的白皮书中声明,Worldcoin 旨在构建一个连接全球人类的新型数字经济系统,由 OpenAI 创始人 Sam Altman 于 2020 年发起。通过区块链技术在 Web3 世界中实现更加公平、开放和包容的经济体系&#…...

Java之Calender类的详细解析
Calendar类 3.1 概述 java.util.Calendar类表示一个“日历类”,可以进行日期运算。它是一个抽象类,不能创建对象,我们可以使用它的子类:java.util.GregorianCalendar类。 有两种方式可以获取GregorianCalendar对象: …...
uniapp 微信小程序 锚点跳转
uniapp文档 以下是我遇到的业务场景,是点击商品分类的某一类 然后页面滚动至目标分类, 首先第一步是设置锚点跳转的目的地,在目标的dom上面添加id属性 然后给每个分类每一项添加点击事件,分类这里的item数据里面有一字段是和上…...

主成分分析笔记
主成分分析是指在尽量减少失真的前提下,将高维数据压缩成低微的方式。 减少失真是指最大化压缩后数据的方差。 记 P P P矩阵为 n m n\times m nm( n n n行 m m m列)的矩阵,表示一共有 m m m组数据,每组数据有 n n n…...
android studio 的 adb配置
首先在 Android Studio 中 打开 File -> Settings: 下载 “Google USB Driver” 这个插件 (真机调试的时候要用到), 并且记一下上面的SDK路径: 右键桌面上的 “我的电脑”, 点击 “高级系统设置”, 配置计算机的高级属性, 有两步: 添加一个新的环境变量 ANDROID_HOME, 变量…...

【HTML5高级第一篇】Web存储 - cookie、localStorage、sessionStorage
文章目录 一、数据存储1.1 cookie1.1.1 概念介绍1.1.2 存储与获取1.1.3 方法的封装1.1.4 总结 1.2 localstorage 与 sessionstorage1.2.1 概述1.2.2 操作数据的属性或方法1.2.3 案例-提交问卷1.2.4 Web Storage带来的好处 附录:1. HTML5提供的数据持久化技术&#x…...
Flink---1、概述、快速上手
1、Flink概述 1.1 Flink是什么 Flink的官网主页地址:https://flink.apache.org/ Flink的核心目标是“数据流上有状态的计算”(Stateful Computations over Data Streams)。 具体说明:Apache Flink是一个“框架和分布式处理引擎”,用于对无界…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

生成xcframework
打包 XCFramework 的方法 XCFramework 是苹果推出的一种多平台二进制分发格式,可以包含多个架构和平台的代码。打包 XCFramework 通常用于分发库或框架。 使用 Xcode 命令行工具打包 通过 xcodebuild 命令可以打包 XCFramework。确保项目已经配置好需要支持的平台…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

什么是Ansible Jinja2
理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具,可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板,允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板,并通…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
