主成分分析笔记
主成分分析是指在尽量减少失真的前提下,将高维数据压缩成低微的方式。
减少失真是指最大化压缩后数据的方差。
记 P P P矩阵为 n × m n\times m n×m( n n n行 m m m列)的矩阵,表示一共有 m m m组数据,每组数据有 n n n个维度。
欲将此数据集降为 k k k维,即求 k × m k\times m k×m的矩阵 A A A。
思路是获得一种针对 n n n维的变换方法,将 n n n位列向量转为 k k k位列向量。然后对全部 m m m组数据分别应用此变换,这样就得到答案。
变换方法是使用形如 A = X P A=XP A=XP的算式。问题变为求 k × n k\times n k×n矩阵 X X X。
引入协方差的概念。
协方差是刻画两个列向量 X = { x 1 , x 2 , … , x n } T , Y = { y 1 , y 2 , … , y n } T X=\{x_1,x_2,\dots,x_n\}^\text{T},Y=\{y_1,y_2,\dots,y_n\}^\text{T} X={x1,x2,…,xn}T,Y={y1,y2,…,yn}T的相异程度。对于同一行来说,两个列向量在此行的数值相差越大,就会使协方差越大。
C o v ( X , Y ) = ∑ i = 1 n ( x i − x ^ ) ( y i − y ^ ) Cov(X,Y)=\sum_{i=1}^{n}{(x_i-\hat{x})(y_i-\hat{y})} Cov(X,Y)=i=1∑n(xi−x^)(yi−y^)
接下来的部分需要线性代数理论进行推导,在此只给出结论。
对于数据集的 n n n个维度来说,方差越大,说明数据之间的差异越大,说明越能区分不同数据,说明此维度越重要,越应该被保留。可以用协方差刻画差异。
本例中将关于 n n n维的所有协方差写成一个 n n n阶方阵 Q Q Q,其中 Q i , j Q_{i,j} Qi,j表示 C o v ( P i , P j ) Cov(P_i,P_j) Cov(Pi,Pj), P i P_i Pi表示 P P P的第 i i i行,也就是所有数据的第 i i i个维度。
至此便直接给出计算方法。
- 计算 Q Q Q;
- 求 Q Q Q的 n n n个特征值及其对应的特征(行)向量,将它们按照特征值从大到小的顺序排列,组成新的方阵 R R R;
- 取 R R R的前 k k k行,即 k × n k\times n k×n的矩阵 X X X;
- A = X P A=XP A=XP。
相关文章:

主成分分析笔记
主成分分析是指在尽量减少失真的前提下,将高维数据压缩成低微的方式。 减少失真是指最大化压缩后数据的方差。 记 P P P矩阵为 n m n\times m nm( n n n行 m m m列)的矩阵,表示一共有 m m m组数据,每组数据有 n n n…...
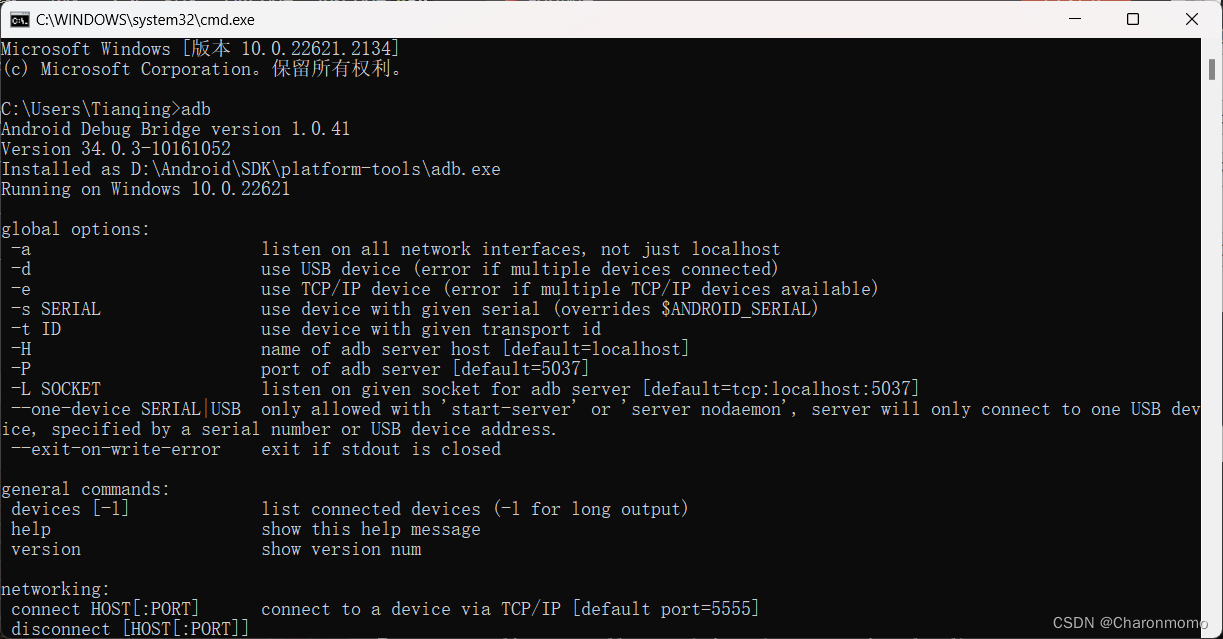
android studio 的 adb配置
首先在 Android Studio 中 打开 File -> Settings: 下载 “Google USB Driver” 这个插件 (真机调试的时候要用到), 并且记一下上面的SDK路径: 右键桌面上的 “我的电脑”, 点击 “高级系统设置”, 配置计算机的高级属性, 有两步: 添加一个新的环境变量 ANDROID_HOME, 变量…...

【HTML5高级第一篇】Web存储 - cookie、localStorage、sessionStorage
文章目录 一、数据存储1.1 cookie1.1.1 概念介绍1.1.2 存储与获取1.1.3 方法的封装1.1.4 总结 1.2 localstorage 与 sessionstorage1.2.1 概述1.2.2 操作数据的属性或方法1.2.3 案例-提交问卷1.2.4 Web Storage带来的好处 附录:1. HTML5提供的数据持久化技术&#x…...
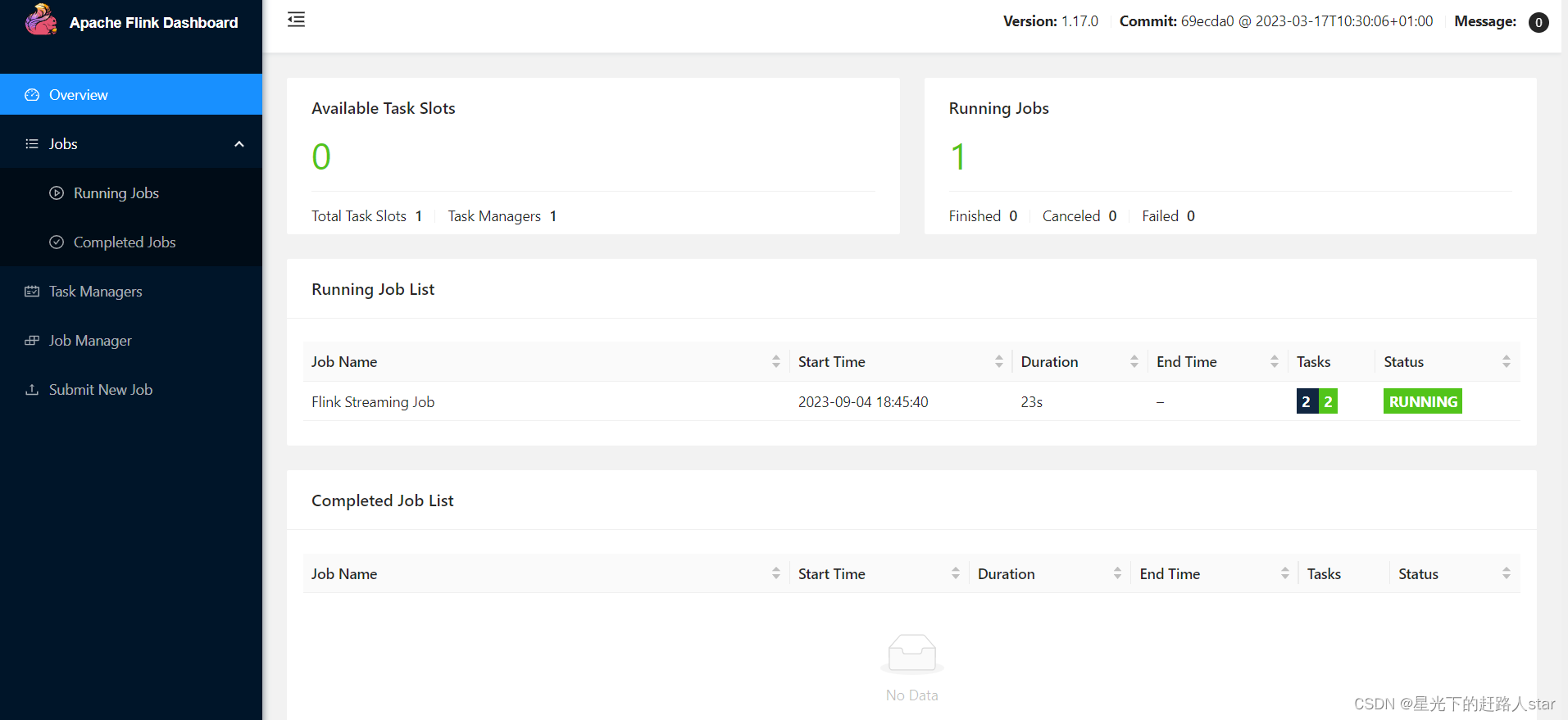
Flink---1、概述、快速上手
1、Flink概述 1.1 Flink是什么 Flink的官网主页地址:https://flink.apache.org/ Flink的核心目标是“数据流上有状态的计算”(Stateful Computations over Data Streams)。 具体说明:Apache Flink是一个“框架和分布式处理引擎”,用于对无界…...
QT实现TCP通信(服务器与客户端搭建)
一、TCP通信框架 二、QT中的服务器操作 创建一个QTcpServer类对象,该类对象就是一个服务器调用listen函数将该对象设置为被动监听状态,监听时,可以监听指定的ip地址,也可以监听所有主机地址,可以通过指定端口号&#x…...

云备份项目
云备份项目 1. 云备份认识 自动将本地计算机上指定文件夹中需要备份的文件上传备份到服务器中。并且能够随时通过浏览器进行查看并且下载,其中下载过程支持断点续传功能,而服务器也会对上传文件进行热点管理,将非热点文件进行压缩存储&…...

基础算法(一)
目录 一.排序 快速排序: 归并排序: 二.二分法 整数二分模板: 浮点二分: 一.排序 快速排序: 从数列中挑出一个元素,称为 "基准"重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面&#…...
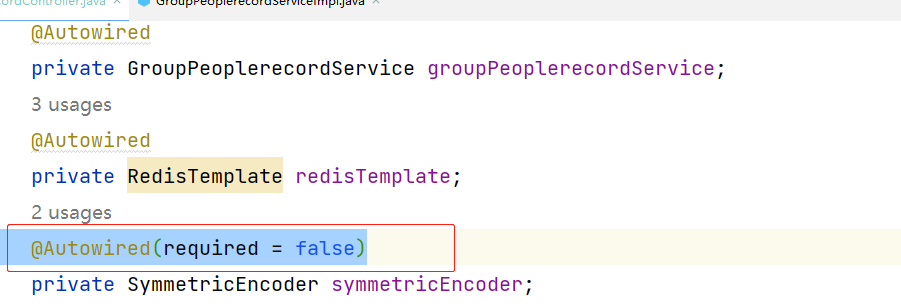
Consider defining a bean of type问题解决
Consider defining a bean of type问题解决 Consider defining a bean of type问题解决 包之后,发现项目直接报错Consider defining a bean of type。 会有一些包你明明Autowired 但是还是找不到什么bean 导致你项目启动不了 解决方法一: 这个问题主要是因为项目拆包…...

Android 1.2.1 使用Eclipse + ADT + SDK开发Android APP
1.2.1 使用Eclipse ADT SDK开发Android APP 1.前言 这里我们有两条路可以选,直接使用封装好的用于开发Android的ADT Bundle,或者自己进行配置 因为谷歌已经放弃了ADT的更新,官网上也取消的下载链接,这里提供谷歌放弃更新前最新…...
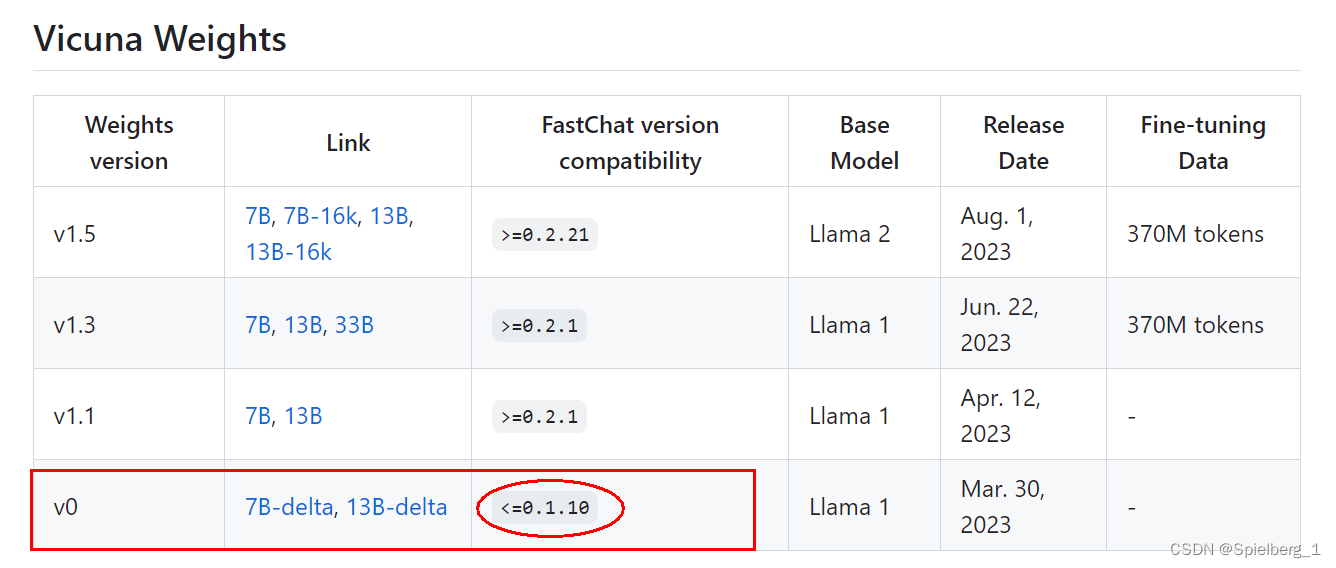
Llama-7b-hf和vicuna-7b-delta-v0合并成vicuna-7b-v0
最近使用pandagpt需要vicuna-7b-v0,重新过了一遍,前段时间部署了vicuna-7b-v3,还是有不少差别的,transforms和fastchat版本更新导致许多地方不匹配,出现很多错误,记录一下。 更多相关内容可见Fastchat实战…...

Centos、OpenEuler系统安装mysql
要在CentOS上安装MySQL并设置开机自启和root密码,请按照以下步骤进行操作: 确保您的CentOS系统已连接到Internet,并且具有管理员权限(root或sudo访问权限)。打开终端或SSH会话,使用以下命令安装MySQL&…...
如何在Win10系统上安装WSL(适用于 Linux 的 Windows 子系统)
诸神缄默不语-个人CSDN博文目录 本文介绍的方法不是唯一的安装方案,但在我的系统上可用。 文章目录 1. 视频版2. 文字版和代码3. 本文撰写过程中使用到的其他网络参考资料 1. 视频版 B站版:在Windows上安装Linux (WSL, 适用于 Linux 的 Windows 子系统…...
单片机通用学习-什么是寄存器?
什么是寄存器? 寄存器是一种特殊的存储器,主要用于存储和检查微机的状态。CPU寄存器用于存储和检查CPU的状态,具体包括计算中途数据、程序因中断或子程序分支时的返回地址、计算结果为零时的负值、计算结果为零时的信息、进位值等。 由于CP…...

【C语言】文件操作详解
文章目录 前言一、文件是什么二、文件具体介绍1.文件名2.文件类型3.文件缓冲区4.文件指针5.文件的打开和关闭 三、文件的顺序读写1.字符输入函数(fgetc)2.字符输出函数(fputc)3.文本行输入函数(fgets)4.文本…...

栈(Stack)的详解
目录 1.栈的概念 2.栈的模拟实现 1.栈的方法 2.模拟栈用(整型)数组的形式呈现 2.1栈的创建 2.2压栈 2.3栈是否为空 2.4出栈 2.5获取栈中有效元素个数 2.6获取栈顶元素 2.7完整代码实现 1.栈的概念 从上图中可以看到, Stack 继承了…...

深入了解GCC编译过程
关于Linux的编译过程,其实只需要使用gcc这个功能,gcc并非一个编译器,是一个驱动程序。其编译过程也很熟悉:预处理–编译–汇编–链接。在接触底层开发甚至操作系统开发时,我们都需要了解这么一个知识点,如何…...

leetcode 594.最长和谐子序列(滑动窗口)
⭐️ 题目描述 🌟 leetcode链接:最长和谐子序列 思路: 第一步先将数组排序,在使用滑动窗口(同向双指针),定义 left right 下标,比如这一组数 {1,3,2,2,5,2,3,7} 排序后 {1,2,2,2,3,…...

深入剖析云计算与云服务器ECS:从基础到实践
云计算已经在不断改变着我们的计算方式和业务模式,而云服务器ECS(Elastic Compute Service)作为云计算的核心组件之一,为我们提供了灵活、可扩展的计算资源。在本篇长文中,我们将从基础开始,深入探讨云计算…...
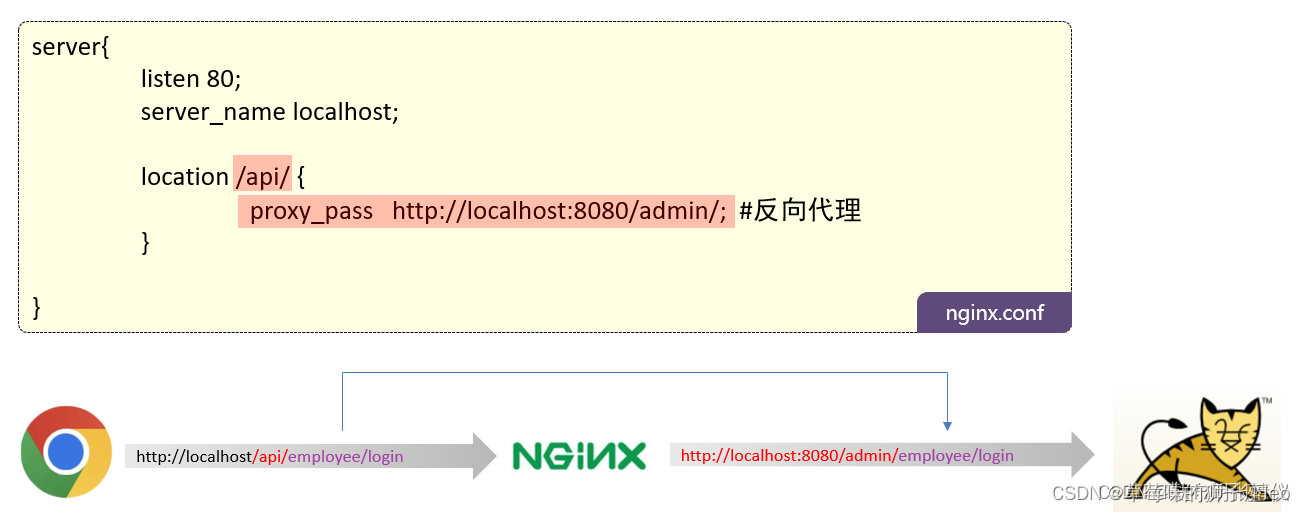
苍穹外卖技术栈
重难点详解 1、定义全局异常 2、ThreadLocal ThreadLocal 并不是一个Thread,而是Thread的一个局部变量ThreadLocal 为每一个线程提供独立的存储空间,具有线程隔离的效果,只有在线程内才能取到值,线程外则不能访问 public void …...

重新开始 杂类:C++基础
目录 1.输入输出 2 . i 与 i 3.结构体 4.二进制 1.输入输出 #include<cstdio>//cin>>,cout #include<iostream>//printf,scanf (1) cin , cout输入输出流可直接用于数字,字符 (2)scanf(&quo…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

R语言速释制剂QBD解决方案之三
本文是《Quality by Design for ANDAs: An Example for Immediate-Release Dosage Forms》第一个处方的R语言解决方案。 第一个处方研究评估原料药粒径分布、MCC/Lactose比例、崩解剂用量对制剂CQAs的影响。 第二处方研究用于理解颗粒外加硬脂酸镁和滑石粉对片剂质量和可生产…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Scrapy-Redis分布式爬虫架构的可扩展性与容错性增强:基于微服务与容器化的解决方案
在大数据时代,海量数据的采集与处理成为企业和研究机构获取信息的关键环节。Scrapy-Redis作为一种经典的分布式爬虫架构,在处理大规模数据抓取任务时展现出强大的能力。然而,随着业务规模的不断扩大和数据抓取需求的日益复杂,传统…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

简单介绍C++中 string与wstring
在C中,string和wstring是两种用于处理不同字符编码的字符串类型,分别基于char和wchar_t字符类型。以下是它们的详细说明和对比: 1. 基础定义 string 类型:std::string 字符类型:char(通常为8位)…...

OpenGL-什么是软OpenGL/软渲染/软光栅?
软OpenGL(Software OpenGL)或者软渲染指完全通过CPU模拟实现的OpenGL渲染方式(包括几何处理、光栅化、着色等),不依赖GPU硬件加速。这种模式通常性能较低,但兼容性极强,常用于不支持硬件加速…...
