当前位置： 首页 > news >正文

第五课：C++实现加密PDF文档解密

news 2026/4/4 9:23:22

请注意，未经授权的加密PDF文件解密是非法的，本文仅为学术和研究目的提供参考。

  1. 打开加密的PDF文件并获取密钥 在C++中，可以使用pdfium库打开加密的PDF文件。使用pdfium库中的FPDF_LoadCustomDocument函数可以打开具有自定义访问权限的加密文件。该函数接受一个IFX_FileRead*类型的参数，用于读取文件内容。通过该函数打开PDF文件后，可以使用FPDF_GetSecurityHandlerCount函数检索安全处理程序的数量。如果安全处理程序的数量为1，则可以使用FPDF_GetSecurityHandlerRevision函数和FPDF_GetSecurityHandlerString函数获取安全处理程序的版本和密钥。

  2. 解密PDF文档 使用获取的密钥，可以使用pdfium库中的FPDF_SetCipherHandler函数将打开的文件解密。该函数接受一个IFX_FileRead*类型的参数，用于读取文件内容。此函数还需要导入PDF的打开方式以及文件的密码。一旦文档被成功解密，FPDF_LoadCustomDocument函数会调用，然后就可以对其进行操作。

  3. 保存解密后的PDF文件 对于解密后的PDF文件，可以使用pdfium库中的FPDF_SaveAsCopy函数将其保存到新的PDF文件中。该函数需要指定要保存的PDF文件的名称，并将已解密的PDF文件作为参数传递。保存成功后，可以使用FPDF_CloseDocument函数关闭解密后的PDF文件。

示例代码：

#include <stdio.h>
#include "fpdfview.h"
#include "fpdf_save.h"int main()
{// 打开加密的PDF文件FPDF_DOCUMENT do

相关文章：

第五课：C++实现加密PDF文档解密

请注意，未经授权的加密PDF文件解密是非法的，本文仅为学术和研究目的提供参考。 打开加密的PDF文件并获取密钥 在C++中，可以使用pdfium库打开加密的PDF文件。使用pdfium库中的FPDF_LoadCustomDocument函数可以打开具有自定义访问权限的加密文件。该函数接受一个IFX_FileRead*…...

编程日记 2023/9/5 21:06:16

罗马数字转整数

罗马数字转整数 题目: 罗马数字包含以下七种字符: I&#xff0c; V&#xff0c; X&#xff0c; L&#xff0c;C&#xff0c;D 和 M。字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M …...

编程日记 2023/9/5 21:05:15

processflow流程图多人协作预热

前言 在线上办公如火如荼的今天&#xff0c;多人协作功能是每个应用绕不开的门槛。processflow在线流程图&#xff08;前身基于drawio二次开发&#xff09;沉寂两年之久&#xff0c;经过长时间设计开发&#xff0c;调整&#xff0c;最终完成了多人协作的核心模块设计。废话不多…...

编程日记 2023/9/5 21:04:14

PCL点云处理之快速计算多个点到同一直线的距离（二百零五）

PCL点云处理之快速计算多个点到同一直线的距离（二百零五） 一、算法简介二、具体实现1.代码2.结果一、算法简介 点到直线的距离计算，是一种常用的算法，在点云处理中，经常遇到需要计算多个点云到同一条直线的距离计算需求，此时若是逐点计算将耗费大量的时间，熟悉点到直线…...

编程日记 2023/9/5 21:03:13

xxl-job 任务调度搭建及简单使用

xxl-job是开源架构&#xff0c;可以通过它实现调度中心和执行器。 git地址和 官网中进行了详细的技术说明。   xxl-job支持单机部署和集群式部署&#xff0c;在集群式部署中又可以实现调度中心集群式部署和执行器集群式部署。本文主要针对调度中心和执行器分离单机部署方式进…...

编程日记 2023/9/5 21:02:12

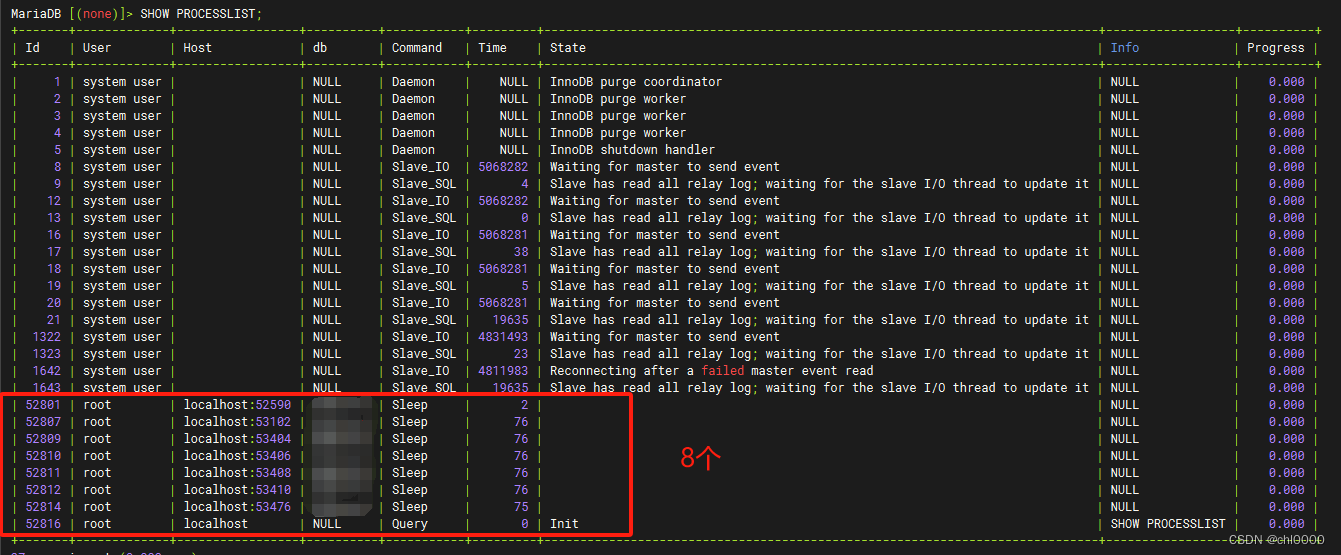
mysql数据库使用技巧整理

查看当前数据库已建立的client连接 > SHOW VARIABLES LIKE max_connections; -- 查看数据库允许的最大连接数&#xff0c;不是实时正在使用的连接数 > SHOW STATUS LIKE Threads_connected; -- 查看当前数据库client的连接数 > SHOW PROCESSLIST; -- 查看具体的连接...

编程日记 2023/9/5 21:01:10

车规微控制器的ECC机制及EMU外设

车规微控制器的ECC机制及EMU外设 文章目录 车规微控制器的ECC机制及EMU外设引言ECC的基本原理ECC RAM的访问方式ECC RAM的初始化SRAM ECC错误注入及EMU外设Flash ECC校验参考文献 引言 ECC是微控制器系统中&#xff0c;用于保障信息安全的常用机制&#xff0c;主要是避免存储设…...

编程日记 2023/9/5 21:00:09

Less的强大变量用法

less中的变量应用十分强大&#xff0c;可以灵活的应用到各种不同需求的场景。 一&#xff0c;属性值变量 声明&#xff1a;sass声明变量是用$符号&#xff0c;而less声明变量是用符号 作用域&#xff1a;也区分为全局变量和局部变量&#xff0c;如果引用的变量有定义局部变量&…...

编程日记 2023/9/5 20:59:08

【相机标定】opencv python 标定相机内参时不计算 k3 畸变参数

文章目录 1. 背景2. 完整的 opencv python 标定相机内参过程3. 选择是否计算畸变参数 k3 1. 背景 畸变参数 k3 通常用于描述径向畸变的更高阶效应&#xff0c;即在需要高精度的应用中可以用到&#xff0c;一般的应用中 k1, k2 足矣。 常见的应用中&#xff0c; orbslam3 中是否…...

编程日记 2023/9/5 20:58:07

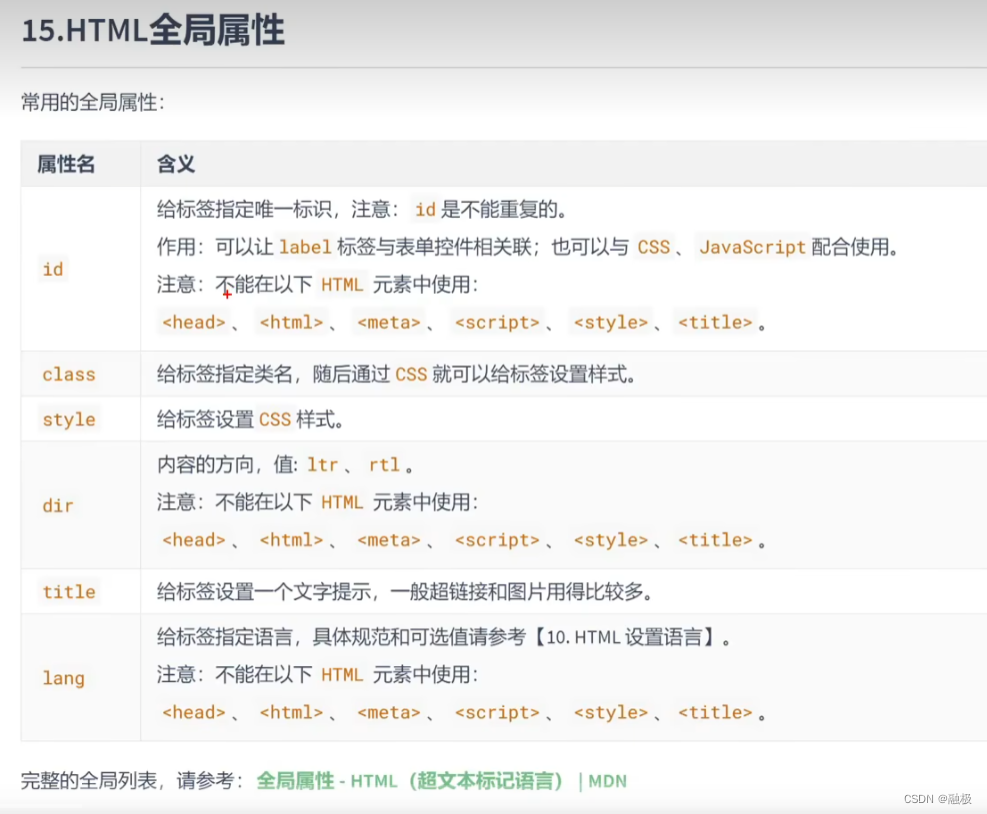
html 标签简介

概述 标签的效果不重要&#xff0c;重要的是标签的语义。 文本标签 文本标签用于包裹&#xff1a;词汇、短语等。排版标签&#xff0c;比如div,p,h1等。排版标签更宏观&#xff08;大段的文字&#xff09;&#xff0c;文本标签更微观&#xff08;词汇、短语&#xff09;。文…...

编程日记 2023/9/5 20:57:05

dos汇编总结

前言&#xff1a; 计组课本需要学习汇编&#xff0c;可惜自己看不太懂。这里发现一个学习方法交给大家。其实新手可能一些抽象表示难理解&#xff0c;这里我把我学习的疑问点以及思路记录一下。 要点&#xff1a; 这里我以题为例给大家分析 输出输入对应大写字母的小写字母 …...

编程日记 2023/9/5 20:56:04

四川玖璨电子商务有限公司：短视频有什么运营

根据短视频有什么运营&#xff0c;短视频的拍摄工具多种多样。无论是在手机上拍摄还是使用专业摄影设备&#xff0c;拍摄短视频的目的都是为了吸引观众的注意力和提升内容的质量。从小花费到高投入&#xff0c;在不断发展的短视频行业中&#xff0c;拍摄方法也得到了不断创新和…...

编程日记 2023/9/5 20:55:03

混合查询多家快递,快速掌握物流信息

在现代社会&#xff0c;快递服务已成为我们日常生活的重要组成部分。无论是购物还是文件传递&#xff0c;我们都需要快递服务的帮助。然而&#xff0c;不同的快递公司需要不同的查询方法&#xff0c;这无疑增加了我们的查询难度。因此&#xff0c;有没有一种方法可以让我们一次…...

编程日记 2023/9/5 20:54:00

独立站新手引流，谷歌SEO工具汇总

俗话说“工欲善其事&#xff0c;必先利其器”&#xff0c;做谷歌SEO也一样&#xff0c;要想做好并提升SEO效果&#xff0c;卖家就需要了解并利用好SEO工具。那我们今天就来盘点一下&#xff0c;常用的SEO工具有哪些吧~ 网站检测工具 1、PageSpeed Insights&#xff1a;这是谷…...

编程日记 2023/9/5 20:52:58

SpringMvc 与 Lombok 碰撞导致 JSON 反序列化失败

SpringMvc 与 Lombok 中 JSON 反序列化失败 错误复现_1 Data public class User{private Long id;private boolean isOk; }RequestMapping public R<User> getUser(RequestBody User user){return R.success(user); }// 前端传参 - {"id": 123456789,"i…...

编程日记 2023/9/5 20:51:57

怎么样显卡叠加，什么是NVIDIA 显卡 非公、公版、涡轮卡

1、显存叠加的问题&#xff0c;因为这个跟是否是深度学习无关&#xff1a; 先说一下显存叠加的问题&#xff0c;因为这个跟是否是深度学习无关&#xff1a;一台机器有多张显卡&#xff0c;显存不会叠加&#xff01;显卡里面包含了显存、cache、计算单元、通信等&#xff0c;每…...

编程日记 2023/9/5 20:50:56

CentOS安装Elasticsearch集群

前言 之前使用的ES集群是其他公司维护&#xff0c;没有机会安装&#xff0c;后来做其他项目&#xff0c;终于有机会安装ES集群&#xff0c;简单记录一下备用 一、安装jdk 安装jdk1.8就可以&#xff0c;可以参考另一篇文章&#xff0c;这里就不细说了 二、修改系统参数 如果在…...

编程日记 2023/9/5 20:49:55

计算机专业毕业生指南

在大四毕业时&#xff0c;完成计算机毕业设计需要一定的计划和组织。以下是一些建议&#xff0c;帮助你在三个月内快速完成毕业设计&#xff1a; 选择一个合适的主题&#xff1a; 选择一个你感兴趣的主题&#xff0c;这将激发你的热情&#xff0c;使你更有动力完成项目。 确保…...

编程日记 2023/9/5 20:48:54

Springboot集成Docker并将镜像推送linux服务器

案例使用springboot项目&#xff0c;在IDEA 中集成Docker生成镜像&#xff0c;并将镜像发布到linux服务器 具体步骤如下&#xff1a; 1、Centos7安装Docker 更新系统的软件包列表 sudo yum update安装Docker所需的软件包和依赖项&#xff1a; sudo yum install docker完成…...

编程日记 2023/9/5 20:47:53

数字孪生与GIS：智慧城市的未来之路

数字孪生和地理信息系统&#xff08;GIS&#xff09;是两个在现代科技中崭露头角的概念&#xff0c;它们的融合为智慧城市项目带来了革命性的机会。本文将解释数字孪生为何需要融合GIS&#xff0c;并以智慧城市项目为例进行说明。 数字孪生是一种虚拟模型&#xff0c;它精确地…...

编程日记 2023/9/5 20:46:52

S2-Pro卷积神经网络（CNN）可视化教学：原理详解与模型部署

S2-Pro卷积神经网络&#xff08;CNN&#xff09;可视化教学&#xff1a;原理详解与模型部署 1. 当AI遇见深度学习教学 想象一下&#xff0c;当你第一次接触卷积神经网络时&#xff0c;是不是被那些抽象的概念和复杂的数学公式搞得晕头转向&#xff1f;传统的学习方式往往需要…...

编程新知 2026/4/4 9:04:47

如何用XUnity.AutoTranslator实现Unity游戏实时翻译：新手完全指南

如何用XUnity.AutoTranslator实现Unity游戏实时翻译&#xff1a;新手完全指南 【免费下载链接】XUnity.AutoTranslator 项目地址: https://gitcode.com/gh_mirrors/xu/XUnity.AutoTranslator 你是否曾经因为语言障碍而错过精彩的Unity游戏&#xff1f;XUnity.AutoTrans…...

编程新知 2026/4/4 8:16:20

ComfyUI-Manager下载加速技术全解析：3种方案实现8倍效率提升的低难度指南

ComfyUI-Manager下载加速技术全解析&#xff1a;3种方案实现8倍效率提升的低难度指南 【免费下载链接】ComfyUI-Manager ComfyUI-Manager is an extension designed to enhance the usability of ComfyUI. It offers management functions to install, remove, disable, and en…...

编程新知 2026/4/4 7:54:12

SDMatte与CI/CD集成：实现模型服务的自动化部署与更新

SDMatte与CI/CD集成&#xff1a;实现模型服务的自动化部署与更新 1. 引言&#xff1a;当AI模型遇上DevOps 最近遇到一个挺有意思的场景&#xff1a;某设计团队在使用SDMatte进行图像背景去除时&#xff0c;每次模型更新都需要手动重新部署服务&#xff0c;导致新功能上线延迟…...

编程新知 2026/4/4 6:53:46

抗体研发核心工具测评：酵母 / 噬菌体文库与展示技术

一、技术定位&#xff1a;生物治疗抗体研发的基石工具单克隆抗体&#xff08;mAbs&#xff09;及其衍生物是生物治疗领域的核心支柱&#xff0c;尤其在肿瘤、自身免疫病等疾病治疗中占据不可替代的地位。抗体研发的起始阶段 —— 抗原特异性抗体筛选&#xff0c;直接决定治疗性…...

编程新知 2026/4/4 6:17:33

【好靶场】越权获取信息

访问页面是一个个人信息页面我们看下雪瞳&#xff0c;可以看到的2个API接口直接抓包发现是可以进行水平越权直接进行intruder得到flag...

编程新知 2026/4/4 5:31:06

别再直接求逆了！用MATLAB的Cholesky分解高效求解对称正定矩阵的逆（附完整代码）

高效求解对称正定矩阵逆&#xff1a;MATLAB中Cholesky分解的工程实践指南 在工程计算领域&#xff0c;对称正定矩阵的逆矩阵求解是一个基础但至关重要的操作。从金融风险模型的协方差矩阵求逆&#xff0c;到机器学习中高斯过程回归的核矩阵运算&#xff0c;再到信号处理中的自适…...

编程新知 2026/4/4 5:10:57

OpenClaw数据可视化：Qwen3-32B分析CSV文件并生成图表报告

OpenClaw数据可视化&#xff1a;Qwen3-32B分析CSV文件并生成图表报告 1. 为什么需要自动化数据分析 上周我接手了一个紧急任务&#xff1a;分析过去半年的销售数据并生成可视化报告。当我手动处理完第三个CSV文件时&#xff0c;突然意识到——这种重复性工作正是AI最擅长的领…...

编程新知 2026/4/4 5:10:57

GLM-OCR GPU算力优化实践：vLLM推理加速+令牌下采样，吞吐提升2.3倍

GLM-OCR GPU算力优化实践&#xff1a;vLLM推理加速令牌下采样&#xff0c;吞吐提升2.3倍 1. 项目背景与优化需求 GLM-OCR是一个基于GLM-V编码器-解码器架构构建的多模态OCR模型&#xff0c;专门为复杂文档理解而设计。这个模型集成了在大规模图文数据上预训练的CogViT视觉编码…...

编程新知 2026/4/4 4:09:59

OpenClaw任务链设计：千问3.5-35B-A3B-FP8复杂流程自动化

OpenClaw任务链设计&#xff1a;千问3.5-35B-A3B-FP8复杂流程自动化 1. 为什么需要任务链自动化 上周我遇到一个典型的工作场景&#xff1a;需要从20份PDF报告中提取关键数据&#xff0c;整理成Excel表格&#xff0c;再根据这些数据生成分析图表&#xff0c;最后通过邮件发送…...

编程新知 2026/4/4 4:05:58