day35 | 860.柠檬水找零、406.根据身高重建队列、452. 用最少数量的箭引爆气球
目录:
解题及思路学习
860. 柠檬水找零
在柠檬水摊上,每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。
每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零,也就是说净交易是每位顾客向你支付 5 美元。
注意,一开始你手头没有任何零钱。
给你一个整数数组 bills ,其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零,返回 true ,否则返回 false 。
示例 1:
输入:bills = [5,5,5,10,20]
输出:true
思考:对于bills,如果支付的为5,则刚好。如果支付的为10,则找5,如果支付20,则可以找一个10,一个5 或者 三个5。所以,尽可能找零大的钱币。
局部最优:遇到账单20,优先消耗美元10,完成本次找零。全局最优:完成全部账单的找零。
class Solution {
public:bool lemonadeChange(vector<int>& bills) {int five = 0, ten = 0, twenty = 0;for (int bill : bills) {if (bill == 5) five++;else if (bill == 10) {if (five <= 0 ) return false;five--;ten++;}else {if (ten > 0 && five > 0) {ten--;five--;twenty++;}else if (five >= 3) {five -= 3;twenty++;}else return false;}}return true;}
};
- 时间复杂度: O(n)
- 空间复杂度: O(1)
遇到感觉没有思路的题目,可以静下心来把能遇到的情况分析一下,只要分析到具体情况了,一下子就豁然开朗了。
406. 根据身高重建队列
假设有打乱顺序的一群人站成一个队列,数组 people 表示队列中一些人的属性(不一定按顺序)。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ,前面 正好 有 ki 个身高大于或等于 hi 的人。
请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ,其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性(queue[0] 是排在队列前面的人)。
示例 1:
输入:people = [[7,0],[4,4],[7,1],[5,0],[6,1],[5,2]]
输出:[[5,0],[7,0],[5,2],[6,1],[4,4],[7,1]]
思考:如果身高相同,那么后面一个数字大的排在后面。如果后面数字相同,则身高越低的排在前面。
在按照身高从大到小排序后:
局部最优:优先按身高高的people的k来插入。插入操作过后的people满足队列属性
全局最优:最后都做完插入操作,整个队列满足题目队列属性
class Solution {static bool cmp(const vector<int>& a, const vector<int>& b) {if (a[0] == b[0]) return a[1] < b[1];return a[0] > b[0];}public:vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {sort(people.begin(), people.end(), cmp);list<vector<int>> que;for (int i = 0; i < people.size(); i++) {int position = people[i][1];std::list<vector<int>>::iterator it = que.begin();while(position--) {it++;}que.insert(it, people[i]);}return vector<vector<int>>(que.begin(), que.end());}
};
- 时间复杂度:O(nlog n + n^2)
- 空间复杂度:O(n)
遇到两个维度权衡的时候,一定要先确定一个维度,再确定另一个维度。
如果两个维度一起考虑一定会顾此失彼。
452. 用最少数量的箭引爆气球
有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ,其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。
一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后,可以无限地前进。
给你一个数组 points ,返回引爆所有气球所必须射出的 最小 弓箭数 。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]]
输出:2
思考:先对数组进行排序,之后遍历过程中,将两个区间合并成一个区间。从第二区区间开始遍历,如果前一个区间的最右边值小于该区间的最左值,则需要一个弓箭。否则,更新当前区间和前一个区间合并后的最右值。
局部最优:当气球出现重叠,一起射,所用弓箭最少。全局最优:把所有气球射爆所用弓箭最少。
class Solution {static bool cmp(const vector<int>& a, const vector<int>& b) {if (a[0] == b[0]) return a[1] < b[1];return a[0] < b[0];}
public:int findMinArrowShots(vector<vector<int>>& points) {sort(points.begin(), points.end(), cmp);int result = 1;for (int i = 1; i < points.size(); i++) {if (points[i - 1][1] < points[i][0]) result++;else if (points[i - 1][1] >= points[i][0]) {points[i][1] = min(points[i - 1][1], points[i][1]);}}return result;}
};
- 时间复杂度:O(nlog n),因为有一个快排
- 空间复杂度:O(1),有一个快排,最差情况(倒序)时,需要n次递归调用。因此确实需要O(n)的栈空间
复盘总结
个人反思
1、区间问题,很多都可以想想是不是需要进行先排序再处理。
2、遇到两个维度权衡的时候,一定要先确定一个维度,再确定另一个维度。
如果两个维度一起考虑一定会顾此失彼。
3、遇到感觉没有思路的题目,可以静下心来把能遇到的情况分析一下,只要分析到具体情况了,一下子就豁然开朗了。
相关文章:

day35 | 860.柠檬水找零、406.根据身高重建队列、452. 用最少数量的箭引爆气球
目录: 解题及思路学习 860. 柠檬水找零 在柠檬水摊上,每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品,(按账单 bills 支付的顺序)一次购买一杯。 每位顾客只买一杯柠檬水,然后向你付 5 美元、10 美…...

ffmpeg批量转码
新建.bat文件 echo offfor %%s in (*.mp4) do ( echo %%s ffmpeg -i %%s -b 7M %%~ns7m.mp4 ) pause如果你的电脑有显卡,也可以使用硬件转码。转码程序链接...

时序预测 | MATLAB实现基于QPSO-BiLSTM、PSO-BiLSTM和BiLSTM时间序列预测
时序预测 | MATLAB实现基于QPSO-BiLSTM、PSO-BiLSTM和BiLSTM时间序列预测 目录 时序预测 | MATLAB实现基于QPSO-BiLSTM、PSO-BiLSTM和BiLSTM时间序列预测效果一览基本描述程序设计参考资料 效果一览 基本描述 1.Matlab实现QPSO-BiLSTM、PSO-BiLSTM和BiLSTM神经网络时间序列预测…...
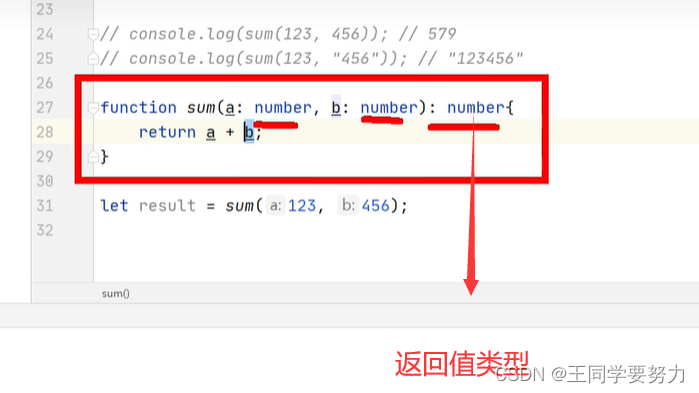
【TypeScript学习】—基本类型(二)
【TypeScript学习】—基本类型(二) 一、TypeScript基本类型 //也可以直接用字面量进行类型声明let a:10; a10;//也可以使用 |来连接多个类型(联合类型)let b:"male"|"female"; b"male"; b"fe…...

uni-app点击复制指定内容(点击复制)
官方api uni.setClipboardData(OBJECT) uni.setClipboardData({data: 要被复制的内容,success: function () {console.log(success);} });...

无涯教程-Flutter - 简介
Flutter是一个由谷歌开发的开源移动应用软件开发工具包,用于为Android、iOS、 Windows、Mac、Linux、Google Fuchsia开发应用。 通常,创建移动应用程序是一个非常复杂和具有挑战性的任务。有许多框架可用,它提供了开发移动应用程序的出色函数…...
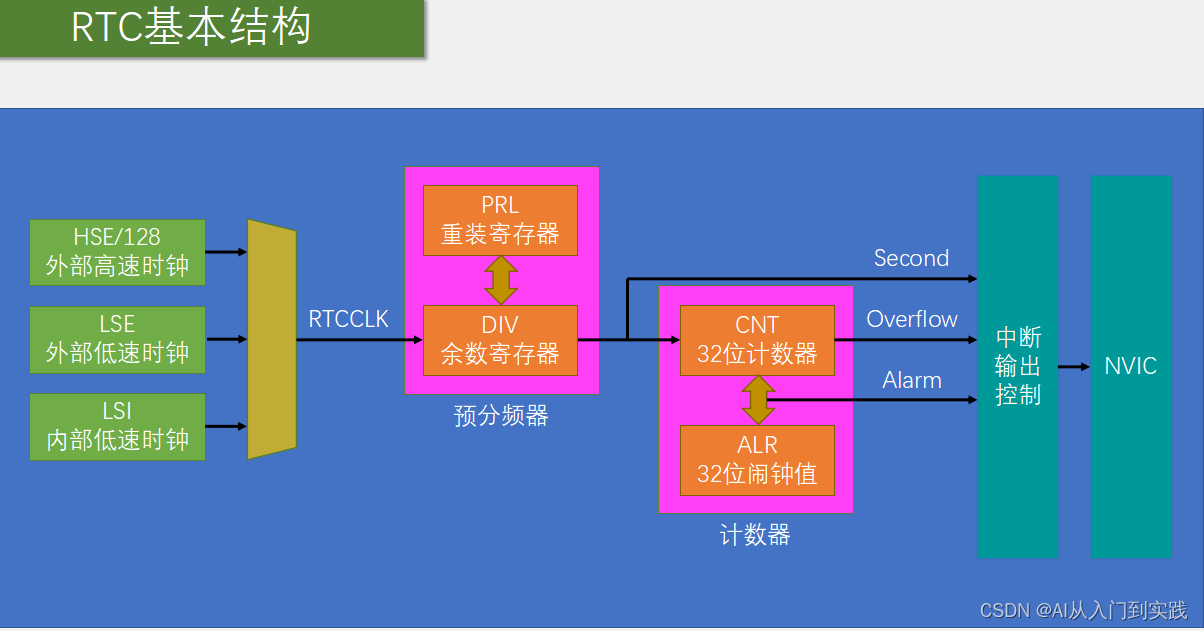
【STM32】学习笔记-时间戳RTC
Unix时间戳 Unix 时间戳(Unix Timestamp)定义为从UTC/GMT的1970年1月1日0时0分0秒开始所经过的秒数,不考虑闰秒 时间戳存储在一个秒计数器中,秒计数器为32位/64位的整型变量 世界上所有时区的秒计数器相同,不同时区通…...

绿色能源迎来跨越式增长新时代
当今世界,百年未有之大变局加速演进,新一轮科技革命和产业变革深入发展,全球气候治理呈现新局面,新能源和信息技术紧密融合,生产生活方式加快转向低碳化、智能化,能源体系和发展模式正在进入非化石能源主导…...

【算法】函数渐近的界基础知识及定理
创作不易,本篇文章如果帮助到了你,还请点赞 关注支持一下♡>𖥦<)!! 主页专栏有更多知识,如有疑问欢迎大家指正讨论,共同进步! 🔥c系列专栏:C/C零基础到精通 🔥 给大…...

stable diffusion实践操作-writing
文章目录 前言一、优点1.1、免费开源1.2、拥有强大的外接模型 二、组成要素2.1 底模2.2 风格2.3 提示词2.4 参数配置 三、生图原理四、下载链接 实践正文一、安装1.1 电脑硬件配置查看1.2 安装本地版本的stable diffusion1.3 SD使用教程 二、模型介绍与下载2.1大模型2.2 Lora模…...
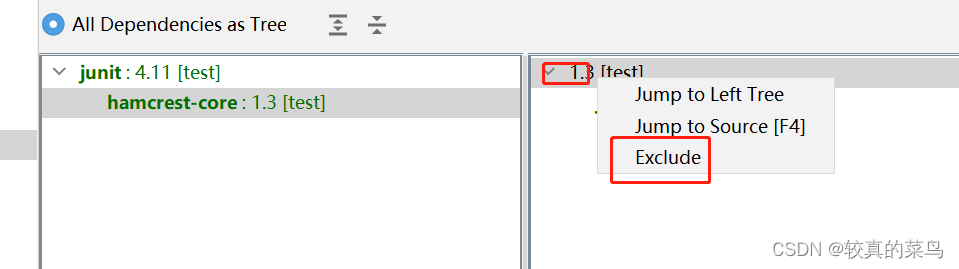
idea查找maven所有依赖
文章目录 idea自带的依赖结构图idea安装maven helper插件 idea自带的依赖结构图 缺点是只有依赖,没有版本 idea安装maven helper插件 settings–>plugins–>搜索maven helper并安装 安装后打开pom.xml文件会有依赖解析 勾选conflict就是有冲突的依赖选中…...
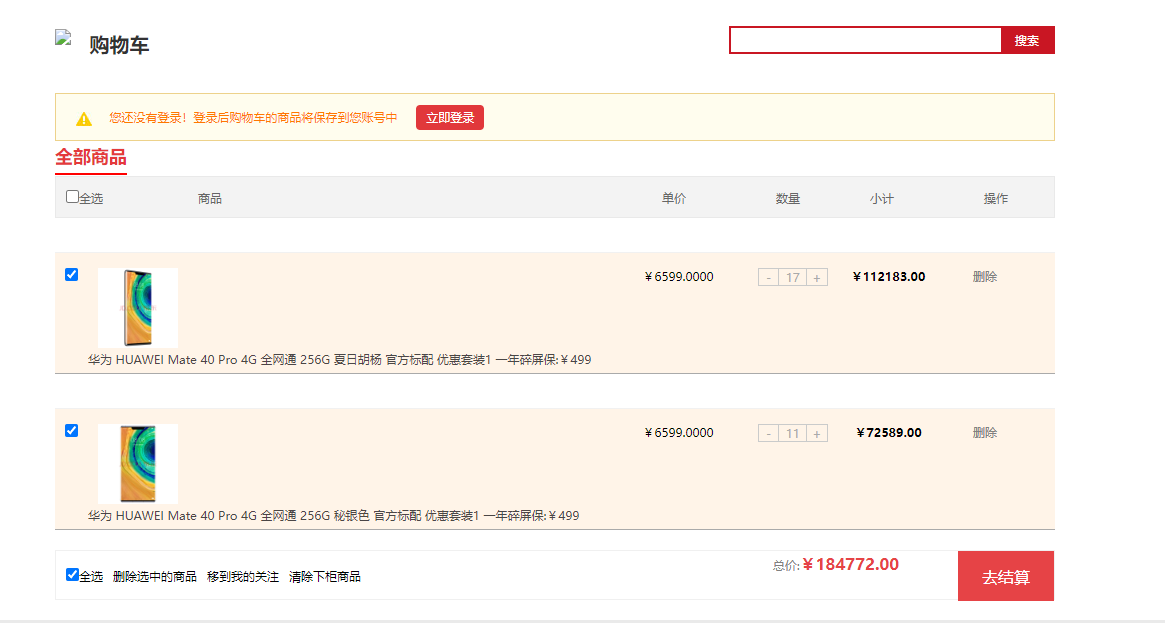
【业务功能篇97】微服务-springcloud-springboot-电商购物车模块-获取当前登录用户的购物车信息
购物车功能 一、购物车模块 1.创建cart服务 我们需要先创建一个cart的微服务,然后添加相关的依赖,设置配置,放开注解。 <dependencies><dependency><groupId>com.msb.mall</groupId><artifactId>mall-commo…...

Shell常用的几个正则表达式:[:alnum:], [:alpha:], [:upper:], [:lower:], [:digit:] 认知
一:通配符命令简介: 匹配符合相关条件的符号,匹配文件名查找。 通配符类型: *:匹配任意长度的任意字符 ?:匹配任意单个字符 []:匹配指定范围内的任意单个字符 [^]:匹配指…...
简单的爬虫代码 爬(豆瓣电影)
路漫漫其修远兮,吾将上下而求索 这次写一个最简单的python爬虫代码,也是大多教程第一次爬取的,代码里面有个别的简单介绍,希望能加深您对python爬虫的理解。 本次爬取两个网页数据 一 爬取的网站 豆瓣电影 爬取网页中的&#…...
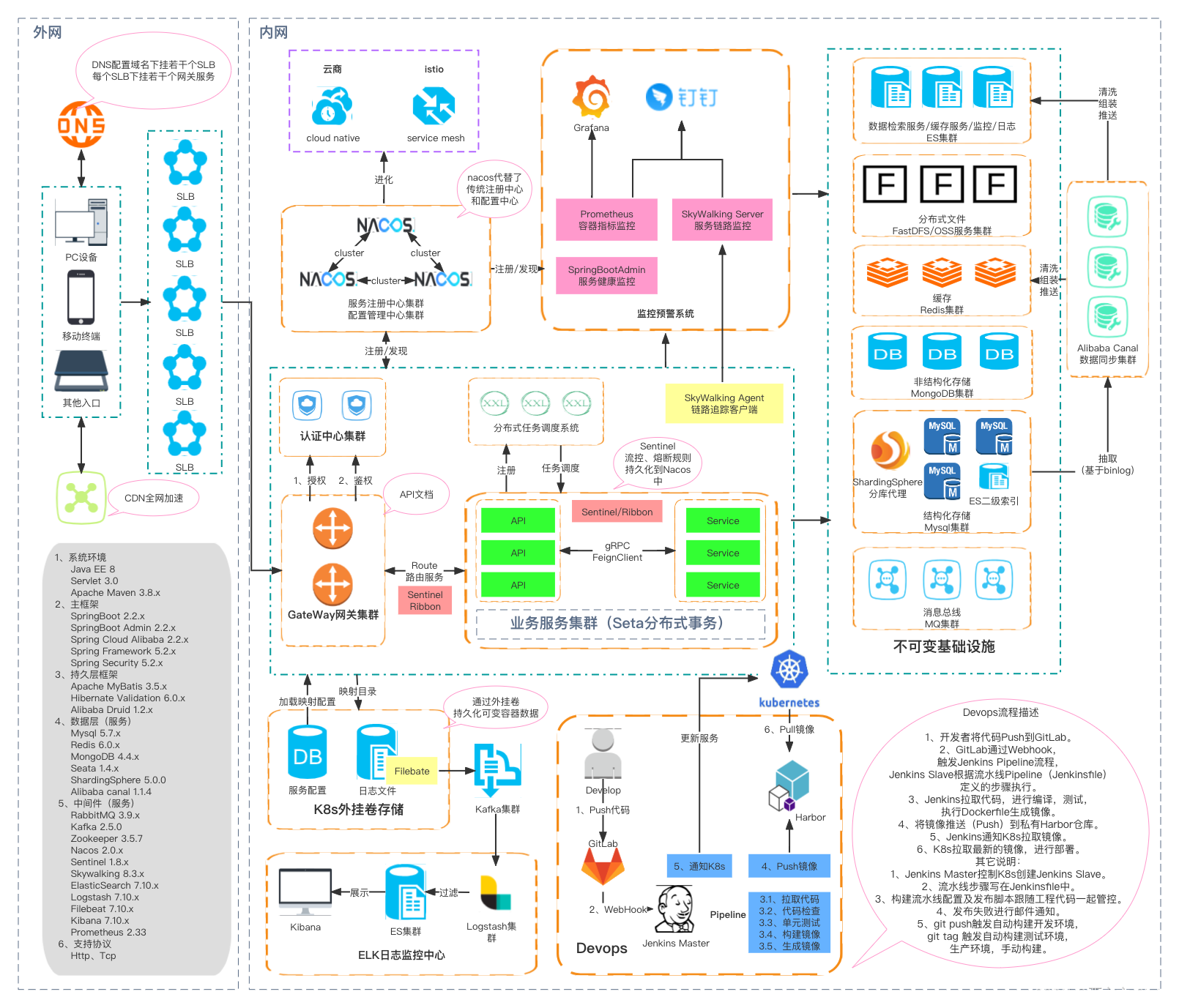
微服务之架构演变
随着互联网的发展,网站应用规模不断扩大,网站架构随之不断演变,演变历史大致分为单体应用架构-垂直应用架构-分布式架构-SOA架构-微服务架构-云原生架构 架构演变 单体应用架构 以前网站流量小,只需要一个应用就可以把所有功能…...
)
面试问题记录一 --- C++(Qt方向)
以下是我于2023年6~7月间换工作时遇到的面试题目,有需要的小伙伴可以参考下。约100个题目。 1 C和C++的区别 1) 文件区别:C源文件后缀 .c;C++源文件后缀 .cpp 2) 返回值: C默认返回int型;C++ 若无返回值,必须指定为void 3) 参数列表:C默认接收多个…...
测试提取图像的特征点和聚类中心)
使用词袋模型(BoW)测试提取图像的特征点和聚类中心
文章目录 环境配置代码测试 环境配置 (1) 导入opencv,参考链接 https://blog.csdn.net/Aer_7z/article/details/132612369(2) 安装numpy 激活虚拟环境的前提下,输入: pip install numpy(3) 安装sklearn 激活虚拟环境的前提下,输…...
利用vba处理Excel表格数据实现键值转化,适用于将编码转化成对应的文本
最近遇到了一个甲方需要提供系统登录的用户名单和对应的角色权限内容。无奈直接从数据库导出的数据对应的都是编码,没有转成中文,想着偷个懒能不能直接用Excel直接转,网上看了一下有修改单元格格式的,但需要编码是2到3个。多的就用…...
IntelliJ IDEA(Windows 版)的所有快捷键
🪁🍁 希望本文能够给您带来一定的帮助🌸文章粗浅,敬请批评指正!🍁🐥 大家好 本文参考了 IntelliJ IDEA 的官网,列举了IntelliJ IDEA(Windows 版)的所有快捷…...

文件上传漏洞全面渗透姿势
0x00 文件上传场景 (本文档只做技术交流) 文件上传的场景真的随处可见,不加防范小心,容易造成漏洞,造成信息泄露,甚至更为严重的灾难。 比如某博客网站评论编辑模块,右上角就有支持上传图片的功能,提交带…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
