ML@矩阵微积分基础
文章目录
- 矩阵微积分@Matrix calculus
- 记法
- 简单Jacobi Matrix
- 分子记法
- 分母记法
- 一般形式的Jacobi Matrix
- Types of matrix derivative
- 向量求导
- 向量对标量求导
- 标量对向量求导
- 向量对向量求导
- 矩阵求导
- 矩阵对标量求导(切矩阵)
- 标量对矩阵求导
- 记法
- 向量求导
- 向量对标量求导
- 标量对向量求导
- 向量对向量求导
- 矩阵求导
- 矩阵对标量求导
- 标量对矩阵求导
矩阵微积分@Matrix calculus
- 深度学习中的矩阵微积分学 - Dezeming Family https://dezeming.top › uploads › 2022/02 › 深度…
- 矩阵论 第2版_图书搜索 (superlib.net)
- **作者:**方保镕,周继东,李医民编著 **页数:**401 **出版社:**北京:清华大学出版社 **出版日期:**2013.12
- 简介:本书比较全面、系统地介绍了矩阵的基本理论、方法及其应用。
- 全书分上、下两篇,上篇为基础篇,下篇为应用篇。
- Matrix calculus - Wikipedia
- 矩阵微积分 (wikipedia.org)
记法
- 在表示向量和矩阵时,通过用单个变量(字母)来表示许多变量的方式,把矩阵记法的效用发挥到最大。
- 可以用不同字体来区分标量、向量和矩阵。
- 我们使用M(n,m)M(n,m)M(n,m)来表示包含n行m列的n×mn×mn×m实矩阵的空间。
- 该空间中的一般矩阵用大写字母表示,例如A,X,Y等。
- 而若该矩阵属于M(n,1)M(n,1)M(n,1),即列向量,则用粗体小写字母表示,如a,x,y等。(但有时为例放便,不以粗体书写)
- 特别地,M(1,1)中的元素为标量,用小写斜体字母表示,如a,t,x等。
- XTX^TXT 表示矩阵转置,tr(X)tr(X)tr(X)表示矩阵的迹,而 det(X)\det(X)det(X)或∣X∣|X|∣X∣表示行列式。
- 除非专门注明,所有函数都默认属于光滑函数。
- 通常字母表前半部分的字母(a,b,c,…)(a, b, c, …)(a,b,c,…)用于表示常量
- 而后半部分的字母(t,x,y,…)(t, x, y, …)(t,x,y,…)用于表示变量。
- 变量可以是标量,也可以是向量
- 标量可能是常数,也可能是变量
简单Jacobi Matrix
分子记法
-
这个矩阵我们称为雅克比矩阵 (Jacobian matrix),一下是分子记法(分子布局 (numerator layout))
-
J=[∇f(x,y)∇g(x,y)]=[∂f(x,y)∂x∂f(x,y)∂y∂g(x,y)∂x∂g(x,y)∂y]\mathcal{J}=\left[\begin{array}{l} \nabla f(x, y) \\ \nabla g(x, y) \end{array}\right]=\left[\begin{array}{ll} \frac{\partial f(x, y)}{\partial x} & \frac{\partial f(x, y)}{\partial y} \\ \frac{\partial g(x, y)}{\partial x} & \frac{\partial g(x, y)}{\partial y} \end{array}\right] J=[∇f(x,y)∇g(x,y)]=[∂x∂f(x,y)∂x∂g(x,y)∂y∂f(x,y)∂y∂g(x,y)]
分母记法
-
-
有许多著作和软件会使用分母布局 (denominator layout),其实这就是分子布局的矩阵转置:
- [∂f(x,y)∂x∂f(x,y)∂y∂g(x,y)∂x∂g(x,y)∂y]T=[∂f(x,y)∂x∂g(x,y)∂x∂f(x,y)∂y∂g(x,y)∂y]\left[\begin{array}{ll} \frac{\partial f(x, y)}{\partial x} & \frac{\partial f(x, y)}{\partial y} \\ \frac{\partial g(x, y)}{\partial x} & \frac{\partial g(x, y)}{\partial y} \end{array}\right]^{T}=\left[\begin{array}{ll} \frac{\partial f(x, y)}{\partial x} & \frac{\partial g(x, y)}{\partial x} \\ \frac{\partial f(x, y)}{\partial y} & \frac{\partial g(x, y)}{\partial y} \end{array}\right] [∂x∂f(x,y)∂x∂g(x,y)∂y∂f(x,y)∂y∂g(x,y)]T=[∂x∂f(x,y)∂y∂f(x,y)∂x∂g(x,y)∂y∂g(x,y)]
一般形式的Jacobi Matrix
-
对于多个标量函数,讲它们组合到一个向量中:
-
令y=f(x)\mathbf{y}=\mathbf{f(x)}y=f(x)是一个由若干(设为m个)多元(设为n元)标量函数构成的向量
-
把n维向量x\mathbf{x}x作为输入,fi(x)f_i(\mathbf{x})fi(x)返回一个标量值(Rn→RR^n\to{R}Rn→R)
-
y=(y1y2⋮ym)=f(x)=(f1(x)f2(x)⋮fm(x))\mathbf{y}=\begin{pmatrix} y_{1}\\ y_{2}\\ \vdots\\ y_{m}\\ \end{pmatrix} =\mathbf{f(x)} =\begin{pmatrix} f_{1}(\mathbf{x})\\ f_{2}(\mathbf{x})\\ \vdots\\ f_{m}(\mathbf{x})\\ \end{pmatrix} y=y1y2⋮ym=f(x)=f1(x)f2(x)⋮fm(x)
-
m=nm=nm=n的情况是很常见的
-
Jacobi矩阵就是与x\mathbf{x}x函数相关的的m个梯度
-
∂y∂x=(∇f1(x)∇f2(x)⋮∇fm(x))=(∂∂xf1(x)∂∂xf2(x)⋮∂∂xfm(x))=(∂∂x1f1(x)∂∂x2f1(x)⋯∂∂xnf1(x)∂∂x1f2(x)∂∂x2f2(x)⋯∂∂xnf2(x)⋮∂∂x1fm(x)∂∂x2fm(x)⋯∂∂xnfm(x))m×nX∈Rn∇fi(x)=∂∂xfi(x)=[∂∂x1fi(x),∂∂x2fi(x),⋯,∂∂xnfi(x)]\frac{\partial\mathbf{y}}{\partial{\mathbf{x}}} =\begin{pmatrix} \nabla f_{1}{(\mathbf{x})}\\ \nabla f_{2}{(\mathbf{x})}\\ \vdots\\ \nabla f_{m}{(\mathbf{x})}\\ \end{pmatrix} =\begin{pmatrix} \frac{\partial}{\partial{\mathbf{x}}}f_{1}(\mathbf{x})\\ \frac{\partial}{\partial{\mathbf{x}}}f_{2}(\mathbf{x})\\ \vdots\\ \frac{\partial}{\partial{\mathbf{x}}}f_{m}(\mathbf{x})\\ \end{pmatrix}\\ =\begin{pmatrix} \frac{\partial}{\partial{{x_1}}}f_{1}(\mathbf{x})& \frac{\partial}{\partial{{x_2}}}f_{1}(\mathbf{x})& \cdots& \frac{\partial}{\partial{{x_n}}}f_{1}(\mathbf{x})\\ \frac{\partial}{\partial{{x_1}}}f_{2}(\mathbf{x})& \frac{\partial}{\partial{{x_2}}}f_{2}(\mathbf{x})& \cdots& \frac{\partial}{\partial{{x_n}}}f_{2}(\mathbf{x})\\ \vdots\\ \frac{\partial}{\partial{{x_1}}}f_{m}(\mathbf{x})& \frac{\partial}{\partial{{x_2}}}f_{m}(\mathbf{x})& \cdots& \frac{\partial}{\partial{{x_n}}}f_{m}(\mathbf{x})\\ \end{pmatrix}_{m\times{n}} \\ \mathbf{X}\in{R^n} \\ \nabla f_{i}{(\mathbf{x})}=\frac{\partial}{\partial{\mathbf{x}}}f_{i}(\mathbf{x}) = [\frac{\partial}{\partial{{x_1}}}f_{i}(\mathbf{x}), \frac{\partial}{\partial{{x_2}}}f_{i}(\mathbf{x}), \cdots, \frac{\partial}{\partial{{x_n}}}f_{i}(\mathbf{x})] ∂x∂y=∇f1(x)∇f2(x)⋮∇fm(x)=∂x∂f1(x)∂x∂f2(x)⋮∂x∂fm(x)=∂x1∂f1(x)∂x1∂f2(x)⋮∂x1∂fm(x)∂x2∂f1(x)∂x2∂f2(x)∂x2∂fm(x)⋯⋯⋯∂xn∂f1(x)∂xn∂f2(x)∂xn∂fm(x)m×nX∈Rn∇fi(x)=∂x∂fi(x)=[∂x1∂fi(x),∂x2∂fi(x),⋯,∂xn∂fi(x)]
-
-
对于 fi(x)=fi([x1,x2,⋯,xn])=xif_i(\mathbf{x})=f_i([x_1,x_2,\cdots,x_n])= x_ifi(x)=fi([x1,x2,⋯,xn])=xi (构成的)的恒等函数 f(x)=x\mathbf{f(x)} = \mathbf{x}f(x)=x,我们可以计算得到它的雅克比矩阵(这里的 m 等于 n)
-
y=f(x)=(f1(x),f2(x),⋯,fn(x))=x\mathbf{y=f(x)}=(f_1(\mathbf{x}),f_2(\mathbf{x}),\cdots,f_n(\mathbf{x}))=\mathbf{x} y=f(x)=(f1(x),f2(x),⋯,fn(x))=x
-
注意这里的函数f\mathbf{f}f是向量输入x\mathbf{x}x,同时向量输出y\mathbf{y}y
- 假设它么的维数分别是n,mn,mn,m,且有m=nm=nm=n
- 对上述恒等函数求jacobi matrix
-
∂y∂x=(∂∂x1f1(x)∂∂x2f1(x)⋯∂∂xnf1(x)∂∂x1f2(x)∂∂x2f2(x)⋯∂∂xnf2(x)⋮∂∂x1fm(x)∂∂x2fm(x)⋯∂∂xnfm(x))m×n=(∂∂x1x1∂∂x2x1⋯∂∂xnx1∂∂x1x2∂∂x2x2⋯∂∂xnx2⋮∂∂x1xm∂∂x2xm⋯∂∂xnxm)m×n=n2=(10⋯001⋯0⋮⋮⋱⋮00⋯1)n×n\frac{\partial\mathbf{y}}{\partial{\mathbf{x}}} =\begin{pmatrix} \frac{\partial}{\partial{{x_1}}}f_{1}(\mathbf{x})& \frac{\partial}{\partial{{x_2}}}f_{1}(\mathbf{x})& \cdots& \frac{\partial}{\partial{{x_n}}}f_{1}(\mathbf{x})\\ \frac{\partial}{\partial{{x_1}}}f_{2}(\mathbf{x})& \frac{\partial}{\partial{{x_2}}}f_{2}(\mathbf{x})& \cdots& \frac{\partial}{\partial{{x_n}}}f_{2}(\mathbf{x})\\ \vdots\\ \frac{\partial}{\partial{{x_1}}}f_{m}(\mathbf{x})& \frac{\partial}{\partial{{x_2}}}f_{m}(\mathbf{x})& \cdots& \frac{\partial}{\partial{{x_n}}}f_{m}(\mathbf{x})\\ \end{pmatrix}_{m\times{n}} \\ =\begin{pmatrix} \frac{\partial}{\partial{{x_1}}}x_1& \frac{\partial}{\partial{{x_2}}}x_1& \cdots& \frac{\partial}{\partial{{x_n}}}x_1\\ \frac{\partial}{\partial{{x_1}}}x_2& \frac{\partial}{\partial{{x_2}}}x_2& \cdots& \frac{\partial}{\partial{{x_n}}}x_2\\ \vdots\\ \frac{\partial}{\partial{{x_1}}}x_m& \frac{\partial}{\partial{{x_2}}}x_m& \cdots& \frac{\partial}{\partial{{x_n}}}x_m\\ \end{pmatrix}_{m\times{n}=n^2} =\begin{pmatrix} 1 &0 &\cdots&0 \\ 0 &1 &\cdots&0 \\ \vdots&\vdots&\ddots&\vdots\\ 0 &0 &\cdots&1 \\ \end{pmatrix}_{n\times{n}} ∂x∂y=∂x1∂f1(x)∂x1∂f2(x)⋮∂x1∂fm(x)∂x2∂f1(x)∂x2∂f2(x)∂x2∂fm(x)⋯⋯⋯∂xn∂f1(x)∂xn∂f2(x)∂xn∂fm(x)m×n=∂x1∂x1∂x1∂x2⋮∂x1∂xm∂x2∂x1∂x2∂x2∂x2∂xm⋯⋯⋯∂xn∂x1∂xn∂x2∂xn∂xmm×n=n2=10⋮001⋮0⋯⋯⋱⋯00⋮1n×n
-
Types of matrix derivative
| Types | Scalar | Vector | Matrix |
|---|---|---|---|
| Scalar | ∂y∂x\frac{\partial y}{\partial x}∂x∂y | ∂y∂x\frac{\partial \mathbf{y}}{\partial x}∂x∂y | ∂Y∂x\frac{\partial \mathbf{Y}}{\partial x}∂x∂Y |
| vector | ∂y∂x\frac{\partial y}{\partial \mathbf{x}}∂x∂y | ∂y∂x\frac{\partial \mathbf{y}}{\partial \mathbf{x}}∂x∂y | |
| Matrix | ∂y∂X\frac{\partial y}{\partial \mathbf{X}}∂X∂y |
向量求导
向量对标量求导
-
由于向量可看成仅有一列的矩阵,最简单的矩阵求导为向量求导。
-
通过如下方式表达大部分向量微积分:
- 把n维向量构成的空间M(n,1)等同为欧氏空间 RnR^nRn, 标量M(1,1)M(1,1)M(1,1)等同于R。
-
向量y=[y1y2⋯ym]T{\displaystyle \mathbf {y} ={\begin{bmatrix}y_{1}&y_{2}&\cdots &y_{m}\end{bmatrix}}^{\mathsf {T}}}y=[y1y2⋯ym]T关于标量 xxx的导数可以(用分子记法)写成
-
yi=yi(x)y_i=y_i(\mathbf{x})yi=yi(x)多元(输入)标量(输出)函数
- i=1,2,⋯,mi=1,2,\cdots,mi=1,2,⋯,m
- 对标量xxx进行广播,再分别求导
-
∂y∂x=[∂y1∂x∂y2∂x⋮∂ym∂x]{\displaystyle {\frac {\partial \mathbf {y} }{\partial x}}={\begin{bmatrix}{\frac {\partial y_{1}}{\partial x}}\\{\frac {\partial y_{2}}{\partial x}}\\\vdots \\{\frac {\partial y_{m}}{\partial x}}\\\end{bmatrix}}} ∂x∂y=∂x∂y1∂x∂y2⋮∂x∂ym
-
-
在向量微积分中,向量y\mathbf {y}y关于标量变量xxx的导数也被称为向量y\mathbf {y}y的切向量(在xxx方向的),∂y∂x{\displaystyle {\frac {\partial \mathbf {y} }{\partial x}}}∂x∂y
-
例子
- 简单的样例包括欧式空间中的速度向量,它是位移向量(看作关于时间的函数)的切向量。
- 更进一步而言, 加速度是速度的切向量。
标量对向量求导
-
标量y对向量x=[x1x2⋯xn]T{\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}&x_{2}&\cdots &x_{n}\end{bmatrix}}^{\mathsf {T}}}x=[x1x2⋯xn]T的导数可以(用分子记法)写成
-
∂y∂x=[∂y∂x1∂y∂x2⋯∂y∂xn]{\displaystyle {\frac {\partial y}{\partial \mathbf {x} }}={\begin{bmatrix}{\frac {\partial y}{\partial x_{1}}}&{\frac {\partial y}{\partial x_{2}}}&\cdots &{\frac {\partial y}{\partial x_{n}}}\end{bmatrix}}}∂x∂y=[∂x1∂y∂x2∂y⋯∂xn∂y]
- 对被求导的多元函数y=y(x)y=y(\mathbf{x})y=y(x)进行广播(broadcasting),再进行求导
-
(∂y∂x)T=(∂y∂x1∂y∂x2∂y∂x3)(\frac{\partial{y}}{\partial{\mathbf{x}}})^T =\begin{pmatrix} \frac {\partial y}{\partial \mathbf {x_1} }\\ \frac {\partial y}{\partial \mathbf {x_2} }\\ \frac {\partial y}{\partial \mathbf {x_3}} \end{pmatrix} (∂x∂y)T=∂x1∂y∂x2∂y∂x3∂y
-
-
在向量微积分中,标量y在的空间RnR^nRn(其独立坐标是x的分量)中的梯度是标量y对向量x的导数的转置。
-
在物理学中,电场是电势的负梯度向量。
-
标量函数f(x)对空间向量x在单位向量u(在这里表示为列向量)方向上的方向导数可以用梯度定义:
-
∇uf(x)=∇f(x)⋅u\displaystyle \nabla _{\mathbf {u} }{f}(\mathbf {x} )=\nabla f(\mathbf {x} )\cdot \mathbf {u}∇uf(x)=∇f(x)⋅u
-
u=(cosα,cosβ,cosγ)u=(\cos\alpha,\cos\beta,\cos\gamma)u=(cosα,cosβ,cosγ),即该单位向量是由u方向的方向余弦构成的
-
∇f(x)u=(∂y∂x1,∂y∂x2,∂y∂x3)⋅(cosα,cosβ,cosγ)=(∂y∂x1∂y∂x2∂y∂x3)(cosα,cosβ,cosγ)=(∂y∂x)Tu\nabla{f(x)}u=(\frac {\partial y}{\partial \mathbf {x_1} },\frac {\partial y}{\partial \mathbf {x_2} },\frac {\partial y}{\partial \mathbf {x_3} }) \cdot(\cos\alpha,\cos\beta,\cos\gamma) \\=\begin{pmatrix} \frac {\partial y}{\partial \mathbf {x_1} }\\ \frac {\partial y}{\partial \mathbf {x_2} }\\ \frac {\partial y}{\partial \mathbf {x_3}} \end{pmatrix}(\cos\alpha,\cos\beta,\cos\gamma) =(\frac{\partial{y}}{\partial{\mathbf{x}}})^T\mathbf{u} ∇f(x)u=(∂x1∂y,∂x2∂y,∂x3∂y)⋅(cosα,cosβ,cosγ)=∂x1∂y∂x2∂y∂x3∂y(cosα,cosβ,cosγ)=(∂x∂y)Tu
- x=(x1,x2,x3)\mathbf x=(x_1,x_2,x_3)x=(x1,x2,x3)
-
-
-
使用刚才定义的标量对向量的导数的记法,可以把方向导数写作 ∇uf=(∂f∂x)⊤u\displaystyle \nabla _{\mathbf {u} }f=\left({\frac {\partial f}{\partial \mathbf {x} }}\right)^{\top }\mathbf {u}∇uf=(∂x∂f)⊤u 这类记法在证明乘法法则和链式法则的时候非常直观,因为它们与我们熟悉的标量导数的形式较为相似。
向量对向量求导
-
前面两种情况可以看作是向量对向量求导在其中一个是一维向量情况下的特例。
-
类似地我们将会发现有关矩阵的求导可被以一种类似的方式化归为向量求导。
-
分量为函数的向量 y=[y1y2⋯ym]T{\displaystyle \mathbf {y} ={\begin{bmatrix}y_{1}&y_{2}&\cdots &y_{m}\end{bmatrix}}^{\mathsf {T}}}y=[y1y2⋯ym]T对输入向量x=[x1x2⋯xn]T{\displaystyle \mathbf {x} ={\begin{bmatrix}x_{1}&x_{2}&\cdots &x_{n}\end{bmatrix}}^{\mathsf {T}}}x=[x1x2⋯xn]T的导数x→yi(x)\mathbf{x}\to{y_i(\mathbf{x})}x→yi(x),可以(用分子记法) 写作
-
Note:yi=yi(x)y_i=y_i(\mathbf{x})yi=yi(x),i=1,2,⋯,mi=1,2,\cdots,mi=1,2,⋯,m
-
这部分在开头做过展示(Jacobi Matrix)
-
∂y∂x=[∂y1∂x1∂y1∂x2⋯∂y1∂xn∂y2∂x1∂y2∂x2⋯∂y2∂xn⋮⋮⋱⋮∂ym∂x1∂ym∂x2⋯∂ym∂xn]{\displaystyle {\frac {\partial \mathbf {y} }{\partial \mathbf {x} }}={\begin{bmatrix}{\frac {\partial y_{1}}{\partial x_{1}}}&{\frac {\partial y_{1}}{\partial x_{2}}}&\cdots &{\frac {\partial y_{1}}{\partial x_{n}}}\\{\frac {\partial y_{2}}{\partial x_{1}}}&{\frac {\partial y_{2}}{\partial x_{2}}}&\cdots &{\frac {\partial y_{2}}{\partial x_{n}}}\\\vdots &\vdots &\ddots &\vdots \\{\frac {\partial y_{m}}{\partial x_{1}}}&{\frac {\partial y_{m}}{\partial x_{2}}}&\cdots &{\frac {\partial y_{m}}{\partial x_{n}}}\\\end{bmatrix}}} ∂x∂y=∂x1∂y1∂x1∂y2⋮∂x1∂ym∂x2∂y1∂x2∂y2⋮∂x2∂ym⋯⋯⋱⋯∂xn∂y1∂xn∂y2⋮∂xn∂ym
- 每一行相当于函数yiy_iyi对向量x\mathbf{x}x求导
- y\mathbf{y}y中包含了n个向量,所以y\mathbf{y}y对x\mathbf{x}x会产生n行,它们构成矩阵∂y∂x\frac{\partial{\mathbf{y}}}{\partial{\mathbf{x}}}∂x∂y
-
向量函数
- 向量值函数,有时也称为向量函数,是一个单变量或多变量的、值域是多维向量或者无穷维向量的集合的函数。向量值函数的输入可以是一个标量或者一个向量(定义域的维度可以是1或大于1);定义域的维度不取决于值域的维度。
- A vector-valued function, also referred to as a vector function, is a mathematical function of one or more variables whose range is a set of multidimensional vectors or infinite-dimensional vectors.
- The input of a vector-valued function could be a scalar or a vector (that is, the dimension of the domain could be 1 or greater than 1);
- the dimension of the function’s domain has no relation to the dimension of its range.
-
-
在向量微积分中,向量函数y对分量表示一个空间的向量x\mathbf{x}x的导数也被称为前推 (微分),或雅可比矩阵。
- In vector calculus, the derivative of a vector function y with respect to a vector x whose components(分量) represent a space is known as the pushforward (or differential), or the Jacobian matrix.
- 在向量微积分中,向量函数y关于向量x的导数(其分量表示空间)被称为推进(或微分),或称为雅克比矩阵。
-
向量函数f\mathbf{f}f对RnR^nRn空间中向量v的前推为df(v)=∂f∂vdv\displaystyle d\,\mathbf {f} (\mathbf {v} )={\frac {\partial \mathbf {f} }{\partial \mathbf {v} }}d\,\mathbf {v}df(v)=∂v∂fdv
矩阵求导
- 有两种类型的矩阵求导可以被写成相同大小的矩阵:矩阵对标量求导和标量对矩阵求导。
- 它们在解决应用数学的许多领域常见的最小化问题中十分有用。
- 类比于向量求导,相应的概念有切矩阵和梯度矩阵。
矩阵对标量求导(切矩阵)
-
矩阵函数Y对标量x的导数被称为切矩阵,(用分子记法)可写成:
- ∂Y∂x=[∂y11∂x∂y12∂x⋯∂y1n∂x∂y21∂x∂y22∂x⋯∂y2n∂x⋮⋮⋱⋮∂ym1∂x∂ym2∂x⋯∂ymn∂x]{\displaystyle {\frac {\partial \mathbf {Y} }{\partial x}}={\begin{bmatrix}{\frac {\partial y_{11}}{\partial x}}&{\frac {\partial y_{12}}{\partial x}}&\cdots &{\frac {\partial y_{1n}}{\partial x}}\\{\frac {\partial y_{21}}{\partial x}}&{\frac {\partial y_{22}}{\partial x}}&\cdots &{\frac {\partial y_{2n}}{\partial x}}\\\vdots &\vdots &\ddots &\vdots \\{\frac {\partial y_{m1}}{\partial x}}&{\frac {\partial y_{m2}}{\partial x}}&\cdots &{\frac {\partial y_{mn}}{\partial x}}\\\end{bmatrix}}} ∂x∂Y=∂x∂y11∂x∂y21⋮∂x∂ym1∂x∂y12∂x∂y22⋮∂x∂ym2⋯⋯⋱⋯∂x∂y1n∂x∂y2n⋮∂x∂ymn
标量对矩阵求导
-
定义在元素是独立变量的p×qp×qp×q矩阵X∈RnX\in{\mathbb{R}^n}X∈Rn上的标量函数yyy对XXX的导数可以(用分子记法)写作
- ∂y∂X=[∂y∂x11∂y∂x21⋯∂y∂xp1∂y∂x12∂y∂x22⋯∂y∂xp2⋮⋮⋱⋮∂y∂x1q∂y∂x2q⋯∂y∂xpq]{\displaystyle {\frac {\partial y}{\partial \mathbf {X} }}={\begin{bmatrix}{\frac {\partial y}{\partial x_{11}}}&{\frac {\partial y}{\partial x_{21}}}&\cdots &{\frac {\partial y}{\partial x_{p1}}}\\{\frac {\partial y}{\partial x_{12}}}&{\frac {\partial y}{\partial x_{22}}}&\cdots &{\frac {\partial y}{\partial x_{p2}}}\\\vdots &\vdots &\ddots &\vdots \\{\frac {\partial y}{\partial x_{1q}}}&{\frac {\partial y}{\partial x_{2q}}}&\cdots &{\frac {\partial y}{\partial x_{pq}}}\\\end{bmatrix}}} ∂X∂y=∂x11∂y∂x12∂y⋮∂x1q∂y∂x21∂y∂x22∂y⋮∂x2q∂y⋯⋯⋱⋯∂xp1∂y∂xp2∂y⋮∂xpq∂y
-
定义矩阵上的重要的标量函数包括矩阵的迹和行列式
- y(X)=∣X∣y(X)=|X|y(X)=∣X∣
- y(X)=Tr(X)y(X)=Tr(X)y(X)=Tr(X)
-
类比于向量微积分,这个导数常被写成如下形式:
- ∇Xy(X)=∂y(X)∂X\displaystyle \nabla _{\mathbf {X} }y(\mathbf {X} )={\frac {\partial y(\mathbf {X} )}{\partial \mathbf {X} }} ∇Xy(X)=∂X∂y(X)
-
类似地,标量函数f(X)f(X)f(X)关于矩阵X在方向Y的方向导数可写成
- ∇Yf=tr(∂f∂XY)\displaystyle \nabla _{\mathbf {Y} }f=\operatorname {tr} \left({\frac {\partial f}{\partial \mathbf {X} }}\mathbf {Y} \right) ∇Yf=tr(∂X∂fY)
-
梯度矩阵经常被应用在估计理论的最小化问题中,比如卡尔曼滤波算法的推导,因此在这些领域中有着重要的地位。
相关文章:

ML@矩阵微积分基础
文章目录矩阵微积分Matrix calculus记法简单Jacobi Matrix分子记法分母记法一般形式的Jacobi MatrixTypes of matrix derivative向量求导向量对标量求导标量对向量求导向量对向量求导矩阵求导矩阵对标量求导(切矩阵)标量对矩阵求导记法向量求导 向量对标量求导标量对向量求导向…...
)
华为OD机试真题Python实现【优秀学员统计】真题+解题思路+代码(20222023)
优秀学员统计 题目 公司某部门软件教导团正在组织新员工每日打卡学习活动,他们开展这项学习活动已经一个月了,所以想统计下这个月优秀的打卡员工。每个员工会对应一个 id,每天的打卡记录记录当天打卡员工的 id 集合,一共 30 天。 请你实现代码帮助统计出打卡次数 top5 的…...

docsify在线文档支持pdf查看
目录 步骤一:添加插件 步骤二:添加pdf地址 步骤三:成果展示 docsify是一个在github上很好用的文档转换网页的工具,但是大部分情况我们都是使用的markdown文件。最近想把pdf文档也能支持在这上面展示,研究后总结一下…...

ES6中Set类型的基本使用
在ES6之前,存储数据的结构主要有两种:数组、对象。 在ES6中新增了另外两种数据结构(存放数据的方式):Set、Map,以及他们的另外形式WeakSet、WeakMap。 Set的基本使用 Set是一个新增的数据结构,…...
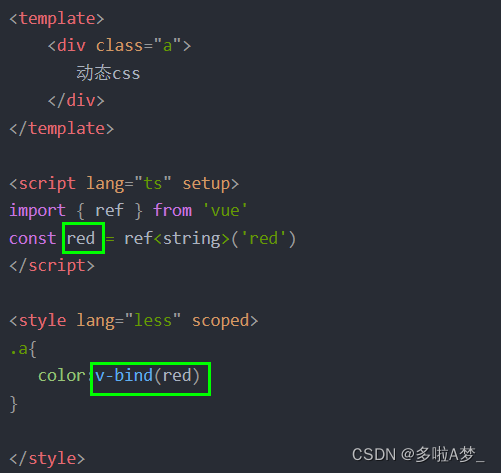
【VUE3.0_CSS功能】
CSS功能组件css作用域深度选择器(标签名空格:deep(标签名))插槽选择器(:soltted(标签名))全局选择器(:global(类名))动态CSS(v-bind)useCSSModule拓展知识:deep的写法组件…...

微机原理复习总结6:汇编语言程序设计
本篇博客主要分享几道汇编语言例题编写一完整的程序,从键盘输入一组字符,直到输入“0”为止,当输入是小写字母时,则修改为大写字母,输入的字符存放在string为首址的存储单元中。data segment ;数据段定义 st…...

计算机网络 部分原理和过程
下面是一台计算机 Ping 和不在同一 IP 网络上的另一台计算机的全过程: 该计算机首先确定要 Ping 的目标 IP 地址,并检查该 IP 地址是否与本地 IP 地址在同一 IP 网络上。如果目标 IP 地址与本地 IP 地址不在同一 IP 网络上,则需要通过路由器…...

C++实现链表
C实现链表 众所周知,C/C语言实现的链表是由一个一个的结点构成,每个结点分为数据域和指针域,指针域中存储了其后继结点的地址,通过地址来访问下一个结点。 链表是一系列节点串联形成的数据结构,链表存储有序的元素集合…...

MySQL索引篇
文章目录说明:索引篇一、索引常见面试题按数据结构按物理存储分类按字段特性分类按字段个数分类索引缺点:什么时候适用索引?什么时候不需要创建索引?常见优化索引的方法:发生索引失效的情况:二、从数据页角…...
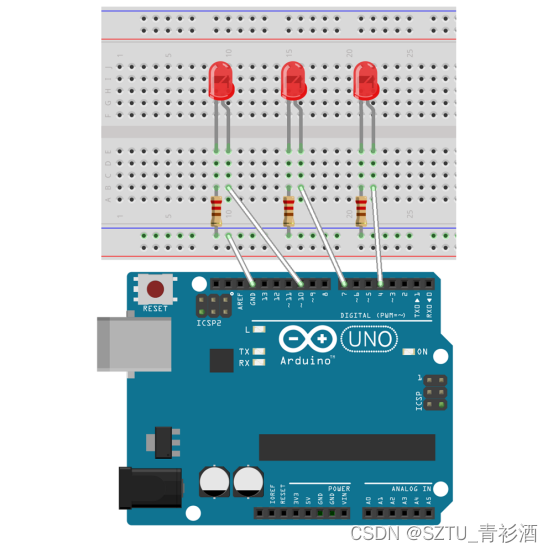
Ardiuno-交通灯
LED交通灯实验实验器件:■ 红色LED灯:1 个■ 黄色LED灯:1 个■ 绿色LED灯:1 个■ 220欧电阻:3 个■ 面包板:1 个■ 多彩杜邦线:若干实验连线1.将3个发光二极管插入面包板,2.用杜邦线…...

Leetcode.1234 替换子串得到平衡字符串
题目链接 Leetcode.1234 替换子串得到平衡字符串 Rating : 1878 题目描述 有一个只含有 Q, W, E, R四种字符,且长度为 n 的字符串。 假如在该字符串中,这四个字符都恰好出现 n/4次,那么它就是一个「平衡字符串」。 给你一个这样…...

聚类算法之K-means算法详解
文章目录 什么是聚类k-means算法简介牧师-村民模型算法步骤伪代码流程描述手动实现优缺点优点缺点算法调优与改进数据预处理合理选择 K 值手肘法Gap Statistic(间隔统计量)轮廓系数法(Silhouette Coefficient)Canopy算法拍脑袋法采用核函数K-means++ISODATA参考文献<...

电话呼入/呼出CSFB流程介绍
MO CSFB 注册的LAI跟SYS_INFO不同会触发LU流程;LU流程结束后,判断LOCATION UPDATING ACCEPT消息中的"Follow-on proceed"参数状态。(1)如果IE消息中有"Follow-on proceed",终端直接发送CM Service Request; (2)如果IE消息中没有"Follow-on procee…...

【比赛合集】9场可报名的「创新应用」、「程序设计」大奖赛,任君挑选!
CompHub 实时聚合多平台的数据类(Kaggle、天池…)和OJ类(Leetcode、牛客…)比赛。本账号同时会推送最新的比赛消息,欢迎关注!更多比赛信息见 CompHub主页 或 点击文末阅读原文以下信息仅供参考,以比赛官网为准目录创新应用赛&…...
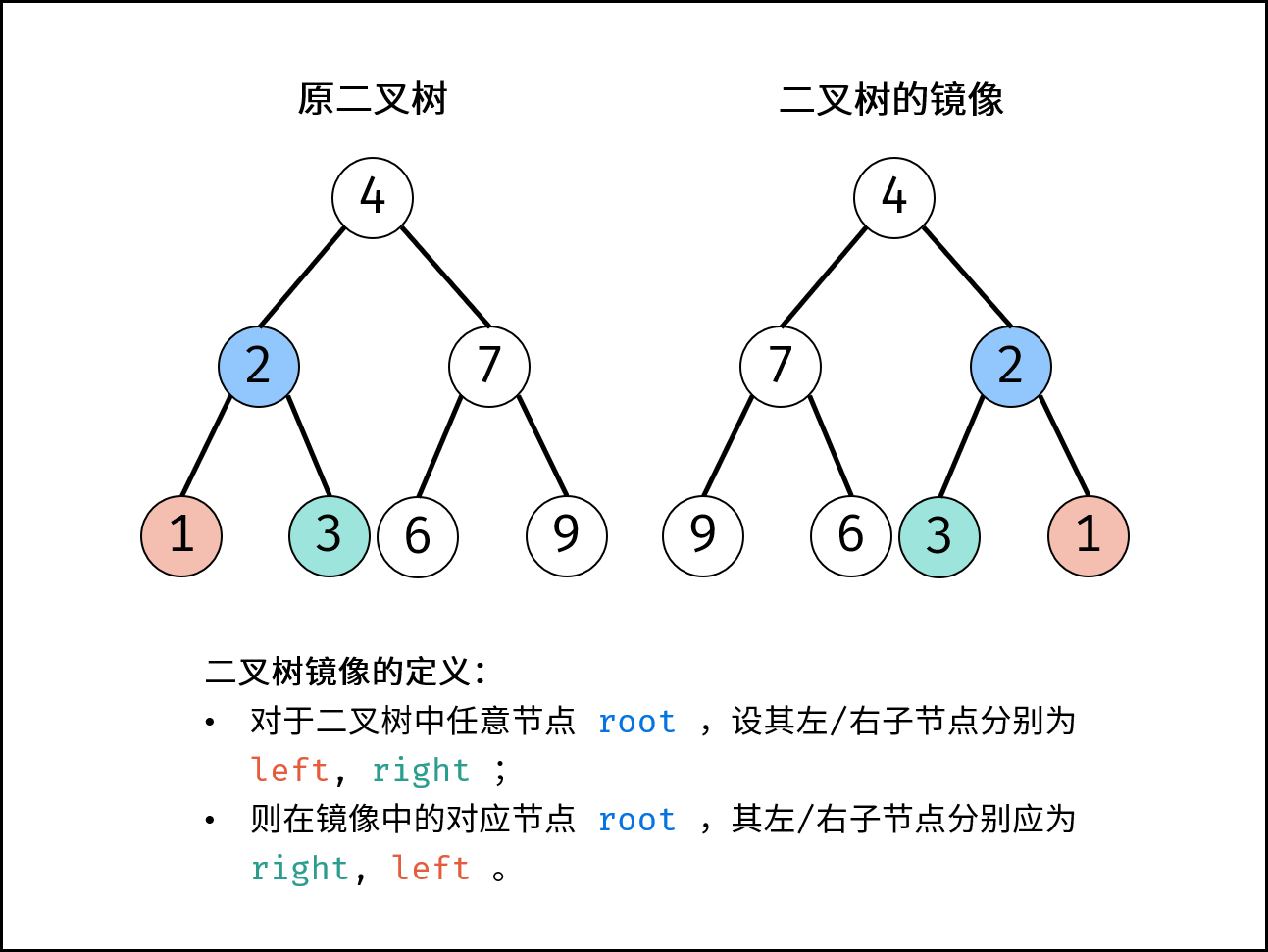
剑指 Offer 27. 二叉树的镜像
剑指 Offer 27. 二叉树的镜像 难度:easy\color{Green}{easy}easy 题目描述 请完成一个函数,输入一个二叉树,该函数输出它的镜像。 例如输入: 镜像输出: 示例 1: 输入:root [4,2,7,1,3,…...

RPC编程:RPC概述和架构演变
RPC编程系列文章第一篇一:引言1:本系列文章的目标2:RPC的概念二:架构的演变过程1:单体架构1):概念2):特点3):优缺点2:单体架构水平扩展1):水平拓展的含义2)&a…...

神经网络训练时只对指定的边更新参数
在神经网络中,通常采用反向传播算法来计算网络中各个参数的梯度,从而进行参数更新。在反向传播过程中,所有的参数都会被更新。因此,如果想要只更新指定的边,需要采用特殊的方法。 一种可能的方法是使用掩码࿰…...

Python列表list操作-遍历、查找、增加、删除、修改、排序
在使用列表的时候需要用到很多方法,例如遍历列表、查找元素、增加元素、删除元素、改变元素、插入元素、列表排序、逆序列表等操作。 1、遍历列表 遍历列表通常采用for循环的方式以及for循环和enumerate()函数搭配的方式去实现。 1ÿ…...

Python开发-学生管理系统
文章目录1、需求分析2、系统设计3、系统开发必备4、主函数设计5、 学生信息维护模块设计6、 查询/统计模块设计7、排序模块设计8、 项目打包1、需求分析 学生管理系统应具备的功能: ●添加学生及成绩信息 ●将学生信息保存到文件中 ●修改和删除学生信息 ●查询学生…...

大数据处理 - Trie树/数据库/倒排索引
Trie树Trie树的介绍和实现请参考 树 - 前缀树(Trie)适用范围: 数据量大,重复多,但是数据种类小可以放入内存基本原理及要点: 实现方式,节点孩子的表示方式扩展: 压缩实现。一些适用场景:寻找热门查询: 查询串的重复度比较高&#…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
