经典文献阅读之--VoxelMap(体素激光里程计)
0. 简介
作为激光里程计,常用的方法一般是特征点法或者体素法,最近Mars实验室发表了一篇文章《Efficient and Probabilistic Adaptive Voxel Mapping for Accurate Online LiDAR Odometry》,同时还开源了代码在Github上。文中为雷达里程计提出了一种高效的概率自适应体素建图方法。地图是体素的集合,每个体素包含一个平面(或边缘)特征能够实现对环境的概率表示和新的激光雷达帧的精确配准。我们进一步分析了对粗到细体素建图的需要,然后使用了新颖的使用哈希表组织体素地图和八叉树来有效地构建和更新地图。我们将所提出的体素建图应用于一个迭代扩展卡尔曼滤波器,并构造了一个姿态估计的最大后验概率问题。
1. 文章贡献
这篇文章作为一篇比较有影响力的文章,目前已经收到了国内比较多的关注,这里也是跟着Catalina大佬的博客,并结合自己阅读文章的理解进行介绍。
1.1 动机
- 直接用点云地图表达环境的方法很难考虑由雷达点云测量噪声带来的map的不确定性。地图的不确定性需要对点云中的特征进行显式参数化,在不同的 LiDAR 扫描帧中跟踪这些特征并估计这些特征参数及其不确定性比较困难。因为点云测量中的由于雷达分辨率、扫描类型以及空间点分布不均匀导致的,点密度随着扫描时间变化导致问题进一步变得复杂。此外,衡量map不确定性的时候还要考虑pose误差在系统中的传播。
- surfel方法通常建模很小的面特征,但场景中经常会有比较大的面特征。surfel的数据关联一般是将map中的surfel和测量帧surfel投影到一个图像上,这种渲染过程非常耗费时间。
- surfel建模为类似高斯混合模型的时候,一般通过EM算法来做数据关联,无效的surfel会和相邻的合并起来,进而自适应调节surfel尺寸,而自适应voxel的方法会更加鲁棒。
- ICP方法不够鲁棒,NDT方法不够精确,结合两者,先划分网格,在网格中估计平面参数,最终鲁棒性和精度都会比较好。
1.2 贡献
- 针对激光雷达点云的稀疏性和不规则性,提出了一种大小自适应、由粗到精的体素构建方法。自适应体素图被组织在八叉树-哈希表的数据结构中,以提高体素构建、更新和查询的效率。
2、本文提出了一种精确的概率体素地图表示法,准确地考虑了点测量和激光雷达位置估计引起的点不确定性,以对地图中平面的不确定性进行建模。
3、实现了所提出的系统在真实世界中的激光测距和测绘的应用,并与最新的方法进行了比较。
2. 详细内容
2.1 概率平面表达
这部分的主要内容是基于激光测量误差和位姿估计误差计算世界坐标系下点的误差,基于平面法向量估计方式估计法向量的误差。
2.1.1 原始点测量噪声
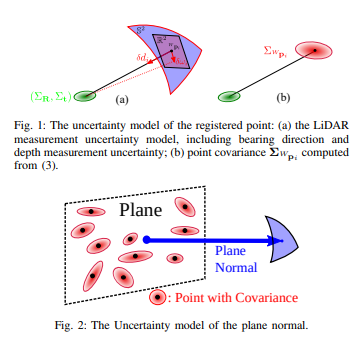
点云噪声来源于2部分,一是range测距不确定性(depth),二是bearing direction方位不确定性(w),公式可从我们的之前工作《Pixel-level Extrinsic Self Calibration of High Resolution LiDAR and Camera in Targetless Environments》推导得到。高斯建模如下
δωi∼N(02×1,Σωi),δdi∼N(0,Σdi)\boldsymbol{\delta}_{\boldsymbol{\omega}_i} \sim \mathcal{N}\left(\mathbf{0}_{2 \times 1}, \boldsymbol{\Sigma}_{\boldsymbol{\omega}_i}\right), \delta_{d_i} \sim \mathcal{N}\left(0, \Sigma_{d_i}\right)δωi∼N(02×1,Σωi),δdi∼N(0,Σdi)
设ωi∈S2ω_i∈\mathbb{S}^2ωi∈S2为测量的轴承方向,δωi∼N(02×1,Σωi)δ_{ω_i} \sim \mathcal{N} (0_{2×1}, Σ_{ω_i})δωi∼N(02×1,Σωi)为ωiω_iωi切平面上的轴承方向噪声,did_idi为深度测量值,δdiN(0,Σdi)δ_{d_i} ~ N (0, Σ_{d_i})δdi N(0,Σdi)为测距噪声。得到测量点Lpi^Lp_iLpi及其协方差ΣLpiΣ_{L_{p_i}}ΣLpi的噪声δLpiδ_{L_{p_i}}δLpi
δLpi=[ωi−di⌊ωi⌋∧N(ωi)]⏟Ai[δdiδωi]∼N(0,ΣLpi)ΣLpi=Ai[Σdi01×202×1Σωi]AiT\boldsymbol{\delta}_{L_{\mathbf{p}_i}}=\underbrace{\left[\begin{array}{ll}\boldsymbol{\omega}_i & -d_i\left\lfloor\boldsymbol{\omega}_i\right\rfloor \wedge \mathbf{N}\left(\boldsymbol{\omega}_i\right)\end{array}\right]}_{\mathbf{A}_i}\left[\begin{array}{c}\delta_{d_i} \\ \boldsymbol{\delta}_{\boldsymbol{\omega}_i}\end{array}\right] \sim \mathcal{N}\left(\mathbf{0}, \boldsymbol{\Sigma}_{L_{\mathbf{p}_i}}\right) \\ \boldsymbol{\Sigma}_{L_{\mathbf{p}_i}}=\mathbf{A}_i\left[\begin{array}{cc} \Sigma_{d_i} & \mathbf{0}_{1 \times 2} \\ \mathbf{0}_{2 \times 1} & \boldsymbol{\Sigma}_{\boldsymbol{\omega}_i} \end{array}\right] \mathbf{A}_i^TδLpi=Ai[ωi−di⌊ωi⌋∧N(ωi)][δdiδωi]∼N(0,ΣLpi)ΣLpi=Ai[Σdi02×101×2Σωi]AiT
其中N(ωi)=[N1N2]∈R3×2N(ω_i) = [N_1 N_2]∈\mathbb{R}^{3×2}N(ωi)=[N1N2]∈R3×2是ωi处切平面的标准正交基,⌊⌋∧\lfloor \rfloor_∧⌊⌋∧为映射叉积的斜对称矩阵。式(1)的详细推导可以在[27]中找到。
world系下点的坐标及其不确定性为下面的公式。ΣRΣ_RΣR是LWR^W_LRLWR在切平面空间的不确定性,ΣtΣ_tΣt是下式中ttt的不确定性。
Wpi=LWRLpi+LWtΣWpi=LWRΣLpiLWRT+LWR⌊Lpi⌋∧ΣRLpi⌋∧LTWRT+Σt{ }^W \mathbf{p}_i={ }_L^W \mathbf{R}^L \mathbf{p}_i+{ }_L^W \mathbf{t}\\ \left.\boldsymbol{\Sigma}_{W_{\mathbf{p}_i}}={ }_L^W \mathbf{R} \boldsymbol{\Sigma}_{L_{\mathbf{p}_i L}}{ }^W \mathbf{R}^T+{ }_L^W \mathbf{R}\left\lfloor{ }^L \mathbf{p}_i\right\rfloor_{\wedge} \boldsymbol{\Sigma}_{\mathbf{R}}{ }^L \mathbf{p}_i\right\rfloor_{\wedge L}^{T W} \mathbf{R}^T+\boldsymbol{\Sigma}_{\mathbf{t}}Wpi=LWRLpi+LWtΣWpi=LWRΣLpiLWRT+LWR⌊Lpi⌋∧ΣRLpi⌋∧LTWRT+Σt
2.1.2 平面的不确定性
设一个平面特征由一组LiDAR点Wpi(i=1,…,N)^Wp_i (i = 1,…, N)Wpi(i=1,…,N),由于测量噪声和位姿估计误差,每个点都有一个不确定性WΣpi^WΣ_{p_i}WΣpi,如(3)所示。表示点的协方差矩阵为AAA:
p‾=1N∑i=1NWpi;A=1N∑i=1N(Wpi−p‾)(Wpi−p‾)T\overline{\mathbf{p}}=\frac{1}{N} \sum_{i=1}^N{ }^W \mathbf{p}_i ; \quad \mathbf{A}=\frac{1}{N} \sum_{i=1}^N\left({ }^W \mathbf{p}_i-\overline{\mathbf{p}}\right)\left({ }^W \mathbf{p}_i-\overline{\mathbf{p}}\right)^T p=N1i=1∑NWpi;A=N1i=1∑N(Wpi−p)(Wpi−p)T
然后,平面可以表示为它的法向量nnn,它是与AAA的最小特征值相关联的特征向量,点q=pˉq = \bar{p}q=pˉ,它位于这个平面上。由于AAA和ppp都依赖于Wpi^Wp_iWpi,我们可以将平面参数(n,q)(n, q)(n,q)表示为Wpi^Wp_iWpi的函数,如下所示:
[n,q]T=f(Wp1,Wp2,…,WpN)[\mathbf{n}, \mathbf{q}]^T=\mathbf{f}\left({ }^W \mathbf{p}_1,{ }^W \mathbf{p}_2, \ldots,{ }^W \mathbf{p}_N\right)[n,q]T=f(Wp1,Wp2,…,WpN)
那么真实世界中的平面normal和位置点q可以估计为下面公式
[ngt,qgt]T=f(Wp1+δWp1,Wp2+δWp1,…,WpN+δWpN)≈[n,q]T+∑i=1N∂f∂WpiδWpi\begin{aligned} {\left[\mathbf{n}^{g t}, \mathbf{q}^{g t}\right]^T } &=\mathbf{f}\left({ }^W \mathbf{p}_1+\boldsymbol{\delta}_{W_{\mathbf{p}_1}},{ }^W \mathbf{p}_2+\boldsymbol{\delta}_{W_{\mathbf{p}_1}}, \ldots,{ }^W \mathbf{p}_N+\boldsymbol{\delta}_{W_{\mathbf{p}_N}}\right) \\ & \approx[\mathbf{n}, \mathbf{q}]T+\sum_{i=1}N \frac{\partial \mathbf{f}}{\partial{ }^W \mathbf{p}_i} \boldsymbol{\delta}_{W_{\mathbf{p}_i}} \end{aligned}[ngt,qgt]T=f(Wp1+δWp1,Wp2+δWp1,…,WpN+δWpN)≈[n,q]T+i=1∑N∂Wpi∂fδWpi
∂f∂Wpi=[∂n∂Wpi,∂q∂Wpi]T\frac{\partial \mathbf{f}}{\partial^W \mathbf{p}_i}=\left[\frac{\partial \mathbf{n}}{\partial^W \mathbf{p}_i}, \frac{\partial \mathbf{q}}{\partial{ }^W \mathbf{p}_i}\right]^T∂Wpi∂f=[∂Wpi∂n,∂Wpi∂q]T
假设AAA有特征向量矩阵UUU、最小特征值λ3λ_3λ3和对应的特征向量u3u_3u3,参照[28],我们可以对每个点Wpi^Wp_iWpi取nnn和qqq的导数,如下所示:
∂n∂Wpi=U[F1,3piF2,3piF3,3pi],Fm,3pi={(Wpi−q)TN(λ3−λm)(umnT+numT),m≠301×3,m=3∂q∂Wpi=diag(1N,1N,1N)\begin{aligned} &\frac{\partial \mathbf{n}}{\partial W_{\mathbf{p}_i}}=\mathbf{U}\left[\begin{array}{l} \mathbf{F}_{1,3}^{\mathbf{p}_i} \\ \mathbf{F}_{2,3}^{\mathbf{p}_i} \\ \mathbf{F}_{3,3}^{\mathbf{p}_i} \end{array}\right], \mathbf{F}_{m, 3}^{\mathbf{p}_i}=\left\{\begin{array}{cc} \frac{\left({ }{\left.W_{\mathbf{p}_i}-\mathbf{q}\right)T}\right.}{N\left(\lambda_3-\lambda_m\right)}\left(\mathbf{u}_m \mathbf{n}^T+\mathbf{n u}_m^T\right) & , m \neq 3 \\ \mathbf{0}_{1 \times 3} & , m=3 \end{array}\right.\\ &\frac{\partial \mathbf{q}}{\partial W_{\mathbf{p}_i}}=\operatorname{diag}\left(\frac{1}{N}, \frac{1}{N}, \frac{1}{N}\right) \end{aligned}∂Wpi∂n=UF1,3piF2,3piF3,3pi,Fm,3pi={N(λ3−λm)(Wpi−q)T(umnT+numT)01×3,m=3,m=3∂Wpi∂q=diag(N1,N1,N1)
Σn,q=∑i=1N∂f∂WpiΣWpi∂f∂Wpi\boldsymbol{\Sigma}_{\mathbf{n}, \mathbf{q}}=\sum_{i=1}^N \frac{\partial \mathbf{f}}{\partial{ }^W \mathbf{p}_i} \boldsymbol{\Sigma}_{W_{\mathbf{p}_i}} \frac{\partial \mathbf{f}}{\partial{ }^W \mathbf{p}_i}Σn,q=i=1∑N∂Wpi∂fΣWpi∂Wpi∂f

2.2 由粗到细的体素地图构建方法
地图由哈希表和八叉树构成,哈希表管理最上层的地图结构,八叉树每个节点中存放一个平面,如果一个节点中的点不能被表示为一个特征,拆分这个节点。
后续地图的点被送到对应的节点中,在面特征稳定后删除旧的观测,只保留最新观测,如果新的观测和旧的观测冲突,删去旧估计重写估计位姿。
- Motivation
激光雷达点通常是按顺序采样的,因此点云的扫描总是从稀疏到密集,特别是在点分布的室外环境中更大的空间。当点云相对稀疏时,常用的基于面元的方法通常只能获得非常少量的平面,限制了高精确的和相对较低的扫描率的激光雷达的使用(例如,10Hz),这样就可以积累足够数量的点。然而,这将需要在累积的范围内补偿运动。为了解决这个问题,我们提出了一种从粗到细的体素建图方法,该方法可以在点云稀疏时构建一个粗糙的体素地图,并在接收到更多的点时对地图进行细化。
- Voxel Map Construction

- Map Update
对于在线激光雷达里程计,新的激光雷达点云帧不断的进入并且配准,并估计了它们的姿态。然后使用估计的姿态将新点注册到全局地图中:当新点位于一个未填充的体素中时,它将构造该体素。否则,当将新点添加到现有体素时,应该更新体素中平面的参数和不确定性。
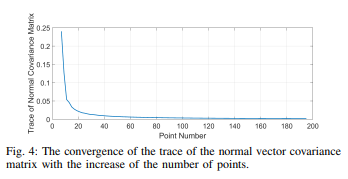
上图展示了不确定度的快速收敛。其中每个点的位置携带一个均值为零和方差0.1的高斯噪声。在不确定性收敛后,我们丢弃所有的历史点,并保留估计的平面参数(n,q)和协方差Σ,q。一旦新的累计点出现,我们只保留最新的10点,并计算出由这10个点组成的新平面法向量。如果新的法向量和先前收敛的法向量继续出现相对较大的差值,我们认为地图的这个区域已经发生了变化,需要重新使用算法1计算。
2.3 点与平面匹配
基于对点和平面的精确不确定性建模,我们可以很容易地实现点对平面的匹配。给定一个在具有姿态先验的世界框架中预测的激光雷达点WPi^WP_iWPi,我们首先通过它的哈希键找到它所在的根体素(具有粗糙的地图分辨率)。然后,对所有包含的子体素进行轮询,以此与点匹配。具体来说,让一个子体素包含一个具有法线nin_ini和中心qiq_iqi的平面,我们计算了点-平面距离:
di=niT(Wpi−qi)d_i=\mathbf{n}_i^T\left({ }^W \mathbf{p}_i-\mathbf{q}_i\right)di=niT(Wpi−qi)
考虑到所有这些不确定性:
di=(nigt⊞δni)T[(Wpigt+δWpi)−qigt−δqi]≈nigtT(Wpigt−qigt)⏟0+Jniδni+Jqiδqi+JWpiδWpi⏟wi\begin{aligned} &d_i=\left(\mathbf{n}_i^{g t} \boxplus \boldsymbol{\delta}_{\mathbf{n}_i}\right)^T\left[\left({ }^W \mathbf{p}_i^{g t}+\boldsymbol{\delta}_{W_{\mathbf{p}_i}}\right)-\mathbf{q}_i^{g t}-\boldsymbol{\delta}_{\mathbf{q}_i}\right]\\ &\approx \underbrace{\mathbf{n}_i^{g t T}\left({ }^W \mathbf{p}_i^{g t}-\mathbf{q}_i^{g t}\right)}_0+\underbrace{\mathbf{J}_{\mathbf{n}_i} \boldsymbol{\delta}_{\mathbf{n}_i}+\mathbf{J}_{\mathbf{q}_i} \boldsymbol{\delta}_{\mathbf{q}_i}+\mathbf{J}_{W_{\mathbf{p}_i}} \boldsymbol{\delta}_{W_{\mathbf{p}_i}}}_{\mathbf{w}_i} \end{aligned}di=(nigt⊞δni)T[(Wpigt+δWpi)−qigt−δqi]≈0nigtT(Wpigt−qigt)+wiJniδni+Jqiδqi+JWpiδWpi
也就是说,如果该点位于候选平面上,其距离did_idi应服从(10)中的分布。因此,假设分布的标准差为σ=Σwiσ = \sqrt{^Σw_i}σ=Σwi,就可以检验点面距离是否在3σ3σ3σ内。如果是,则选择为有效匹配。此外,如果一个点基于3σ3σ3σ准则匹配多个平面,则匹配概率最大的平面。如果没有平面通过3σ3σ3σ检验,则丢弃该点,以消除由体素量化引起的可能的错误匹配。
2.4 状态估计(基于卡尔曼滤波的定位方法)
我们建立了一个基于类似于FAST-LIO2的迭代扩展卡尔曼滤波器的激光雷达里程计,与C节中匹配的点到点平面距离进行融合,形成最大后验(MAP)估计。具体地说,第i个有效的点到平面匹配得到观测方程:
zi=hi(xk)+viz_i = h_i(x_k) + v_izi=hi(xk)+vi
线性化可以得到

…详情请参照古月居
相关文章:

经典文献阅读之--VoxelMap(体素激光里程计)
0. 简介 作为激光里程计,常用的方法一般是特征点法或者体素法,最近Mars实验室发表了一篇文章《Efficient and Probabilistic Adaptive Voxel Mapping for Accurate Online LiDAR Odometry》,同时还开源了代码在Github上。文中为雷达里程计提…...
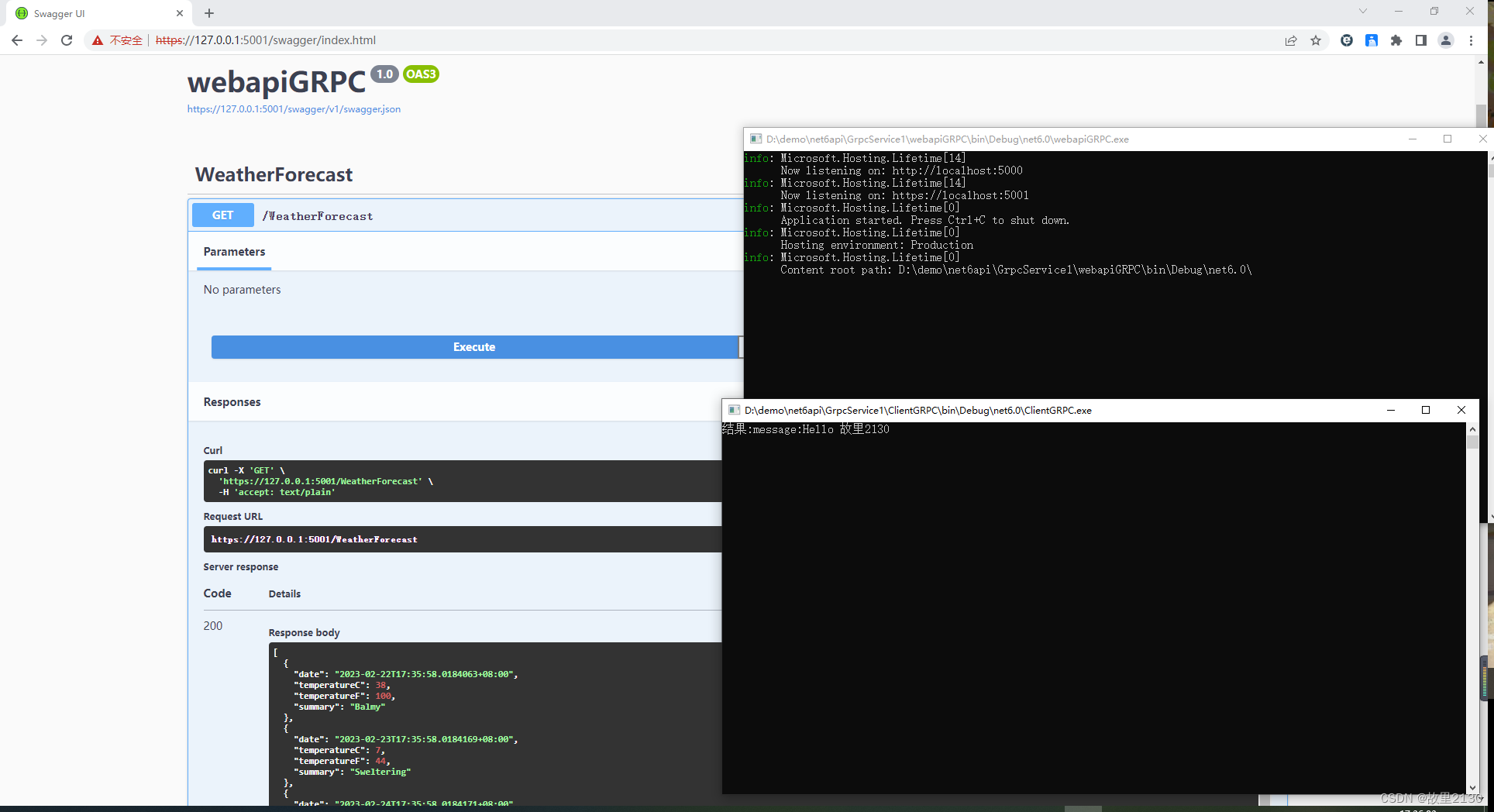
.NET6中使用GRPC详细描述
Supported languages | gRPC,官网。至于原理就不说了,可以百度原理之后,然后再结合代码,事半功倍,就能很好理解GRPC了。 目录 一、简单使用 二、实际应用 一、简单使用 1.使用vs2022创建一个grpc程序,…...

ML@矩阵微积分基础
文章目录矩阵微积分Matrix calculus记法简单Jacobi Matrix分子记法分母记法一般形式的Jacobi MatrixTypes of matrix derivative向量求导向量对标量求导标量对向量求导向量对向量求导矩阵求导矩阵对标量求导(切矩阵)标量对矩阵求导记法向量求导 向量对标量求导标量对向量求导向…...
)
华为OD机试真题Python实现【优秀学员统计】真题+解题思路+代码(20222023)
优秀学员统计 题目 公司某部门软件教导团正在组织新员工每日打卡学习活动,他们开展这项学习活动已经一个月了,所以想统计下这个月优秀的打卡员工。每个员工会对应一个 id,每天的打卡记录记录当天打卡员工的 id 集合,一共 30 天。 请你实现代码帮助统计出打卡次数 top5 的…...

docsify在线文档支持pdf查看
目录 步骤一:添加插件 步骤二:添加pdf地址 步骤三:成果展示 docsify是一个在github上很好用的文档转换网页的工具,但是大部分情况我们都是使用的markdown文件。最近想把pdf文档也能支持在这上面展示,研究后总结一下…...

ES6中Set类型的基本使用
在ES6之前,存储数据的结构主要有两种:数组、对象。 在ES6中新增了另外两种数据结构(存放数据的方式):Set、Map,以及他们的另外形式WeakSet、WeakMap。 Set的基本使用 Set是一个新增的数据结构,…...
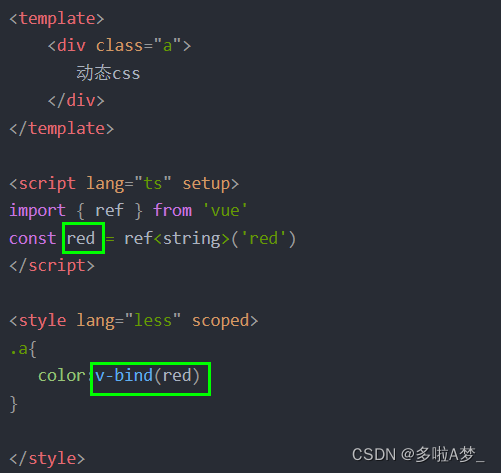
【VUE3.0_CSS功能】
CSS功能组件css作用域深度选择器(标签名空格:deep(标签名))插槽选择器(:soltted(标签名))全局选择器(:global(类名))动态CSS(v-bind)useCSSModule拓展知识:deep的写法组件…...

微机原理复习总结6:汇编语言程序设计
本篇博客主要分享几道汇编语言例题编写一完整的程序,从键盘输入一组字符,直到输入“0”为止,当输入是小写字母时,则修改为大写字母,输入的字符存放在string为首址的存储单元中。data segment ;数据段定义 st…...

计算机网络 部分原理和过程
下面是一台计算机 Ping 和不在同一 IP 网络上的另一台计算机的全过程: 该计算机首先确定要 Ping 的目标 IP 地址,并检查该 IP 地址是否与本地 IP 地址在同一 IP 网络上。如果目标 IP 地址与本地 IP 地址不在同一 IP 网络上,则需要通过路由器…...

C++实现链表
C实现链表 众所周知,C/C语言实现的链表是由一个一个的结点构成,每个结点分为数据域和指针域,指针域中存储了其后继结点的地址,通过地址来访问下一个结点。 链表是一系列节点串联形成的数据结构,链表存储有序的元素集合…...

MySQL索引篇
文章目录说明:索引篇一、索引常见面试题按数据结构按物理存储分类按字段特性分类按字段个数分类索引缺点:什么时候适用索引?什么时候不需要创建索引?常见优化索引的方法:发生索引失效的情况:二、从数据页角…...
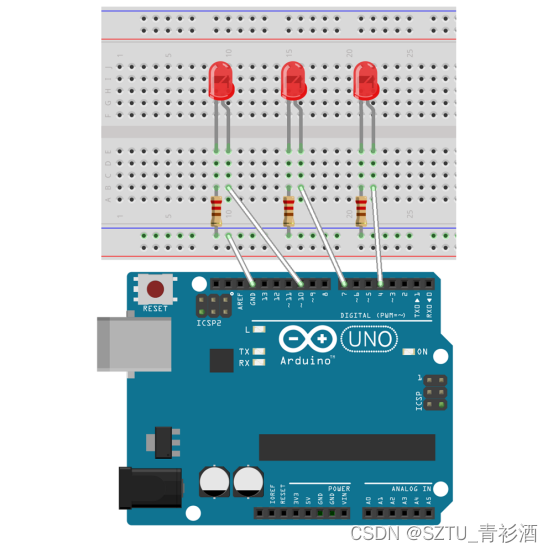
Ardiuno-交通灯
LED交通灯实验实验器件:■ 红色LED灯:1 个■ 黄色LED灯:1 个■ 绿色LED灯:1 个■ 220欧电阻:3 个■ 面包板:1 个■ 多彩杜邦线:若干实验连线1.将3个发光二极管插入面包板,2.用杜邦线…...

Leetcode.1234 替换子串得到平衡字符串
题目链接 Leetcode.1234 替换子串得到平衡字符串 Rating : 1878 题目描述 有一个只含有 Q, W, E, R四种字符,且长度为 n 的字符串。 假如在该字符串中,这四个字符都恰好出现 n/4次,那么它就是一个「平衡字符串」。 给你一个这样…...

聚类算法之K-means算法详解
文章目录 什么是聚类k-means算法简介牧师-村民模型算法步骤伪代码流程描述手动实现优缺点优点缺点算法调优与改进数据预处理合理选择 K 值手肘法Gap Statistic(间隔统计量)轮廓系数法(Silhouette Coefficient)Canopy算法拍脑袋法采用核函数K-means++ISODATA参考文献<...

电话呼入/呼出CSFB流程介绍
MO CSFB 注册的LAI跟SYS_INFO不同会触发LU流程;LU流程结束后,判断LOCATION UPDATING ACCEPT消息中的"Follow-on proceed"参数状态。(1)如果IE消息中有"Follow-on proceed",终端直接发送CM Service Request; (2)如果IE消息中没有"Follow-on procee…...

【比赛合集】9场可报名的「创新应用」、「程序设计」大奖赛,任君挑选!
CompHub 实时聚合多平台的数据类(Kaggle、天池…)和OJ类(Leetcode、牛客…)比赛。本账号同时会推送最新的比赛消息,欢迎关注!更多比赛信息见 CompHub主页 或 点击文末阅读原文以下信息仅供参考,以比赛官网为准目录创新应用赛&…...
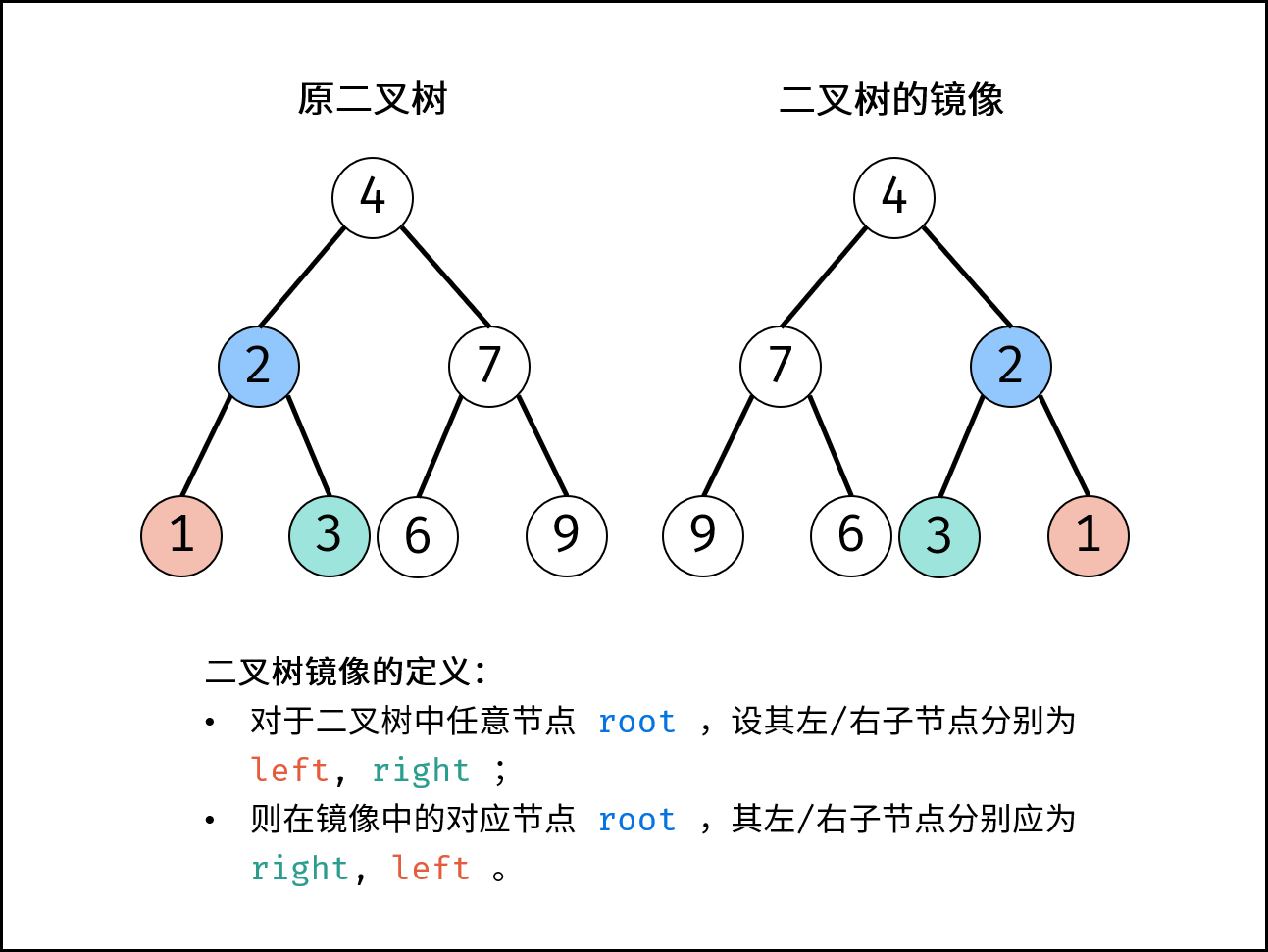
剑指 Offer 27. 二叉树的镜像
剑指 Offer 27. 二叉树的镜像 难度:easy\color{Green}{easy}easy 题目描述 请完成一个函数,输入一个二叉树,该函数输出它的镜像。 例如输入: 镜像输出: 示例 1: 输入:root [4,2,7,1,3,…...

RPC编程:RPC概述和架构演变
RPC编程系列文章第一篇一:引言1:本系列文章的目标2:RPC的概念二:架构的演变过程1:单体架构1):概念2):特点3):优缺点2:单体架构水平扩展1):水平拓展的含义2)&a…...

神经网络训练时只对指定的边更新参数
在神经网络中,通常采用反向传播算法来计算网络中各个参数的梯度,从而进行参数更新。在反向传播过程中,所有的参数都会被更新。因此,如果想要只更新指定的边,需要采用特殊的方法。 一种可能的方法是使用掩码࿰…...

Python列表list操作-遍历、查找、增加、删除、修改、排序
在使用列表的时候需要用到很多方法,例如遍历列表、查找元素、增加元素、删除元素、改变元素、插入元素、列表排序、逆序列表等操作。 1、遍历列表 遍历列表通常采用for循环的方式以及for循环和enumerate()函数搭配的方式去实现。 1ÿ…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
