mkp勒索病毒的介绍和防范,勒索病毒解密,数据恢复
mkp勒索病毒是一种新兴的电脑病毒,它会对感染的电脑进行加密,并要求用户支付一定的赎金才能解锁。这种病毒已经引起了全球范围内的关注,因为它不仅具有高危害性,而且还有很强的传播能力。本文将对mkp勒索病毒进行详细介绍,分析其特点和危害,并提出防范措施。

一、mkp勒索病毒的简介
mkp勒索病毒是一种新兴的电脑病毒,它主要通过电子邮件、网络下载、文件共享等途径进行传播。一旦感染了这种病毒,电脑中的文件就会被加密,并要求用户支付一定的赎金才能解锁。这种病毒的名称来源于其加密算法的名称——Matrix Kryptonite,也称为“MKP”。
二、mkp勒索病毒的特点
- 高危害性:mkp勒索病毒可以对电脑中的所有文件进行加密,包括文档、照片、视频等。一旦感染了这种病毒,用户必须支付一定的赎金才能解锁文件,否则将无法正常使用电脑。
- 强大的传播能力:mkp勒索病毒可以通过电子邮件、网络下载、文件共享等途径进行传播。一旦被打开或下载,它就可以在短时间内感染整个网络。
- 难以防范:mkp勒索病毒的传播途径多种多样,很难通过单一的防范措施来防止其传播。此外,该病毒的加密算法非常强大,很难通过技术手段破解。
三、mkp勒索病毒的危害
- 影响工作和生活:mkp勒索病毒会对电脑中的所有文件进行加密,包括文档、照片、视频等。这将对用户的工作和生活造成极大的影响。
- 威胁个人信息:mkp勒索病毒要求用户支付一定的赎金才能解锁文件。如果用户被迫支付赎金,这将使个人信息暴露于风险之中。
- 影响社会稳定:mkp勒索病毒的传播速度快,影响范围广,如果大规模爆发,将对社会稳定造成一定的影响。
四、防范措施
- 加强个人电脑的安全防护:及时更新操作系统和软件补丁,安装杀毒软件和防火墙,不随意打开未知来源的邮件和文件等。
- 强化网络安全意识:不随意下载和打开未知来源的文件,不轻易点击电子邮件中的链接和附件,不随意访问不安全的网站等。
- 备份重要数据:定期备份重要数据,以防止病毒加密后无法恢复数据的情况发生。
- 提高网络安全意识:加强网络安全教育,提高公众对网络安全的认识和意识。
总之,mkp勒索病毒是一种高危害性的电脑病毒,它不仅会对个人造成极大的影响,还会对社会稳定造成一定的影响。因此,我们必须加强个人电脑的安全防护,强化网络安全意识,提高网络安全意识,共同维护网络安全。
相关文章:

mkp勒索病毒的介绍和防范,勒索病毒解密,数据恢复
mkp勒索病毒是一种新兴的电脑病毒,它会对感染的电脑进行加密,并要求用户支付一定的赎金才能解锁。这种病毒已经引起了全球范围内的关注,因为它不仅具有高危害性,而且还有很强的传播能力。本文将对mkp勒索病毒进行详细介绍…...

【面试精品】关于面试会遇到的Apache相关的面试题
1. Apache HTTP Server 基于什么协议提供网页浏览服务? 答:基于标准的http网络协议提供网页浏览服务。 2. 简述编译安装httpd软件包的基本过程? 答:解包,配置,编译,安装。 3. 编译安装httpd软…...

python对文件转md5,用于文件重复过滤
直接上代码 import hashlibdef calculate_md5(file_path):# 创建 MD5 哈希对象md5_hash hashlib.md5()# 打开文件并逐块读取,更新哈希值with open(file_path, rb) as file:while True:data file.read(8192) # 逐块读取文件,每块大小为 8192 字节if n…...

mac苹果电脑删除顽固残留软件图标
核心:删除“启动台”数据库里对应app的信息 1、打开访达(Finder),点击最顶部菜单栏的【前往》前往文件夹】,接着输入【/private/var/folders】 2、在弹出的访达(Finder)窗口搜索栏输入【com.ap…...

【jsvue】联合gtp仿写一个简单的vue框架,以此深度学习JavaScript
用 gtp 学习 Vue 生命周期的原理 lifecycle.js function Vue(options) {// 将选项保存到实例的 $options 属性中this.$options options;// 若存在 beforeCreate 钩子函数,则调用之if (typeof options.beforeCreate function) {options.beforeCreate.call(this);…...

linux centos7 系统之编程:求水仙花数
在Python编程中,有列表、元组和字典三类变量可以使用,方便数据的存储与处理,而bash中仅有字符串变量、数组、函数可用,方法运用上受到限制,这与bash基于C语言,注重语法结构的严谨有关。而Python等高级语言更…...

git中的cherry-pick和merge有些区别以及cherry-pick怎么用
git中的cherry-pick和merge在使用场景上有些区别: cherry-pick用于将另一个分支的某一次或几次commit应用到当前分支。它可以选择性地拉取代码修改。merge用于将两个分支合并成一个新分支。它会把整个分支上的所有修改都合并过来。 具体区别:cherry-pick通常用于将bug修复从发…...
【前端】CSS-Flex弹性盒模型布局
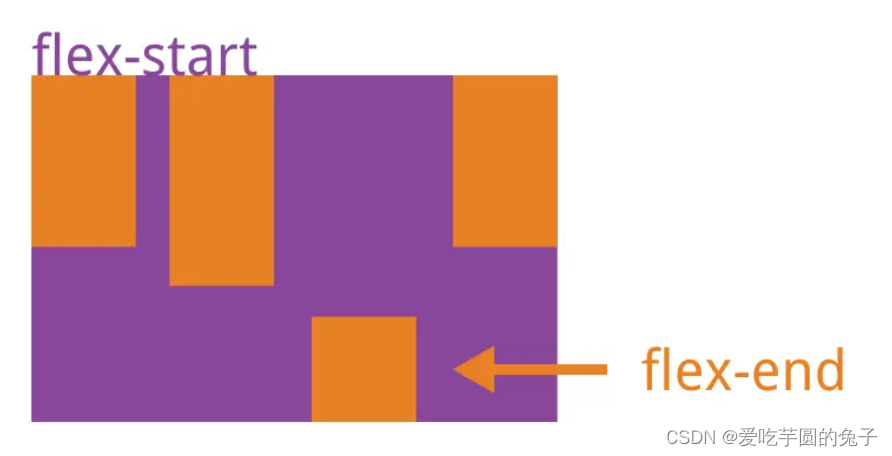
目录 一、前言二、Flex布局是什么1、任何一个容器都可以指定为Flex布局2、行内元素也可以使用Flex布局3、Webkit内核的浏览器,必须加上-webkit前缀 三、基本概念四、flex常用的两种属性1、容器属性2、项目属性 五、容器属性1、flex-direction①、定义②、语句1&…...

Android AAPT: error: resource color 异常原因处理
异常体现: Android resource linking failed ERROR:E:\software\Developer\APP\GaoDeTest2\app\src\main\res\values\themes.xml:3:5-9:13: AAPT: error: resource color/purple_500 (aka com.example.gaodetest2:color/purple_500) not found.ERROR:E:\software\De…...
的概念)
C++std::function和std::bind()的概念
std::function: 一个通用的函数封装器,它允许你存储和调用任何可以被调用的东西,例如函数、函数指针、函数对象、Lambda 表达式等。 std::bind: 用于创建函数对象。一个可调用对象的绑定版本,可以提前绑定某些参数&am…...

QT Creator工具介绍及使用
一、QT的基本概念 QT主要用于图形化界面的开发, QT是基于C编写的一套界面相关的类库,如进程线程库,网络编程的库,数据库操作的库,文件操作的库等。 如何使用这个类库:类库实例化对象(构造函数) --> 学习…...

python爬虫13:pymysql库
python爬虫13:pymysql库 前言 python实现网络爬虫非常简单,只需要掌握一定的基础知识和一定的库使用技巧即可。本系列目标旨在梳理相关知识点,方便以后复习。 申明 本系列所涉及的代码仅用于个人研究与讨论,并不会对网站产生…...

权限管理 ACL、RBAC、ABAC的学习
ACL(Access Control List:访问控制列表) 最简单的一种方式,将权限直接与用户或用户组相关联,管理员直接给用户授予某些权限即可。 这种模型适用于小型和简单系统,权限一块较为简单,并且角色和权限的变化较少。 RBAC(R…...

python的re正则表达式
一、正在表达式的方法(): re是Python中用于处理正则表达式的内置库,提供了许多有用的方法。以下是其中几个常用的方法: re.match(pattern, string): 尝试从字符串的开头匹配一个模式,如果匹配成功则返回匹…...

【算法与数据结构】700、LeetCode二叉搜索树中的搜索
文章目录 一、题目二、解法三、完整代码 所有的LeetCode题解索引,可以看这篇文章——【算法和数据结构】LeetCode题解。 一、题目 二、解法 思路分析:二叉搜索树的性质:左节点键值 < 中间节点键值 < 右节点键值。那么我们根据此性质&am…...
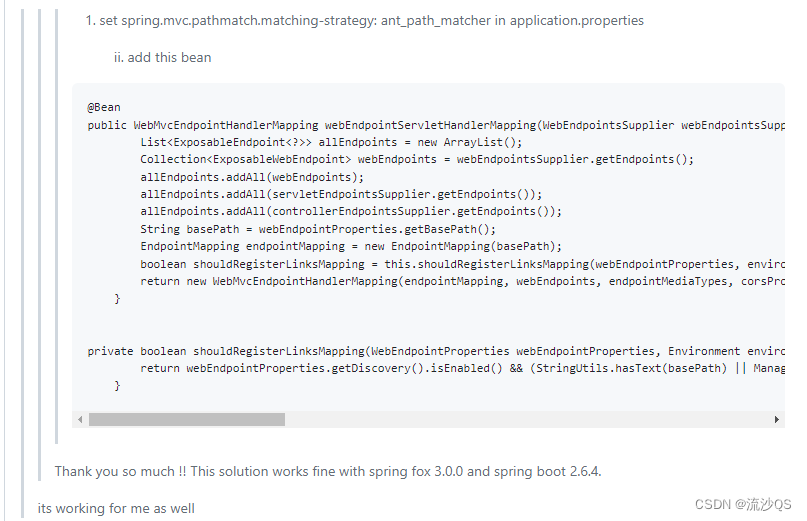
SpringBoot v2.7.x+ 整合Swagger3入坑记?
目录 一、依赖 二、集成Swagger Java Config 三、配置完毕 四、解决方案 彩蛋 想尝鲜,坑也多,一起入个坑~ 一、依赖 SpringBoot版本:2.7.14 Swagger版本:3.0.0 <dependency><groupId>com.github.xiaoymin<…...
说说你了解的 CDC
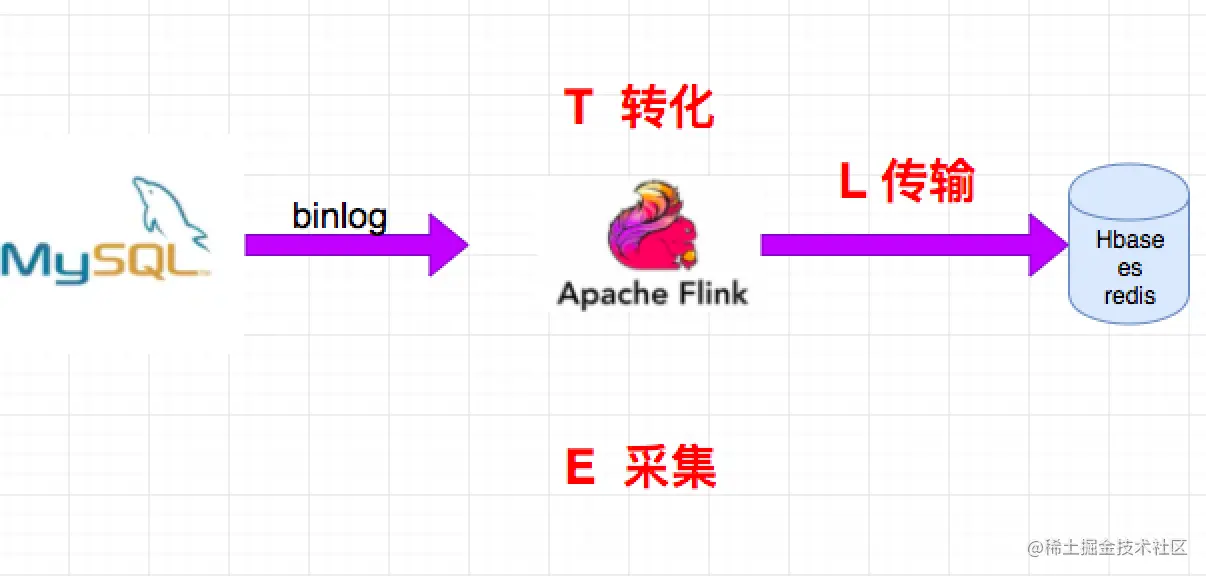
分析&回答 什么是 CDC CDC,Change Data Capture,变更数据获取的简称,使用CDC我们可以从数据库中获取已提交的更改并将这些更改发送到下游,供下游使用。这些变更可以包括INSERT,DELETE,UPDATE等。用户可以在以下的场景下使用CDC: 使用f…...

SpingMvc入门
SpingMvc入门 1.MVC Spring的工作流程:2.sping mvc入门3.静态资源处理 前言 Spring MVC是一种基于Java的web应用开发框架,它采用了MVC(Model-View-Controller)设计模式来帮助开发者组织和管理应用程序的各个组件。 1.MVC Spring的…...
JVM的故事——类文件结构
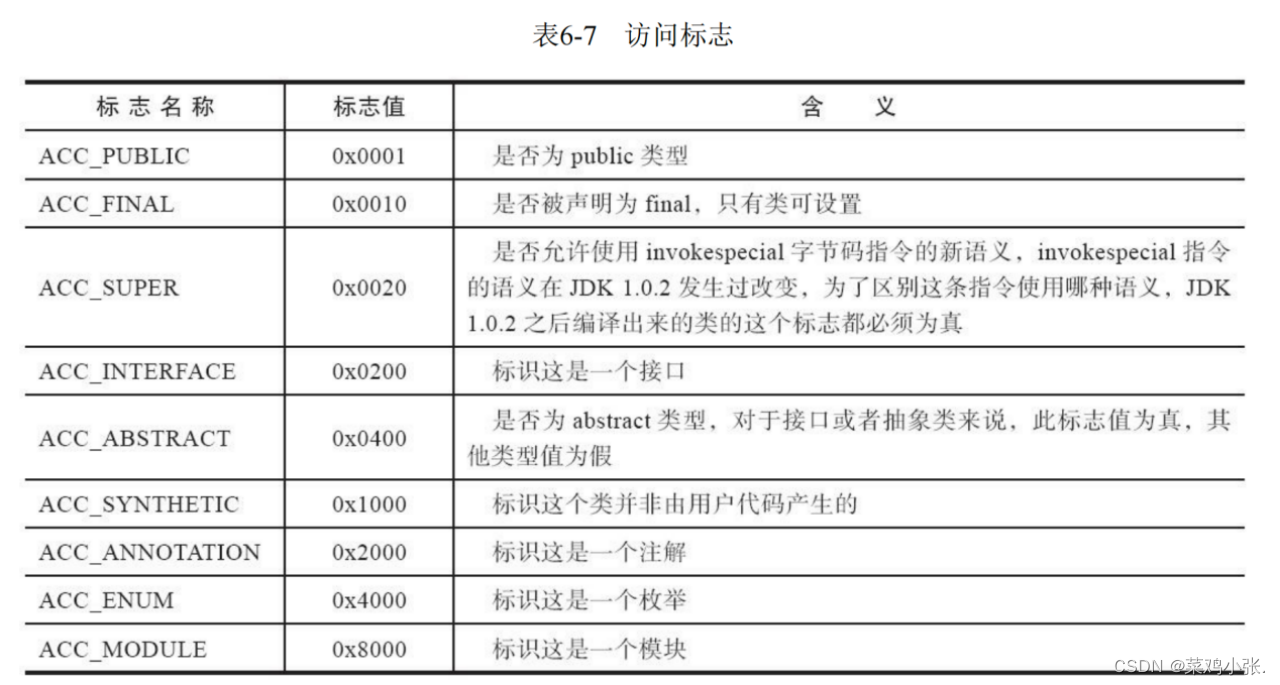
类文件结构 文章目录 类文件结构一、概述二、无关性基石三、Class类文件的结构 一、概述 计算机是只认由0、1组成的二进制码的,不过随着发展,我们编写的程序可以被编译成与指令集无关、平台中立的一种格式。 二、无关性基石 对于不同平台和不同平台的…...

springboot自定义表格(动态合并单元格)
一、需求展示(一个订单多个商品,商品数量不限订单行合并) 二、技术选型(jxls自定义模板) <!-- 版本具体看官网Release,这里我们使用 2.13.0 --><dependency><groupId>org.jxls</group…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
