OpenCV(十八):图像直方图
目录
1.直方图统计
2.直方图均衡化
3.直方图匹配
1.直方图统计
直方图统计是一种用于分析图像或数据的统计方法,它通过统计每个数值或像素值的频率分布来了解数据的分布情况。

在OpenCV中,可以使用函数cv::calcHist()来计算图像的直方图。
calcHist() 函数的原型如下:
void calcHist(const Mat* images, int nimages, const int* channels,
InputArray mask, OutputArray hist, int dims,
const int* histSize, const float** ranges,
bool uniform = true, bool accumulate = false);
参数说明:
-
images: 输入图像数组,可以是单张图像或多张图像的数组。
-
nimages: 输入图像的数量。
-
channels: 要计算直方图的通道索引数组。例如,对于灰度图像,只有一个通道,因此 channels 设置为 {0};而对于彩色图像,可以指定 {0, 1, 2} 对应于 B、G、R 三个通道。
-
mask: 掩码图像,用于指定计算直方图的区域。如果不需要使用掩码,可以传入空的 Mat()。
-
hist: 输出的直方图,用于存储计算结果。
-
dims: 直方图的维度,通常为 1。
-
histSize: 直方图的大小,即每个维度的条目数量。
-
ranges: 直方图的范围,可以使用 {0, 256} 表示像素值范围为 [0, 256)。
-
uniform: 指示直方图条目是否均匀分布,默认为 true。
-
accumulate: 指示是否累积直方图,默认为 false。
下面是一个示例代码,展示如何使用cv::calcHist()函数计算图像的直方图:
#include <opencv2/opencv.hpp>
void hist(Mat image){
// 定义直方图参数
int histSize = 256; // 直方图条目数量
const int channels[1]={0};//通道索引
float range[] = { 0, 256 }; // 像素值范围
const float* histRange = { range };
bool uniform = true; // 直方图条目是否均匀分布
bool accumulate = false; // 直方图是否累积
// 计算直方图
cv::Mat hist;
cv::calcHist(&image, 1, channels, cv::Mat(), hist, 1, &histSize, &histRange, uniform, accumulate);// 绘制直方图
int histWidth = 512;
int histHeight = 400;
int binWidth = cvRound((double)histWidth / histSize);
cv::Mat histImage(histHeight, histWidth, CV_8UC4, cv::Scalar(0, 0, 0));
cv::normalize(hist, hist, 0, histImage.rows, cv::NORM_MINMAX, -1, cv::Mat());
for (int i = 1; i < histSize; ++i){
cv::line(histImage, cv::Point(binWidth * (i - 1), histHeight - cvRound(hist.at<float>(i - 1))),
cv::Point(binWidth * (i), histHeight - cvRound(hist.at<float>(i))),
cv::Scalar(255, 255, 255), 2, 8, 0);
}
// 显示直方图
cv::imwrite("/sdcard/DCIM/histImage.jpg", histImage);
}示例代码中将原图像image转换为单通道灰度图像。然后定义了直方图的参数,包括直方图条目数量、像素值范围、均匀性和累积性。接下来使用 cv::calcHist() 函数计算了图像的直方图,存储在 hist 中。最后,通过绘制直方图数据到 histImage 中,实现了直方图的可视化。

2.直方图均衡化
直方图均衡化是一种用于增强图像对比度的图像处理技术。它通过重新分布图像像素值的频率分布来增强图像的亮度和细节。
在OpenCV中,可以使用cv::equalizeHist()函数来进行直方图均衡化。该函数的原型如下:
void equalizeHist(InputArray src, OutputArray dst);
参数说明:
-
src:需要直方图均衡化的CV 8UC1图像。
-
dst: 直方图均衡化后的输出图像,与src具有相同尺寸和数据类型
下面是一个示例代码,展示如何使用cv::equalizeHist()函数来进行直方图均衡化:
#include <opencv2/opencv.hpp>
void drawHist(Mat &hist,string name){//归一化并绘制直方图函数int histSize = 256; // 直方图条目数量// 绘制直方图int histWidth = 512;int histHeight = 400;int binWidth = cvRound((double)histWidth / histSize);cv::Mat histImage(histHeight, histWidth, CV_8UC4, cv::Scalar(0, 0, 0));cv::normalize(hist, hist, 0, histImage.rows, cv::NORM_MINMAX, -1, cv::Mat());for (int i = 1; i < histSize; ++i){cv::line(histImage, cv::Point(binWidth * (i - 1), histHeight - cvRound(hist.at<float>(i - 1))),cv::Point(binWidth * (i), histHeight - cvRound(hist.at<float>(i))),cv::Scalar(255, 255, 255), 2, 8, 0);}// 显示直方图cv::imwrite("/sdcard/DCIM/"+name+".jpg", histImage);}
void EqualImage(Mat image){//灰度化Mat gray;cvtColor(image,gray,COLOR_BGR2GRAY);//将灰度图进行直方图均衡化Mat equalImg;equalizeHist(gray,equalImg);cv::imwrite("/sdcard/DCIM/equalImg.jpg", equalImg);// 定义直方图参数int histSize = 256; // 直方图条目数量const int channels[1]={0};//通道索引float range[] = { 0, 256 }; // 像素值范围const float* histRange = { range };bool uniform = true; // 直方图条目是否均匀分布bool accumulate = false; // 直方图是否累积// 计算直方图cv::Mat hist;cv::calcHist(&equalImg, 1, channels, cv::Mat(), hist, 1, &histSize, &histRange, uniform, accumulate);drawHist(hist,"hist1");}示例代码中将原图像image转换为单通道灰度图像,然后将灰度图进行直方图均衡化,之后定义了直方图的参数,包括直方图条目数量、像素值范围、均匀性和累积性。接下来使用 cv::calcHist() 函数计算了图像的直方图,存储在 hist 中。最后,通过绘制直方图数据到 histImage 中,实现了直方图的可视化。

3.直方图匹配
直方图匹配(Histogram Matching)是一种图像处理技术,用于将一副图像的直方图映射到另一副图像上,从而使它们的亮度分布或颜色分布相似。该技术常用于图像增强、风格转换、颜色校正等应用中。
以下是一个使用OpenCV实现直方图匹配的示例代码:
#include <opencv2/opencv.hpp>
#include <iostream>using namespace cv;
using namespace std;void drawHist(Mat &hist,string name){//归一化并绘制直方图函数int histSize = 256; // 直方图条目数量// 绘制直方图int histWidth = 512;int histHeight = 400;int binWidth = cvRound((double)histWidth / histSize);cv::Mat histImage(histHeight, histWidth, CV_8UC4, cv::Scalar(0, 0, 0));cv::normalize(hist, hist, 0, histImage.rows, cv::NORM_MINMAX, -1, cv::Mat());for (int i = 1; i < histSize; ++i){cv::line(histImage, cv::Point(binWidth * (i - 1), histHeight - cvRound(hist.at<float>(i - 1))),cv::Point(binWidth * (i), histHeight - cvRound(hist.at<float>(i))),cv::Scalar(255, 255, 255), 2, 8, 0);}// 显示直方图cv::imwrite("/sdcard/DCIM/"+name+".jpg", histImage);}
void Histogram_matching(Mat img1,Mat img2){Mat hist1,hist2;//计算两张图像直方图const int channels[1]={0};float inRanges[2]={0,255};const float *ranges[1]={inRanges};const int bins[1]={256};calcHist(&img1,1,channels,Mat(),hist1,1,bins,ranges);calcHist(&img2,1,channels,Mat(),hist2,1,bins,ranges);//归一化两张图像的直方图drawHist(hist1,"hist1");drawHist(hist2,"hist2");//计算两张图像直方图的累计概率float hist1_cdf[256]={hist1.at<float>(0)};float hist2_cdf[256]={hist2.at<float>(0)};for(int i=1;i<256;i++){hist1_cdf[i]=hist1_cdf[i-1]+hist1.at<float>(i);hist2_cdf[i]=hist2_cdf[i-1]+hist1.at<float>(i);}//构建累积概率误差矩阵float diff_cdf[256][256];for(int i=0; i<256; i++){for(int j=0; j<256; j++){diff_cdf[i][j] = fabs(hist1_cdf[i] - hist2_cdf[j]);}}uchar lutone[256];for(int i=0;i<256;i++){//查找源灰度级为i的映射灰度//和i的累积概率差值最小的规定化灰度float min=diff_cdf[i][0];int index=0;//寻找累积概率误差矩阵中每一行中的最小值for(int j=1;j<256;j++){if(min>diff_cdf[i][j]){min=diff_cdf[i][j];index=j;}}lutone[i]=index;}//生成LUT映射表Mat lut(1,256,CV_8UC1,lutone);Mat result,hist3;LUT(img1,lut,result);imwrite("/sdcard/DCIM/result.png",result);calcHist(&result,1,channels,Mat(),hist3,1,bins,ranges);drawHist(hist3,"hist3");}示例代码:计算原始图像和目标图像的直方图,归一化直方图,计算累计直方图,构建累积概率误差矩阵,根据最小差值构建映射表,最后将原始图像的灰度级根据映射表调整为目标图像的灰度级。下面是原始图像和直方图匹配后图片,可以看出直方图匹配后的图片使得图像中的细节更加清晰可见。


原图 直方图匹配的结果
相关文章:

OpenCV(十八):图像直方图
目录 1.直方图统计 2.直方图均衡化 3.直方图匹配 1.直方图统计 直方图统计是一种用于分析图像或数据的统计方法,它通过统计每个数值或像素值的频率分布来了解数据的分布情况。 在OpenCV中,可以使用函数cv::calcHist()来计算图像的直方图。 calcHist(…...

mac pro 查看隐藏文件夹
在Mac上查看隐藏文件夹可以使用以下方法: 使用终端: 打开终端应用程序,位于“应用程序”文件夹的“实用工具”子文件夹中。 在终端中,输入以下命令,然后按回车键: defaults write com.apple.finder AppleS…...

软件测试/测试开发丨Selenium 高级定位 Xpath
点此获取更多相关资料 本文为霍格沃兹测试开发学社学员学习笔记分享 原文链接:https://ceshiren.com/t/topic/27036 一、xpath 基本概念 XPATH是一门在XML文档中查找信息的语言 XPATH使用路径表达式在XML文档中进行导航 XPATH的应用非常广泛,可以用于UI自…...
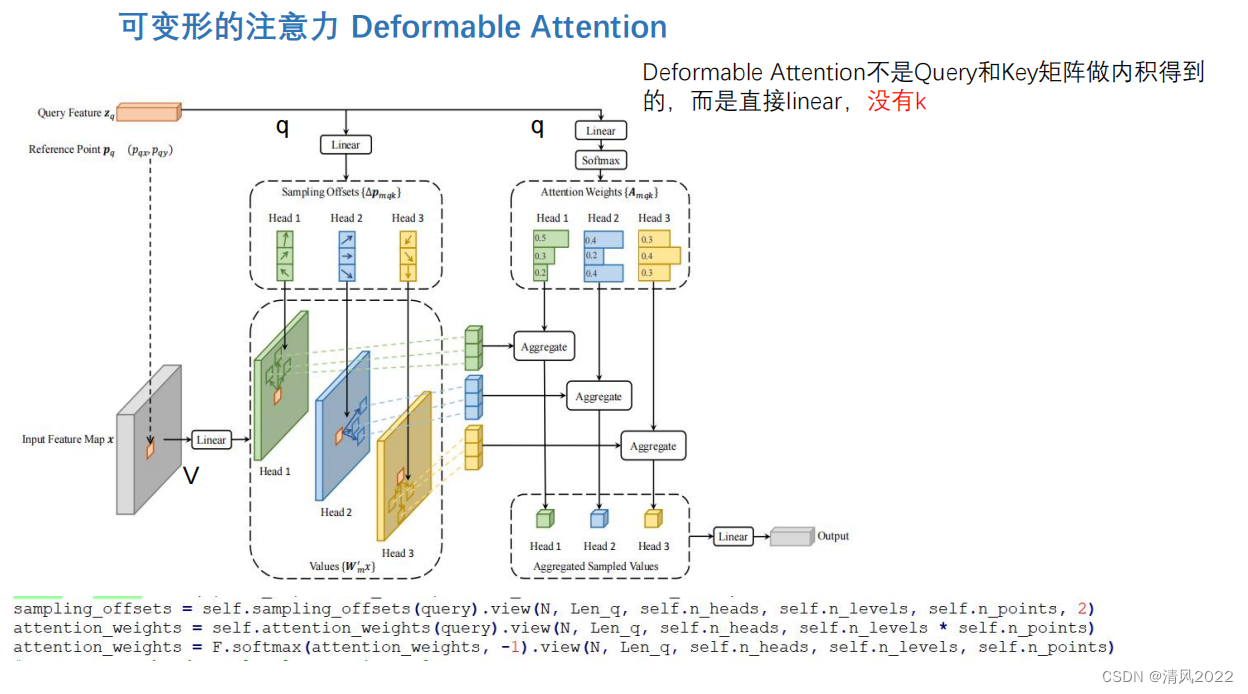
各类注意力机制Attention——可变形注意力
目录 《Attention is all you need 》稀疏Attention残差Attention通道注意力空间注意力时间注意力可变形注意力 《Attention is all you need 》 稀疏Attention 残差Attention 通道注意力 空间注意力 时间注意力 实际上序列类任务也属于时间注意力,比如transformer…...

桥接模式:连接抽象与实现
欢迎来到设计模式系列的第八篇文章!在之前的几篇文章中,我们已经学习了许多常见的设计模式,今天我们将继续探讨另一个重要的设计模式——桥接模式。 桥接模式简介 桥接模式是一种结构型设计模式,它主要用于将抽象部分与实现部分…...
同步推送?苹果计划本月推出 iOS17和iPadOS17,你的手机支持吗?
据报道,苹果公司计划在本月推出 iOS 17 和 iPadOS 17 正式版更新。与去年不同的是,这次更新将同时发布,而不是分别发布。根据彭博社的一位消息人士马克・古尔曼的说法,苹果公司认为 iOS 17 和 iPadOS 17 的第八个测试版已经非常接…...

方案展示 | RK3588开发板Linux双摄同显方案
iTOP-RK3588开发板使用手册更新,后续资料会不断更新,不断完善,帮助用户快速入门,大大提升研发速度。 RK3588开发板载4路MIPI CAMERA摄像头接口、MIPI CSI DPHY的4.5Gbps、2.5Gops的MIPI CSI CPHY,四路同时输入…...
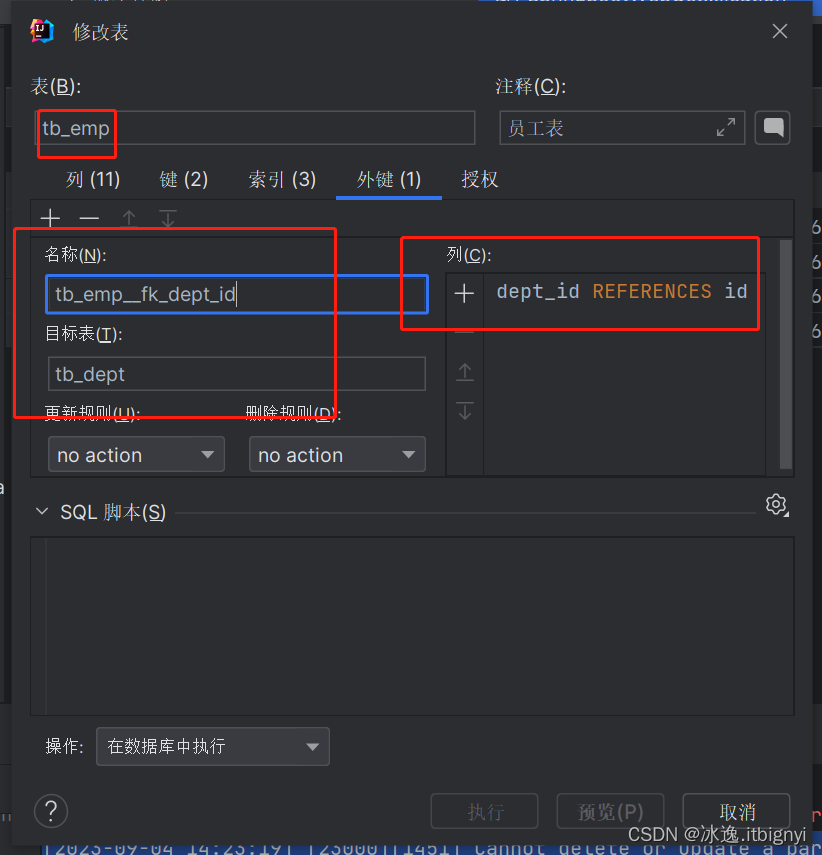
数据库-多表设计
概述: 项目开发中,在进行数据库表结构设计时,会根据业务需求及业务模块之间的关系,分析并设计表结构,由于业务之间相互关联,所以各个表结构之间也存在着各种联系,基本分为三种: 一对…...

一个简单的文件系统(MinixFS)实现解析
1. Minix文件系统概要 Minix file system 是 Andrew S. Tanenbaum 在 1980 年代发明的文件系统, 并随着 Minix 操作系统一起于 1987 年发布。 Linus 编写 Linux 内核第一个版本的时候, 使用的也是 Minix FS, Linux 至今依然提供了对 Minix FS 的支持。Minix FS 结构简单, 易于…...
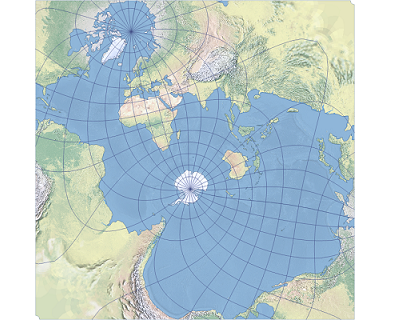
地图投影-2亚当斯方形
说明 亚当斯方形 II 投影显示了一个方形的世界。它是 Oscar S. Adams 于 1925 年提出的两种投影之一。该投影为等角投影,但方形的四个角除外。在 Adams 最初的设计中,该投影将赤道和中央经线显示为方形的对角线。 此投影的一个有利属性是可以进行细分或…...
floor_sum用法)
atcoder库中类欧(类欧几里得算法)floor_sum用法
https://atcoder.jp/contests/practice2/tasks/practice2_c 求 ∑ i 0 N − 1 f l o o r ( ( A i B ) / m ) \sum_{i 0}^{N - 1} floor((A \times i B) / m) ∑i0N−1floor((AiB)/m) 直接使用即可: ansfloor_sum(n, m, A, B); //注意顺序...

后端面试话术集锦第 十一 篇:mybatis面试话术
这是后端面试集锦第十一篇博文——mybatis面试话术❗❗❗ 1. 介绍下mybatis,说说它的优缺点是什么? Mybatis是一个半ORM(对象关系映射)的持久层框架,它内部封装了JDBC,开发时只需要关注SQL语句本身,不需要花费精力去处理加载驱动、创建连接、创建statement等繁杂的过程…...

SpringBoot运维实用篇、打包、运行、高级配置、多环境开发、日志
文章目录 SpringBoot运维实用篇YW-1.SpringBoot程序的打包与运行程序打包程序运行SpringBoot程序打包失败处理命令行启动常见问题及解决方案SpringBoot项目快速启动(Linux版) YW-2.配置高级YW-2-1.临时属性设置YW-2-2.配置文件分类YW-2-3.自定义配置文件…...
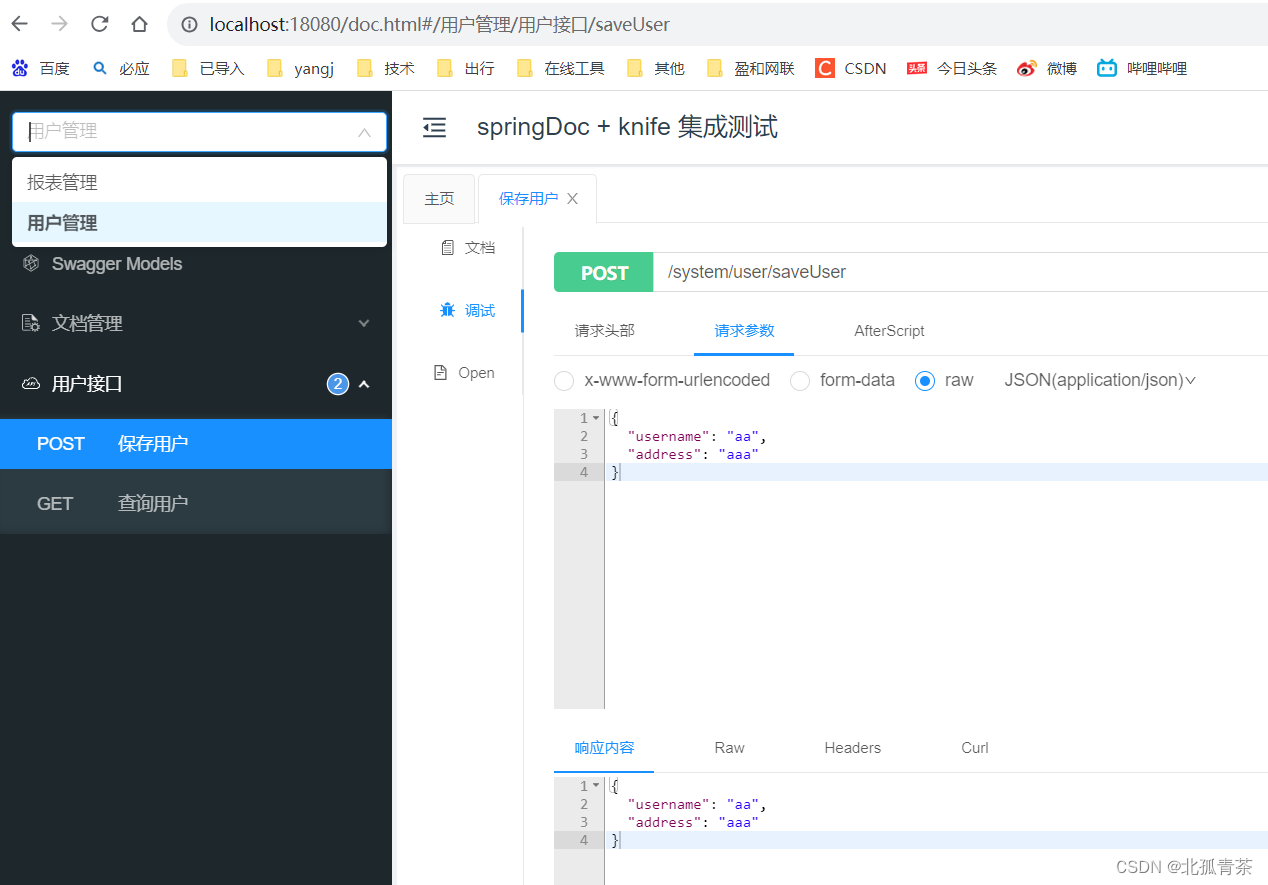
springdoc-openapi-ui 整合 knife,多模块分组,脚手架
pom文件: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.o…...
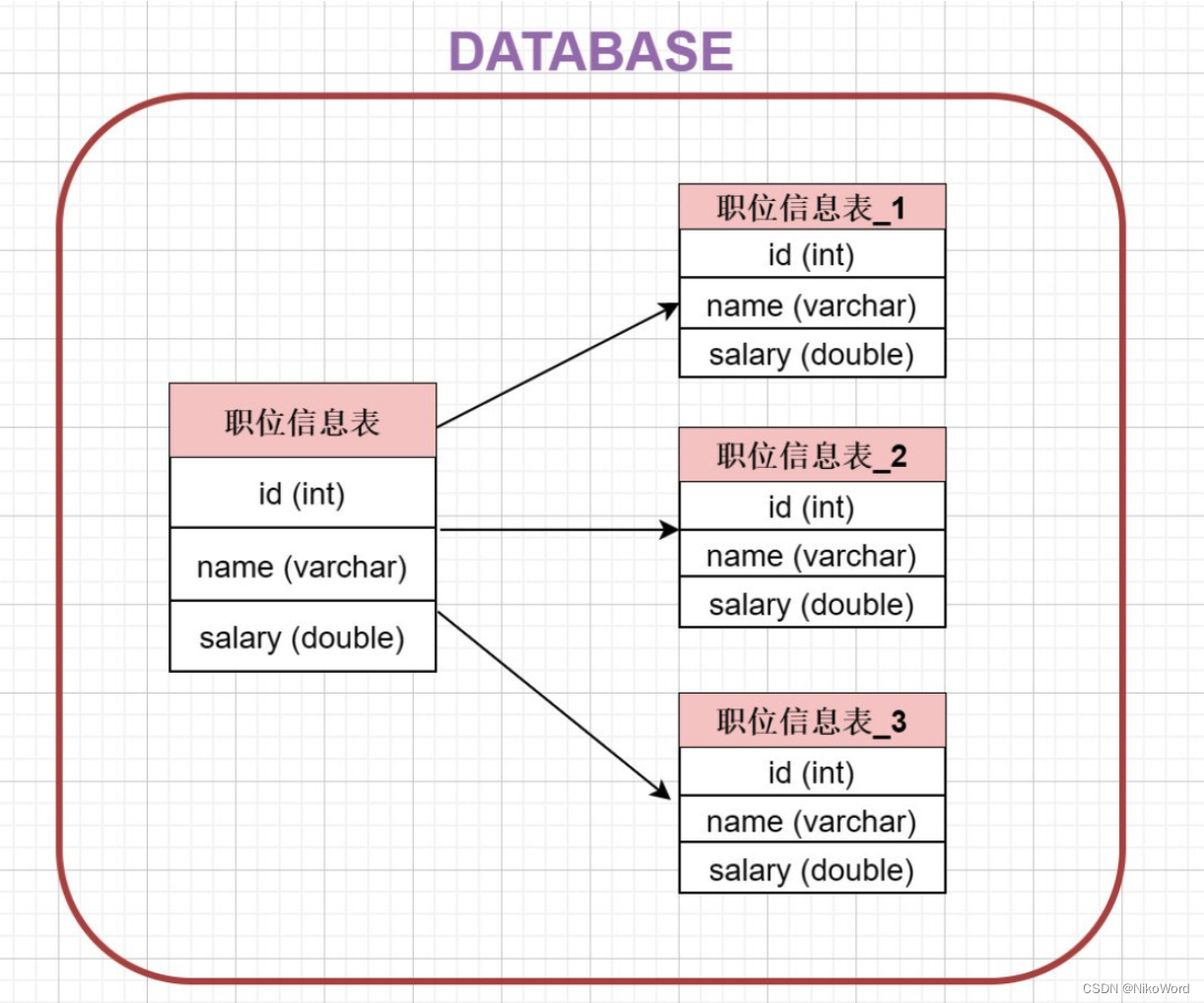
04-MySQL02
1、什么是索引下推? 索引下推(index condition pushdown )简称ICP,在Mysql5.6的版本上推出,用于优化查询。 需求: 查询users表中 "名字第一个字是张,年龄为10岁的所有记录"。 SELECT * FROM u…...

实现跨境电商测评和采退、LU卡、LU货最安全的系统方案
首先你要有一个稳定的测评环境系统,这个是做自养号退款、撸货、撸卡的基础。测评环境系统有很多,从早期的虚拟机,模拟机,云手机,VPS等等。这些系统方案先不说成本高,最重要的是成功率很低,所以一…...
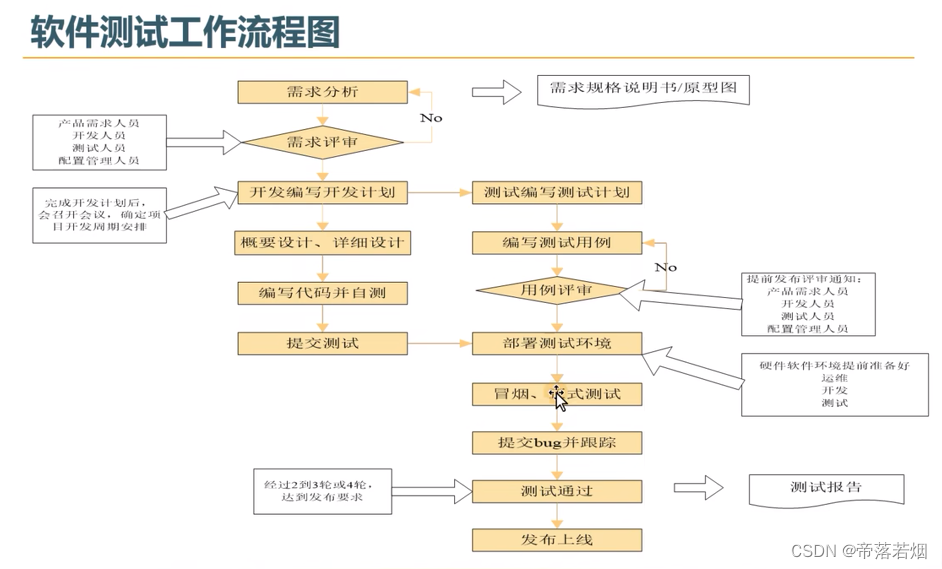
软件生命周期及流程
软件生命周期: 软件生命周期(SDLC,Systems Development Life Cycle)是软件开始研制到最终被废弃不用所经历的各个阶段. 需求分析阶段--输出需求规格说明书(原型图) 测试介入的晚--回溯成本高 敏捷开发模型: 从1990年…...

nginx使用详解
文章目录 一、前言二、nginx使用详解2.1、nginx特点2.2 静态文件处理2.3 反向代理2.4 负载均衡2.5 高级用法2.5.1 正则表达式匹配2.5.2 重定向 三、总结 一、前言 本文将详细介绍nginx的各个功能使用,主要包括 二、nginx使用详解 2.1、nginx特点 高性能ÿ…...

YOLOV7 添加 CBAM 注意力机制
用于学习记录 文章目录 前言一、CBAM1.1 models/common.py1.2 models/yolo.py1.3 yolov7/cfg/training/CBAM.yaml2.4 CBAM 训练结果图 前言 一、CBAM CBAM: Convolutional Block Attention Module 1.1 models/common.py class ChannelAttention(nn.Module):def __init__(sel…...
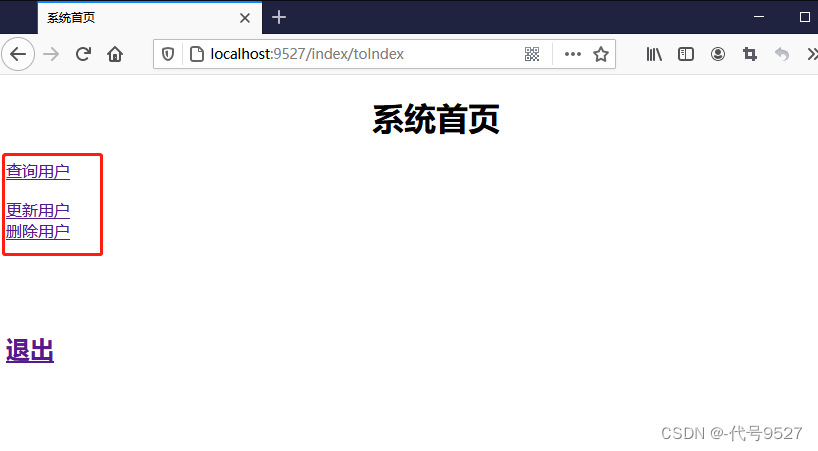
【SpringSecurity】七、SpringSecurity集成thymeleaf
文章目录 1、thymeleaf2、依赖部分3、定义Controller4、创建静态页面5、WebSecurityConfigurerAdapter6、权限相关7、当用户没有某权限时,页面不展示该按钮 1、thymeleaf 查了下读音,leaf/li:f/,叶子,前面的单词发音和时间time一…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...

Sklearn 机器学习 缺失值处理 获取填充失值的统计值
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 使用 Scikit-learn 处理缺失值并提取填充统计信息的完整指南 在机器学习项目中,数据清…...

【FTP】ftp文件传输会丢包吗?批量几百个文件传输,有一些文件没有传输完整,如何解决?
FTP(File Transfer Protocol)本身是一个基于 TCP 的协议,理论上不会丢包。但 FTP 文件传输过程中仍可能出现文件不完整、丢失或损坏的情况,主要原因包括: ✅ 一、FTP传输可能“丢包”或文件不完整的原因 原因描述网络…...

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...

HTML版英语学习系统
HTML版英语学习系统 这是一个完全免费、无需安装、功能完整的英语学习工具,使用HTML CSS JavaScript实现。 功能 文本朗读练习 - 输入英文文章,系统朗读帮助练习听力和发音,适合跟读练习,模仿学习;实时词典查询 - 双…...
