【高等数学基础知识篇】——不定积分
文章目录
- 一、不定积分的概念与基本性质
- 1.1 原函数与不定积分的基本概念
- 1.2 不定积分的基本性质
- 二、不定积分基本公式与积分法
- 2.1 不定积分基本公式
- 2.2 不定积分的积分法
- 2.2.1 换元积分法
- 2.2.2 分部积分法
- 三、两类重要函数的不定积分——有理函数与三角有理函数
- 3.1 有理函数的积分
- 3.2 三角有理函数的不定积分
一、不定积分的概念与基本性质
1.1 原函数与不定积分的基本概念
划重点
- 连续函数一定存在原函数,反之不对。
- 有第一类间断点的函数一定不存在原函数,但有第二肋间断点的函数可能有原函数。
- 若f(x)有原函数,则它一定有无数个原函数,且任意两个原函数之间相差常数。
- 偶函数的原函数不一定是奇函数,奇函数的原函数一定是偶函数。
1.2 不定积分的基本性质
- ∫ [ f ( x ) ± g ( x ) ] d x \int[f(x) ± g(x)]dx ∫[f(x)±g(x)]dx = ∫ f ( x ) d x ± ∫ g ( x ) d x \int f(x)dx ± \int g(x)dx ∫f(x)dx±∫g(x)dx
- ∫ k f ( x ) d x \int kf(x)dx ∫kf(x)dx = k ∫ f ( x ) d x \int f(x)dx ∫f(x)dx(k ≠ 0)
二、不定积分基本公式与积分法
2.1 不定积分基本公式
| 不定积分 | 原函数 |
|---|---|
| ∫ k d x \int kdx ∫kdx | kx + C |
| ∫ x a d x \int x\ ^adx ∫x adx | 1 a + 1 x a + 1 \frac{1}{a + 1}x\ ^{a + 1} a+11x a+1 + C |
| ∫ 1 x d x \int \frac{1}{x}dx ∫x1dx | ln|x| + C(x ≠ 0) |
| ∫ a x d x \int a\ ^xdx ∫a xdx | a x l n a \frac{a\ ^x}{ln a} lnaa x + C(a > 0,a ≠ 1) |
| ∫ e x d x \int e\ ^xdx ∫e xdx | ex + C |
| ∫ s i n x d x \int sin xdx ∫sinxdx | -cos x + C |
| ∫ c o s x d x \int cos xdx ∫cosxdx | sin x + C |
| ∫ t a n t x d x \int tant xdx ∫tantxdx | -ln|cos x| + C |
| ∫ c o t x d x \int cot xdx ∫cotxdx | ln|sin x| + C |
| ∫ s e c x d x \int sec xdx ∫secxdx | ln|sec x + tan x| + C |
| ∫ c s c x d x \int csc xdx ∫cscxdx | ln|csc x - cot x| + C |
| ∫ s e c 2 x d x \int sec\ ^2xdx ∫sec 2xdx | tan x + C |
| ∫ c s c 2 x d x \int csc\ ^2xdx ∫csc 2xdx | -cot x + C |
| ∫ s e c x t a n x d x \int sec xtan xdx ∫secxtanxdx | sec x + C |
| ∫ c s c x c o t x d x \int csc xcot xdx ∫cscxcotxdx | -csc x + C |
| ∫ d x 1 − x 2 \int \frac{dx}{\sqrt[]{1 - x\ ^2}} ∫1−x 2dx | arcsin x + C |
| ∫ d x a 2 − x 2 \int \frac{dx}{\sqrt[]{a\ ^2 - x\ ^2}} ∫a 2−x 2dx | arcsin x a \frac{x}{a} ax + C(a > 0) |
| ∫ d x 1 + x 2 \int \frac{dx}{1 + x\ ^2} ∫1+x 2dx | arctan x + C |
| ∫ d x a 2 + x 2 \int \frac{dx}{a\ ^2 + x\ ^2} ∫a 2+x 2dx | 1 a a r c t a n x a \frac{1}{a}arctan\frac{x}{a} a1arctanax + C(a ≠ 0) |
| ∫ d x x 2 − a 2 \int \frac{dx}{x\ ^2 - a\ ^2} ∫x 2−a 2dx | 1 2 a l n ∣ x − a x + a ∣ \frac{1}{2a}ln|\frac{x - a}{x + a}| 2a1ln∣x+ax−a∣ + C(a ≠ 0) |
| ∫ d x x 2 + a 2 \int \frac{dx}{\sqrt[]{x\ ^2 + a\ ^2}} ∫x 2+a 2dx | ln(x + x 2 + a 2 \sqrt[]{x\ ^2 + a\ ^2} x 2+a 2) + C |
| ∫ d x x 2 − a 2 \int \frac{dx}{\sqrt[]{x\ ^2 - a\ ^2}} ∫x 2−a 2dx | ln|x + x 2 − a 2 \sqrt[]{x\ ^2 - a\ ^2} x 2−a 2\ + C |
| ∫ a 2 − x 2 d x \int \sqrt[]{a\ ^2 - x\ ^2}dx ∫a 2−x 2dx | a 2 2 a r c s i n x a + x 2 a 2 − x 2 \frac{a\ ^2}{2}arcsin\frac{x}{a} + \frac{x}{2}\sqrt[]{a\ ^2 - x\ ^2} 2a 2arcsinax+2xa 2−x 2 + C(a > 0) |
2.2 不定积分的积分法
2.2.1 换元积分法
第一类换元积分法(凑微分法)
设f(u)的原函数为F(u),且u = φ(x)为可导函数,则
∫ f [ φ ( x ) ] φ ′ ( x ) d x \int f[φ(x)]φ'(x)dx ∫f[φ(x)]φ′(x)dx = ∫ f [ φ ( x ) ] d [ φ ( x ) ] \int f[φ(x)]d[φ(x)] ∫f[φ(x)]d[φ(x)] = ∫ f ( u ) d u \int f(u)du ∫f(u)du = F(u) + C = F[φ(x)] + C。
以下凑微分法需要熟练掌握
| 原积分 | 凑微分法 |
|---|---|
| ∫ f ( a x n + b ) x n − 1 d x \int f(ax\ ^n + b)x\ ^{n - 1}dx ∫f(ax n+b)x n−1dx | 1 n a ∫ f ( a x n + b ) d ( a x n + b ) \frac{1}{na}\int f(ax\ ^n + b)d(ax\ ^n + b) na1∫f(ax n+b)d(ax n+b) |
| ∫ f ( x ) 2 x d x \int \frac{f(\sqrt[]{x})}{2\sqrt[]{x}}dx ∫2xf(x)dx | ∫ f ( x ) d x \int f(\sqrt[]{x})d\sqrt[]{x} ∫f(x)dx |
| ∫ 1 x 2 f ( 1 x ) d x \int \frac{1}{x\ ^2}f(\frac{1}{x})dx ∫x 21f(x1)dx | - ∫ f ( 1 x ) d ( 1 x ) \int f(\frac{1}{x})d(\frac{1}{x}) ∫f(x1)d(x1) |
| ∫ e x f ( e x ) d x \int e\ ^xf(e\ ^x)dx ∫e xf(e x)dx | ∫ f ( e x ) d ( e x ) \int f(e\ ^x)d(e\ ^x) ∫f(e x)d(e x) |
| ∫ f ( l n x ) x d x \int \frac{f(ln x)}{x}dx ∫xf(lnx)dx | ∫ f ( l n x ) d ( l n x ) \int f(ln x)d(ln x) ∫f(lnx)d(lnx) |
| ∫ ( 1 − 1 x 2 ) f ( x + 1 x ) d x \int (1 - \frac{1}{x\ ^2})f(x + \frac{1}{x})dx ∫(1−x 21)f(x+x1)dx | ∫ f ( x + 1 x ) d ( x + 1 x ) \int f(x + \frac{1}{x})d(x + \frac{1}{x}) ∫f(x+x1)d(x+x1) |
| ∫ ( 1 + 1 x 2 ) f ( x − 1 x ) d x \int (1 + \frac{1}{x\ ^2})f(x - \frac{1}{x})dx ∫(1+x 21)f(x−x1)dx | ∫ f ( x − 1 x ) d ( x − 1 x ) \int f(x - \frac{1}{x})d(x - \frac{1}{x}) ∫f(x−x1)d(x−x1) |
| ∫ ( 1 + l n x ) f ( x l n x ) d x \int (1 + ln x)f(xln x)dx ∫(1+lnx)f(xlnx)dx | ∫ f ( x l n x ) d ( x l n x ) \int f(xln x)d(xln x) ∫f(xlnx)d(xlnx) |
| ∫ f ( s i n x ) c o s x d x \int f(sin x)cos xdx ∫f(sinx)cosxdx | ∫ f ( s i n x ) d ( s i n x ) \int f(sin x)d(sin x) ∫f(sinx)d(sinx) |
| ∫ f ( c o s x ) s i n x d x \int f(cos x)sin xdx ∫f(cosx)sinxdx | - ∫ f ( c o s x ) d ( c o s x ) \int f(cos x)d(cos x) ∫f(cosx)d(cosx) |
| ∫ f ( t a n x ) s e c 2 x d x \int f(tan x)sec\ ^2xdx ∫f(tanx)sec 2xdx | ∫ f ( t a n x ) d ( t a n x ) \int f(tan x)d(tan x) ∫f(tanx)d(tanx) |
| ∫ f ( c o t x ) c s c 2 x d x \int f(cot x)csc\ ^2xdx ∫f(cotx)csc 2xdx | - ∫ f ( c o t x ) d ( c o t x ) \int f(cot x)d(cot x) ∫f(cotx)d(cotx) |
| ∫ f ( s e c x ) s e c x t a n x d x \int f(sec x)sec xtan xdx ∫f(secx)secxtanxdx | ∫ f ( s e c x ) d ( s e c x ) \int f(sec x)d(sec x) ∫f(secx)d(secx) |
| ∫ f ( c s c x ) c s c x c o t x d x \int f(csc x)csc xcot xdx ∫f(cscx)cscxcotxdx | - ∫ f ( c s c x ) d ( c s c x ) \int f(csc x)d(csc x) ∫f(cscx)d(cscx) |
| ∫ f ( a r c s i n x ) 1 − x 2 d x \int \frac{f(arcsin x)}{\sqrt[]{1 - x\ ^2}}dx ∫1−x 2f(arcsinx)dx | ∫ f ( a r c s i n x ) d ( a r c s i n x ) \int f(arcsin x)d(arcsin x) ∫f(arcsinx)d(arcsinx) |
| ∫ f ( a r c t a n x ) 1 + x 2 d x \int \frac{f(arctan x)}{1 + x\ ^2}dx ∫1+x 2f(arctanx)dx | ∫ f ( a r c t a n x ) d ( a r c t a n x ) \int f(arctan x)d(arctan x) ∫f(arctanx)d(arctanx) |
第二类换元积分法
设φ(t)单调可导且φ’(t) ≠ 0,f(x)有原函数,则
∫ f ( x ) d x \int f(x)dx ∫f(x)dx = ∫ f [ φ ( t ) ] φ ′ ( t ) d t \int f[φ(t)]φ'(t)dt ∫f[φ(t)]φ′(t)dt = ∫ g ( t ) d t \int g(t)dt ∫g(t)dt = G(t) + C = G[ φ − 1 φ\ ^{-1} φ −1(x)] + C。
当被积函数含平方和或平方差是,一般采用三角代换,具体换元方法为
| 表达式 | 替换式 |
|---|---|
| a 2 − x 2 a\ ^2 - x\ ^2 a 2−x 2 | 令x = asin t,则 a 2 − x 2 = a 2 c o s 2 t a\ ^2 - x\ ^2 = a\ ^2cos\ ^2t a 2−x 2=a 2cos 2t |
| x 2 + a 2 x\ ^2 + a\ ^2 x 2+a 2 | 令x = atan t,则 x 2 + a 2 = a 2 s e c 2 t x\ ^2 + a\ ^2 = a\ ^2sec\ ^2t x 2+a 2=a 2sec 2t |
| x 2 − a 2 x\ ^2 - a\ ^2 x 2−a 2 | 令x = asec t,则 x 2 − a 2 = a 2 t a n 2 t x\ ^2 - a\ ^2 = a\ ^2tan\ ^2t x 2−a 2=a 2tan 2t |
倒数变换x = 1 t \frac{1}{t} t1
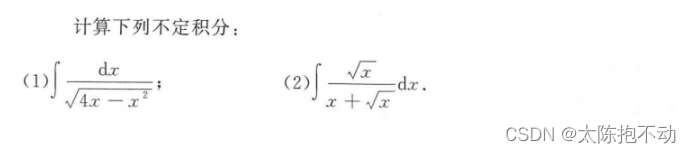
遇到 x \sqrt[]{x} x,想办法转换称d( x \sqrt[]{x} x)。
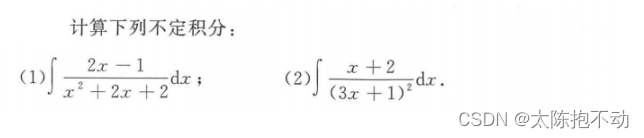

2.2.2 分部积分法
设u(x),v(x)连续可导,则分布积分公式为 ∫ u d v \int udv ∫udv = uv - ∫ v d u \int vdu ∫vdu。
以下六种情况使用分部积分公式
- ∫ x n e x d x \int x\ ^ne\ ^xdx ∫x ne xdx,即被积函数为幂函数与指数函数之积。
- ∫ x n l n x d x \int x\ ^nln xdx ∫x nlnxdx,即被积函数为幂函数与指数函数之积。
- 被积函数为幂函数与三角函数之积。
- 被积函数为幂函数与反三角函数之积。
- 被积函数为指数函数与三角函数之积。
- 被积函数为 s e c n x sec\ ^nx sec nx或 c s c n x csc\ ^nx csc nx(n为奇数)。
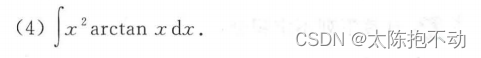
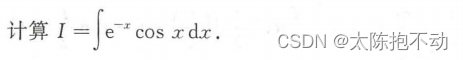
三、两类重要函数的不定积分——有理函数与三角有理函数
3.1 有理函数的积分
有理函数的概念
设R(x) = P ( x ) Q ( x ) \frac{P(x)}{Q(x)} Q(x)P(x),其中P(x),Q(x)为多项式,称R(x)为有理函数。当分子多项式P(x)的次数小于分母多项式Q(x)的次数时,称R(x)为真分式。否则,称为假分式。
有理函数的积分法
- 当R(x)为真分式时,将R(x)拆分成部分和的形式。
- 当R(x)为假分式时,将R(x)拆成多项式与真分式之和,再将真分式拆成部分和的形式。
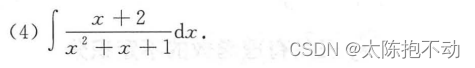
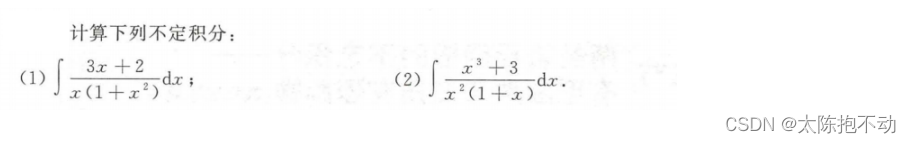
本题需要明确有理函数的拆分方法。拆分时需要关注x的幂次以及是单根还是重根。以本题为例,说明以下拆分方法。
关注x的幂次
例如, 3 x + 2 x ( 1 + x 2 ) \frac{3x + 2}{x(1 + x\ ^2)} x(1+x 2)3x+2,可以拆分成 A x \frac{A}{x} xA + B x + C 1 + x 2 \frac{Bx + C}{1 + x\ ^2} 1+x 2Bx+C。
关注是单根还是重根
例如, x 3 + 3 x 2 ( 1 + x ) \frac{x\ ^3 + 3}{x\ ^2(1 + x)} x 2(1+x)x 3+3,可以拆分成 A x \frac{A}{x} xA + B x 2 \frac{B}{x\ ^2} x 2B + C 1 + x \frac{C}{1 + x} 1+xC。
其实还有复数根的情况,这里没有遇到,暂不做介绍,后续遇到会进行补充。
3.2 三角有理函数的不定积分
三角有理函数的概念
设R(x,y)为二元有理函数,称R(sin x,cos x)为三角有理函数。
相关文章:
【高等数学基础知识篇】——不定积分
文章目录 一、不定积分的概念与基本性质1.1 原函数与不定积分的基本概念1.2 不定积分的基本性质 二、不定积分基本公式与积分法2.1 不定积分基本公式2.2 不定积分的积分法2.2.1 换元积分法2.2.2 分部积分法 三、两类重要函数的不定积分——有理函数与三角有理函数3.1 有理函数的…...

python使用鼠标在图片上画框
python rect.py 图片文件夹先左击左上角,再右击右下角,画出一个框结果保存在res文件夹rect.py import cv2, sys, ospathsys.argv[1] imcv2.imread(path) alos.listdir(path) al.sort() if not os.path.exists(res): os.makedirs(res)def getInfo(event,…...

算法通关村第十五关:青铜-用4KB内存寻找重复元素
青铜挑战-用4KB内存寻找重复元素 位运算在查找元素中的妙用 题目要求: 给定一个数组,包含从1到N的整数,N最大为32000,数组可能还有重复值,且N的取值不定,若只有4KB的内存可用,该如何打印数组中…...
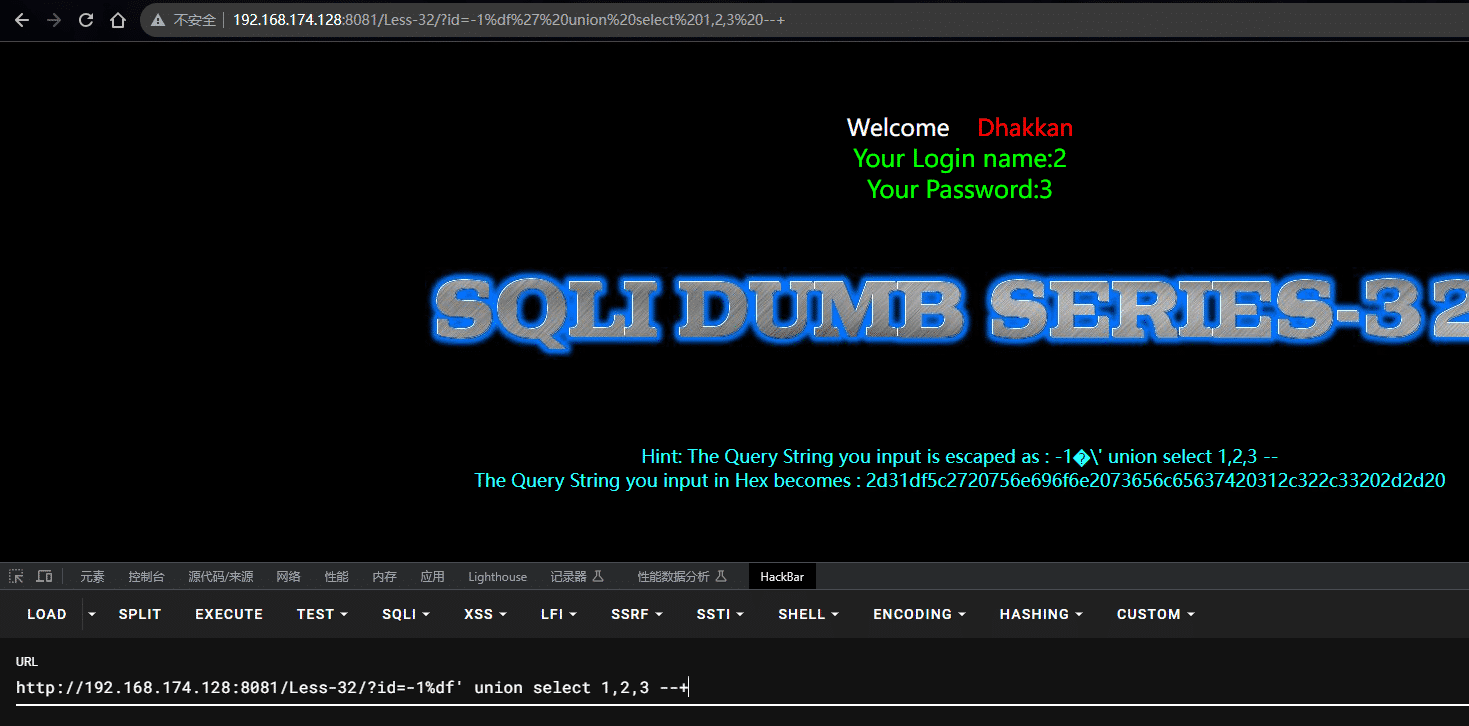
SQL注入 - 宽字节注入
文章目录 SQL注入 - 宽字节注入宽字节注入前置知识宽字节靶场实战判断是否存在SQL注入判断位数判显错位判库名判表名判列名 SQL注入 - 宽字节注入 靶场 sqli - labs less-32 宽字节注入主要是绕过魔术引号的,数据库解析中除了UTF-8编码外的所有编码如:G…...
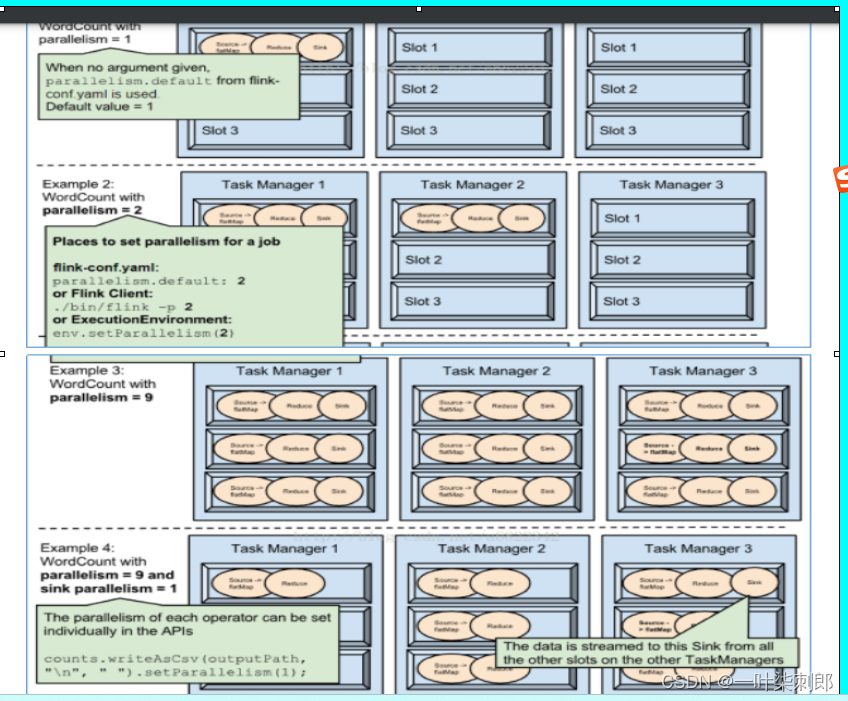
Flink基础
Flink architecture job manager is master task managers are workers task slot is a unit of resource in cluster, number of slot is equal to number of cores(超线程则slot2*cores), slot一组内存一些线程共享CPU when starting a cluster,job manager will allocate a …...
javaee spring aop 注解实现
切面类 package com.test.advice;import org.aspectj.lang.ProceedingJoinPoint; import org.aspectj.lang.annotation.*;//切面类 Aspect public class MyAdvice {//定义切点表达式Pointcut("execution(* com.test.service.impl.*.add(..))")public void pc(){}//B…...
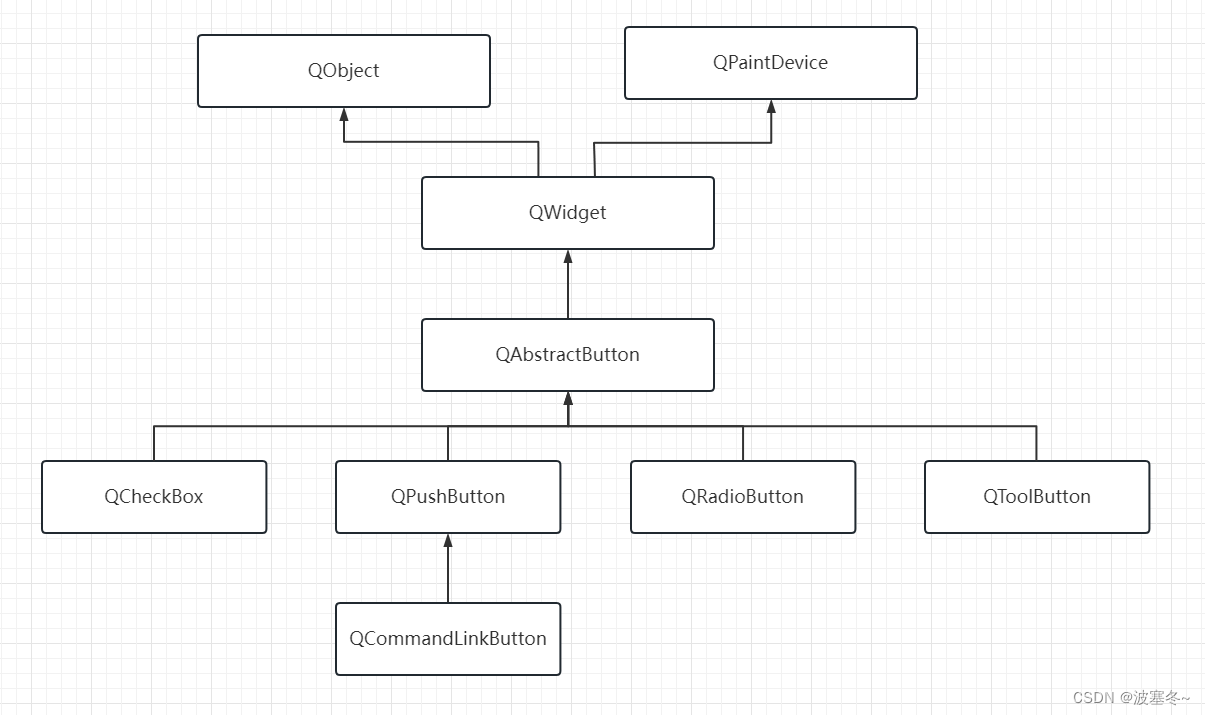
Qt应用开发(基础篇)——按钮基类 QAbstractButton
一、前言 QAbstractButton类,继承于QWidget,是Qt按钮小部件的抽象基类,提供按钮常用的功能。 QAbstractButton按钮基类,它的子类(pushbutton、checkbox、toolbutton等)处理用户操作,并指定按钮的绘制方式。QAbstractBu…...
)
2023年最新的 前端面试题(个人总结)
目录 vue 1.vue2 和 vue3 的区别 2.vue2 和 vue3的原理 3.组合式api 和 选项式api 3. Proxy和object.defineproperty 4..v-show 与 v-if 的区别 5.计算属性和 watcher 6.虚拟DOM 7.key的作用是什么? 8.v-if 和 v-for 的优先级是什么? 9.vuex …...

服务器基本故障排查方法
1、加电类故障 定义 从上电(或复位)到自检完成这一段过程中电脑所发生的故障。可能的故障现象 1、 主机不能加电(如:电源风扇不转或转一下即停等)、有时不能加电、开机掉闸、机箱金属部分带电等; 2、 开机无显,开机报警; 3、 自检报错或死机、自检过程中…...
docker从零部署jenkins保姆级教程
jenkins,基本是最常用的持续集成工具。在实际的工作中,后端研发一般没有jenkins的操作权限,只有一些查看权限,但是我们的代码是经过这个工具构建出来部署到服务器的,所以我觉着有必要了解一下这个工具的搭建过程以及简…...

什么是 MVVM 模式?
MVVM 模式 官方解释:Vue 虽然没有完全遵循 MVVM 模型,但是 Vue 的设计也受到了它的启发。因此在文档中经常会使用 vm (ViewModel 的缩写) 这个变量名表示 Vue 实例。 什么是 MVVM 模式? MVVM 是一种新的开发模式,对比传统模式&…...

WebGL Varing变量的作用和内插过程,及执行Varing时涉及的图形装配、光栅化、颜色插值、片元着色器执行机制等详解
目录 前言 在 WebGL 或 OpenGL 中,“varying” 是一种用于在顶点着色器和片元着色器之间传递数据的特殊类型的变量。它允许在顶点着色器对数据进行处理后,在片元着色器中使用该处理后的数据进行进一步计算。 彩色三个点 编辑 彩色三个点示例代码…...

赢在起跑线:战略定位咨询带来的核心价值
在企业的发展之路上,三个核心问题始终伴随着我们:我们是谁?我们要做什么?我们要如何做?在业务的马拉松比赛中,开始时的位置至关重要。而战略定位咨询就是帮助企业赢在起跑线的关键。那么什么是战略定位?战略定位包含…...
【链表OJ 11】复制带随机指针的链表
前言: 💥🎈个人主页:Dream_Chaser~ 🎈💥 ✨✨刷题专栏:http://t.csdn.cn/UlvTc ⛳⛳本篇内容:力扣上链表OJ题目 目录 leetcode138. 复制带随机指针的链表 1. 问题描述 2.代码思路: 2.1拷贝节点插入到…...
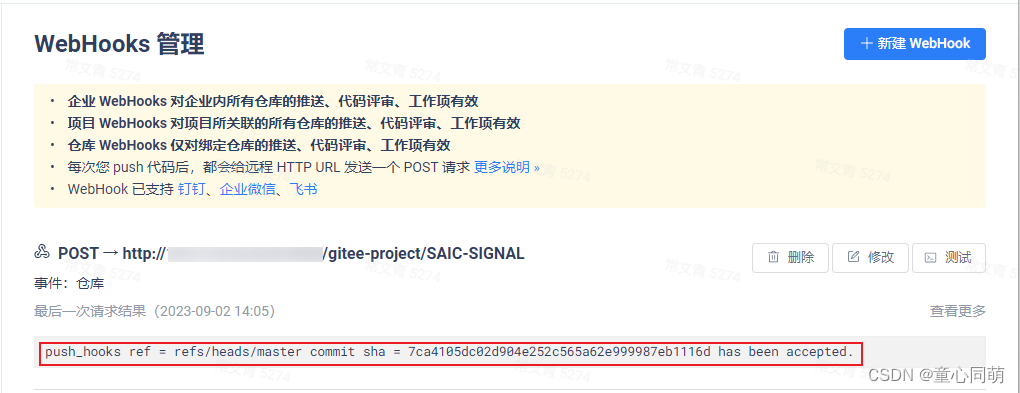
Jenkins自动构建(Gitee)
Gitee简介安装JenkinsCLI https://blog.csdn.net/tongxin_tongmeng/article/details/132632743 安装Gitee jenkins-cli install-plugin gitee:1.2.7 # https://plugins.jenkins.io/gitee/releases获取安装命令(稍作变更) JenkinsURL Dashboard-->配置-->Jenkins Locatio…...
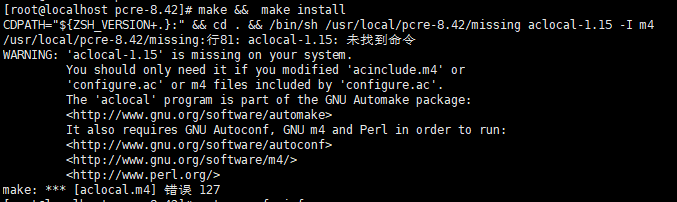
nginx离线安装
ngixn的离线安装(centos7) 需要的依赖 gcc、gcc-c pcre-8.42.tar.gz zlib-1.2.11.tar.gz openssl-1.1.1s.tar.gz perl-5.28.0.tar.gz 在进行nginx离线安装时,首先查看系统是否安装 gcc、gcc-c,若没有进行安装,请先进行安装 gcc -v #查…...

Oracle Merge Into ORA-00001: unique constaint violated问题
最近使用Datax同步进行定时数据同步,并在同步完之后进行回调sql进行统计操作。对应的ORACLE表结构如下: create table DATA_STAT_DAY ( DATA_DATE DATE, ID VARCHAR2(2), NAME VARCHAR2(2), CLASSNO VARCHAR2(2), SCORES NUMBER(16,0) );CREATE UNIQU…...
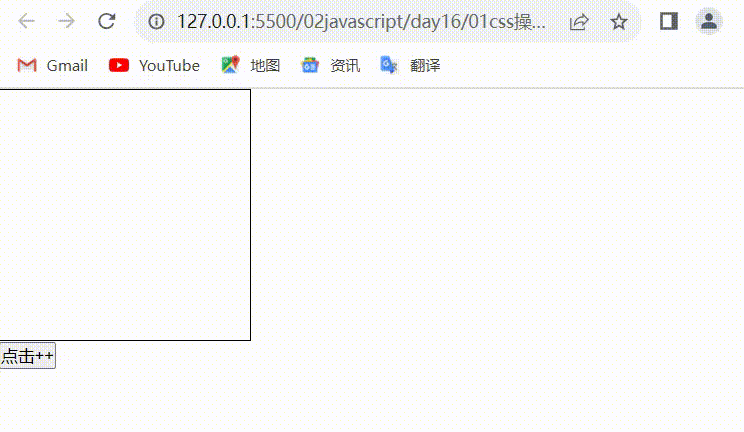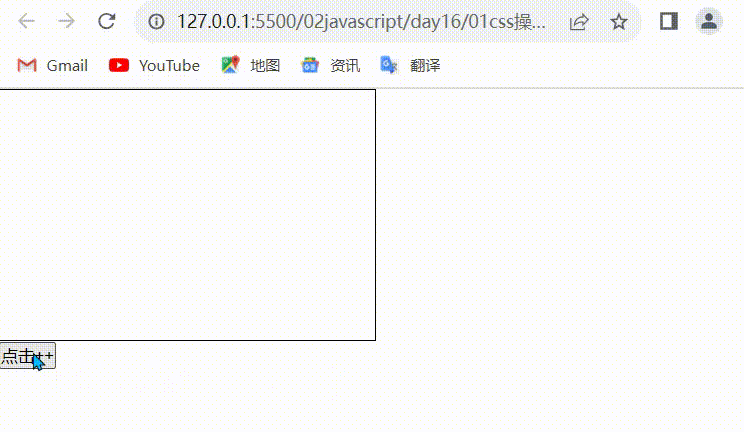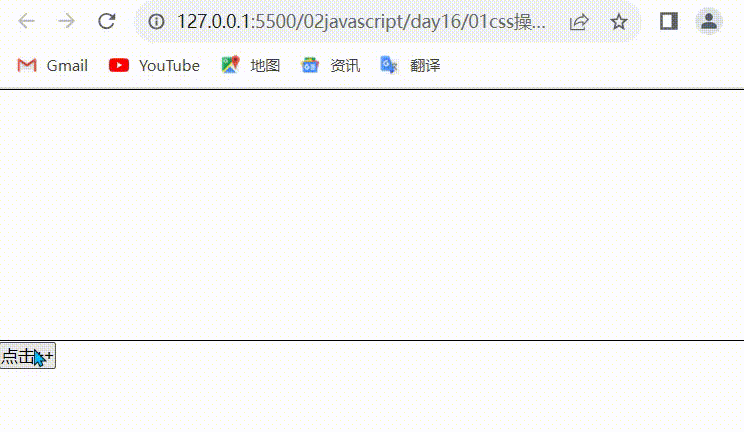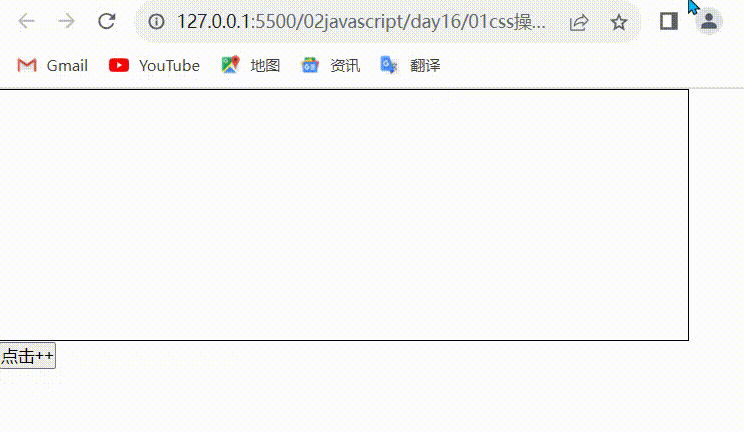
javaScript:DOM中的CSS操作
目录 1.style 属性获取元素写在行间的样式 2.getComputedStyle(元素对象,null)可以获取元素的非行间样式 3.案例(定义一个div和按钮,每点击一次按钮div宽度增加) 效果预览图 代码实现 在 JavaScript 中,可以通过…...

2023最新UI工作室官网个人主页源码/背景音乐/随机壁纸/一言
2023最新UI工作室官网个人主页源码/支持背景音乐/随机壁纸/一言 功能介绍: 载入动画 站点简介 Hitokoto 一言 日期及时间 实时天气 时光进度条 音乐播放器 移动端适配 打开文件;index.html和setting.json修改替换你的相关信息&a…...

常用命令之mysql命令之show命令
一、mysql show命令简介 mysql数据库中show命令是一个非常实用的命令,SHOW命令用于显示MySQL数据库中的信息。它可以用于显示数据库、表、列、索引和用户等各种对象的信息。我们常用的有show databases,show tables,show full processlist等&…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

【JavaEE】-- HTTP
1. HTTP是什么? HTTP(全称为"超文本传输协议")是一种应用非常广泛的应用层协议,HTTP是基于TCP协议的一种应用层协议。 应用层协议:是计算机网络协议栈中最高层的协议,它定义了运行在不同主机上…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...
