一文速学-让神经网络不再神秘,一天速学神经网络基础(七)-基于误差的反向传播
前言
思索了很久到底要不要出深度学习内容,毕竟在数学建模专栏里边的机器学习内容还有一大半算法没有更新,很多坑都没有填满,而且现在深度学习的文章和学习课程都十分的多,我考虑了很久决定还是得出神经网络系列文章,不然如果以后数学建模竞赛或者是其他更优化模型如果用上了神经网络(比如利用LSTM进行时间序列模型预测),那么就更好向大家解释并且阐述原理了。但是深度学习的内容不是那么好掌握的,包含大量的数学理论知识以及大量的计算公式原理需要推理。且如果不进行实际操作很难够理解我们写的代码究极在神经网络计算框架中代表什么作用。不过我会尽可能将知识简化,转换为我们比较熟悉的内容,我将尽力让大家了解并熟悉神经网络框架,保证能够理解通畅以及推演顺利的条件之下,尽量不使用过多的数学公式和专业理论知识。以一篇文章快速了解并实现该算法,以效率最高的方式熟练这些知识。
现在很多竞赛虽然没有限定使用算法框架,但是更多获奖的队伍都使用到了深度学习算法,传统机器学习算法日渐式微。比如2022美国大学生数学建模C题,参数队伍使用到了深度学习网络的队伍,获奖比例都非常高,现在人工智能比赛和数据挖掘比赛都相继增多,对神经网络知识需求也日渐增多,因此十分有必要掌握各类神经网络算法。
博主专注建模四年,参与过大大小小数十来次数学建模,理解各类模型原理以及每种模型的建模流程和各类题目分析方法。此专栏的目的就是为了让零基础快速使用各类数学模型、机器学习和深度学习以及代码,每一篇文章都包含实战项目以及可运行代码。博主紧跟各类数模比赛,每场数模竞赛博主都会将最新的思路和代码写进此专栏以及详细思路和完全代码。希望有需求的小伙伴不要错过笔者精心打造的专栏。

上篇文章本来是打算完结神经网络的,忘记了写的是基于梯度的反向传播的计算,并不是基于激活函数误差的反向传播的神经网络。对于数据微分来说,它的计算非常消耗时间,会导致epoch迭代数据传播效率低下,自然导致训练准确率低。如果对误差反向传播较为熟悉的话,就没有必要用数值微分,故掌握误差反向传播需要掌握的比较熟练。

我们仍然从基础原理一步一步来理解反向传播的计算方法,这样一来基础比较扎实且容易明白。
一、ReLU反向传播实现
激活函数我们有对ReLU基本了解:
ReLU(Rectified Linear Activation)函数是深度学习中常用的非线性激活函数之一。它在神经网络中广泛应用,因为它简单有效,能够解决梯度消失问题,并且在实际应用中取得了良好的结果。
ReLU 函数的定义很简单:对于任何输入值 x,输出等于输入 x(如果 x 大于等于零),或者输出为零(如果 x 小于零)。数学表达式如下:

也就是说如果前向传播的输入大于0,则直接传给下一层;如果为0则直接传给下一层。
通过上述描述,我们可以求出y关于x的导数:
那么ReLU的反向传播为的实现代码为:
class Relu:def __init__(self):self.x=Nonedef forward(self,x):self.x = np.maximum(0,x)out = self.xreturn outdef backward(self,dout):dx = doutdx[self.x <= 0]=0return dx是不是比较好理解,方向传播即为原计算方程进行偏导,那么我们再来看看Sigmoid的反向传播。
二、Sigmoid反向传播
Sigmoid函数公式我们知道为:
,通常用于二元分类模型。
这里推荐一本书能够更加系统基础的学习神经网络:深度学习与图像识别:原理与实践
里面有很详细的推导过程,这里借用书上Sigmoid计算图来展示:

那么对于反向传播我们需要反着来推,从右向左依次来看:
- 对
进行求偏导,不知道大家大学高数学得怎么样了,对其求偏导为
- 第二步进行反响传播时,会将上游的值
乘以本阶段的导数,对于
求导得到的导数为
,故第二步的导数为
- 第三步
求导自然是-1.故最终求导为
,之后乘以上层求导结果,输出为
.
最后我们Python实现一下:
class _sigmoid:def __init__(self):self.out = Nonedef forward(self,x):out = 1/(1+np.exp(-x))self.out=outreturn outdef backward(self,dout):dx = dout*self.out*(1-self.out)return dx三、Affine层
神经网络中的 Affine 层(也称为全连接层或线性层)在神经网络中扮演着重要的角色,其主要作用是引入线性变换和权重参数。这一层在前馈神经网络中用于将输入数据与权重相乘,然后加上偏置,从而产生输出。
Affine通常被加在卷积神经网络或循环神经网络中作为最终预测前的输出的顶层。一般形式为:
,其中x是层输入,w是参数,b是一个偏置量,f是一个非线性激活函数。
这里需要注意的是X基本为多个,也就是矩阵。如果加上1偏置量的话,偏置量会被加到各个X-W中去。
class Affine:def __init__(self,W,b):self.W=Wself.b=bself.x=Noneself.dW=Noneself.db=Nonedef forward(self,x):self.x=xout=np.dot(x,self.W)+self.breturn outdef backward(self,dout):dx = np.dot(dout,self.W.T)self.dW = np.dot(self.x.T,dout)self.db = np.sum(dout,axis=0)return dx四、基于数值微分和误差反向传播的比较
我们现在接触了两种梯度计算的方法:一种是基于数值微分的方法,另一种是基于误差反向传播的方法,对于数值微分来说,计算消耗是比较大的,用时很长。所以一般都是推荐使用误差反向传播,具体代码如下:
from collections import OrderedDict
import numpy as np
class TwoLayerNet:def __init__(self,input_size,hidden_size,output_size,weight_init_std = 0.01):#权重self.params = {}self.params['W1'] = weight_init_std * np.random.randn(input_size,hidden_size)self.params['b1'] = np.zeros(hidden_size)self.params['W2'] = weight_init_std * np.random.randn(hidden_size,output_size)self.params['b2'] = np.zeros(output_size)#生成层self.layers = OrderedDict()self.layers['Affine1'] = Affine(self.params['W1'],self.params['b1'])self.layers['Relu1'] = Relu()self.layers['Affine2'] = Affine(self.params['W2'],self.params['b2'])self.layers['Relu2'] = Relu()self.lastLayer = SoftmaxWithLoss()def predict(self,x):for layer in self.layers.values():x = layer.forward(x)return x#x:输入数据,y:监督数据def loss(self,x,y):p = self.predict(x)return self.lastLayer.forward(p,y)def accuracy(self,x,y):p = self.predict(x)p = np.argmax(y,axis=1)if y.ndim != 1:y = npp.argmax(y,axis=1)accuracy = np.sum(p==y)/float(x.shape[0])return accuracy#x:输入数据,y:监督数据def numerical_gradient(self,x,y):loss_W = lambda W: self.loss(x,y)grads = {}grads['W1'] = numerical_gradient(loss_W, self.params['W1'])grads['b1'] = numerical_gradient(loss_W, self.params['b1'])grads['W2'] = numerical_gradient(loss_W, self.params['W2'])grads['b2'] = numerical_gradient(loss_W, self.params['b2'])return gradsdef gradient(self , x, y):#forwardself.loss(x,y)#backwarddout = 1dout = self.lastLayer.backward(dout)layers = list(self.layers.values())layers.reverse()for layer in layers:dout = layer.backward(dout)#设定grads = {}grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].dbgrads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].dbreturn gradsnetwork = TwoLayerNet(input_size = 784,hidden_size = 50 , output_size = 10)
x_batch = x_train[:100]
y_batch = y_train[:100]
grad_numerical = network.numerical_gradient(x_batch,y_batch)
grad_backprop = network.gradient(x_batch,y_batch)for key in grad_numerical.keys():diff = np.average(np.abs(grad_backprop[key]-grad_numerical[key]))print(key+":"+str(diff))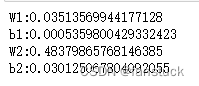
两者差值并不是很大,那么我们再看看准确率:
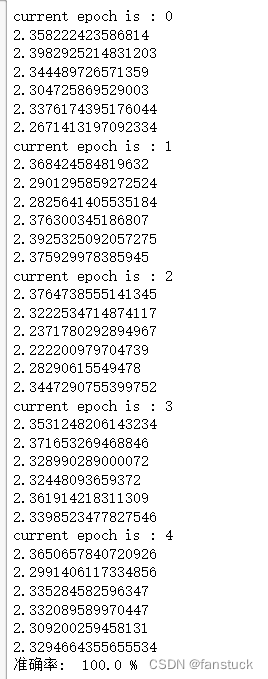
是不是感觉很厉害了,那么到这里神经网络基础内容就结束了,我们完成了从输入层-前向传播-权重偏置-激活函数-反向传播-前向传播----....网络的计算框架搭建,基本内容已经掌握了。那么我们现在可以开启深度学习网络的深入研究了,敬请期待下篇文章内容。
相关文章:

一文速学-让神经网络不再神秘,一天速学神经网络基础(七)-基于误差的反向传播
前言 思索了很久到底要不要出深度学习内容,毕竟在数学建模专栏里边的机器学习内容还有一大半算法没有更新,很多坑都没有填满,而且现在深度学习的文章和学习课程都十分的多,我考虑了很久决定还是得出神经网络系列文章,…...

C++ 异常处理——学习记录007
1. 概念 程序中的错误分为编译时错误和运行时错误。编译时出现的错误包括关键字拼写出错、语句分号缺少、括号不匹配等,编译时的错误容易解决。运行时出现的错误包括无法打开文件、数组越界和无法实现指定的操作。运行时出现的错误称为异常,对异常的处理…...

【BIM+GIS】“BIM+”是什么? “BIM+”技术详解
对于我们日常生活影响最大的是信息化和网络化给我们的日常生活带来革命性的变化。“互联网+“在建筑行业里可以称为“BIM+”。“BIM+”"即是通过BIM与各类技术(互联网、大数据等)结合去完成不同的任务。将产品的全生命周期和全制造流程的数字化以及基于信息通信技术的模块…...

Flink算子如何限流
目录 使用方法 调用类图 内部源码 GuavaFlinkConnectorRateLimiter RateLimiter 使用方法 重写AbstractRichFunction中的open()方法,在处理数据前调用limiter.acquire(1); 调用limiter.open(getRuntimeContext())的源码,实际内部是RateLimiter,根据并行度算出subTask…...

垃圾分代收集的过程是怎样的?
垃圾分代收集是Java虚拟机(JVM)中一种常用的垃圾回收策略。该策略将堆内存分为不同的代(Generation),通常分为年轻代(Young Generation)和老年代(Old Generation)。不同代的对象具有不同的生命周期和回收频率。 下面是Java中垃圾分代收集的一般过程: 1…...
NPM 常用命令(四)
目录 1、npm diff 1.1 描述 1.2 过滤文件 1.3 配置 diff diff-name-only diff-unified diff-ignore-all-space diff-no-prefix diff-src-prefix diff-dst-prefix diff-text global tag workspace workspaces include-workspace-root 2、npm dist-tag 2.1 常…...
Anaconda虚拟环境下导入opencv
文章目录 解决方法测试 解决方法 1、根据自己虚拟环境对于的python版本与电脑对应的位长选择具体的版本,例如python3.9选择cp39,64位电脑选择64 下载地址:资源地址 若是不确定自己虚拟环境对应的python版本,可以输入下列命令&…...
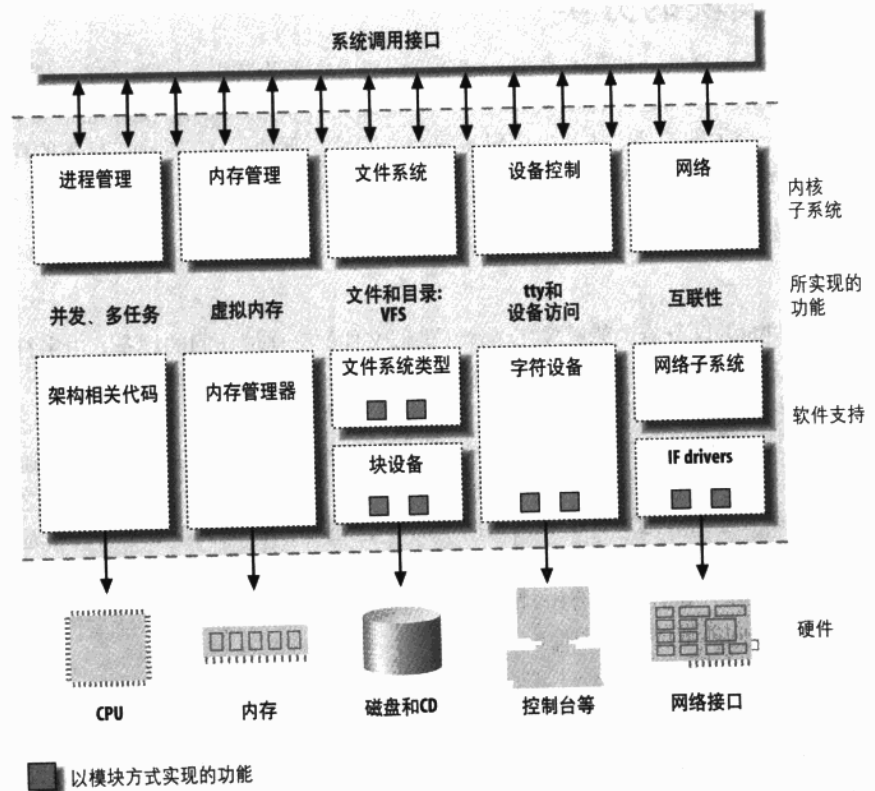
Linux设备驱动程序
一、设备驱动程序简介 图1.1 内核功能的划分 可装载模块 Linux有一个很好的特性:内核提供的特性可在运行时进行扩展。这意味着当系统启动 并运行时,我们可以向内核添加功能( 当然也可以移除功能)。 可在运行时添加到内核中的代码被称为“模块”。Linux内核支持好几…...

mybatis <if>标签判断“0“不生效
原if标签写法 <if test"type 0"><!--内部逻辑--> </if> 这种情况不生效,原因是mybatis是用OGNL表达式来解析的,在OGNL的表达式中,0’会被解析成字符(而我传入的type却是string),java是强类型的,cha…...

企业数据的存储形式与方案选择
企业数据的存储形式 DAS(直接附加存储):企业初期银行规模不大,企业的数据存储需求也比较简单,因此对企业数据存储的要求就是安全保存并可以随时调用。而DAS的之间连接可以解决单台服务器的存储空间扩展,高…...
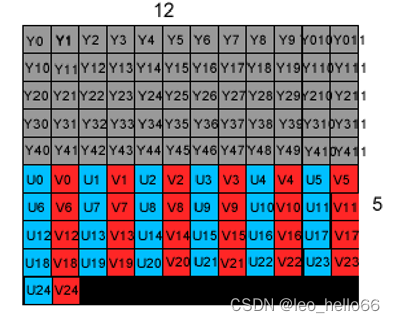
图像处理简介
目录 基本术语 1 .图像(image) 1.1 像素(Pixel) 1.2 颜色深度(Color Depth) 1.3 分辨率(Resolution) 1.4 像素宽高比(Pixel Aspect Ratio) 1.5 帧率(FPS) 1.6 码率(BR) 1. …...
 doesn‘t match this client (41); killing.的解决办法)
adb server version (19045) doesn‘t match this client (41); killing.的解决办法
我是因为安装了360手机助手,导致adb版本冲突。卸载之后问题解决 根据这个思路,如果产生"adb server version (19045) doesn’t match this client (41); killing."的错误,检查一下是否有多个版本的adb服务。...
实验室的服务器和本地pycharm怎么做图传
提前说一个 自认为 比较重要的一点: 容器中安装opencv,可以先试试用 apt install libopencv-dev python3-opencv 我感觉在图传的时候用的不是 opencv-python 而是ubuntu的opencv库 所以用 apt install 安装试一下 参考 远程调试 qt.qpa.xcb: coul…...

Vue + Element UI 前端篇(五):国际化实现
Vue Element UI 实现权限管理系统 前端篇(五):国际化实现 国际化支持 1.安装依赖 执行以下命令,安装 i18n 依赖。 yarn add vue-i18n $ yarn add vue-i18n yarn add v1.9.4 warning package-lock.json found. Your project …...
[ROS]虚拟机ubuntu18.04系统里面运行usb_cam
首先安装usb_cam sudo apt-get install ros-melodic-usb-cam 运行: roscore roslaunch usb_cam usb_cam-test.launch 如果一运行报错,首先确认是否存在/dev/video0 可以使用ls /dev/video*查看,如果没有就是没有连接摄像头,…...

常用通讯协议比较
dubbo与http1.0的区别 二进制协议:Dubbo使用自定义的二进制协议,而HTTP 1.0使用文本,发送一条相同的消息,http1.0会有更大的网络开销。 连接复用:Dubbo采用单一的多路复用NIO长链接,每个请求都有一个对应的…...

鼠标键盘管理 ShareMouse for Mac最新
软件“ShareMouse”允许您通过单个鼠标和键盘控制多台计算机: 将鼠标移动到您想要控制的计算机的监视器上,指针会神奇地跳转到该计算机。任何鼠标和键盘输入都会传输到相应的计算机。 与网络KVM类似,ShareMouse通过本地LAN传输鼠标移动和点…...
【ALM工具软件】上海道宁与Perforce为您带来用于整个生命周期的应用程序生命周期管理软件
Helix ALM是 用于整个生命周期的 应用程序生命周期管理的ALM软件 具有专用于 需求管理(Helix RM)、测试用例管理(Helix TCM) 问题管理(Helix IM)的功能模块 Helix ALM提供了 无与伦比的可追溯性 您将…...

Android图形-架构2
目录 引言 组件概述 底层组件: 上层组件: 引言 Android图形架构主要涉及些什么呢? 1)Android 系统级图形架构的基本元素? 2)应用框架和多媒体系统如何使用这些元素? 3)图形数据…...

文字验证码:简单有效的账号安全守卫!
前言 文字验证码不仅是一种简单易懂的验证方式,同时也是保护您的账号安全的重要工具。通过输入正确的文字组合,您可以有效地确认自己的身份,确保只有真正的用户才能访问您的账号。 HTML代码 <script src"https://cdn6.kgcaptcha.…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...

欢乐熊大话蓝牙知识17:多连接 BLE 怎么设计服务不会乱?分层思维来救场!
多连接 BLE 怎么设计服务不会乱?分层思维来救场! 作者按: 你是不是也遇到过 BLE 多连接时,调试现场像网吧“掉线风暴”? 温度传感器连上了,心率带丢了;一边 OTA 更新,一边通知卡壳。…...
OPENCV图形计算面积、弧长API讲解(1)
一.OPENCV图形面积、弧长计算的API介绍 之前我们已经把图形轮廓的检测、画框等功能讲解了一遍。那今天我们主要结合轮廓检测的API去计算图形的面积,这些面积可以是矩形、圆形等等。图形面积计算和弧长计算常用于车辆识别、桥梁识别等重要功能,常用的API…...

react-pdf(pdfjs-dist)如何兼容老浏览器(chrome 49)
之前都是使用react-pdf来渲染pdf文件,这次有个需求是要兼容xp环境,xp上chrome最高支持到49,虽然说iframe或者embed都可以实现预览pdf,但为了后续的定制化需求,还是需要使用js库来渲染。 chrome 49测试环境 能用的测试…...
