FPGA基本算术运算
FPGA基本算术运算
- FPGA基本算术运算
- 1 有符号数与无符号数
- 2 浮点数及定点数
- I、定点数的加减法
- II、定点数的乘除法
- 3 仿真验证
- i、加减法验证
- ii、乘除法验证
FPGA基本算术运算
FPGA相对于MCU有并行计算、算法效率较高等优势,但同样由于没有成型的FPU等MCU内含的浮点数运算模块,导致一些基本的符号数、浮点数运算需要我们自己进行管理。因此需要我们对基本的运算法则进行了解。基本类别如下,即:

1 有符号数与无符号数
无符号数即为没有符号的数,简单点就是全部为正数运算的数没有负数。有符号数字便是有正与负数的数。那么在同样位数的条件下,表示的有符号数范围更加少,如下。
reg [7:0] unsigned_a; //定义一个无符号8位数 //既然无符号,则可表示 0 - 0xFF,即 0 -255;//256 - 0x100 即超出了8位
以上是无符号数的概念,而有符号数则为了表示符号,将补码的概念引入了基本数体系,建立了符号数体系。
符号体系中,补码即将数分为符号位和基本数位;最高位表示符号位,1为负,0为正数,其他基本数位则表示正常数码。
reg signed [7:0] sign_b; //8位有符号数 bit7:符号位; bit6-bit0: 数位//此时数位,最大只能表示0-127,较8位无符号数可表示范围减少一半同时,为了方便运算减法,建立了补码运算体系,即a-b可转换为 a + b[补码]。
因此,定义,正数的原码、反码、补码均相同,负数原码、反码、补码经过以下运算得到:
//正数:8’d82 - 8'b0101_0010
//原码:8'b0101_0010
//反码:8'b0101_0010
//补码:8'b0101_0010//负数: -8’d82
//原码:8'b0101_0010
//反码:8'b1010_1101 (原码取反)
//补码:8'b1010_1110 (反码 + 1)//8位有符号数:
//正数: 8’d127 补码: 8'hff
//....
//正数: 8’d2 补码: 8'h02
//正数: 8’d1 补码: 8'h01
// 8'd0 补码: 8'd0
//负数: -8’d1 补码: 8'hff
//负数: -8’d2 补码: 8'hfe
// ...
//负数: -8’d127 补码: 8'h81
根据以上规则,发现0是个特殊的数字,+0的补码即是8‘h0,而-0的补码是8’h80,而0 仅仅就是0。于是一般规定,8’h80为-128。因此8位有符号数范围为[-128,127],相对于无符号数[0,255],数值大小降低了一半。
2 浮点数及定点数
浮点数主要是遵守 IEEE754 浮点数标准这里不再缀述。而定点数,即是固定小数点的一种方式,如
//十进制小数: 32.15 - 二进制:100000.00100110011001100110011001100110011001100110011
//保留10位二进制小数后 - 100000.0010011001 (32.1494140625) - 有截断误差
//定义定点数为Q10 - 即将原来的数乘以2^10 - 1000000010011001(32921)
//Qn 表示小数点在第几位前面
I、定点数的加减法
不同定点数的加减要转换为同一定点格式才能相加减,即
//32.15 - 32921(Q10)
//15.62 - 7997(Q9)
//32.15 + 15.62 = 47.77
// 32921 + 7997* 2^(10-9) = 48915(Q10)
// 48915/ 2^10 = 47.7685546875 [有截断误差]
Qm的定点数 +(-) Qn位的定点数{m>n},需要将n位数定点扩展到同一位置,然后进行运算,结果为Qm。
因此m位的定点数 +(-) n位的定点数,首先需要将结果变量扩展到m+1位(防止溢出)
II、定点数的乘除法
//32.15 - 32921(Q10)
//15.62 - 7997(Q9)
//32.15 * 15.62 = 502.183
// 32921 * 7997 = 263269237(Q19)
// 263269237/ 2^19 = 502.1462192535400390625 [有截断误差]
Qm的定点数 *(/) Qn位的定点数{m>n},结果为Q(m+n)。
因此m位的定点数 *(/) n位的定点数,首先需要将结果变量扩展到m+n位(防止溢出)
3 仿真验证
i、加减法验证
对如下module进行激励测试:
module add(input [7:0] a,input [7:0] b,output [7:0] c);wire [8:0] add_out;
wire [8:0] sub_out;wire [7:0] add_out_2;
wire [7:0] sub_out_2;assign add_out = a+b;
assign sub_out = a-b;assign add_out_2 = a+b;
assign sub_out_2 = a-b;endmodule
第一阶段,a->8’d12; a->8’d35。

可以看到8位及9位的结果输出均正常,这时12-35=-23的结果自动变为补码。
第二阶段,a->-8’d12; a->8’d35。

第二阶段这里就发现了9位的输出结果明显不对,这里0xf4(-12) + 0x23 = 0x117;结果溢出了。正常情况,有符号数符号位不会参与运算,这里参与了运算导致了错误[主要是结果溢出导致]。
有两种办法进行修改:
1)将input 改为:
input signed [7:0] a,
input signed [7:0] b,
2)将加法运算进行扩展后计算
assign add_out = {a[7],a} + {b[7],b}; //扩展符号位
assign sub_out = {a[7],a} - {b[7],b};
结论:对于是否定义有无符号数,即使是无符号数,运算产生负数后,也会使用补码进行表示。但是如果计算结果存在溢出,则会产生错误,所以即使不使用signed类型也可,但需要注意位宽。
ii、乘除法验证
module chengc(input [7:0] c1,input [7:0] c2,output [7:0] d2);wire [15:0] mux_out;
wire [15:0] divid_out;wire [7:0] mux_out_2;
wire [7:0] divid_out_2;assign mux_out = c1 * c2;
assign divid_out = c1 / c2;assign mux_out_2 = c1 * c2;
assign divid_out_2 = c1 / c2;endmodule
与加减法相似,在溢出时,仍旧出现了符号位参与运算导致的错误。

这个时候进行如下修改:
module chengc(input signed [7:0] c1,input signed [7:0] c2,output [7:0] d2);wire signed [15:0] mux_out;
wire signed [15:0] divid_out;wire [15:0] mux_out_2;
wire [15:0] divid_out_2;assign mux_out = ({ {8{c1[7]}},c1}) * ( { {8{c2[7]}}, c2});
assign divid_out = ({ {8{c1[7]}},c1}) / ( { {8{c2[7]}}, c2});assign mux_out_2 = c1 * c2;
assign divid_out_2 = c1 / c2;endmodule
此时输出结果如下:

在除法运算中,符号位仍旧参与了运算,导致结果失常。因此这里并不推荐直接使用 * / ,FPGA最好使用片上自带的DSP模块进行运算,也可使用移位及加减进行近似运算。如:
//a * 0.625 = a * (0.10011101011100001010001111010111000010100011110101111)b//a * 1/2 + a*1/8 + a*1/16 + a*1/32 + ... +.. 进行近似运算定点数乘除法,因已将定点数转为了整数,因此也可参考该过程。
相关文章:

FPGA基本算术运算
FPGA基本算术运算 FPGA基本算术运算1 有符号数与无符号数2 浮点数及定点数I、定点数的加减法II、定点数的乘除法 3 仿真验证i、加减法验证ii、乘除法验证 FPGA基本算术运算 FPGA相对于MCU有并行计算、算法效率较高等优势,但同样由于没有成型的FPU等MCU内含的浮点数运…...
Linux Input子系统
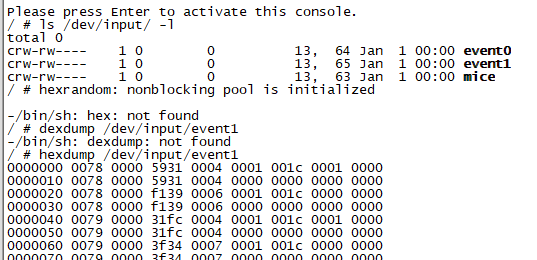
一、基本概念 按键、鼠标、键盘、触摸屏等都属于输入(input)设备,Linux 内核为此专门做了一个叫做 input子系统的框架来处理输入事件。本质属于字符设备。 1. input子系统结构如下: input 子系统分为 input 驱动层、input 核心层、input 事件处理层&…...
commet与websocket
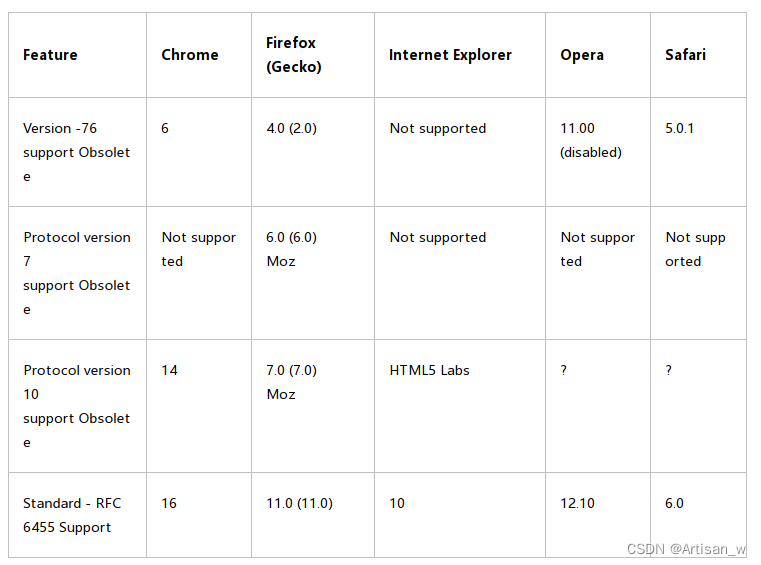
commet与websocket Comet 前言 Comet是一种用于web的技术,能使服务器能实时地将更新的信息传送到客户端,而无须客户端发出请求,目前有两种实现方式,长轮询和iframe流。 实现方式 长轮询 长轮询是在打开一条连接以后保持&…...
python3 简易 http server:实现本地与远程服务器传大文件
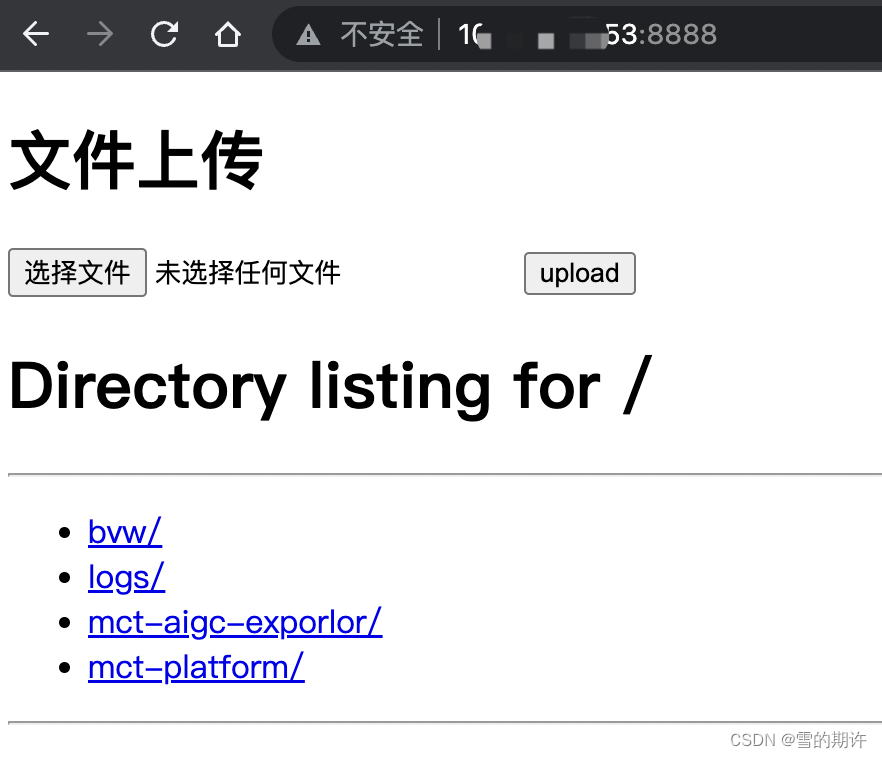
在个人目录下创建新文件httpserver.py : vim httpserver.py文件内容为python3代码: # !/usr/bin/env python3 import datetime import email import html import http.server import io import mimetypes import os import posixpath import re import…...
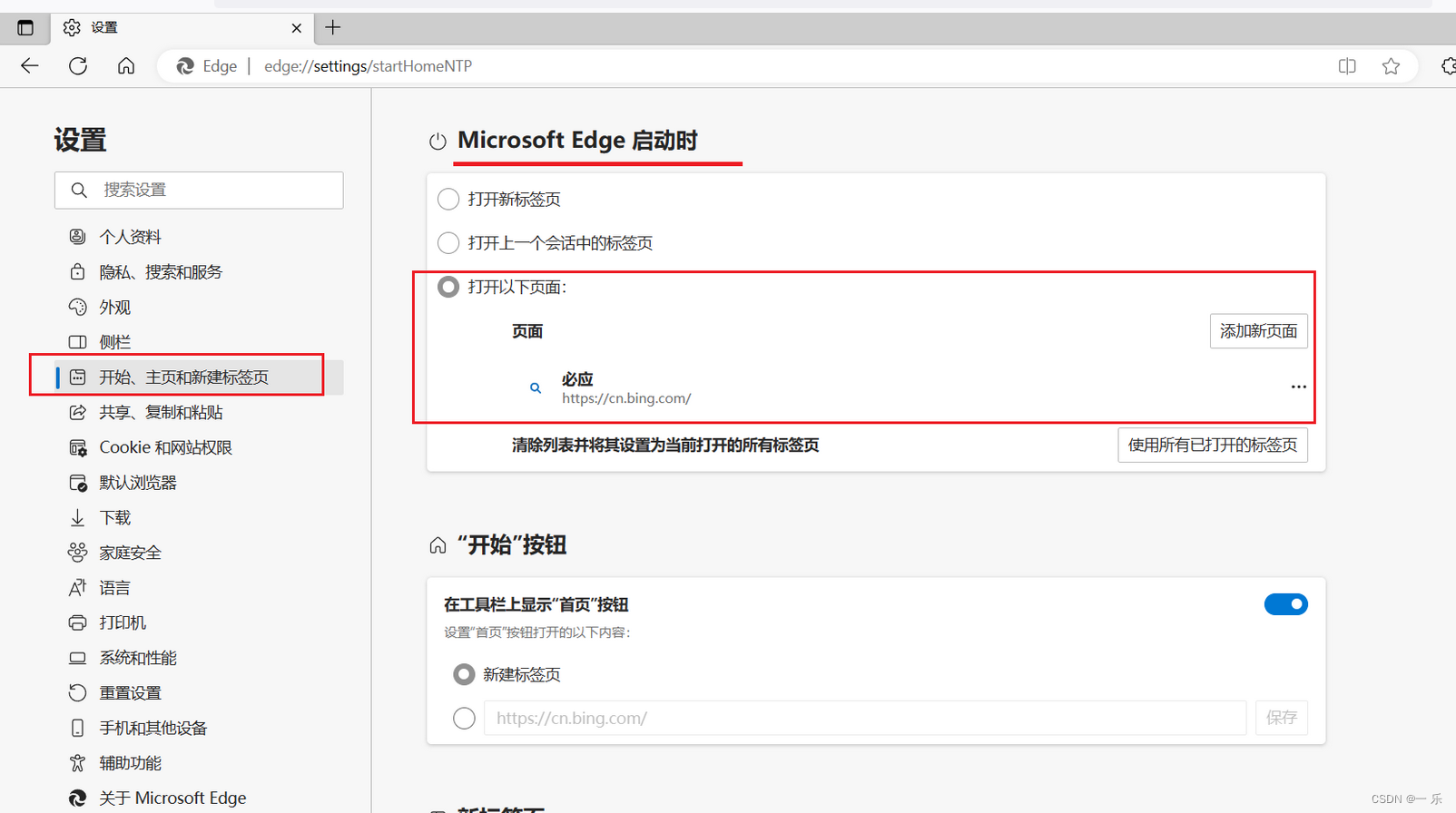
Microsoft Edge 主页启动diy以及常用的扩展、收藏夹的网站
一、Microsoft Edge 主页启动diy 二、常用的扩展 1、去广告:uBlock Origin 2、翻译: 页面翻译:右键就有了,已经内置了划词翻译 3、超级复制 三、收藏夹的网站...

文末送书!谈谈原型模式在JAVA实战开发中的应用(附源码+面试题)
作者主页:Designer 小郑 作者简介:3年JAVA全栈开发经验,专注JAVA技术、系统定制、远程指导,致力于企业数字化转型,CSDN博客专家,蓝桥云课认证讲师。 本文讲解了 Java 设计模式中的原型模式,并给…...

视频汇聚/视频云存储/视频监控管理平台EasyCVR启动时打印starting server:listen tcp,该如何解决?
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,可实现视频监控直播、视频轮播、视频录像、云存储、回放与检索、智能告警、服务器集群、语音对讲、云台控制、电子地图、H.265自动转码H.264、平台级联等。为了便于用户二次开发、调用与集成,…...
【Linux从入门到精通】通信 | 管道通信(匿名管道 命名管道)
本派你文章主要是对进程通信进行详解。主要内容是介绍 为什么通信、怎么进行通信。其中本篇文章主要讲解的是管道通信。希望本篇文章会对你有所帮助。 文章目录 一、进程通信简单介绍 1、1 什么是进程通信 1、2 为什么要进行通信 1、3 进程通信的方式 二、匿名管道 2、1 什么是…...

实践和项目:解决实际问题时,选择合适的数据结构和算法
文章目录 选择合适的数据结构数组链表栈队列树图哈希表 选择合适的算法实践和项目 🎉欢迎来到数据结构学习专栏~实践和项目:解决实际问题时,选择合适的数据结构和算法 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:IT…...
上线检查工具(待完善)
根据V11《CEBPM系统上线CheckList》整理而得,适用于V11,DHERP,Oracle和MSSQL数据库,检查内容还不完善。 上图: 1)数据库连接 2)双击[连接别名],可选择历史连接 3)主界面…...
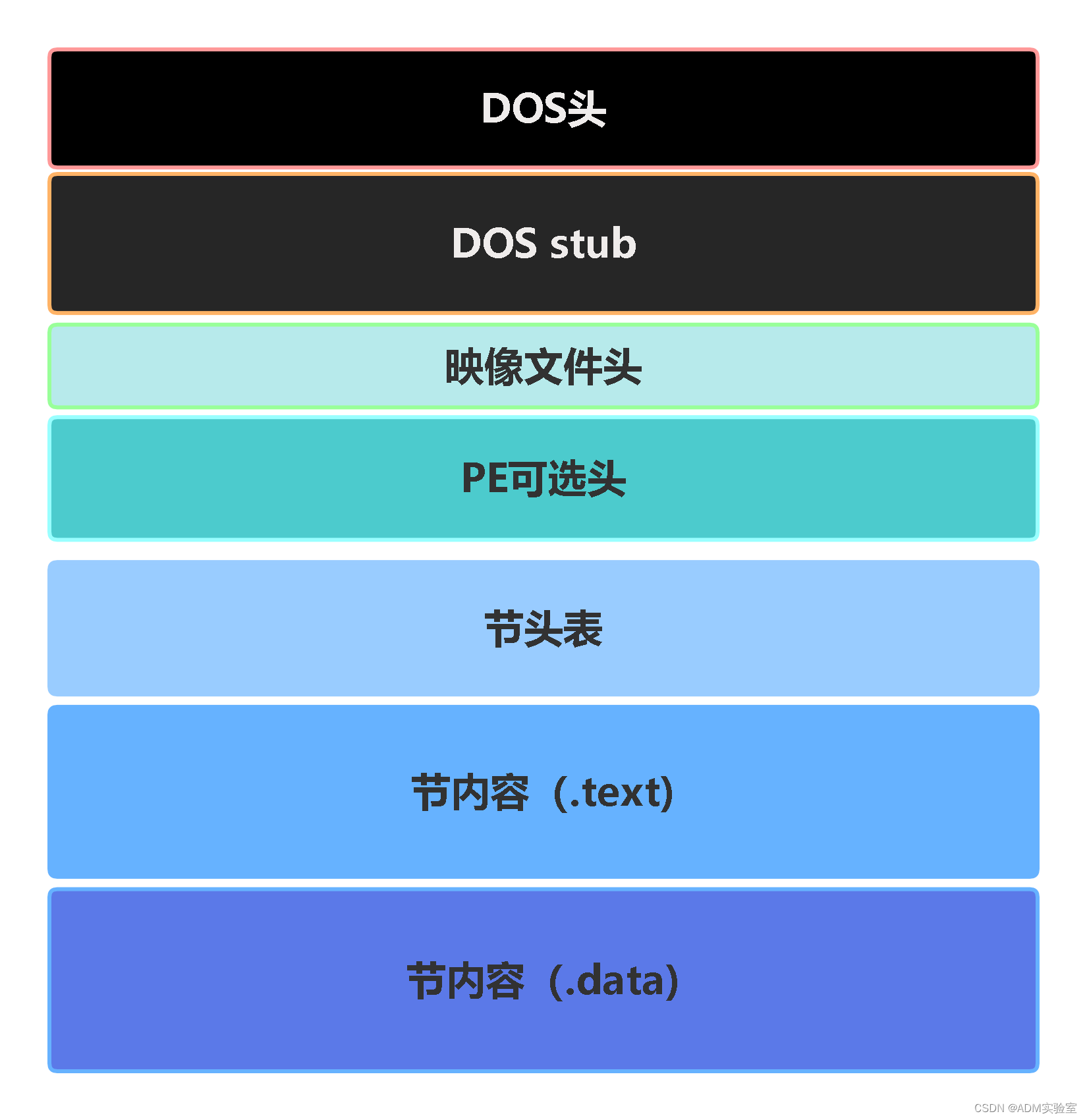
PE文件格式详解
摘要 本文描述了Windows系统的PE文件格式。 PE文件格式简介 PE(Portable Executable)文件格式是一种Windows操作系统下的可执行文件格式。PE文件格式是由Microsoft基于COFF(Common Object File Format)格式所定义的,…...

【Alibaba中间件技术系列】「RocketMQ技术专题」RocketMQ消息发送的全部流程和落盘原理分析
RocketMQ目前在国内应该是比较流行的MQ 了,目前本人也在公司的项目中进行使用和研究,借着这个机会,分析一下RocketMQ 发送一条消息到存储一条消息的过程,这样会对以后大家分析和研究RocketMQ相关的问题有一定的帮助。 分析的总体…...

关于vue首屏加载loading问题
注意:网上搜索出来的都是教你在index.html里面<div id"app"><div class"loading"></div>或者在app.vue Mounte生命周期函数控制app和loading的显示和隐藏,这里会有一个问题,就是js渲染页面需要时间,一…...

数据库性能测试实践:慢查询统计分析
01、慢查询 查看是否开启慢查询 mysql> show variables like %slow%’; 如图所示: 系统变量log_slow_admin_statements 表示是否将慢管理语句例如ANALYZE TABLE和ALTER TABLE等记入慢查询日志启用log_slow_extra系统变量 (从MySQL 8.0.14开始提供&a…...
)
windows wsl ssh 配置流程 Permission denied (publickey)
wsl ssh连接失败配置流程 1、wsl2 ifconfig的网络ip是虚拟的ip,所以采用wsl1 2、wsl1的安装教程。 3、openssh-server重装 sudo apt-get update sudo apt-get remove openssh-server sudo apt-get install openssh-server4、修改ssh配置文件 sudo vim /etc/ss…...

OpenCV(五):图像颜色空间转换
目录 1.图像颜色空间介绍 RGB 颜色空间 2.HSV 颜色空间 3.RGBA 颜色空间 2.图像数据类型间的互相转换convertTo() 3.不同颜色空间互相转换cvtColor() 4.Android JNI demo 1.图像颜色空间介绍 RGB 颜色空间 RGB 颜色空间是最常见的颜色表示方式之一,其中 R、…...

一图胜千言!数据可视化多维讲解(Python)
数据聚合、汇总和可视化是支撑数据分析领域的三大支柱。长久以来,数据可视化都是一个强有力的工具,被业界广泛使用,却受限于 2 维。在本文中,作者将探索一些有效的多维数据可视化策略(范围从 1 维到 6 维)。…...

Hbase相关总结
Hbase 1、Hbase的数据写入流程 由客户端发起写入数据的请求, 首先会先连接zookeeper 从zookeeper中获取到当前HMaster的信息,并与HMaster建立连接从HMaster中获取RegionServer列表信息 连接meta表对应的RegionServer地址, 从meta表获取当前要写入的表对应region被那个RegionS…...

C++ Primer Plus第二章编程练习答案
答案仅供参考,实际运行效果取决于运行平台和运行软件 1.编写一个C程序,它显示您的姓名和地址。 #include <iostream> using namespace std;int main() {cout << "My name is sakuraaa0908 C Primer Plus." << endl;cout &…...
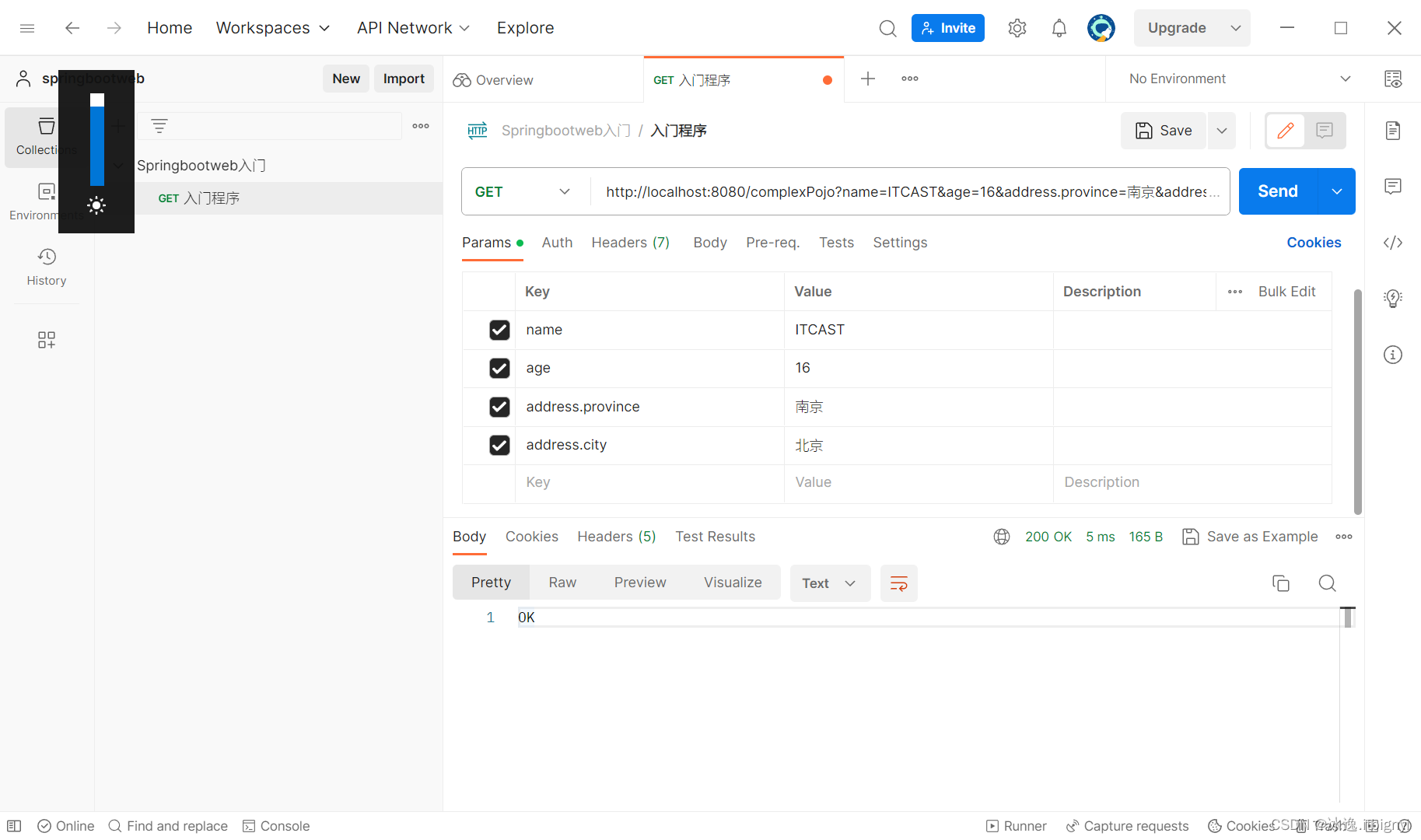
Web后端开发(请求响应)上
请求响应的概述 浏览器(请求)<--------------------------(HTTP协议)---------------------->(响应)Web服务器 请求:获取请求数据 响应:设置响应数据 BS架构:浏览器/服务器架构模式。…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

node.js的初步学习
那什么是node.js呢? 和JavaScript又是什么关系呢? node.js 提供了 JavaScript的运行环境。当JavaScript作为后端开发语言来说, 需要在node.js的环境上进行当JavaScript作为前端开发语言来说,需要在浏览器的环境上进行 Node.js 可…...

Linux基础开发工具——vim工具
文章目录 vim工具什么是vimvim的多模式和使用vim的基础模式vim的三种基础模式三种模式的初步了解 常用模式的详细讲解插入模式命令模式模式转化光标的移动文本的编辑 底行模式替换模式视图模式总结 使用vim的小技巧vim的配置(了解) vim工具 本文章仍然是继续讲解Linux系统下的…...
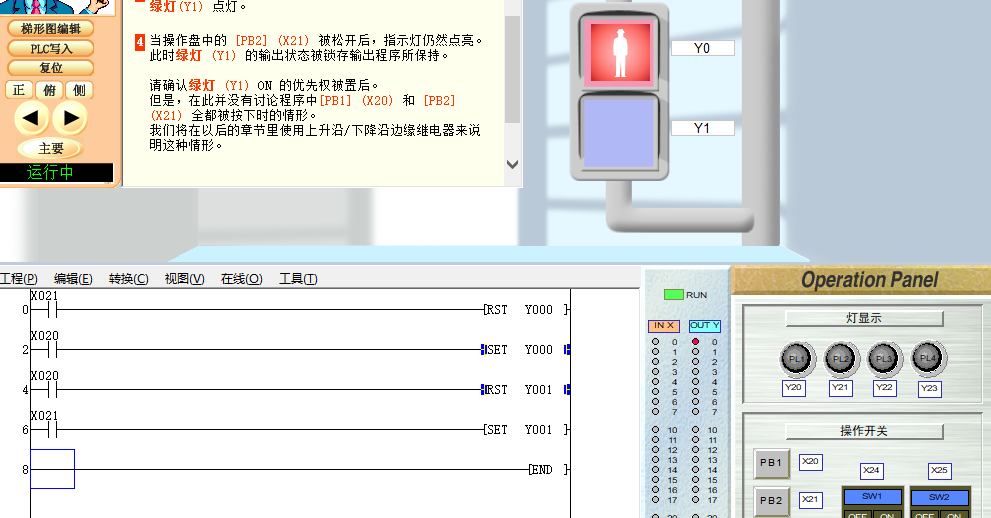
PLC入门【4】基本指令2(SET RST)
04 基本指令2 PLC编程第四课基本指令(2) 1、运用上接课所学的基本指令完成个简单的实例编程。 2、学习SET--置位指令 3、RST--复位指令 打开软件(FX-TRN-BEG-C),从 文件 - 主画面,“B: 让我们学习基本的”- “B-3.控制优先程序”。 点击“梯形图编辑”…...

JS面试常见问题——数据类型篇
这几周在进行系统的复习,这一篇来说一下自己复习的JS数据结构的常见面试题中比较重要的一部分 文章目录 一、JavaScript有哪些数据类型二、数据类型检测的方法1. typeof2. instanceof3. constructor4. Object.prototype.toString.call()5. type null会被判断为Obje…...
