类欧几里得算法
求 ∑ i = 0 n ⌊ a i + b c ⌋ \sum\limits_{i=0}^{n}\lfloor \frac{ai+b}{c} \rfloor i=0∑n⌊cai+b⌋
推式子步骤:
分类讨论
a = 0 a=0 a=0
是个最简式子
b ≥ c b\ge c b≥c 或 a ≥ c a\ge c a≥c
由 f ( a m o d c , b m o d c , c , n ) f(a\bmod c,b\bmod c,c,n) f(amodc,bmodc,c,n) 转移过来,拆一下括号就行
其他情况
设 M = ⌊ a n + b c ⌋ M=\lfloor\frac{an+b}{c}\rfloor M=⌊can+b⌋
⌊ a i + b c ⌋ = ∑ j = 1 M [ j ≤ ⌊ a i + b c ⌋ ] \lfloor \frac{ai+b}{c} \rfloor=\sum_{j=1}^M [j\le\lfloor\frac{ai+b}{c}\rfloor] ⌊cai+b⌋=∑j=1M[j≤⌊cai+b⌋]
- 拆一下后面的除号
- 把所有 j j j 变成 j − 1 j-1 j−1
- 交换求和顺序
- 变成 i > x i>x i>x 的形式
- 变成 n − i ≤ x n-i\le x n−i≤x 的形式
- 后面直接换成 f ( c , c − b − 1 , a , m − 1 ) f(c,c-b-1,a,m-1) f(c,c−b−1,a,m−1)
int floor_sum(int n, int c, int a, int b) {if(a==0) return (n+1)*(b/c); if(a>=c || b>=c) return floor_sum(n, c, a%c, b%c)+n*(n+1)/2*(a/c)+(n+1)*(b/c); int m=(a*n+b)/c; return n*m-floor_sum(m-1, a, c, c-b-1);
}
对于 ∑ i = 0 n ⌊ a i + b c ⌋ 2 , ∑ i = 0 n i ⌊ a i + b c ⌋ \sum\limits_{i=0}^{n}{\lfloor \frac{ai+b}{c} \rfloor}^2\,,\ \sum\limits_{i=0}^{n}i\lfloor \frac{ai+b}{c} \rfloor i=0∑n⌊cai+b⌋2, i=0∑ni⌊cai+b⌋ 的求解
推的方法类似,不过会互相调用
node floor_sum(int a, int b, int c, int n) {if(a==0) return {(n+1)*(b/c)%p, (n+1)*(b/c)%p*(b/c)%p, n*(n+1)%p*i2%p*(b/c)%p}; if(a>=c || b>=c) {node t=floor_sum(a%c, b%c, c, n); int F=t.f+n*(n+1)%p*i2%p*(a/c)%p+(n+1)*(b/c)%p; int G=t.g+2*t.h%p*(a/c)%p+2*(b/c)%p*t.f%p+n*(n+1)%p*(2*n+1)%p*i6%p*(a/c)%p*(a/c)%p+(n+1)*n%p*(a/c)%p*(b/c)%p+(n+1)*(b/c)%p*(b/c)%p; int H=t.h+n*(n+1)%p*(2*n+1)%p*i6%p*(a/c)%p+n*(n+1)%p*i2%p*(b/c)%p; return {F%p, G%p, H%p}; }int m=(a*n+b)/c; node t=floor_sum(c, c-b-1, a, m-1); int F=n*m%p-t.f; int G=n*m%p*(m+1)%p-2*t.f%p-2*t.h%p-F; int H=(m*n%p*(n+1)%p-t.g-t.f)%p*i2%p; return {F%p, G%p, H%p};
}相关文章:

类欧几里得算法
求 ∑ i 0 n ⌊ a i b c ⌋ \sum\limits_{i0}^{n}\lfloor \frac{aib}{c} \rfloor i0∑n⌊caib⌋ 推式子步骤: 分类讨论 a 0 a0 a0 是个最简式子 b ≥ c b\ge c b≥c 或 a ≥ c a\ge c a≥c 由 f ( a m o d c , b m o d c , c , n ) f(a\bmod c,b\bmod…...

c++读取和存储文件,对文件操作
#include<bits/stdc.h> using namespace std; int aa[100];//全局变量数组,用来接收我们从文件中读取的数据。 void zhuanhua(string a){//这个函数的作用是转化我们读取的数字,由于我们读取文件时//是按行读取,就是一下读取一行&…...

InfluxDB API -- InfluxDB笔记四
1.调试工具的安装 ApiPost (类似Postman) 2.InfluxDB v2 API 地址 官方地址: InfluxDB v2 API | InfluxDB OSS 2.7 Documentation 本地文档地址:host1:8086/docs 3.token认证 在web UI 的Load Data -> API Tokens里面可以复制,这个页面也可以创…...
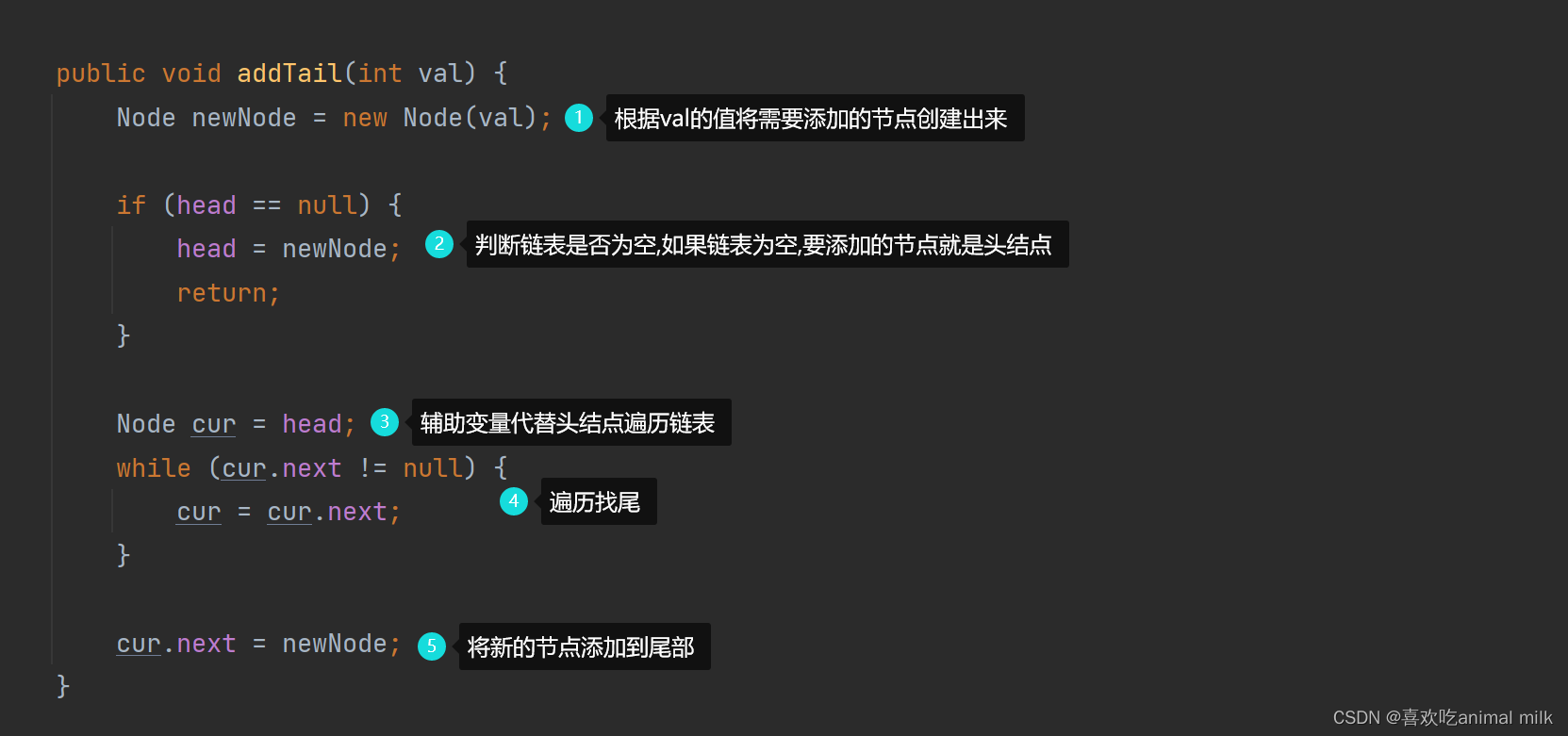
数据结构 - 单链表
文章目录 目录 文章目录 一、什么是链表? 线性表: 顺序表: 二、链表的分类和实现 分类: 实现: 1.创建节点类 2.创建单链表 1.addTail(尾增) 2.删除节点值为key的第一个节点 3.插入节点(在指定位置) 4.获取链表长度 总结 前言 大家好,这篇博客给大家讲一下什么是…...

化繁为简 面板式空调网关亮相上海智能家居展 智哪儿专访青岛中弘赵哲海
面对中央空调协议不开放和智能家居协议不统一的问题,青岛中弘选择中央空调控制器这一细分赛道入局智能家居市场,始终贯彻“所有空调,一个网关”的产品技术理念,逐渐探索出一条中弘的发展路径和商业模式。 在2023年的SSHT上海国际智…...
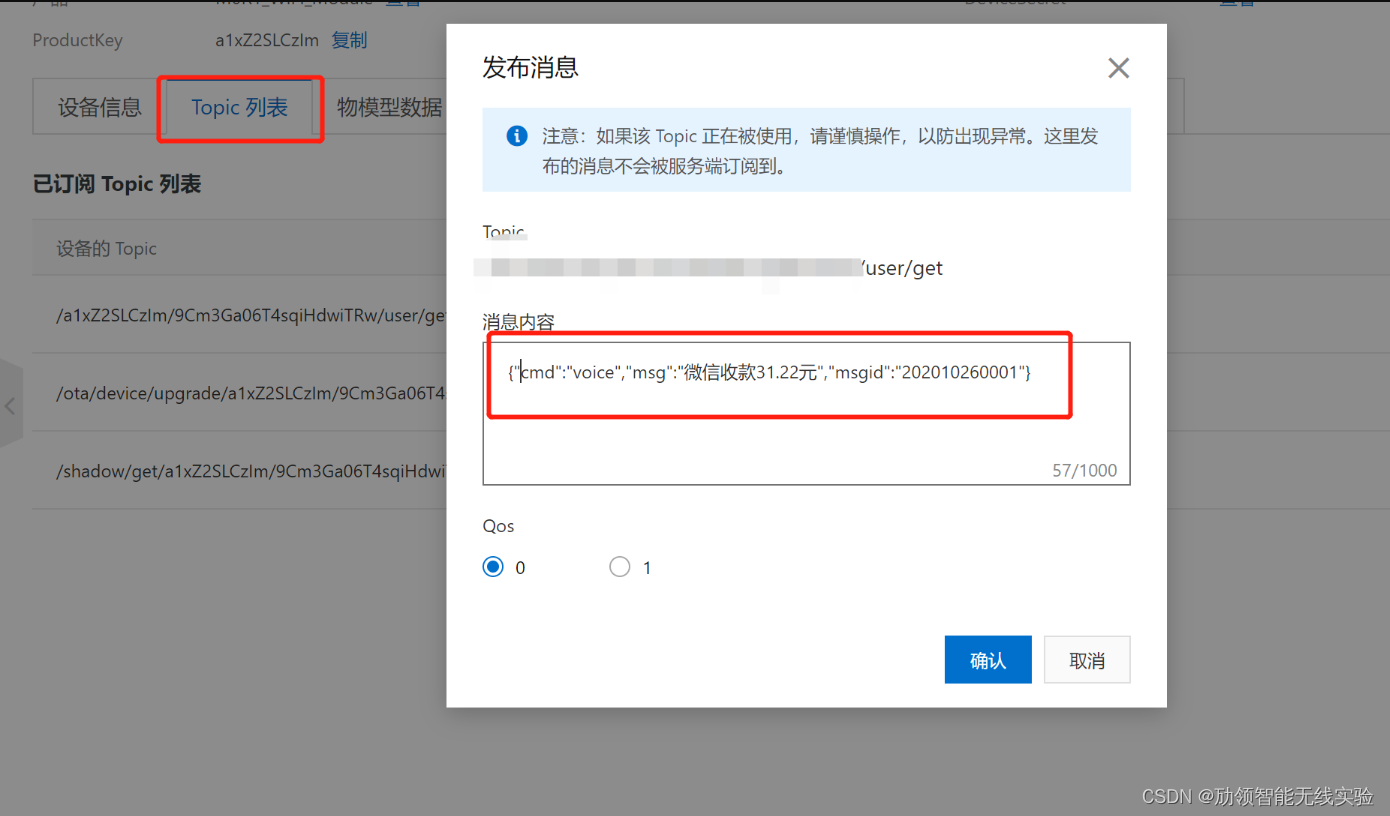
4G版本云音响设置教程阿里云平台版本
4G版本云音响设置教程介绍 第一章 介绍了在阿里云物联网平台生一个设备使用的三元素 第二章 转换阿里云三元素 为MQTT参数,并下载到设备中 第三章 阿里云物联网套件协议使用说明,如何发送数据至设备并播放 本文目录引导 目录 4G版本云音响设置教程介…...
STM32纯中断方式发送接收数据(串行通信;keil arm5;)
除了main文件其他文件均无修改,正常运行--在keil arm5内...
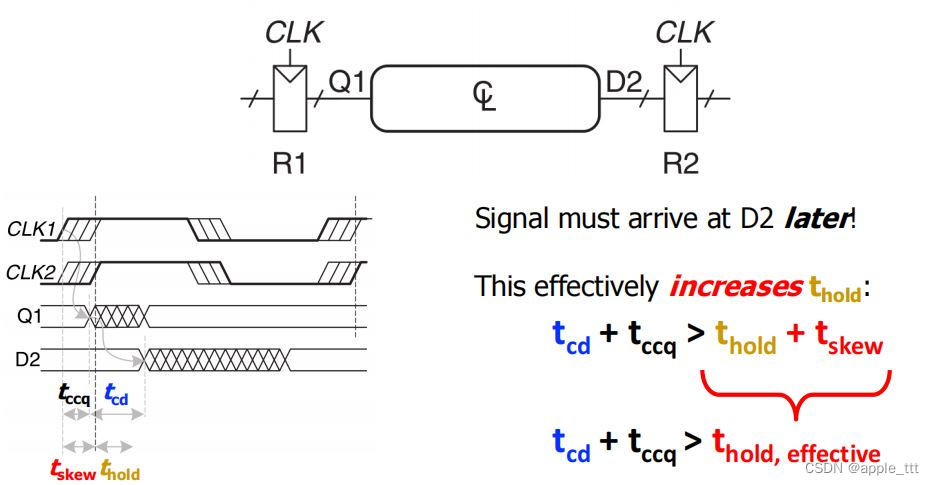
FPGA时序分析与约束(3)——时钟不确定性
一、前言 在之前的文章中,我们介绍了组合电路的时序和时序电路的时序问题,在阅读本文章之前,强烈推荐先阅读完本系列之前的文章,因为这是我们继续学习的理论的理论基础,前文链接: FPGA时序分析与约束&…...

【Java-HDFS】使用Java操作HDFS获取HDFS指定目录下的数据量大小
Maven依赖 <dependencies><dependency><groupId>junit</groupId><artifactId>junit</artifactId><version>RELEASE</version></dependency><dependency><groupId>org.apache.logging.log4j</groupId>…...
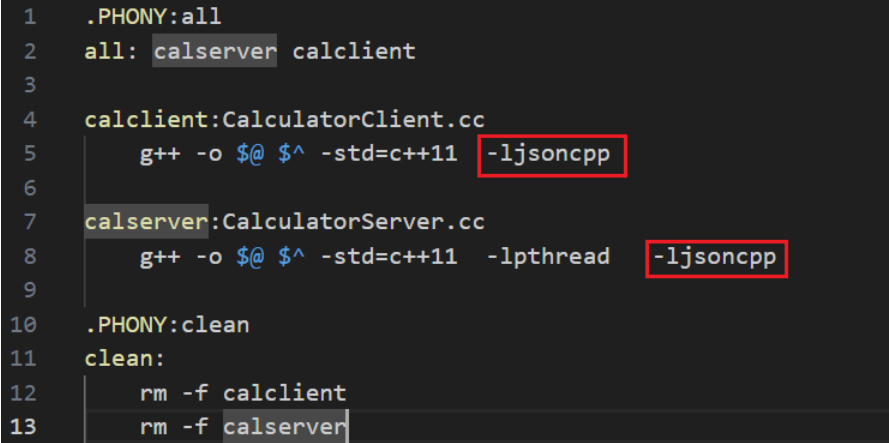
协议定制 + Json序列化反序列化
文章目录 协议定制 Json序列化反序列化1. 再谈 "协议"1.1 结构化数据1.2 序列化和反序列化 2. 网络版计算器2.1 服务端2.2 协议定制(1) 网络发送和读取的正确理解(2) 协议定制的问题 2.3 客户端2.4 代码 3. Json实现序列化反序列化3.1 简单介绍3.2 使用 协议定制 J…...
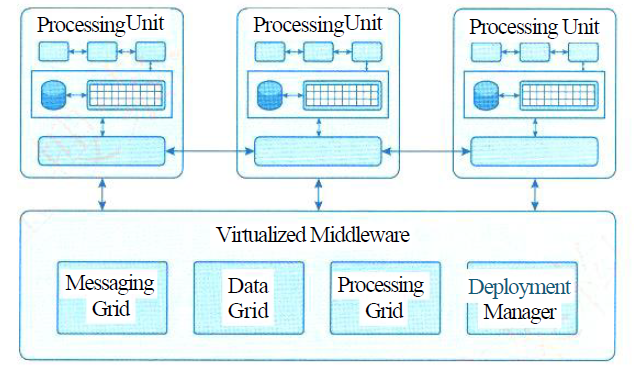
系统架构设计师(第二版)学习笔记----系统架构概述
【原文链接】系统架构设计师(第二版)学习笔记----系统架构概述 文章目录 一、系统架构的定义与发展历程1.1 架构的定义1.2 架构设计的作用1.3 架构设计产生的背景1.4 软件架构的发展历程1.5 模块化开发方法1.6 模块法方法分解模块遵循的原则1.7 软件工程…...

FPGA基本算术运算
FPGA基本算术运算 FPGA基本算术运算1 有符号数与无符号数2 浮点数及定点数I、定点数的加减法II、定点数的乘除法 3 仿真验证i、加减法验证ii、乘除法验证 FPGA基本算术运算 FPGA相对于MCU有并行计算、算法效率较高等优势,但同样由于没有成型的FPU等MCU内含的浮点数运…...
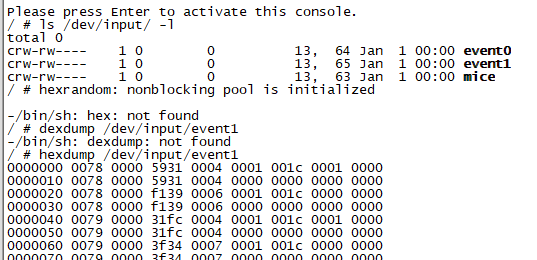
Linux Input子系统
一、基本概念 按键、鼠标、键盘、触摸屏等都属于输入(input)设备,Linux 内核为此专门做了一个叫做 input子系统的框架来处理输入事件。本质属于字符设备。 1. input子系统结构如下: input 子系统分为 input 驱动层、input 核心层、input 事件处理层&…...
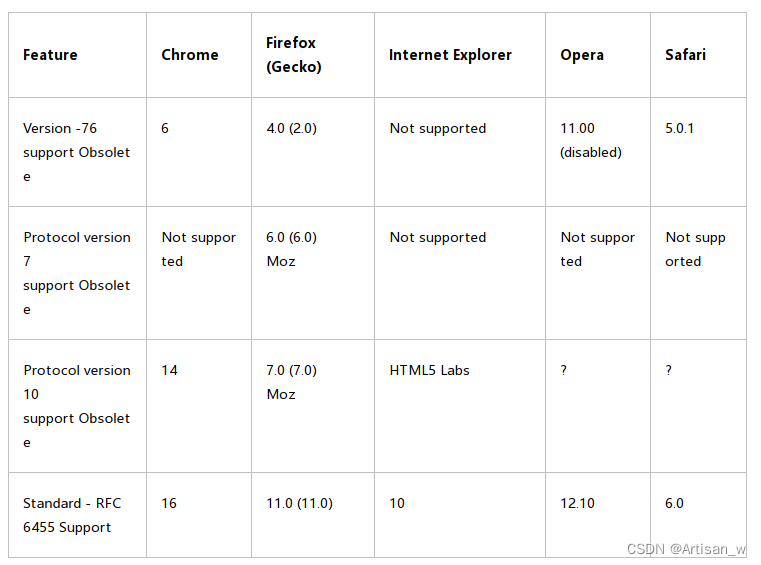
commet与websocket
commet与websocket Comet 前言 Comet是一种用于web的技术,能使服务器能实时地将更新的信息传送到客户端,而无须客户端发出请求,目前有两种实现方式,长轮询和iframe流。 实现方式 长轮询 长轮询是在打开一条连接以后保持&…...
python3 简易 http server:实现本地与远程服务器传大文件
在个人目录下创建新文件httpserver.py : vim httpserver.py文件内容为python3代码: # !/usr/bin/env python3 import datetime import email import html import http.server import io import mimetypes import os import posixpath import re import…...
Microsoft Edge 主页启动diy以及常用的扩展、收藏夹的网站
一、Microsoft Edge 主页启动diy 二、常用的扩展 1、去广告:uBlock Origin 2、翻译: 页面翻译:右键就有了,已经内置了划词翻译 3、超级复制 三、收藏夹的网站...

文末送书!谈谈原型模式在JAVA实战开发中的应用(附源码+面试题)
作者主页:Designer 小郑 作者简介:3年JAVA全栈开发经验,专注JAVA技术、系统定制、远程指导,致力于企业数字化转型,CSDN博客专家,蓝桥云课认证讲师。 本文讲解了 Java 设计模式中的原型模式,并给…...

视频汇聚/视频云存储/视频监控管理平台EasyCVR启动时打印starting server:listen tcp,该如何解决?
视频云存储/安防监控EasyCVR视频汇聚平台基于云边端智能协同,可实现视频监控直播、视频轮播、视频录像、云存储、回放与检索、智能告警、服务器集群、语音对讲、云台控制、电子地图、H.265自动转码H.264、平台级联等。为了便于用户二次开发、调用与集成,…...
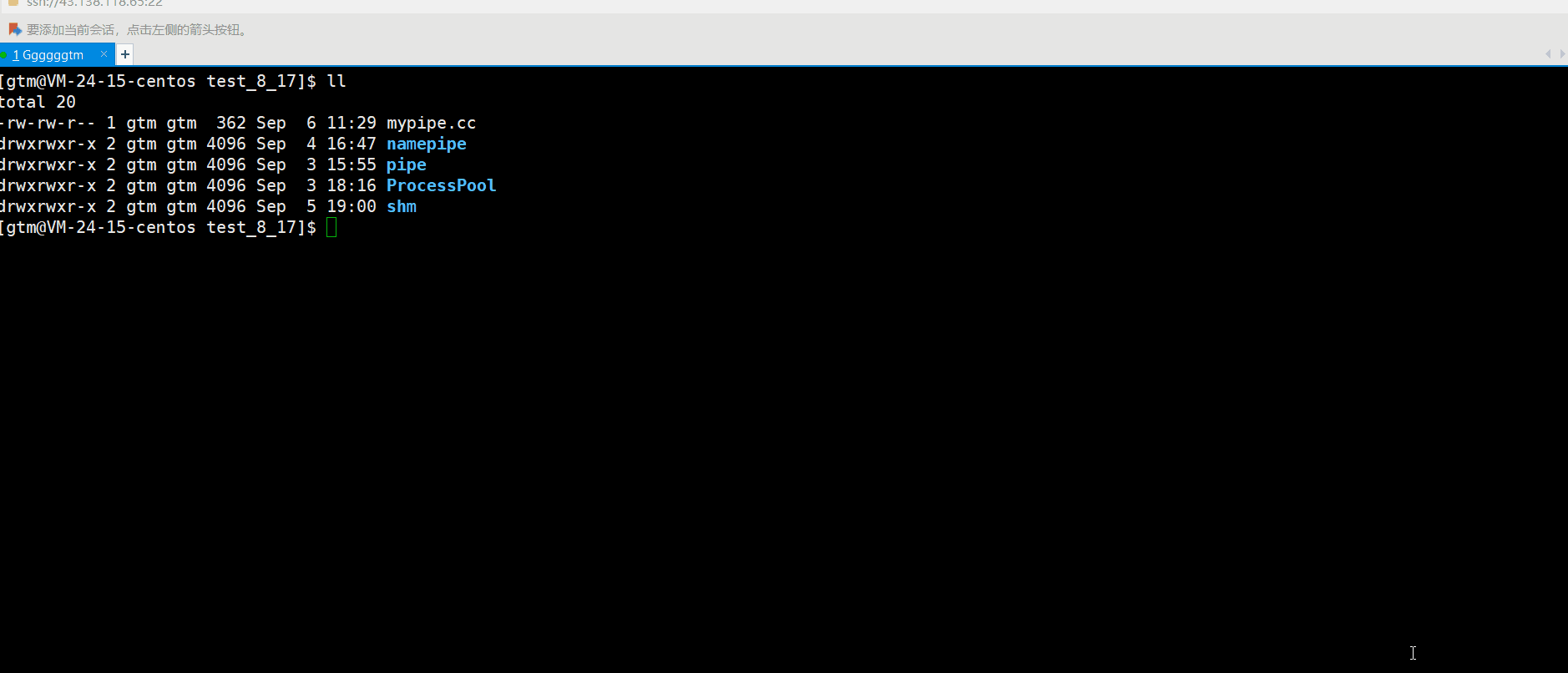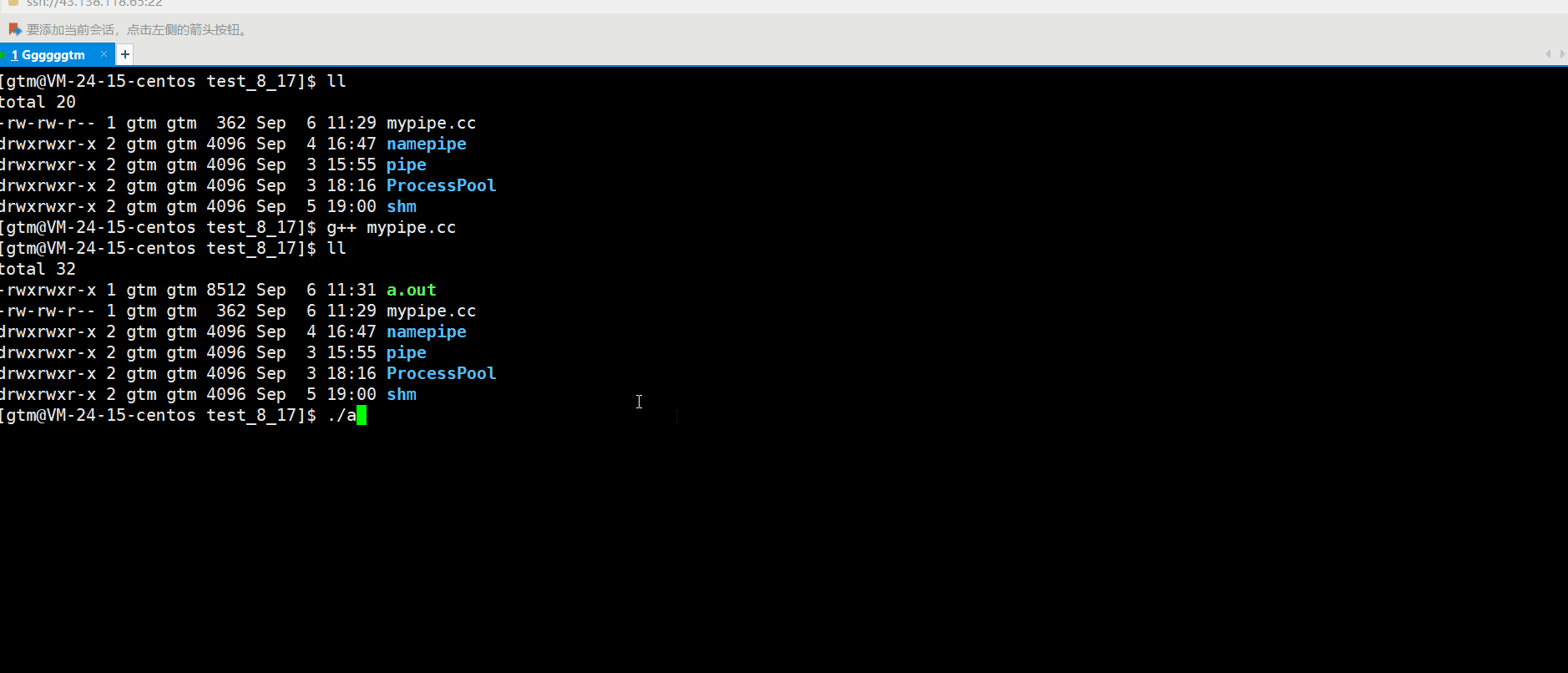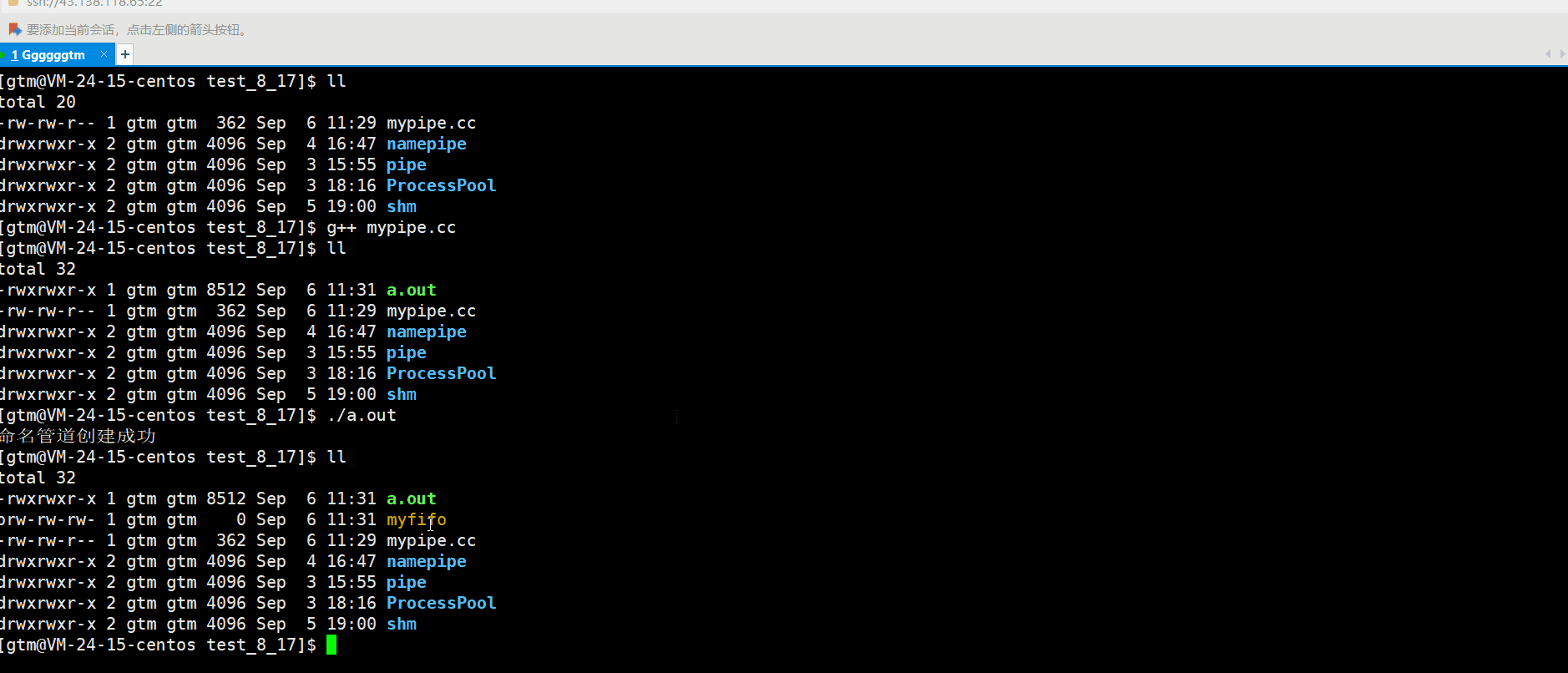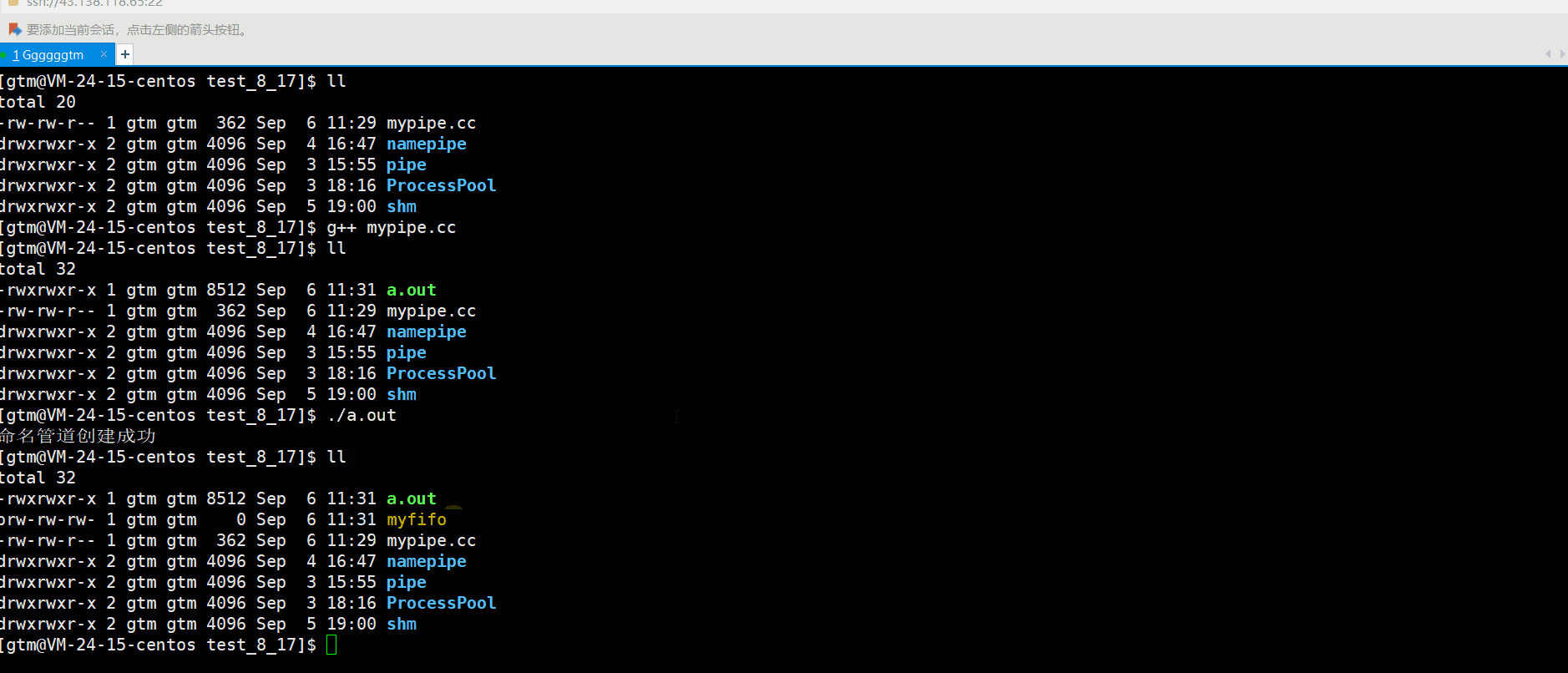
【Linux从入门到精通】通信 | 管道通信(匿名管道 命名管道)
本派你文章主要是对进程通信进行详解。主要内容是介绍 为什么通信、怎么进行通信。其中本篇文章主要讲解的是管道通信。希望本篇文章会对你有所帮助。 文章目录 一、进程通信简单介绍 1、1 什么是进程通信 1、2 为什么要进行通信 1、3 进程通信的方式 二、匿名管道 2、1 什么是…...

实践和项目:解决实际问题时,选择合适的数据结构和算法
文章目录 选择合适的数据结构数组链表栈队列树图哈希表 选择合适的算法实践和项目 🎉欢迎来到数据结构学习专栏~实践和项目:解决实际问题时,选择合适的数据结构和算法 ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:IT…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
