数据结构与算法之贪心动态规划
一:思考
1.某天早上公司领导找你解决一个问题,明天公司有N个同等级的会议需要使用同一个会议室,现在给你这个N个会议的开始和结束 时间,你怎么样安排才能使会议室最大利用?即安排最多场次的会议?电影的话 那肯定是最多加票价最高的,入场率。综合算法
2.双十一马上就要来了,小C心目中的女神在购物车加了N个东西,突然她中了一个奖可以清空购物车5000元的东西(不能找零),每个东西只能买一件,那么她应该如何选择物品使之中奖的额度能最大利用呢?如果存在多种最优组合你只需要给出一种即可,嘿嘿 现在女神来问你,你该怎么办?(动态规划)
二: 贪心算法
概念:贪心算法又叫做贪婪算法,它在求解某个问题是,总是做出眼前最大利益。 也就是说只顾眼前不顾大局,所以它是局部最优解。核心点:通过局部最优推出全局最优。
举例:
1.某天早上公司领导找你解决一个问题,明天公司有N个同等级的会议需要使用同一个会议室,现在给你这个N个会议的开始和结束时间,你怎么样安排才能使会议室最大利用?即安排最多场次的会议?
现在我们怎么去贪?也就这个我们选择的贪心策略:、
1.1 选时间最短:1-3,2~4,3~5,4~6
1.2 按结束时间从小到大排序:首先把第一个加入我们可以开会的列表。之后只要开始时间是大于我们上一个的结束时间的就可以开 (代码如下)
package tx;import java.util.ArrayList;
import java.util.List;
import java.util.Scanner;/*** 贪心算法:1.某天早上公司领导找你解决一个问题,明天公司有N个同等级的会议需要使用同一个会议室,* 现在给你这个N个会议的开始和结束时间,你怎么样安排才能使会议室最大利用?即安排最多场次的会议?** 策略:按结束时间从小到大排序:首先把第一个加入我们可以开会的列表。之后只要开始时间是大于我们上一个的结束时间的就可以开* 核心:排序*/
class Metting implements Comparable<Metting> {int meNum; // 编号int startTime; // 开始时间int endTime; // 结束时间public Metting(int meNum, int startTime, int endTime) {super();this.meNum = meNum;this.startTime = startTime;this.endTime = endTime;}public int compareTo(Metting o) {if (this.endTime > o.endTime)return 1;return -1;}@Overridepublic String toString() {return "Metting [meNum=" + meNum + ", startTime=" + startTime+ ", endTime=" + endTime + "]";}}public class MettingTest {public static void main(String[] args) {Scanner cin = new Scanner(System.in);List<Metting> mettings = new ArrayList<Metting>();int n = cin.nextInt(); //n个会议for (int i = 0 ;i < n; i++){int start = cin.nextInt();int end = cin.nextInt();Metting metting = new Metting(i+1, start, end);mettings.add(metting);}mettings.sort(null);int curTime = 0; //当前的时间,从一天的0点开始,如果领导要求从8点开始 那curTime=8for(int i = 0 ; i < n; i ++){Metting metting = mettings.get(i);if(metting.startTime >= curTime){ //会议的开始时间比我们当前的要大 表示可以开System.out.println(metting.toString());curTime = metting.endTime;}}}
}
2.1 贪心算法的核心思想
贪心算法的套路:一定会有一个排序。哈夫曼编码,贪心算法,压缩算法。最短路径
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
贪心算法其最重要的两个点就是: 贪心策略,排序
通过局部最优解能够得到全局最优解
一般通过以下问题就可以通过贪心算法解决:
1.针对某个问题有限制值,以及有一个期望的最好结果,通常是从某些数据中选出其中一些,达到最好的结果。
2.一般会有一个排序,找出贡献最大的。
3.举例看贪心是否可以解决。 一般用在任务调度,教师排课等系统。 实际上,用贪心算法解决问题的思路,并不总能给出最优解。
三:动态规划
经典问题
背包问题 小偷去某商店盗窃,背有一个背包,容量是5kg,现在有以下物品(物品不能切分,且只有一个),请问小偷应该怎么拿才能得到最大的价值?
5kg的袋子
物品:
钱:6 10 12
Kg:1 2 4
思路:我们把5kg的袋子,拆分成1kg,1kg这样子计算,里面的表格就表示当前重量下能装的最多的钱。表格的数列就表示是要装的物品
1kg
2kg
3kg
4kg
5kg
加入物品1
6
6
6
6
6
加入物品2
6
10
10+6=16
10+6=16
16
加入物品3
6
10
16
16
18
第一个物品: 袋子只能装1kg的物品,所以价钱为6
第二个物品:
袋子当前为1kg 的容量时,我们发现物品2装不进去。那我们应该取多少呢?是不是只要取物品进来时1kg最大钱?
当袋子为2kg时,我们发现物品2可以装下去,此时可以得到10块钱,之前物品1进来时2kg最大是6吧,那我们肯定要选择大的这个10,而不是6.此时袋子还剩0kg可以装。
袋子为3kg时,我们还是可以装下这个物品2,得到10块,袋子还剩下1kg。
10+1kg能装的东西。
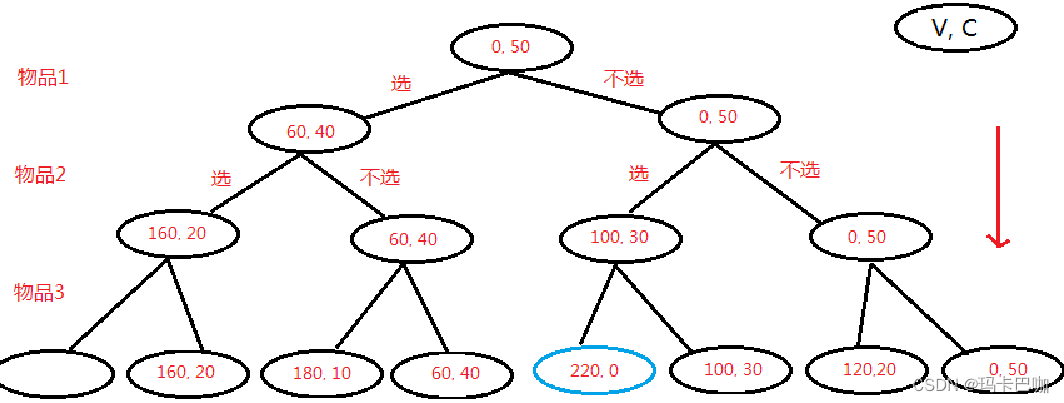
第三个物品:
袋子为4kg时,物品3可以转进来,得到12块钱,袋子还剩0kg。
我发现我不装物品3 还能得到16呢
袋子为5kg时,物品3可以转进来,得到12块钱,袋子还剩1kg。那么装了物品3就能得到12+6=18块钱
我发现我不装物品3 能得到16,比18小,所以决定装.。
(图解:将数值除以10就是上面的题)
代码实现
package tx;public class Dp {public static void main(String[] args) {int value [] ={60,100,120};int weigth[] = {10,20,40}; //购物车那个问题 只需要一个价值就行了,重量都都没有。int w = 50; //代表我可以装的数量int n = 3; //代表三个物品int dp[][] = new int[n+1][w+1]; //n表示是物品,w表示重量,初始化全是0for(int i = 1; i<= n; i++){ //每次加的物品for(int cw = 1 ; cw <= w ; cw ++){ //分割的背包if(weigth[i - 1] <= cw){ //表示这个物品可以装进去dp[i][cw] = Math.max(value[i-1] + dp[i-1][cw-weigth[i-1]],dp[i-1][cw]);}else{dp[i][cw] = dp[i-1][cw]; //不能装}}}System.out.println(dp[n][w]);}
}
四:动归和贪心的比较
贪心是只管眼前不会管后的情况,而动归不一样,它的每次递推都是基于上一次的最优解进行。所以往往动归是一定能求出最优解的,而贪心不一定,这也是贪心算法的缺点,但是大家都看到了动归的时间复杂度是O(n*m)而贪心是O(nlogn),所以贪心算法的是高效的,动归如果子问题太多的话 就容易算不出结果,而且能用动归的问题往往用贪心都能解决一部分,甚至很大一部分。因此如果在实际项目中要求不是特别严的话 我建议使用贪心算法求最优解,其实我们很多时候并不用保证100%的准确,能尽量准确就可以了,贪心恰恰是符合这个规则的。
五:购物车代码实现
package tx;public class CardDp {public static void main(String[] args) {int weigth[] = {1,2,3,4,5,9}; //购物车那个问题 只需要一个价值就行了,重量都都没有。int w = 8;int n = 6;int dp[][] = new int[n+1][w+1]; //n表示是物品,w表示重量,初始化全是0for(int i = 1; i<= n; i++){ //每次加的物品for(int cw = 1 ; cw <= w ; cw ++){ //分割的背包if(weigth[i - 1] <= cw){ //表示这个物品可以装进去dp[i][cw] = Math.max(weigth[i-1] + dp[i-1][cw-weigth[i-1]],dp[i-1][cw]);}else{dp[i][cw] = dp[i-1][cw]; //不能装}}}System.out.println(dp[n][w]);}
}
相关文章:
数据结构与算法之贪心动态规划
一:思考 1.某天早上公司领导找你解决一个问题,明天公司有N个同等级的会议需要使用同一个会议室,现在给你这个N个会议的开始和结束 时间,你怎么样安排才能使会议室最大利用?即安排最多场次的会议?电影的话 那…...

【网络编程】网络基础概念
(꒪ꇴ꒪ ),Hello我是祐言QAQ我的博客主页:C/C语言,数据结构,Linux基础,ARM开发板,网络编程等领域UP🌍快上🚘,一起学习,让我们成为一个强大的攻城狮࿰…...
连接虚拟机报错 Could not connect to ‘192.168.xxx.xxx‘ (port 22): Connection failed.
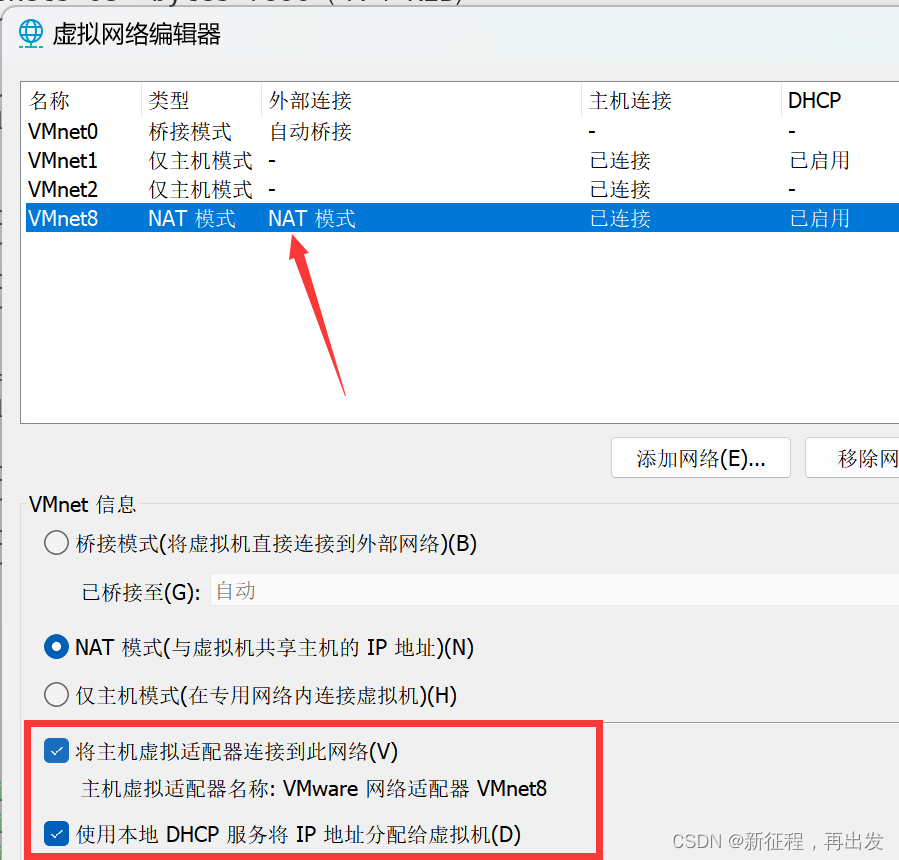
使用xshell连接虚拟机报错 Connecting to 192.168.204.129:22… Could not connect to ‘192.168.204.129’ (port 22): Connection failed. Type help’ to learn how to use Xshell prompt. 按网上的方法 是否能ping通内外网 ping www.baidu.com防火墙是否关闭 firewal…...
数学建模--Topsis评价方法的Python实现
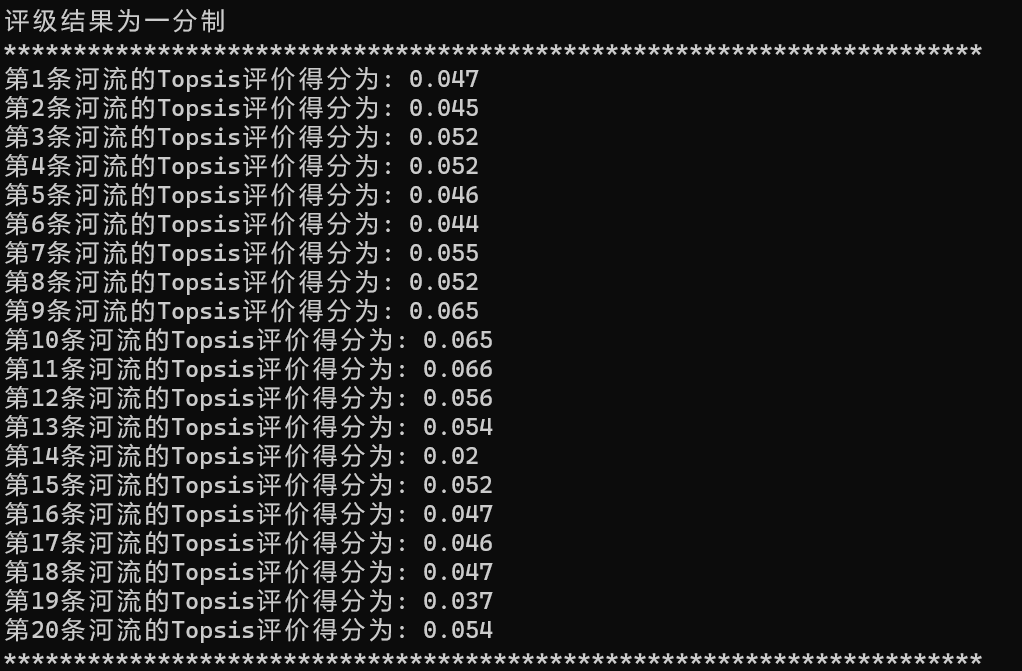
目录 1.算法流程简介 2.算法核心代码 3.算法效果展示 1.算法流程简介 """ TOPSIS(综合评价方法):主要是根据根据各测评对象与理想目标的接近程度进行排序. 然后在现有研究对象中进行相对优劣评价。 其基本原理就是求解计算各评价对象与最优解和最劣解的距离…...

超越时间与人力的软件开发智慧:《人月神话》
目录 1、写在前面2、沟通!沟通!沟通!3、“银弹论”4、“人月神话”不能成立的原因5、影响力6、图书推荐 1、写在前面 《人月神话》是由计算机科学家弗雷德里克布鲁克斯所著的一本经典著作,首次出版于1975年。这本书以一个个小故事…...

Java Stream 流对象(实用技巧)
目录 一、InputStream & OutputStream 1.1、InputStream 和 OutputStream 一般使用 1.2、特殊使用 1.2.1、如何表示文件读取完毕?(DataInputStream) 1.2.2、字符读取/文本数据读取(Scanner) 1.2.3、文件的随机…...

【用unity实现100个游戏之8】用Unity制作一个炸弹人游戏
文章目录 前言素材开始一、绘制地图二、玩家设置三、玩家移动四、玩家四方向动画运动切换 五、放置炸弹六、生成爆炸效果七、墙壁和可破坏障碍物的判断八、道具生成和效果九、玩家死亡十、简单的敌人AI十一、简单敌人AI十二、随机绘制地图十三、虚拟摇杆 最终效果待续源码完结 …...

简易版人脸识别qt opencv
1、配置文件.pro #------------------------------------------------- # # Project created by QtCreator 2023-09-05T19:00:36 # #-------------------------------------------------QT core guigreaterThan(QT_MAJOR_VERSION, 4): QT widgetsTARGET 01_face TEMP…...

如何系统地学习 JavaScript?
前言 在学习JavaScript前需要先将Html和Css的相关知识点弄清楚,Js的很多操作是要结合Html和Css,下面我总结了Html、Css和Js的相关学习知识点供参考,希望对你有所帮助喔~ Html 文档学习 【HTML 】w3school教程 :https://www.w3school.com.…...
)
对称二叉树(Leetcode 101)
题目 101. 对称二叉树 思路 使用层序遍历,遍历当前层的节点时,如该节点的左(右)孩子为空,在list中添加null,否则加入左(右)孩子的值。每遍历完一层则对当前list进行判断,…...
-3.5 图像分类数据集)
动手学深度学习(2)-3.5 图像分类数据集
文章目录 引言正文图像分类数据集主要包介绍主要流程具体代码练习 总结 引言 这里主要是看一下如何加载数据集,并且生成批次训练的数据。最大的收获是,知道了如何在训练阶段提高模型训练的性能 增加batch_size增加num_worker数据预加载 正文 图像分类…...

C标准输入与标准输出——stdin,stdout
🔗 《C语言趣味教程》👈 猛戳订阅!!! —— 热门专栏《维生素C语言》的重制版 —— 💭 写在前面:这是一套 C 语言趣味教学专栏,目前正在火热连载中,欢迎猛戳订阅&#…...
如何将home目录空间扩充到根目录下
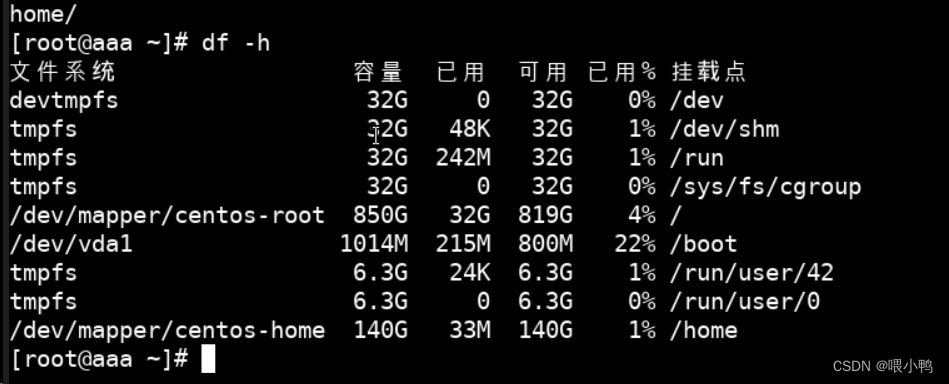
目录 1、查看查看磁盘使用情况2、扩容思路3、卸载并删除/home4、扩大/root逻辑卷5、扩大/文件系统6、重建/home逻辑卷7、创建/home文件系统8、将新建的文件系统挂载到/home目录下9、恢复/home并删除备份10、再次查看看磁盘存储 系统:centos7.9 1、查看查看磁盘使用…...

Ceph PG Peering数据修复
ceph数据修复 当PG完成了Peering过程后,处于Active状态的PG就可以对外提供服务了。如果该PG的各个副本上有不一致的对象,就需要进行修复。 Ceph的修复过程有两种:Recovery和Backfill。 Recovery是仅依据PG日志中的缺失记录来修复不一致的对…...

服务器上使用screen和linux的基本操作
临时换源 pip install torch1.7.1 -i https://pypi.tuna.tsinghua.edu.cn/simple some-package pip install torch1.7.1 -i http://pypi.douban.com/simple some-package临时清华源和豆瓣源 配环境的一点小问题 我们尽量是去配置能满足代码的环境,而不要想着修改…...

Kafka3.0.0版本——文件存储机制
这里写木目录标题 一、Topic 数据的存储机制1.1、Topic 数据的存储机制的概述1.2、Topic 数据的存储机制的图解1.3、Topic 数据的存储机制的文件解释 二、Topic数据的存储位置示例 一、Topic 数据的存储机制 1.1、Topic 数据的存储机制的概述 Topic是逻辑上的概念,…...

Linux如何安装MySQL
Linux安装MySQL5.7 1、下载 官网下载地址:http://dev.mysql.com/downloads/mysql/ 2、复制下面几个文件 3、检查当前系统是否安装过mysql、检查当前mysql依赖环境、检查/tmp文件夹权限 1)检查当前系统是否安装过mysql,执行安装命令前&am…...

确保网络的安全技术介绍
防火墙技术 防火墙是隔离本地网络与外界网络的一道防御系统。通常用于内部局域网 与外部广域网之间,通过限制外部网络用户以非法手段来访问内部资源,来达到保 护内部网络的安全。根据安全规则,防火墙对任何外部网络访问内部网络的行为进 …...

机器学习练习
原文章添加链接描述...

算法通关村第十九关——最小路径和
LeetCode64. 给定一个包含非负整数的 m n 网格 grid,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。 输入:grid[[1,3,1],[1,5,1],[4,2,1]] 输出:7 解释:因为路径1→3→1→1→1的总和最小。 public int minPath…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...
