JS中数组如何去重(ES6新增的Set集合类型)+经典two sum面试题
现在有这么一个重复数组:
const arr = ['a','a','b','a','b','c']只推荐简单高效的方法,复杂繁琐的方法不做推荐
方法一:
const res = [...new Set(arr)]Set类型是什么呢?
Set 是ES6新增的一种新集合类型。具体知识点可以看下面附录:
根据上面的知识点,我们可以得到:
console.log(...new Set(arr)) // a b c所以去重也可以这么实现:
const res = Array.from(new Set(arr)) // Array.from将类数组转换成数组
// or
const res = Array.of(...new Set(arr)) // Array.of根据传入的参数生成数组方法二:
var arr = ['apple','apps','pear','apple','orange','apps'];
var newArr = arr.filter(function(item,index){return arr.indexOf(item) === index; // 因为indexOf 只能查找到第一个
});方法三:
some + 循环去重
function distinct(list) {let result = [list[0]];// 用于承接没有重复的数据,初始时将原始数组的第一个值赋给它。for (let i = 1; i < list.length; i++) {// 判断结果数组中是否存在一样的值,若果没有的话则将数据存入结果数组中。if (!(result.some(val => list[i] === val))) {result.push(list[i]);}}return result;}方法四:
如果不能用ES6、5的语法。需要原生方法双重for循环去重:
function noRepeat(arr) {for(var i = 0; i < arr.length-1; i++){for(var j = i+1; j < arr.length; j++){if(arr[i]===arr[j]){arr.splice(j,1);j--;}}}return arr;}方法五:
简单数组用includes去重
function noRepeat(arr) {let newArr = [];for(i=0; i<arr.length; i++){if(!newArr.includes(arr[i])){newArr.push(arr[i])}}return newArr
}附录 -Set
使用 new 关键字和 Set 构造函数可以创建一个空集合:
const s = new Set();如果想在创建的同时初始化实例,则可以给 Set 构造函数传入一个可迭代对象(Array Map Set WeakMap WeakSet)。可迭代对象需要包含插入到新集合实例中的元素(Set 可以包含任何 JavaScript 数据类型作为值)。Set构造函数会迭代传入参数,去重后保存到集合实例中。
特点
Set 是唯一值的集合。
每个值在 Set 中只能出现一次。
一个 Set 可以容纳任何数据类型的任何值。
你可以把Set想像成跟数组一样,我们用size来输出Set集合的长度。
const s = new Set(['a','b','c','c']);
s.size; // 3 去重了一个c
const s2 = new Set();
s2.add('a')
s2.add('b')
s2.add('c')
s2.size // 3与Array的区别
最根本的区别是数组是一个索引集合,这说明数组中的数据值按索引排序。
相比之下,set是一个键的集合。set不使用索引,而是使用键对数据排序(看下面forEach)。set 中的元素按插入顺序是可迭代的,它不能包含任何重复的数据。
对比Array的优势
在运行时间方面上Set占了很大的优势
查看元素:使用indexOf()或includes()检查数组中的项是否存在是比较慢的。
删除元素:在Set中,可以根据每项的的 value 来删除该项。在数组中,等价的方法是使用基于元素的索引的splice()。与前一点一样,依赖于索引的速度很慢。
保存 NaN:不能使用indexOf()或 includes() 来查找值 NaN,而 Set 可以保存此值。
删除重复项:Set对象只存储惟一的值,如果不想有重复项存在,相对于数组的一个显著优势,因为数组需要额外的代码来处理重复。
时间复杂度:
数组用来搜索元素的方法时间复杂度为0(N)。换句话说,运行时间的增长速度与数据大小的增长速度相同。
相比之下,Set用于搜索、删除和插入元素的方法的时间复杂度都只有O(1),这意味着数据的大小实际上与这些方法的运行时间无关。
具体解释与面试题强烈推荐阅读如何使用 Set 来提高JS代码的性能 - 知乎 (zhihu.com)
其他API
has()
查询Set实例是否存在某元素(返回布尔值):
const s = new Set();
s.add(1).add(2).add(3);
s.has(1); // truedelete()
删除某个元素
s.delete(1);clear()
清空Set实例
s.clear();
Array.from(s); // []迭代:
for of
for in不输出,因为它不是以下标为索引的集合
const s = new Set(['a','b','c','c']);
for (var n of s) {console.log(n)}
// a
// b
// cforEach
s.forEach((t,i)=>console.log(t,i))
// a a
// b b
// c c
// 输出了键值对的结构原生属性

可以看见Set实例的三个属性返回了枚举的类数组。
直接用Array.form转换
Array.from(s.keys())
// ['a', 'b', 'c']
Array.from(s.entries())
// [['a', 'a'],['b', 'b'],['c', 'c']]
Array.from(s.values())
// ['a', 'b', 'c']附录-面试题
题目:
给定一个整数无序数组和变量 sum,如果存在数组中任意两项和使等于 sum 的值,则返回true。否则,返回false。例如,数组[3,5,1,4]和 sum = 9,函数应该返回true,因为4 + 5 = 9。
解题思路:
本题其实是为了找数组元素与sum的差值是否在数组里重复出现。

const s = new Set()
arr.some(t=> {if (s.has(t)) {return true}s.add(sum-t);return fasle
})简洁点写:
const findSum = (arr, sum) =>arr.some((set => n => set.has(n) || !set.add(sum - n))(new Set));相关文章:

JS中数组如何去重(ES6新增的Set集合类型)+经典two sum面试题
现在有这么一个重复数组:const arr [a,a,b,a,b,c]只推荐简单高效的方法,复杂繁琐的方法不做推荐方法一:const res [...new Set(arr)]Set类型是什么呢?Set 是ES6新增的一种新集合类型。具体知识点可以看下面附录:根据…...
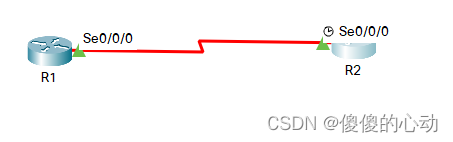
HDLC简介及相应hdlc实训
HDLC简介 HDLC 协议 高级数据链路控制(HDLC,High-level Data Link Control)是一种面向比特的链路层协议, 其最大特点是对任何一种比特流,均可以实现透明的传输。HDLC协议具有以下优点。 透明传输:HDLC不…...
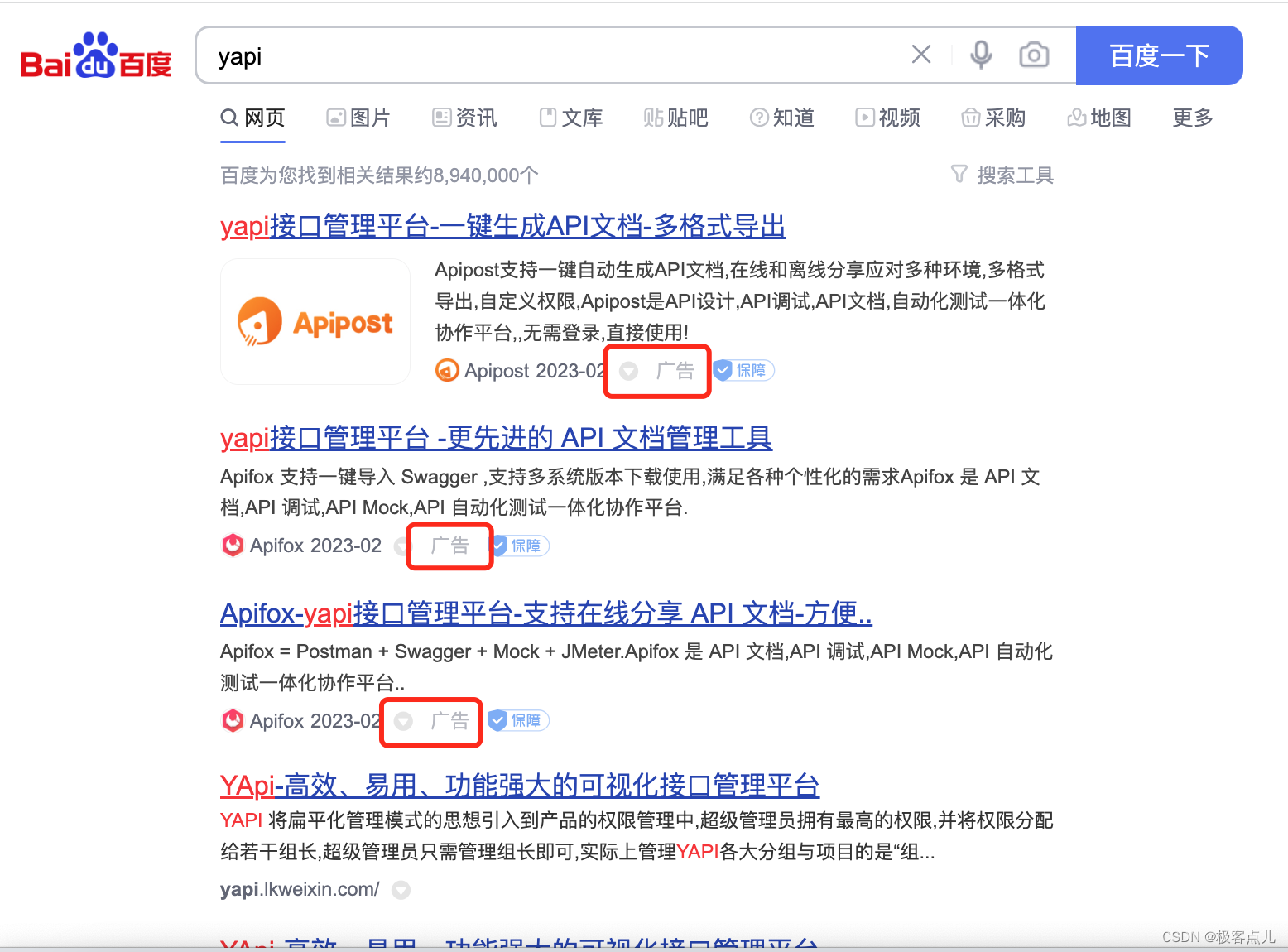
公司技术团队为什么选择使用 YApi 作为 Api 管理平台?
在 2021 年 12 月份的时候我就推荐过一款软件程序员软件推荐:Apifox,当时体验了一下里面的功能确实很实用,但是当时公司有一套自己的 API 管理方案,所有 Apifox 暂时就没在内部使用。 直到最近要使用其他的 API 管理方案的时候才…...

ts知识点整理
1、ts 中的 any 和 unknown 有什么区别? any 和 unknown 都是顶级类型,但是 unknown 更加严格,不像 any 那样不做类型检查,反而 unknown 因为未知性质,不允许访问属性,不允许赋值给其他有明确类型的变量。…...

技术分享 | OceanBase 数据处理之控制文件
作者:杨文 DBA,负责客户项目的需求与维护,会点数据库,不限于MySQL、Redis、Cassandra、GreenPlum、ClickHouse、Elastic、TDSQL等等。 本文来源:原创投稿 *爱可生开源社区出品,原创内容未经授权不得随意使用…...
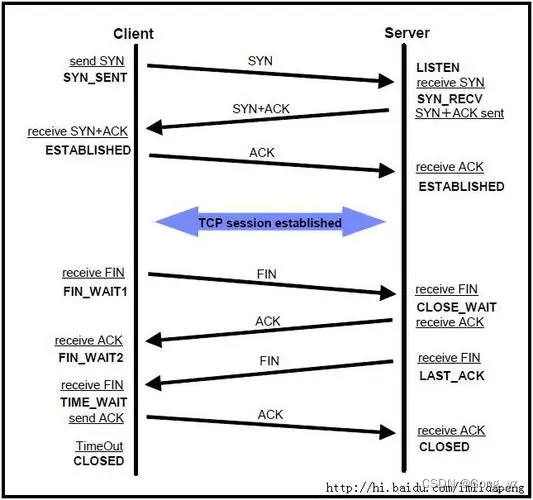
TCP的三次握手、四次挥手
文章目录前言一、一些重要字段的含义二、TCP总括图三、三次握手详细过程1.第一次握手2.第二次握手3.第三次握手三次握手小结4.为什么必须要进行三次握手,两次或四次就不行四、四次挥手1.第一次挥手2.第二次挥手3.第三次挥手4.第四次挥手四次挥手简述前言 一个TCP的…...

C++---特殊类的设计
文章目录前言一、请设计一个类,不能被拷贝二、请设计一个类,只能在堆上创建对象三、请设计一个类,只能在栈上创建对象四、请设计一个类,不能被继承五、请设计一个类,只能创建一个对象(单例模式)总结前言 正文开始! 一、请设计一个类,不能被拷贝 拷贝只会发生在两个…...

buu [WUSTCTF2020]dp_leaking_1s_very_d@angerous 1
题目描述: e 65537 n 1568083435985787749573756968151889806821667406093028310996964920682463371987925108988184962391663390152073051021014316342831685444929845865667999964711502523821441482572367072472675061656708775063702531276953141639870840764…...

基于SVPWM改进的永磁同步电机直接转矩控制二更
导读:本期对基于SVPWM的永磁同步电机直接转矩控制进行全面的分析和仿真搭建。之后与传统的DTC进行比较,凸显基于SVPWM改进的DTC方法的有效性。如果需要文中的仿真模型,关注微信公众号:浅谈电机控制,留言获取。一、 传统…...

ubuntu下磁盘管理
一. ubuntu 磁盘文件 在做 Linux 嵌入式开发中,一般选择 U 盘的要求是:确保 U 盘是 FAT格式,即选用 FAT32 格式的U盘或 SD 卡。不要用 NTFS 格式的 U 盘或 SD卡,因为Linux 大多数系统都不支持 NTFS格式的,NTFS 格式的…...

Python学习-----排序问题1.0(冒泡排序、选择排序、插入排序)
目录 前言: 1.冒泡排序 2.选择排序 3.插入排序 前言: 学过C语言肯定接触过排序问题,我们最常用的也就是冒泡排序、选择排序、插入排序……等等,同样在Python中也有排序问题,这里我也会讲解Python中冒泡排序、选择排…...
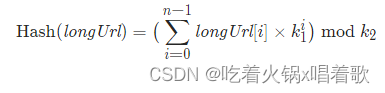
LeetCode 535. TinyURL 的加密与解密
TinyURL 是一种 URL 简化服务, 比如:当你输入一个 URL https://leetcode.com/problems/design-tinyurl 时,它将返回一个简化的URL http://tinyurl.com/4e9iAk 。请你设计一个类来加密与解密 TinyURL 。 加密和解密算法如何设计和运作是没有限…...

【c++】类和对象2—构造函数、析构函数、拷贝构造函数
文章目录构造函数和析构函数构造函数的分类及调用拷贝构造函数调用时机构造函数调用规则深拷贝与浅拷贝构造函数和析构函数 c利用了构造函数和析构函数解决上述问题,这两个函数将会被编译器自动调用,完成对象初始化和清理工作。对象的初始化和清理工作是…...

[C++关键字] const/constexpr
文章目录const/constexpr[^1]const 与 宏const 与 类const 与 指针const 其他constexpr (C11之后)referenceconst/constexpr1 尽可能的使用constexpr对于不变的变量,尽量用const修饰 const 与 宏 const vs define的比较:define只是字符的替换…...
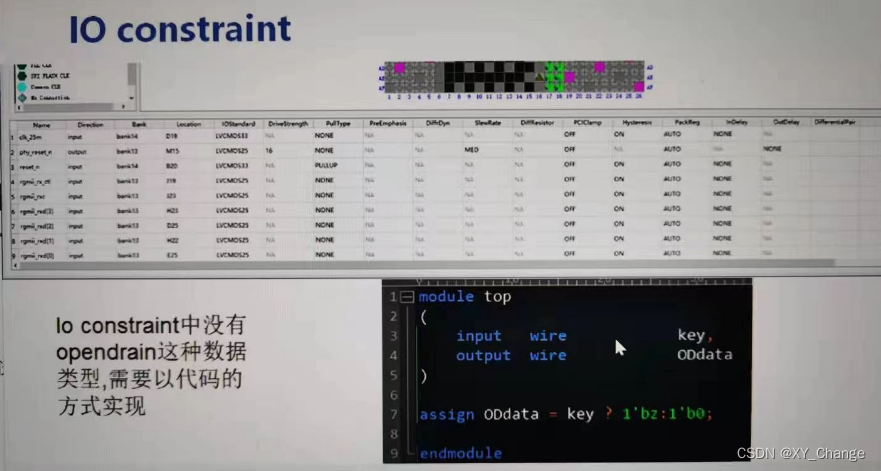
FPGA电源电流参数
一、FPGA里各个电源释义 VCCINT VCCINT是FPGA芯片的内核电压,是用来给FPGA内部的逻辑门和触发器上的电压。即芯片的晶体管开关是有核心电压提供。当内部逻辑工作时钟速率越高,使用逻辑资源越多,则核心电压供电电流会更大,可高达几…...

【Git】Git下载安装与使用(一)
目录 1. 前言 1.1 什么是Git 1.2 使用Git能做什么 2. Git概述 2.1 Git简介 2.2 Git下载与安装 3. Git代码托管服务 3.1 常用的Git代码托管服务 3.2 码云代码托管服务 1. 前言 1.1 什么是Git Git是一个分布式版本控制工具,主要用于管理开发过程中的源代码…...

刷题记录:牛客NC20545[HEOI2012]采花
传送门:牛客 题目描述: 题目较长,此处暂略 输入: 5 3 5 1 2 2 3 1 1 5 1 2 2 2 2 3 3 5 输出: 2 0 0 1 0总结一下题意,就是求区间[l,r][l,r][l,r]出现次数大于1的花的种类数. 考虑使用主席树或者离线树状数组的方法来解决.由于数据加强的原因,导致主席树在本题中是不能完美通…...

每日学术速递2.21
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.T2I-Adapter: Learning Adapters to Dig out More Controllable Ability for Text-to-Image Diffusion Models 标题:T2I-Adapter:学习Adapter,为…...
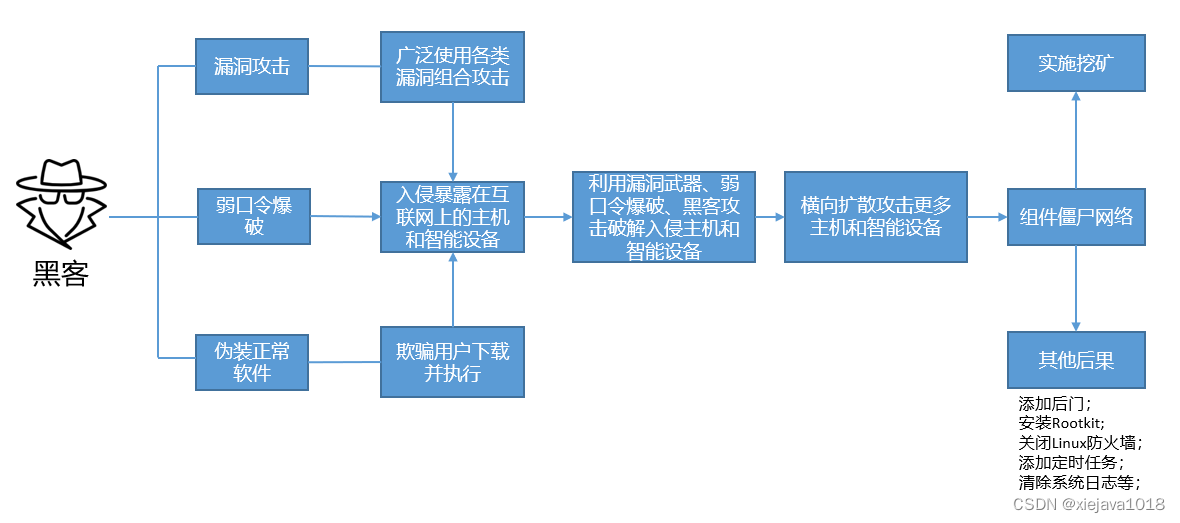
网络安全之认识挖矿木马
一、什么是挖矿木马? 比特币是以区块链技术为基础的虚拟加密货币,比特币具有匿名性和难以追踪的特点,经过十余年的发展,已成为网络黑产最爱使用的交易媒介。大多数勒索病毒在加密受害者数据后,会勒索代价高昂的比特币…...
OpenCV实战——基于分水岭算法的图像分割
OpenCV实战——基于分水岭算法的图像分割0. 前言1. 分水岭算法2. 分水岭算法直观理解3. 完整代码相关链接0. 前言 分水岭变换是一种流行的图像处理算法,用于快速将图像分割成同质区域。分水岭变换主要基于以下思想:当图像被视为拓扑浮雕时,均…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
