buu [WUSTCTF2020]dp_leaking_1s_very_d@angerous 1
题目描述:
e = 65537
n = 156808343598578774957375696815188980682166740609302831099696492068246337198792510898818496239166339015207305102101431634283168544492984586566799996471150252382144148257236707247267506165670877506370253127695314163987084076462560095456635833650720606337852199362362120808707925913897956527780930423574343287847
c = 108542078809057774666748066235473292495343753790443966020636060807418393737258696352569345621488958094856305865603100885838672591764072157183336139243588435583104423268921439473113244493821692560960443688048994557463526099985303667243623711454841573922233051289561865599722004107134302070301237345400354257869
dp = 734763139918837027274765680404546851353356952885439663987181004382601658386317353877499122276686150509151221546249750373865024485652349719427182780275825
题目分析:
- 首先我们先看下解题脚本,再进行分析:
e = 65537
n = 156808343598578774957375696815188980682166740609302831099696492068246337198792510898818496239166339015207305102101431634283168544492984586566799996471150252382144148257236707247267506165670877506370253127695314163987084076462560095456635833650720606337852199362362120808707925913897956527780930423574343287847
c = 108542078809057774666748066235473292495343753790443966020636060807418393737258696352569345621488958094856305865603100885838672591764072157183336139243588435583104423268921439473113244493821692560960443688048994557463526099985303667243623711454841573922233051289561865599722004107134302070301237345400354257869
dp = 734763139918837027274765680404546851353356952885439663987181004382601658386317353877499122276686150509151221546249750373865024485652349719427182780275825
for i in range(1,65535):p = (dp*e-1)//i+1if n%p == 0:q = n//pbreak
# print(p)
# print(q)
phi = (p-1)*(q-1)
d = gmpy2.invert(e,phi)
m = pow(c,d,n)
flag = libnum.n2s(int(m)).decode()
print(flag)
- 主要还是这串代码—>
 有点不太理解,那下面具体来分析这串代码的由来
有点不太理解,那下面具体来分析这串代码的由来

已知:
c = m^e mod n
m = c^d mod n
ϕ(n)=(p−1)*(q−1)
d∗e ≡ 1 mod ϕ(n)
dp = d mod (p−1)
由上式可以得到
dpe≡de mod (p−1)
因此可以得到
式1:d∗e=k∗(p−1)+dp∗e
式2:d∗e≡1 mod ϕ(n)
式1带入式2
=> k∗(p−1)+dp∗e ≡1 mod ϕ(n)
=> k∗(p−1)+dp∗e ≡1 mod (p−1)∗(q−1)
=> k1∗(p−1)+dp∗e = k2*(p−1)∗(q−1)+1
=> dp * e = k2*(p−1)∗(q−1)+1-k1∗(p−1)+dp∗e
=> dp * e = (p-1)[k2(p-1)-k1]+1
因dp<p−1(dp是d//(p-1)的取整,dp<p−1)
所以e > k2∗(q−1)−k1
再次回到
dp * e = (p-1) * [k2*(p-1)-k1]+1
假设 x=k2∗(q−1)−k1
那么x的范围为 (0,e)
x∗(p−1)+1=dp∗e
枚举 x 求出p-1,即遍历(0,e)的范围,其中肯定有一个p可以被n整除,那么求出p和q
- 最终运行代码得到 flag{dp_leaking_1s_very_d@angerous} (嚯!原来题目就是答案啊!)
收获与体会:
- 知道了求dp泄露的题
- 理解了原理
相关文章:

buu [WUSTCTF2020]dp_leaking_1s_very_d@angerous 1
题目描述: e 65537 n 1568083435985787749573756968151889806821667406093028310996964920682463371987925108988184962391663390152073051021014316342831685444929845865667999964711502523821441482572367072472675061656708775063702531276953141639870840764…...

基于SVPWM改进的永磁同步电机直接转矩控制二更
导读:本期对基于SVPWM的永磁同步电机直接转矩控制进行全面的分析和仿真搭建。之后与传统的DTC进行比较,凸显基于SVPWM改进的DTC方法的有效性。如果需要文中的仿真模型,关注微信公众号:浅谈电机控制,留言获取。一、 传统…...

ubuntu下磁盘管理
一. ubuntu 磁盘文件 在做 Linux 嵌入式开发中,一般选择 U 盘的要求是:确保 U 盘是 FAT格式,即选用 FAT32 格式的U盘或 SD 卡。不要用 NTFS 格式的 U 盘或 SD卡,因为Linux 大多数系统都不支持 NTFS格式的,NTFS 格式的…...

Python学习-----排序问题1.0(冒泡排序、选择排序、插入排序)
目录 前言: 1.冒泡排序 2.选择排序 3.插入排序 前言: 学过C语言肯定接触过排序问题,我们最常用的也就是冒泡排序、选择排序、插入排序……等等,同样在Python中也有排序问题,这里我也会讲解Python中冒泡排序、选择排…...
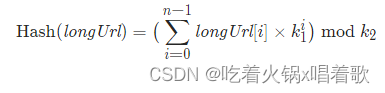
LeetCode 535. TinyURL 的加密与解密
TinyURL 是一种 URL 简化服务, 比如:当你输入一个 URL https://leetcode.com/problems/design-tinyurl 时,它将返回一个简化的URL http://tinyurl.com/4e9iAk 。请你设计一个类来加密与解密 TinyURL 。 加密和解密算法如何设计和运作是没有限…...

【c++】类和对象2—构造函数、析构函数、拷贝构造函数
文章目录构造函数和析构函数构造函数的分类及调用拷贝构造函数调用时机构造函数调用规则深拷贝与浅拷贝构造函数和析构函数 c利用了构造函数和析构函数解决上述问题,这两个函数将会被编译器自动调用,完成对象初始化和清理工作。对象的初始化和清理工作是…...

[C++关键字] const/constexpr
文章目录const/constexpr[^1]const 与 宏const 与 类const 与 指针const 其他constexpr (C11之后)referenceconst/constexpr1 尽可能的使用constexpr对于不变的变量,尽量用const修饰 const 与 宏 const vs define的比较:define只是字符的替换…...
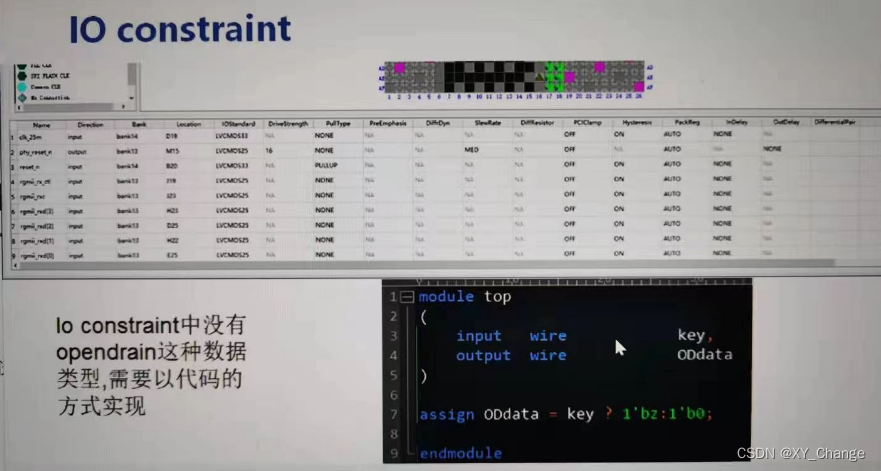
FPGA电源电流参数
一、FPGA里各个电源释义 VCCINT VCCINT是FPGA芯片的内核电压,是用来给FPGA内部的逻辑门和触发器上的电压。即芯片的晶体管开关是有核心电压提供。当内部逻辑工作时钟速率越高,使用逻辑资源越多,则核心电压供电电流会更大,可高达几…...

【Git】Git下载安装与使用(一)
目录 1. 前言 1.1 什么是Git 1.2 使用Git能做什么 2. Git概述 2.1 Git简介 2.2 Git下载与安装 3. Git代码托管服务 3.1 常用的Git代码托管服务 3.2 码云代码托管服务 1. 前言 1.1 什么是Git Git是一个分布式版本控制工具,主要用于管理开发过程中的源代码…...

刷题记录:牛客NC20545[HEOI2012]采花
传送门:牛客 题目描述: 题目较长,此处暂略 输入: 5 3 5 1 2 2 3 1 1 5 1 2 2 2 2 3 3 5 输出: 2 0 0 1 0总结一下题意,就是求区间[l,r][l,r][l,r]出现次数大于1的花的种类数. 考虑使用主席树或者离线树状数组的方法来解决.由于数据加强的原因,导致主席树在本题中是不能完美通…...

每日学术速递2.21
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.T2I-Adapter: Learning Adapters to Dig out More Controllable Ability for Text-to-Image Diffusion Models 标题:T2I-Adapter:学习Adapter,为…...
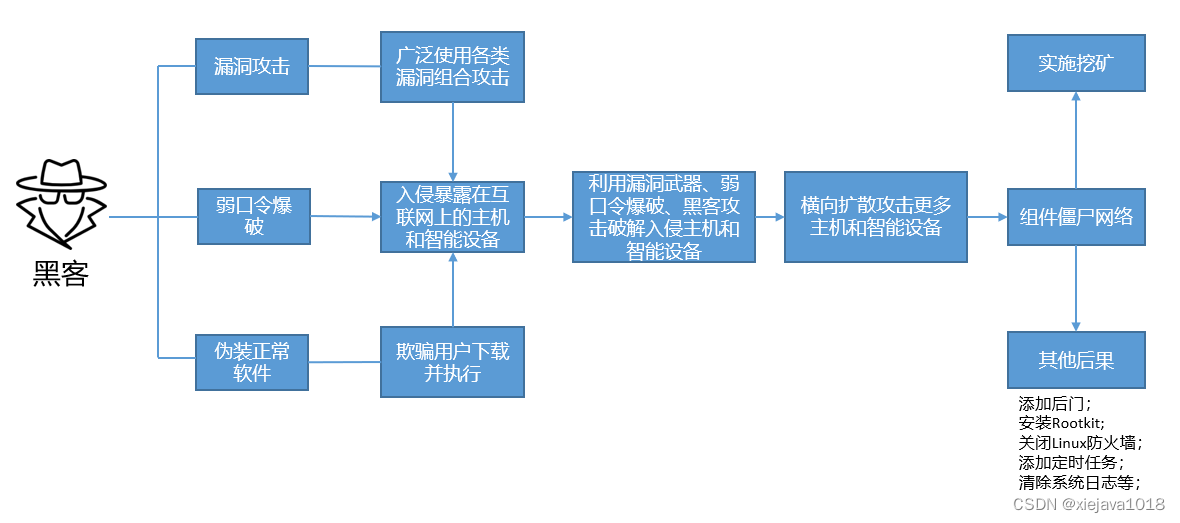
网络安全之认识挖矿木马
一、什么是挖矿木马? 比特币是以区块链技术为基础的虚拟加密货币,比特币具有匿名性和难以追踪的特点,经过十余年的发展,已成为网络黑产最爱使用的交易媒介。大多数勒索病毒在加密受害者数据后,会勒索代价高昂的比特币…...
OpenCV实战——基于分水岭算法的图像分割
OpenCV实战——基于分水岭算法的图像分割0. 前言1. 分水岭算法2. 分水岭算法直观理解3. 完整代码相关链接0. 前言 分水岭变换是一种流行的图像处理算法,用于快速将图像分割成同质区域。分水岭变换主要基于以下思想:当图像被视为拓扑浮雕时,均…...

YOLOv8模型调试记录
前言 新年伊始,ultralytics 公司在 2023 年 1月 10 号开源的 YOLOv5 的下一个重大更新版本,目前支持图像分类、物体检测和实例分割任务,在还没有开源时就收到了用户的广泛关注。 值得一提的是,在博主的印象中,YOLO系…...

算法刷题打卡第97天:删除字符串两端相同字符后的最短长度
删除字符串两端相同字符后的最短长度 难度:中等 给你一个只包含字符 a,b 和 c 的字符串 s ,你可以执行下面这个操作(5 个步骤)任意次: 选择字符串 s 一个 非空 的前缀,这个前缀的所有字符都相…...
---使用IndexBuffer(索引缓冲区))
WebGPU学习(3)---使用IndexBuffer(索引缓冲区)
现在让我们将 IndexBuffer 与 VertexBuffer 一起使用。演示示例 1.准备索引数据 我们用 Uint16Array 类型来准备索引数据。我们将矩形的4个点放到 VertexBuffer 中,然后根据三角形绘制顺序,组织成 0–1–2 和 0–2–3 的结构。 const quadIndexArray …...

Java代码加密混淆工具有哪些?
在Java中,代码加密混淆工具可以帮助开发者将源代码进行加密和混淆处理,以增加代码的安全性和保护知识产权。以下是一些流行的Java代码加密混淆工具: 第一款:ProGuard:ProGuard ProGuard:ProGuard…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 高效的任务规划(Python) | 机试题+算法思路+考点+代码解析 【2023】
高效的任务规划 题目 你有 n 台机器编号为1-n,每台都需要完成一项工作, 机器经过配置后都能独立完成一项工作。 假设第i台机器你需要花 Bi 分钟进行设置, 然后开始运行,Ji分钟后完成任务。 现在,你需要选择布置工作的顺序,使得用最短的时间完成所有工作。 注意,不能同…...

ChatGPT写程序如何?
前言ChatGPT最近挺火的,据说还能写程序,感到有些惊讶。于是在使用ChatGPT有一周左右后,分享一下用它写程序的效果如何。1、对于矩阵,把减法操作转换加法?感觉不错的,能清晰介绍原理,然后写示例程…...
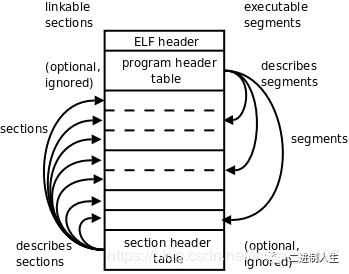
编译链接实战(9)elf符号表
文章目录符号的概念符号表探索前面介绍了elf文件的两种视图,以及两种视图的各自几个组成部分:elf文件有两种视图,链接视图和执行视图。在链接视图里,elf文件被划分成了elf 头、节头表、若干的节(section)&a…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

学习一下用鸿蒙DevEco Studio HarmonyOS5实现百度地图
在鸿蒙(HarmonyOS5)中集成百度地图,可以通过以下步骤和技术方案实现。结合鸿蒙的分布式能力和百度地图的API,可以构建跨设备的定位、导航和地图展示功能。 1. 鸿蒙环境准备 开发工具:下载安装 De…...
