刷题记录:牛客NC20545[HEOI2012]采花
传送门:牛客
题目描述:
题目较长,此处暂略
输入:
5 3 5
1 2 2 3 1
1 5
1 2
2 2
2 3
3 5
输出:
2
0
0
1
0
总结一下题意,就是求区间[l,r][l,r][l,r]出现次数大于1的花的种类数.
考虑使用主席树或者离线树状数组的方法来解决.由于数据加强的原因,导致主席树在本题中是不能完美通过的,洛谷上可以得133分(T了两个点),在牛客上可以过一般数据(MLE+T).因为牛客上的空间甚至只有可怜的256MB,导致我们的主席树在牛客上被卡的死死的.虽然但是,主席树的解法还是可以了解一下的.
首先是主席树解法:
考虑用last1[i]last1[i]last1[i]来记录每一个位置的花上一次出现的位置,那么对于本题来说,我们需要记录区间内出现次数大于1,这就意味着花上一次出现的位置要在我们的区间[l,r][l,r][l,r]里面就可以了.所以此时需要计算的是就是:∑lr(last1[i]>=l)\sum_{l}^r{(last1[i]>=l)}l∑r(last1[i]>=l)为主席树可以解决的经典题目之一.
当然此时就有人要有疑问了,上面的解法显然是有一个问题的,就是我们区间里的花的种类是可能重复的,也就是当我们区间里有三朵同样的花时,此时我们直接使用上述last1last1last1会发现会被重复计算一次.那我们要怎么解决这个问题呢,我们可以在第三朵相同的花出现的时候将前一朵花的贡献删除掉.也就是意味着当我们的第三朵花在区间里面时,前面的花的贡献因为重复了所以可以直接删除掉.
因为对于我们的主席树来说,我们最终的答案是有首尾两个相减得到的,所以我们只在末尾出更改只影响到了包括这三朵花的区间,而对于这样的区间来说,此时显然我们只需要第三朵花的贡献即可.对于不完全包括这三朵花的区间,我们发现要么此前的花本身就没有贡献,删掉也无所谓;要么三朵花都没有贡献,所以删掉不影响这些区间,所以这么做就巧妙的解决了这个问题.
在搞清楚上述关键点之后,直接使用主席树来解决即可:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 2000100
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
struct PerSegment_tree{int sum,lnum,rnum;
}tree[maxn<<5];int cnt=0;int RT[maxn];
int build(int l,int r) {int p=++cnt;tree[p].sum=0;if(l==r) {return p;}int mid=(l+r)>>1;tree[p].lnum=build(l,mid);tree[p].rnum=build(mid+1,r);return p;
}
int update(int per,int l,int r,int pos,int val) {if(pos==0) return per;int p=++cnt;tree[p]=tree[per];tree[p].sum+=val;if(l==r) return p;int mid=(l+r)>>1;if(pos<=mid) tree[p].lnum=update(tree[per].lnum,l,mid,pos,val);else tree[p].rnum=update(tree[per].rnum,mid+1,r,pos,val);return p;
}
int query(int per,int now,int l,int r,int k) {if(l==r) return tree[now].sum-tree[per].sum;int mid=(l+r)>>1;if(k>mid) {return query(tree[per].rnum,tree[now].rnum,mid+1,r,k);}else {int s=tree[tree[now].rnum].sum-tree[tree[per].rnum].sum;return s+query(tree[per].lnum,tree[now].lnum,l,mid,k); }
}
int a[maxn];
int n,c,m;int last1[maxn],last2[maxn];
int main() {n=read();c=read();m=read();RT[0]=build(1,c);for(int i=1;i<=n;i++) {a[i]=read();RT[i]=update(RT[i-1],1,c,last1[a[i]],-1);RT[i]=update(RT[i],1,c,last2[a[i]],1);last1[a[i]]=last2[a[i]];last2[a[i]]=i;}for(int i=1;i<=m;i++) {int l=read(),r=read();printf("%d\n",query(RT[l-1],RT[r],1,c,l));}return 0;
}
方法二:离线树状数组
我们可以将所有的询问区间进行一个排序(按区间右端点从小到大排).那么此时我们的关注点就是所有小于当前区间的右端点的花了.
对于所有小于当前区间右端点的花来说,假设此时我们先后出现了两朵颜色相同的花,此时我们需要将第一朵加入我们的贡献.因为只有当我们的两朵都在区间内的时候,我们此时才有贡献,所以算倒数第二朵的.假设我们此时先后出现了三朵颜色相同的花,注意,此时无论我们的左端点时如何,显然我们应该删除第一朵花原本的贡献,因为无论我们的左端点所在的情况如何,越靠近右端点的花显然是越有可能贡献的(这个可以仔细理解一下).
并且因为我们保证了越靠近后面的花的贡献,所以此时我们的询问区间从小到大排的正确性也就是可以保证了.
讲一讲离线做法的精华所在:直接做这道题是不好做的,但是假设此时我们改变一下此题,假设我们此时的问题是计算区间[l,n][l,n][l,n]的花的贡献,我们是不是就可以使用上面的方法来做了,但是此时我们一旦使用了上面的方法,那么对于nnn之前的所有区间就会产生影响.因为我们删除了前面的花的贡献.但是此时我们进行排序了,就保证后面区间都是在当前区间后面的,对于后面的区间来说,假设这区间的左端点在我们当前区间左端点的左边,那么没关系,因为当前区间左端点的贡献已经记录在区间里了.假设这区间的左端点在当前区间左端点右边,那么也没关系
然后使用树状数组解决即可:
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define root 1,n,1
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
inline ll read() {ll x=0,w=1;char ch=getchar();for(;ch>'9'||ch<'0';ch=getchar()) if(ch=='-') w=-1;for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0';return x*w;
}
#define maxn 2001000
const double eps=1e-8;
#define int_INF 0x3f3f3f3f
#define ll_INF 0x3f3f3f3f3f3f3f3f
inline int lowbit(int x) {return x&(~x+1);
}
int tree[maxn];int n,m,c;int a[maxn];
void Add(int pos,int val) {while(pos<=n) {tree[pos]+=val;pos+=lowbit(pos);}
}
int query(int pos) {int ans=0;while(pos) {ans+=tree[pos];pos-=lowbit(pos);}return ans;
}
struct Ask{int l,r,id;
}ask[maxn];
bool cmp(Ask aa,Ask bb) {return aa.r<bb.r;
}
int last1[maxn];int last2[maxn];int ans[maxn];
int main() {n=read();c=read();m=read();for(int i=1;i<=n;i++) {a[i]=read();}for(int i=1;i<=m;i++) {ask[i].l=read();ask[i].r=read();ask[i].id=i;}sort(ask+1,ask+m+1,cmp);int pos=1;for(int i=1;i<=m;i++) {while(pos<=n&&pos<=ask[i].r) {if(last1[a[pos]]==0) {last1[a[pos]]=pos;}else {if(last2[a[pos]]==0) {Add(last1[a[pos]],1);last2[a[pos]]=pos;}else {Add(last1[a[pos]],-1);Add(last2[a[pos]],1);last1[a[pos]]=last2[a[pos]];last2[a[pos]]=pos;}}pos++;}ans[ask[i].id]=query(ask[i].r)-query(ask[i].l-1);}for(int i=1;i<=m;i++) {printf("%d\n",ans[i]);}return 0;
}
相关文章:

刷题记录:牛客NC20545[HEOI2012]采花
传送门:牛客 题目描述: 题目较长,此处暂略 输入: 5 3 5 1 2 2 3 1 1 5 1 2 2 2 2 3 3 5 输出: 2 0 0 1 0总结一下题意,就是求区间[l,r][l,r][l,r]出现次数大于1的花的种类数. 考虑使用主席树或者离线树状数组的方法来解决.由于数据加强的原因,导致主席树在本题中是不能完美通…...

每日学术速递2.21
CV - 计算机视觉 | ML - 机器学习 | RL - 强化学习 | NLP 自然语言处理 Subjects: cs.CV 1.T2I-Adapter: Learning Adapters to Dig out More Controllable Ability for Text-to-Image Diffusion Models 标题:T2I-Adapter:学习Adapter,为…...
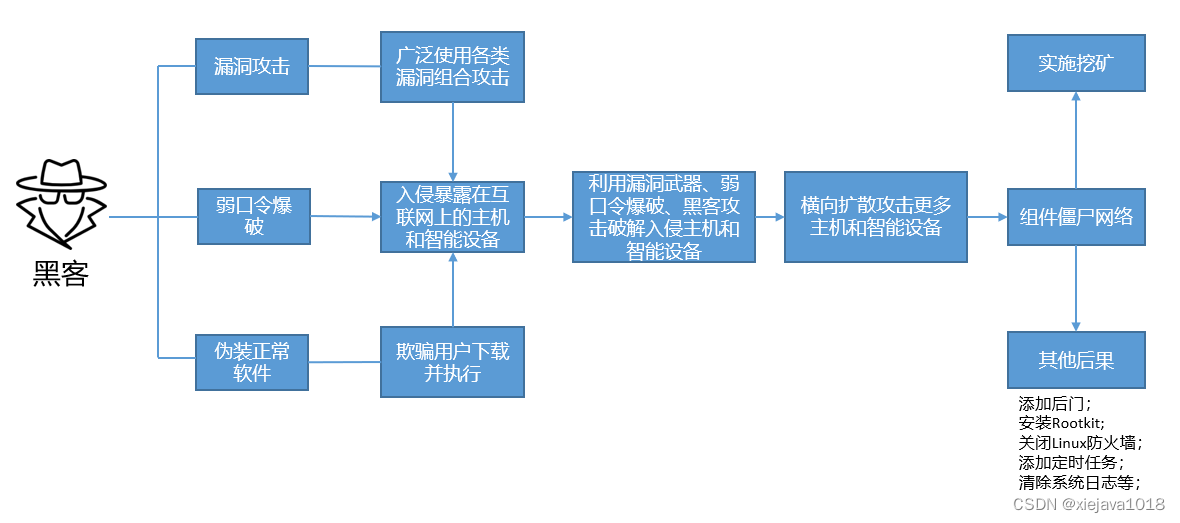
网络安全之认识挖矿木马
一、什么是挖矿木马? 比特币是以区块链技术为基础的虚拟加密货币,比特币具有匿名性和难以追踪的特点,经过十余年的发展,已成为网络黑产最爱使用的交易媒介。大多数勒索病毒在加密受害者数据后,会勒索代价高昂的比特币…...
OpenCV实战——基于分水岭算法的图像分割
OpenCV实战——基于分水岭算法的图像分割0. 前言1. 分水岭算法2. 分水岭算法直观理解3. 完整代码相关链接0. 前言 分水岭变换是一种流行的图像处理算法,用于快速将图像分割成同质区域。分水岭变换主要基于以下思想:当图像被视为拓扑浮雕时,均…...

YOLOv8模型调试记录
前言 新年伊始,ultralytics 公司在 2023 年 1月 10 号开源的 YOLOv5 的下一个重大更新版本,目前支持图像分类、物体检测和实例分割任务,在还没有开源时就收到了用户的广泛关注。 值得一提的是,在博主的印象中,YOLO系…...

算法刷题打卡第97天:删除字符串两端相同字符后的最短长度
删除字符串两端相同字符后的最短长度 难度:中等 给你一个只包含字符 a,b 和 c 的字符串 s ,你可以执行下面这个操作(5 个步骤)任意次: 选择字符串 s 一个 非空 的前缀,这个前缀的所有字符都相…...
---使用IndexBuffer(索引缓冲区))
WebGPU学习(3)---使用IndexBuffer(索引缓冲区)
现在让我们将 IndexBuffer 与 VertexBuffer 一起使用。演示示例 1.准备索引数据 我们用 Uint16Array 类型来准备索引数据。我们将矩形的4个点放到 VertexBuffer 中,然后根据三角形绘制顺序,组织成 0–1–2 和 0–2–3 的结构。 const quadIndexArray …...

Java代码加密混淆工具有哪些?
在Java中,代码加密混淆工具可以帮助开发者将源代码进行加密和混淆处理,以增加代码的安全性和保护知识产权。以下是一些流行的Java代码加密混淆工具: 第一款:ProGuard:ProGuard ProGuard:ProGuard…...
 | 机试题+算法思路+考点+代码解析 【2023】)
华为OD机试 - 高效的任务规划(Python) | 机试题+算法思路+考点+代码解析 【2023】
高效的任务规划 题目 你有 n 台机器编号为1-n,每台都需要完成一项工作, 机器经过配置后都能独立完成一项工作。 假设第i台机器你需要花 Bi 分钟进行设置, 然后开始运行,Ji分钟后完成任务。 现在,你需要选择布置工作的顺序,使得用最短的时间完成所有工作。 注意,不能同…...

ChatGPT写程序如何?
前言ChatGPT最近挺火的,据说还能写程序,感到有些惊讶。于是在使用ChatGPT有一周左右后,分享一下用它写程序的效果如何。1、对于矩阵,把减法操作转换加法?感觉不错的,能清晰介绍原理,然后写示例程…...
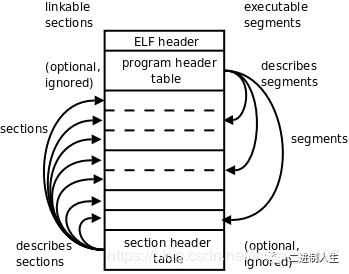
编译链接实战(9)elf符号表
文章目录符号的概念符号表探索前面介绍了elf文件的两种视图,以及两种视图的各自几个组成部分:elf文件有两种视图,链接视图和执行视图。在链接视图里,elf文件被划分成了elf 头、节头表、若干的节(section)&a…...

React合成事件的原理是什么
事件介绍 什么是事件? 事件是在编程时系统内发生的动作或者发生的事情,而开发者可以某种方式对事件做出回应,而这里有几个先决条件 事件对象 给事件对象注册事件,当事件被触发后需要做什么 事件触发 举个例子 在机场等待检票…...
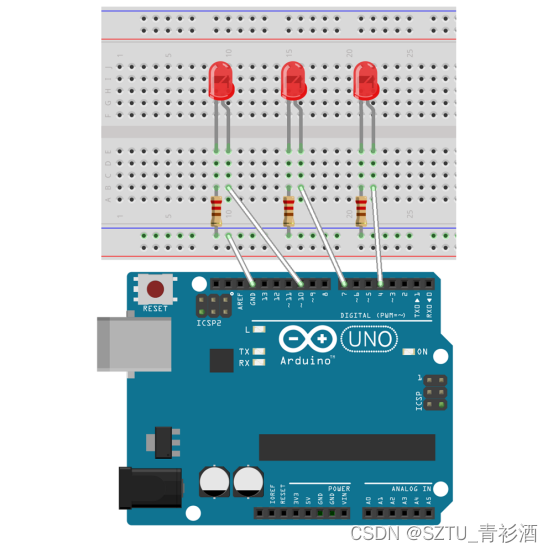
Arduino-交通灯
LED交通灯实验实验器件:■ 红色LED灯:1 个■ 黄色LED灯:1 个■ 绿色LED灯:1 个■ 220欧电阻:3 个■ 面包板:1 个■ 多彩杜邦线:若干实验连线1.将3个发光二极管插入面包板,2.用杜邦线…...
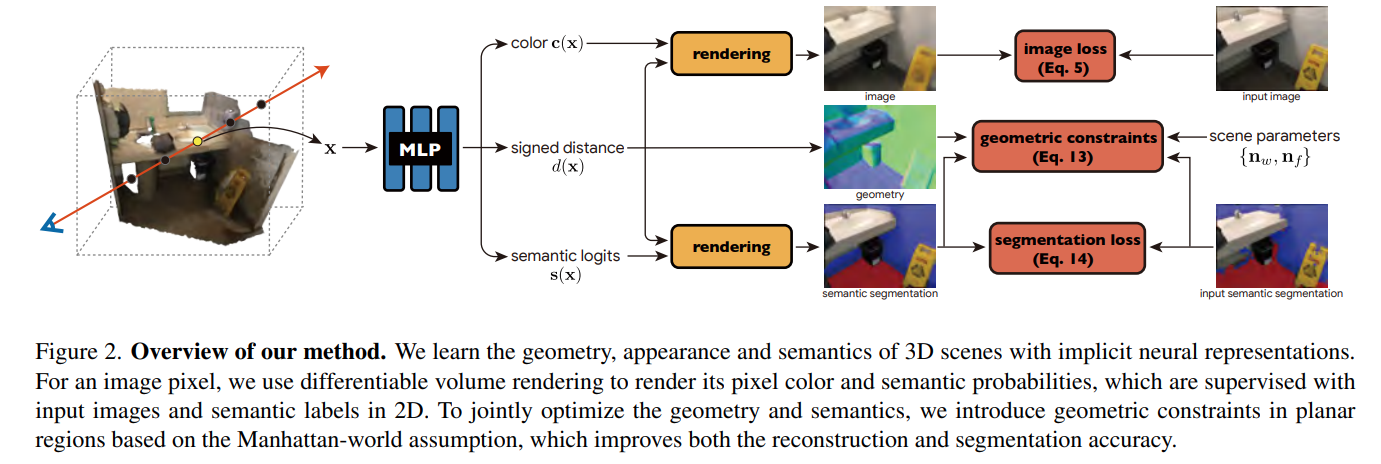
【论文笔记】Manhattan-SDF == ZJU == CVPR‘2022 Oral
Neural 3D Scene Reconstruction with the Manhattan-world Assumption 本文工作:基于曼哈顿世界假设,重建室内场景三维模型。 1.1 曼哈顿世界假设 参考阅读文献:Structure-SLAM: Low-Drift Monocular SLAM in Indoor EnvironmentsIEEE IR…...
好消息!Ellab(易来博)官方微信公众号开通了!携虹科提供专业验证和监测解决方案
自1949年以来,丹麦Ellab一直通过全球范围内的验证和监测解决方案,协助全球生命科学和食品公司优化和改进其流程的质量。Ellab全面的无线数据记录仪,热电偶系统,无线环境监测系统,校准设备,软件解决方案等等…...
想要去字节跳动面试Android岗,给你这些面试知识点
关于面试字节跳动,我总结一些面试点,希望可以帮到更多的小伙伴,由于篇幅问题这里没有把全部的面试知识点问题都放上来!!目录:1.网络2.Java 基础&容器&同步&设计模式3.Java 虚拟机&内存结构…...

Java的Lambda表达式的使用
Lambda表达式是Java 8中引入的一个重要特性,它是一种简洁而强大的语法结构,可以用于替代传统的匿名内部类。 Lambda表达式的语法结构如下: (parameters) -> expression或者 (parameters) -> { statements; }其中,paramet…...
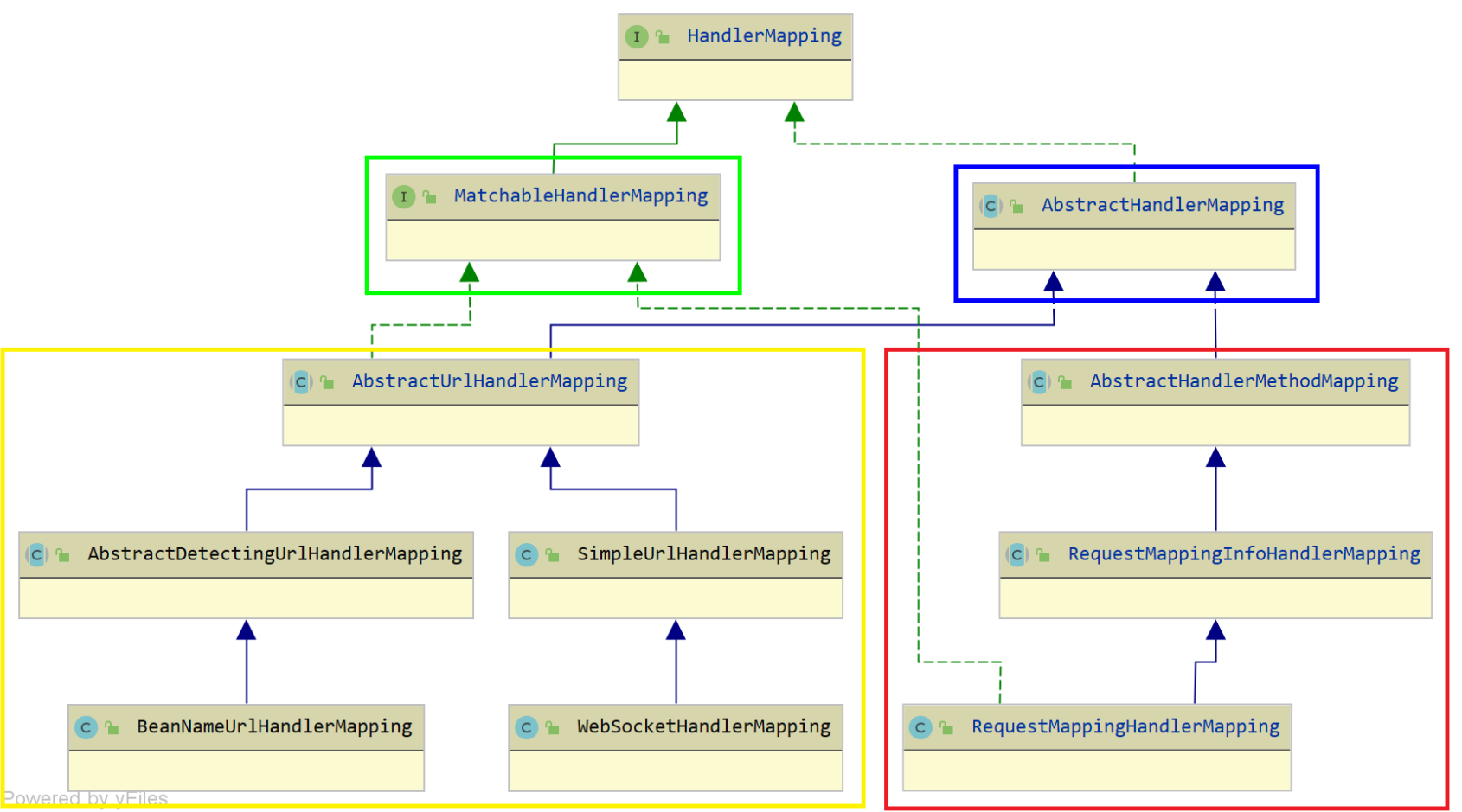
Spring MVC 源码 - HandlerMapping 组件(三)之 AbstractHandlerMethodMapping
HandlerMapping 组件HandlerMapping 组件,请求的处理器匹配器,负责为请求找到合适的 HandlerExecutionChain 处理器执行链,包含处理器(handler)和拦截器们(interceptors)handler 处理器是 Objec…...

超店有数,为什么商家要使用tiktok达人进行营销推广呢?
近几年互联网发展萌生出更多的短视频平台,而tittok这个平台在海外也越来越火爆。与此同时,很多商家也开始用tiktok进行营销推广。商家使用较多的方式就是达人营销,这种方法很常见且转化效果不错。那为什么现在这么多商家喜欢用tiktok达人进行…...

【分享】订阅万里牛集简云连接器同步企业采购审批至万里牛系统
方案场景 面临着数字化转型的到来,不少公司希望实现业务自动化需求,公司内部将钉钉作为办公系统,万里牛作为ERP系统,两个系统之前的数据都储存在各自的后台,导致数据割裂,数据互不相通,人工手动…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...
