C语言之练习题

欢迎来到我的世界
希望这篇文章对你有所帮助,有不足的地方还请指正,大家一起学习交流 !
目录
- 前言
- 编程题
- 第一题:珠玑妙算
- 第二题:寻找奇数
- 第三题:寻找峰值
- 第四题:数对
- 总结
前言
这是暑假题目的收尾文章,我的暑假作业一共写了四篇文章,本篇文章有四篇编程题,我很喜欢四这个数字,感谢铁子们的支持,新的篇章即将来到。😎

编程题
第一题:珠玑妙算
地址:oj地址

解题思路:
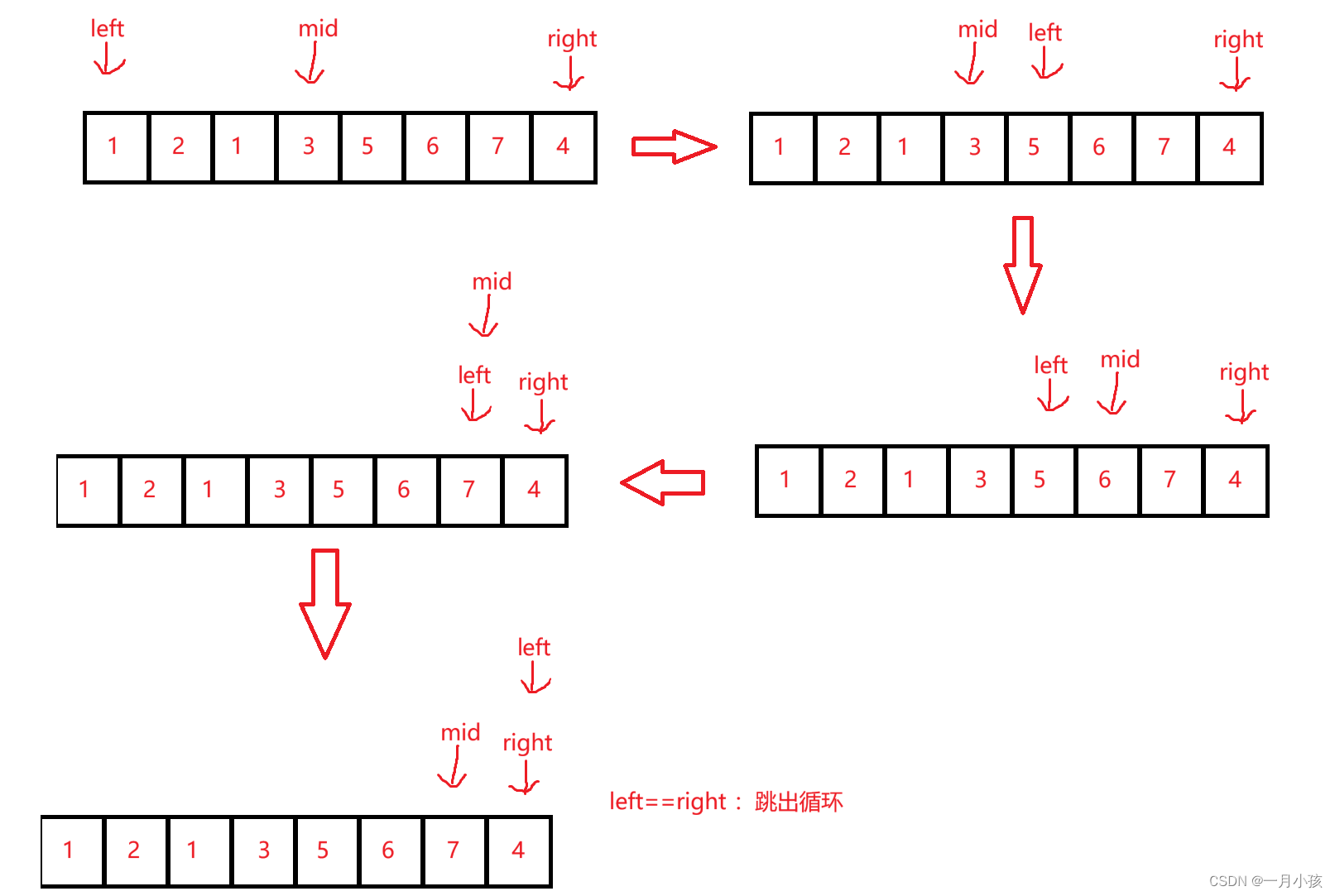
暴力求解:分别记录猜中的个数和伪猜中的个数存入数组相应位置。
- 猜中的个数好记录,直接让颜色组合的数组与猜测的数组进行一一比较,如果相等,那猜中的个数++;
- 伪猜中的个数进行两次遍历;第一次遍历颜色组合的数组,在让该数组中的元素都遍历一遍猜测数组元素,如果相等伪猜中个数++,注意:并将猜测数组该位置赋值为空格
' '这是为了确定唯一性;
注意:这里伪猜中的个数包含了猜中的个数,所以在存入数组的是(伪猜中的个数-猜中的个数);
代码实现:
int* masterMind(char* solution, char* guess, int* returnSize) {*returnSize = 2;//只用两个元素,分别记录猜中个数和伪猜中个数int* arr = (int*)malloc(sizeof(int) * (*returnSize));int i = 0;int sum = 0;//猜中的个数for (i = 0; i < 4; i++){if (solution[i] == guess[i]){sum++;}}arr[0] = sum;int count = 0;//记录违猜中的个数int j = 0;for (i = 0; i < 4; i++){for (j = 0; j < 4; j++){if (solution[i] == guess[j] )//找到相等的,且将猜测数组中的值该成空格;{count++;guess[j] = ' ';break;}}}arr[1] = count - arr[0];return arr;
}第二题:寻找奇数
地址:oj地址
解题思路:
这道题其实也叫做:寻找单身狗
考察的是对按位异或^的深刻了解:我们首先来了解下
^他的运算原则是:相同为0,相异位1;
在来看到:一个数^他相同数结果为0;
假如一个数3:二进制码:011;
当3 ^ 3 = 0所以:3 ^ 0 = 3;
结论:0 ^任何数都 = 该数本身,任何数^该数本身=0;所以我们可以利用这一特性:
题目中说输入一个数组,该数组只有唯一的一个单着的;
所以让0按位异或^上该数组所有数就可以找出那个单着的数;
就像单身狗一样,无所遁形😎
代码实现:
int main() {int n=0;scanf("%d",&n);int i=0;int arr=0;int m=0;//m^上该数组所有元素for(i=0;i<n;i++){scanf("%d",&arr);m^=arr;}printf("%d",m);return 0;
}
第三题:寻找峰值
地址:oj地址
第一个解题思路:暴力求解
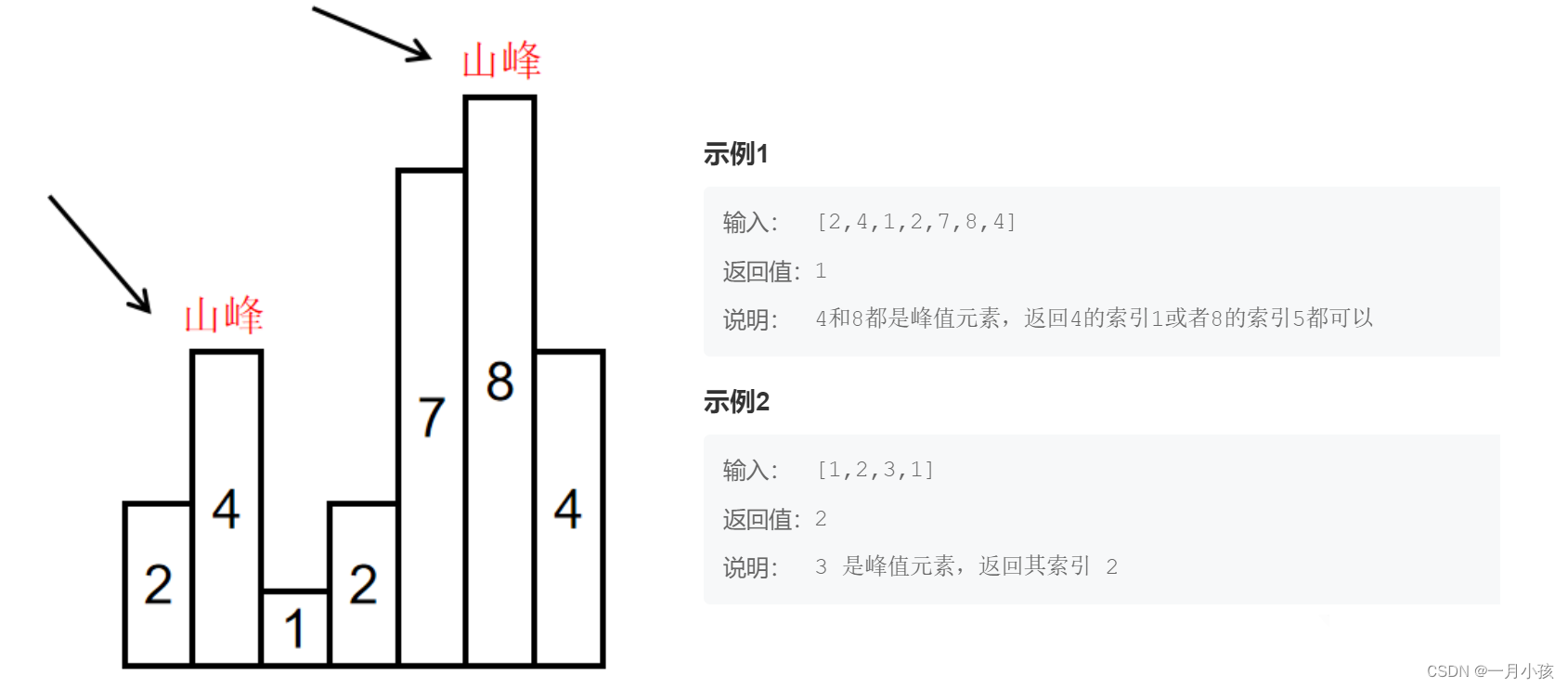
根据在数组范围内,只要一个数严格大于两侧的数就为峰值,对nums数组进行遍历,找到一个峰值即可;
暴力求解,代码实现:
int findPeakElement(int* nums, int numsLen ) {// write code hereint i=0;if(numsLen==1)//若只有一个值,其本身就是峰值return 0;if(nums[0]>nums[1])//若峰值为第一个元素,单独讨论return 0;if(nums[numsLen-1]>nums[numsLen-2])//若峰值为最后一个元素,单独讨论return numsLen-1;for(i=1;i<numsLen-1;i++)//遍历[1,numsLen-1)范围{if(nums[i]>nums[i-1] && nums[i]>nums[i+1])//找到峰值{return i;}}return 0;//若还是找不到峰值,就返回0;
}
第二个解题思路:二分思想
在首元素和最后一个为峰值都要单独考虑;
二分思想:设置三个指针left,right,找到中间位置的值mid,然后根据mid和其两边的值的进行比较,哪边要大于mid值就往那边找峰值,直到mid值严格大于其两边的值;
- 如果
nums[mid]<nums[mid+1],那么意味这峰值位于mid右边,根据二分查找的思想,让left=mid+1;- 若
nums[mid]>=nums[mid+1],那就意味着峰值位于mid的左边;根据二分查找的思想,让right=mid;- 注意
mid的值:mid = left + (right - left) / 2;-
二分求解,代码实现:
int findPeakElement(int* nums, int numsLen ) {// write code hereif (numsLen == 1 || nums[0] > nums[1]) return 0;if (nums[numsLen - 1] > nums[numsLen - 2]) return numsLen - 1;int left = 0, right = numsLen - 1, mid;while (left < right) {mid = left + (right - left) / 2;if (nums[mid] < nums[mid+1])//中间比右边小,意味着右边肯定有个峰值left = mid + 1;else //否则在左边包括当前位置肯定有个峰值right = mid;}return right;
}
第四题:数对
地址:oj地址

第一个解题思路:暴力求解
暴力求解:将
x和y分别遍历[1, n],进行判断当x % y >= k时统计计数count++即可,但是这样的话当 n 的值非常大的时候循环次数将非常恐怖,需要循环n^2次;
注意:这个方法会运行超时;
代码实现:
#include <stdio.h>int main() {int i=0;int j=0;int n,k;long count=0;scanf("%d%d",&n,&k);for(i=1;i<=n;i++){for(j=1;j<=n;j++){if((i%j)>=2){count++;}}}printf("%ld",count);return 0;
}
第二个解题思路:
要理解数学公式:
((n/y)*(y-k))+((n%y<k)?0:(n%y-k+1));
假如n=10,k=3;
当y <=k时,意味着任何数字取模y的结果都在[0, k-1]之间,都是不符合条件的。
当y=k+1=4,x 符合条件的数字有 3,7;
当y=k+2=5,x 符合条件的数字有 3,4,8,9;所以当
y=k+n:
x小于y当前值,且符合条件的数字数量是:y-k个;
x大于y当前值,小于2*y的数据中,且符合条件的数字数量是:y-k个;
可以能看出来,在y的整数倍区间内,x符合条件的数量就是(n / y) * (y - k)个;
n / y表示有多少个完整的0 ~ y区间,y - k表示有每个区间内有多少个符合条件的数字;
最后还要考虑的是6...往后这种超出倍数区间超过n的部分的统计
n % y就是多出完整区间部分的数字个数,其中k以下的不用考虑,
则符合条件的是n % y - (k-1)个。
这里需要注意的是类似于9这种超出完整区间的数字个数 本就小于k的情况,则为0
最终公式:(n / y) * (y - k) + ((n % y < k) ? 0, (n % y - k + 1));
代码实现:
#include <stdio.h>int main() {long n,k;scanf("%ld%ld",&n,&k);if(k==0){printf("%ld",n*n);return 0;}long count=0;for(long y=k+1;y<=n;y++){count+=((n/y)*(y-k))+((n%y<k)?0:(n%y-k+1));}printf("%ld",count);return 0;
}
总结
到了最后:感谢支持
我还想告诉你的是:
------------对过程全力以赴,对结果淡然处之
也是对我自己讲的
相关文章:

C语言之练习题
欢迎来到我的世界 希望这篇文章对你有所帮助,有不足的地方还请指正,大家一起学习交流 ! 目录 前言编程题第一题:珠玑妙算第二题:寻找奇数第三题:寻找峰值第四题:数对 总结 前言 这是暑假题目的收尾文章&am…...
没钱,没人,没经验?传统制造型企业如何用无代码实现转型
2023年,国家市场监督管理总局发布了三项重要标准,包括《工业互联网平台选型要求》、《工业互联网平台微服务参考框架》和《工业互联网平台开放应用编程接口功能要求》。这些标准的发布对于完善工业互联网平台标准体系,提升多样化工业互联网平…...

CentOS ARM 部署 kubernetes v1.24.6
1.背景 之前安装的kubernetes版本为v1.19.0 树莓派使用(CentOS7.9 armv71 Kubernetes1.19.0), 由于版本过低,一些HPA相关的功能支持不是特别好,因此需要将版本升级,本次会将版本升级为v1.24.6. 2. 如何upgrade 2.1. 优雅升级 kubeadm自带…...

LeetCode 725. Split Linked List in Parts【链表】中等
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...

云计算中的负载均衡技术,确保资源的平衡分配
文章目录 1. 硬件负载均衡器2. 软件负载均衡器3. DNS负载均衡4. 内容分发网络(CDN) 🎈个人主页:程序员 小侯 🎐CSDN新晋作者 🎉欢迎 👍点赞✍评论⭐收藏 ✨收录专栏:云计算 ✨文章内…...

探索 SOCKS5 代理在跨境电商中的网络安全应用
随着全球化的发展,跨境电商成为了商业界的一颗新星,为企业提供了无限的发展机遇。然而,随之而来的是网络安全的挑战,特别是在处理国际网络流量时。在这篇文章中,我们将探讨如何利用 SOCKS5 代理和代理 IP 技术来加强跨…...

全网独家:编译CentOS6.10系统的openssl-1.1.1多版本并存的rpm安装包
CentOS6.10系统原生的openssl版本太老,1.0.1e,不能满足一些新版本应用软件的要求,但是它又被wget、mysql-libs、python-2.6.6、yum等一众系统包所依赖,不能再做升级。故需考虑在不影响系统原生openssl的情况下,安装较新…...

【go】异步任务解决方案Asynq实战
文章目录 一.Asynq介绍二.所需工具三.代码示例四.Reference 一.Asynq介绍 Asynq 是一个 Go 库,一个高效的分布式任务队列。 Asynq 工作原理: 客户端(生产者)将任务放入队列服务器(消费者)从队列中拉出任…...

掌握 Android 自动化测试框架 UiAutomator UiAutomator2
掌握 Android 自动化测试框架 UiAutomator & UiAutomator2 一、UiAutomator 简介二、UiAutomator2 的诞生三、UiAutomator2 的应用实践总结你是否曾经在进行 Android 应用开发时,对于如何进行全面、有效的自动化测试感到困惑?你是否想要更高效地进行 UI 测试,而不是一遍…...
)
c#抽象类(abstract)
概述: C#中的抽象类是一种特殊类型的类,它不能被实例化,只能被继承。抽象类用于提供一个共享的基类,其中定义了一些方法和属性的签名,但没有具体的实现。这些方法和属性可以在派生类中进行实现。 使用抽象类的主要目…...
语义分割实践思考记录(个人备忘录)
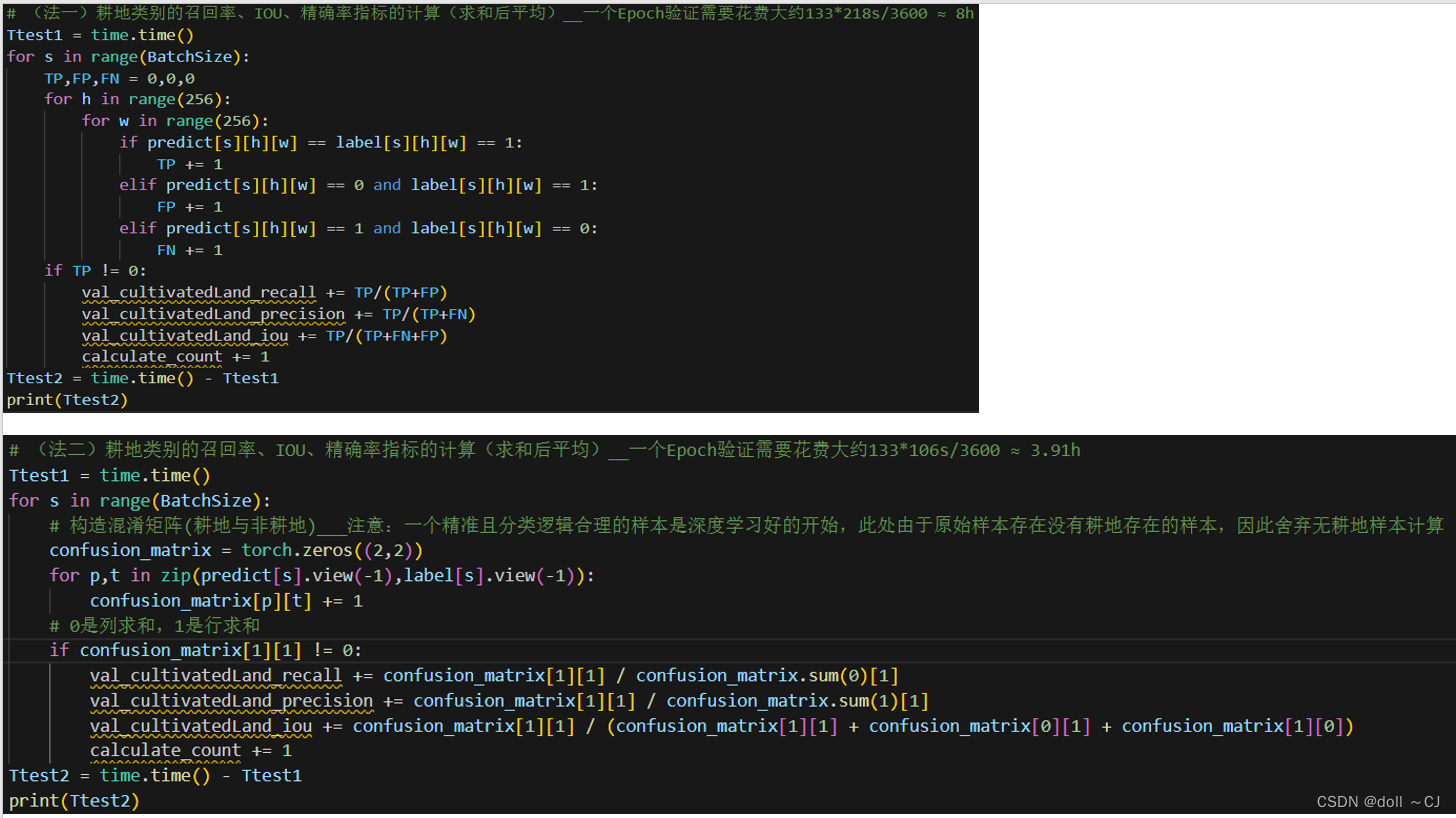
一、任务管理器、NVDIA的GPU利用率显示[1][2] 若需要在任务管理器中查看基于Pytorch框架的GPU利用率,那么,我们需要将监控面板监测内容调整为cuda。图一(左)即为英伟达命令行工具面板。 图一 英伟达GPU使用率监控 二、基于混淆矩阵…...

Zebec Protocol 成非洲利比亚展会合作伙伴,并将向第三世界国家布局
在 9 月 6 日,The Digital Asset Summit ’23(利比亚大会)在尼日利亚首度阿布贾的 NAF 会议中心举办,该会议对 Web3 领域在非洲地区的发展进行了探索,旨在推动非洲地区区块链产业的进一步发展,据悉该会议室…...

随机流-RandomAccessFile
RandomAccessFile RandomAccessFile 基本操作案例 RandomAccessFile 基本操作 案例 import java.io.*;public class TestMain09 {public static void main(String[] args) throws Exception {insert("D:\\home\\product\\aa.txt",2,"ni");}public static…...

单例和静态类
C#中的单例(Singleton)和静态类(Static Class)是两种不同的设计模式,它们各自有不同的用途和特点。 单例模式是一种设计模式,它确保一个类只有一个实例,并提供全局访问点。通常,单例…...

PMP-项目风险管理的重要性
一、什么是项目风险管理 项目风险管理旨在识别和管理未被其他项目管理过程所管理的风险。如果不妥善管理,这些风险有可能导致项目偏离计划,无法达成既定的项目目标。因此,项目风险管理的有效性直接关乎项目成功与否。 每个项目都在两个层面…...

学习的心得
文章目录 第一节课心得**学会了敲写数学公式** 第一节课心得 老师讲得非常好,我们下载了xmind,如何制作思维导图 学会了敲写数学公式 ∫ 10 20 ( x 2 − 3 x 2 ) d x \displaystyle\int_{10}^{20}(x^2-3x2)dx ∫1020(x2−3x2)dx...

Python网络爬虫中这七个li标签下面的属性值,不是固定的,怎样才能拿到他们的值呢?...
点击上方“Python爬虫与数据挖掘”,进行关注 回复“书籍”即可获赠Python从入门到进阶共10本电子书 今 日 鸡 汤 愚以为宫中之事,事无大小,悉以咨之,然后施行,必能裨补阙漏,有所广益。 大家好,我…...
白鲸开源 DataOps 平台加速数据分析和大模型构建
作者 | 李晨 编辑 | Debra Chen 数据准备对于推动有效的自助式分析和数据科学实践至关重要。如今,企业大都知道基于数据的决策是成功数字化转型的关键,但要做出有效的决策,只有可信的数据才能提供帮助,随着数据量和数据源的多样…...
(其他) 剑指 Offer 65. 不用加减乘除做加法 ——【Leetcode每日一题】
❓ 剑指 Offer 65. 不用加减乘除做加法 难度:简单 写一个函数,求两个整数之和,要求在函数体内不得使用 “”、“-”、“*”、“/” 四则运算符号。 示例: 输入: a 1, b 1 输出: 2 提示: a, b 均可能是负数或 0结果不会溢出 …...

RestTemplate 的用法
1.引入对应依赖 2.private final RestTemplate restTemplate; 3.上代码 Service Slf4j public class CspWarehouseServiceImpl implements ICspWarehouseService { private final RestTemplate restTemplate;public CspWarehouseServiceImpl() {this.restTemplate new Rest…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...