算法通关村第十七关:青铜挑战-贪心其实很简单
青铜挑战-贪心其实很简单
1. 难以解释的贪心算法
贪心学习法则:直接做题,不考虑贪不贪心
贪心(贪婪)算法
是指在问题尽心求解时,在每一步选择中都采取最好或者最优(最有利)的选择,从而希望能够导致结果最好或者最优的算法
贪心算法所得到的结果不一定是最优的结果,但是都是相对近似最优解的结果
怎么知道什么时候改用贪心呢?
要求要解决的问题具有“最优子结构”
贪心怎么学?
将常见的贪心题都找出来看看大致是什么样子的,学一学就行了
贪心常见的应用场景?
- 排序问题:选择排序、拓扑排序
- 优先队列:堆排序
- 赫夫曼压缩编码
- 图里的 Prim、Fruska和Dijkstra算法
- 硬币找零问题
- 分数背包问题
- 并查集的按大小或者高度合并问题,或者排名
- 任务调度部分场景
- 一些复杂的近似算法
2. 贪心问题举例
2.1 分发饼干
LeetCode 455
https://leetcode.cn/problems/assign-cookies/
思路分析
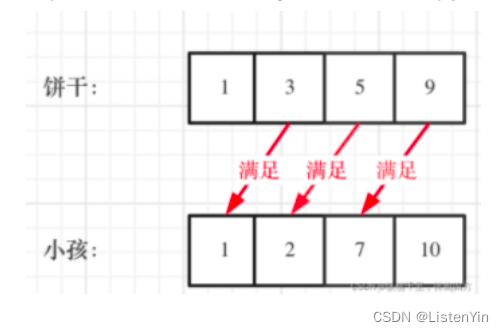
既要满足小孩的胃口,也不要造成饼干的浪费;
大饼干既可以满足胃口大的孩子,也可以满足胃口小的孩子,就应该优先满足胃口大的;
局部最优:大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个
全局最优:喂饱尽可能多的孩子
贪心策略:考虑胃口,大饼干先喂饱大胃口,最后看能满足几个孩子的需要
- 先将饼干数组和小孩数组排序
- 然后从后向前比那里小孩数组,用大饼干优先满足胃口大的,并统计满足孩子的数量
代码实现
class Solution:def findContentChildren(self, g: List[int], s: List[int]) -> int:g.sort(reverse=True)s.sort(reverse=True)s_len = len(s)s_index = 0count = 0for i in g:if s_index < s_len and i <= s[s_index]:s_index += 1count += 1return count
2.2 柠檬水找零
LeetCode860
https://leetcode.cn/problems/lemonade-change/
思路分析
分析下主要有三种情况
- 给的是5,直接收下
- 给的是10,给出1个5,此时必须要有1个5才行
- 给的是20,优先消耗1个10,再给1个5。如果没有10,给出3个5
局部最优:遇到账单20,优先消耗10,完成本次找零。10只能给20找零,5更万能
代码实现
class Solution:def lemonadeChange(self, bills: List[int]) -> bool:count_5 = 0count_10 = 0for money in bills:if money == 5:count_5 += 1elif money == 10:count_5 -= 1count_10 += 1elif money == 20:if count_10 > 0:count_10 -= 1count_5 -= 1else:count_5 -= 3if count_5 < 0 or count_10 < 0:return Falsereturn True2.3 分发糖果
LeetCode 135
https://leetcode.cn/problems/candy/
思路分析
每个孩子至少一个糖果
相邻孩子评分更高的获得更多的糖果
- 第一轮,从左到右
- 只要右边的比左边的大,就一直加1
- 如果右边比左边小,就设置为1
- 第二轮,从右到左
- 如果左边的比右边的大,在{i+1}的基础上,先加1再赋值给{i}
- 每个位置i,从left[i]和right[i]中选最大就行了
第一轮
下标 0 1 2 3 4 5 6
得分 1 2 2 5 4 3 2
糖果 1 2 1 2 1 1 1第二轮
下标 0 1 2 3 4 5 6
得分 1 2 2 5 4 3 2
糖果 1 2 1 4 3 2 1选取最大
下标 0 1 2 3 4 5 6
得分 1 2 2 5 4 3 2
糖果 1 2 1 4 3 2 1第一轮
下标 0 1 2 3 4
得分 1 3 4 5 2
糖果 1 2 3 4 1第二轮
下标 0 1 2 3 4
得分 1 3 4 5 2
糖果 1 2 3 2 1选取最大
下标 0 1 2 3 4
得分 1 3 4 5 2
糖果 1 2 3 4 1
代码实现
class Solution:def candy(self, ratings: List[int]) -> int:n = len(ratings)candy_list = [0] * ncandy_list[0] = 1 for i in range(1, n):if ratings[i] > ratings[i-1]:candy_list[i] = candy_list[i-1] + 1else:candy_list[i] = 1for i in range(n-2, -1, -1):if ratings[i] > ratings[i+1]:candy_list[i] = max(candy_list[i+1] + 1, candy_list[i])return sum(candy_list)
相关文章:

算法通关村第十七关:青铜挑战-贪心其实很简单
青铜挑战-贪心其实很简单 1. 难以解释的贪心算法 贪心学习法则:直接做题,不考虑贪不贪心 贪心(贪婪)算法 是指在问题尽心求解时,在每一步选择中都采取最好或者最优(最有利)的选择,从而希望能够导致结果最…...
[Vue3 博物馆管理系统] 使用Vue3、Element-plus的Layout 布局构建组图文章
系列文章目录 第一章 定制上中下(顶部菜单、底部区域、中间主区域显示)三层结构首页 第二章 使用Vue3、Element-plus菜单组件构建菜单 第三章 使用Vue3、Element-plus走马灯组件构建轮播图 第四章 使用Vue3、Element-plus tabs组件构建选项卡功能 第五章…...

【LeetCode算法系列题解】第36~40题
CONTENTS LeetCode 36. 有效的数独(中等)LeetCode 37. 解数独(困难)LeetCode 38. 外观数列(中等)LeetCode 39. 组合总和(中等)LeetCode 40. 组合总和 II(中等)…...
java+ssm+mysql电梯管理系统
项目介绍: 使用javassmmysql开发的电梯管理系统,系统包含管理员,监管员、安全员、维保员角色,功能如下: 管理员:系统用户管理(监管员、安全员、维保员);系统公告&#…...

最近读书了吗?林曦老师与你分享来自暄桐课堂的读书方法
近来,大家有在开心读书吗?对于读书,有一个很生动的说法:“无事常读书,一日是四日。若活七十年,便二百八十。”读书帮助我们超越个体生命经验的限制,此时此地的我们,也可借由书本&…...
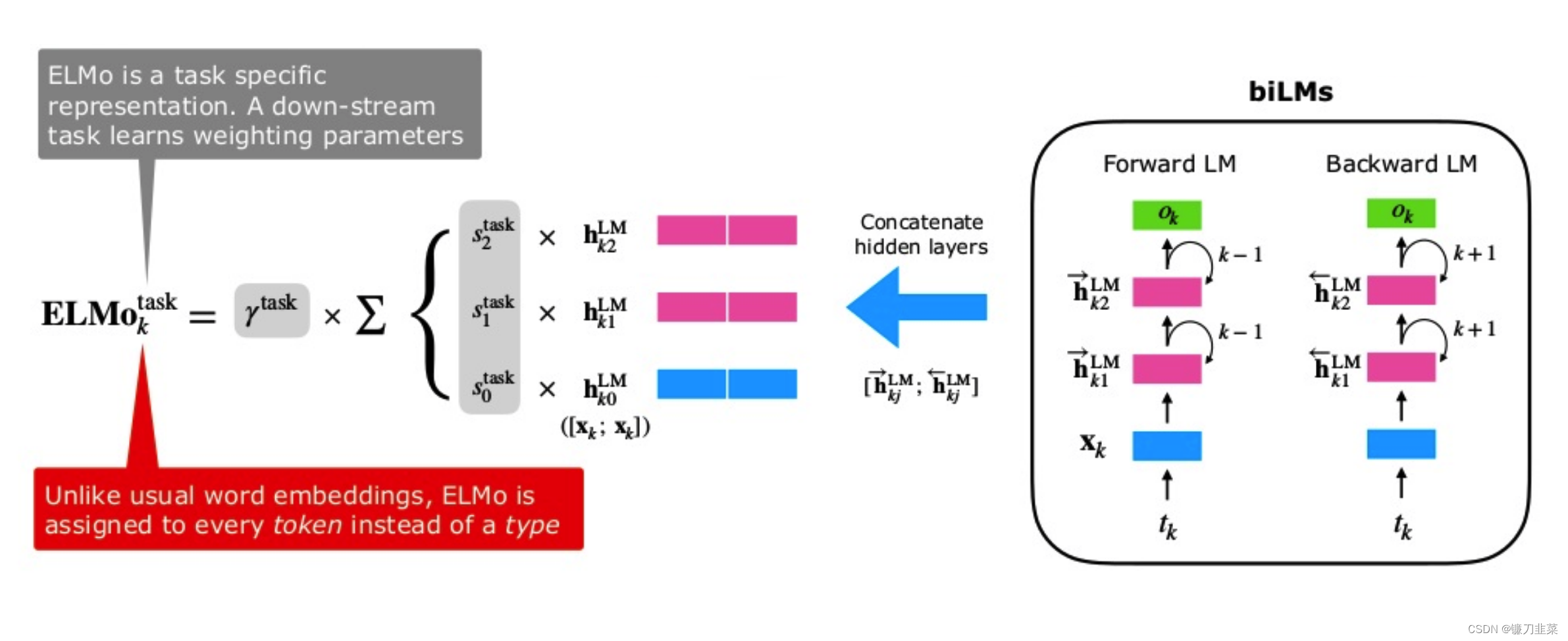
【AI理论学习】语言模型:从Word Embedding到ELMo
语言模型:从Word Embedding到ELMo ELMo原理Bi-LM总结参考资料 本文主要介绍一种建立在LSTM基础上的ELMo预训练模型。2013年的Word2Vec及2014年的GloVe的工作中,每个词对应一个vector,对于多义词无能为力。ELMo的工作对于此,提出了…...

多功能透明屏,在智能家居领域中,有哪些功能特点?显示、连接
多功能透明屏是一种新型的显示技术,它能够在透明的表面上显示图像和视频,并且具有多种功能。 这种屏幕可以应用于各种领域,如商业广告、智能家居、教育等,为用户提供更加便捷和多样化的体验。 首先,多功能透明屏可以…...
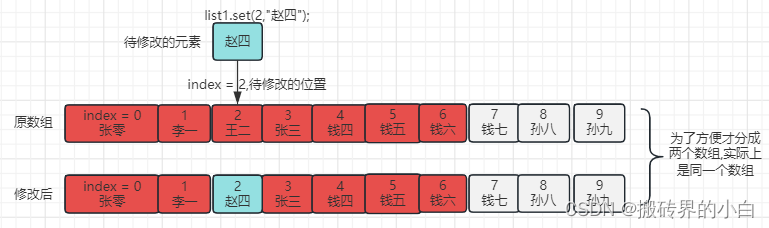
【List篇】ArrayList 详解(含图示说明)
Java中的ArrayList是一个动态数组,可以自动扩展容量以适应数据的添加和删除。它可以用来存储各种类型的数据,例如String,Integer,Boolean等。ArrayList实现了List接口,可以进行常见的List操作,例如添加、插…...

SSL证书只有收费的吗?有没有免费使用的?
首先明白SSL证书是什么SSL英文全称:英文全称: Secure Socket Layer Certificate,中文全称:安全套接字层证书。 SSL是一种由数字证书颁发机构(CA) 签发的数字证书。它用于建立安全的加密连接,确保通过网络传输的数据在客户端和服务器之间的安全性和完整性…...

48V轻混技术
文章目录 48V轻混技术的主要特点和优势48V轻混技术的优缺点优点:缺点: 48V轻混技术的主要特点和优势 48V轻混技术(48V Mild Hybrid Technology)是一种汽车动力系统技术,它结合了内燃机和电动机的优势,以提…...

机器学习基础算法--回归类型和评价分析
目录 1.数据归一化处理 2.数据标准化处理 3.Lasso回归模型 4.岭回归模型 5.评价指标计算 1.数据归一化处理 """ x的归一化的方法还是比较多的我们就选取最为基本的归一化方法 x(x-x_min)/(x_max-x_min) """ import numpy as np from sklea…...

MATLAB 软件功能简介
MATLAB 的名称源自 Matrix Laboratory,1984 年由美国 Mathworks 公司推向市场。 它是一种科学计算软件,专门以矩阵的形式处理数据。MATLAB 将高性能的数值计算和可 视化集成在一起,并提供了大量的内置函数,从而被广泛的应用于科学计算、控制…...
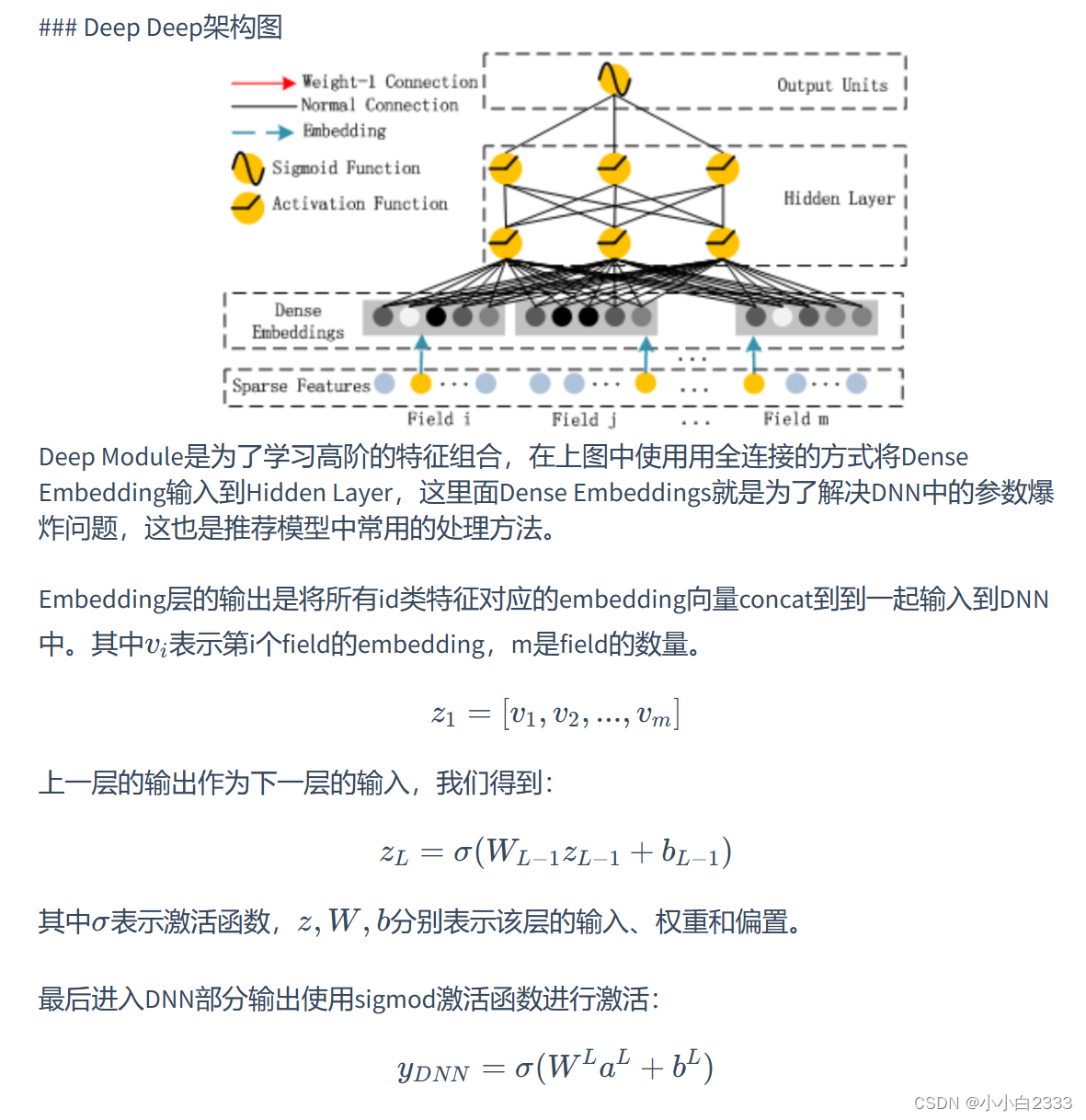
deepfm内容理解
对于CTR问题,被证明的最有效的提升任务表现的策略是特征组合(Feature Interaction); 两个问题: 如何更好地学习特征组合,进而更加精确地描述数据的特点; 如何更高效的学习特征组合。 DNN局限 :当我们使…...
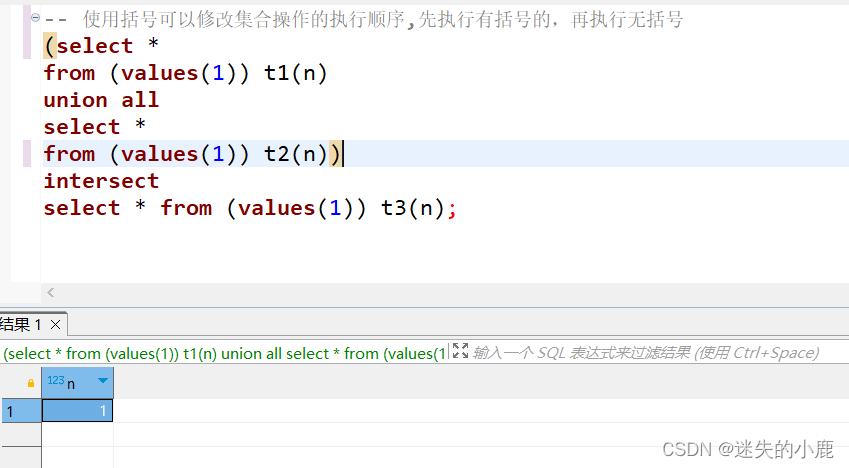
postgresql-集合运算
postgresql-集合运算 并集交集差集集合运算符的优先级 并集 create table excellent_emp( year int not null, emp_id integer not null, constraint pk_excellent_emp primary key(year,emp_id) );insert into excellent_emp values(2018,9); insert into excellent_emp value…...

[持续更新]计算机经典面试题基础篇Day2
[通用]计算机经典面试题基础篇Day2 1、单例模式是什么,线程安全吗 单例模式是一种设计模式,旨在确保一个类只有一个实例,并提供全局访问点。通过使用单例模式,可以避免多次创建相同的对象,节省内存资源,同…...

C++:类和对象(二)
本文主要介绍:构造函数、析构函数、拷贝构造函数、赋值运算符重载、const成员函数、取地址及const取地址操作符重载。 目录 一、类的六个默认成员函数 二、构造函数 1.概念 2.特性 三、析构函数 1.概念 2.特性 四、拷贝构造函数 1.概念 2.特征 五、赋值…...
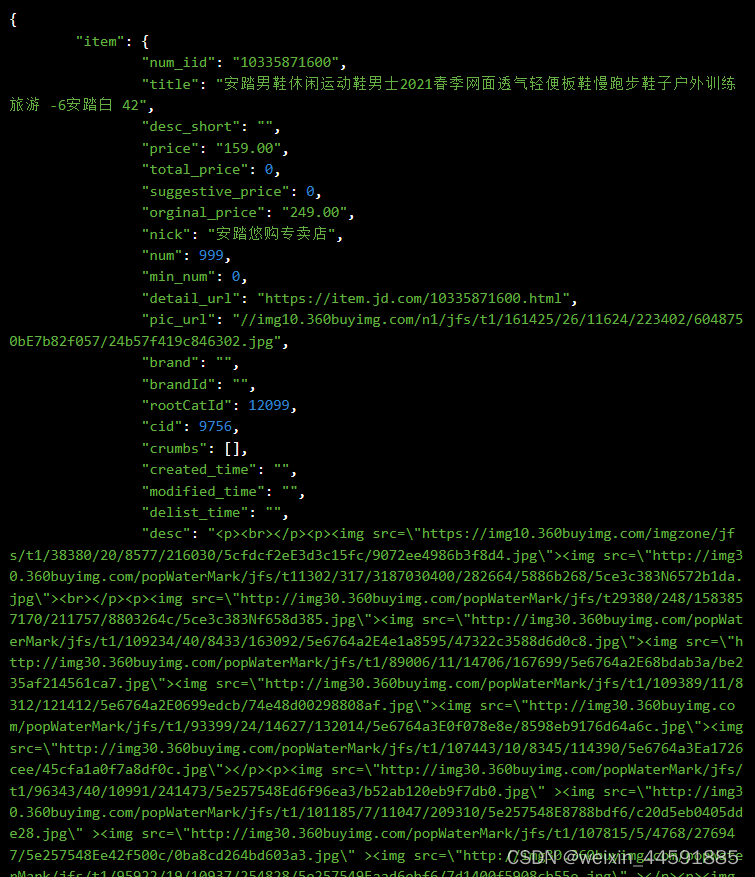
Java“牵手”京东商品详情数据,京东商品详情API接口,京东API接口申请指南
京东平台商品详情接口是开放平台提供的一种API接口,通过调用API接口,开发者可以获取京东商品的标题、价格、库存、月销量、总销量、库存、详情描述、图片等详细信息 。 获取商品详情接口API是一种用于获取电商平台上商品详情数据的接口,通过…...

Fluidd摄像头公网无法正常显示修复一例
Fluidd摄像头在内网正常显示,公网一直无法显示,经过排查发现由于url加了端口号引起的,摄像头url中正常填写的是/webcam?actionsnapshot,或者/webcam?actionstream。但是由于nginx跳转机制,会被301跳转到/webcam/?ac…...
【C++ 学习 ⑳】- 详解二叉搜索树
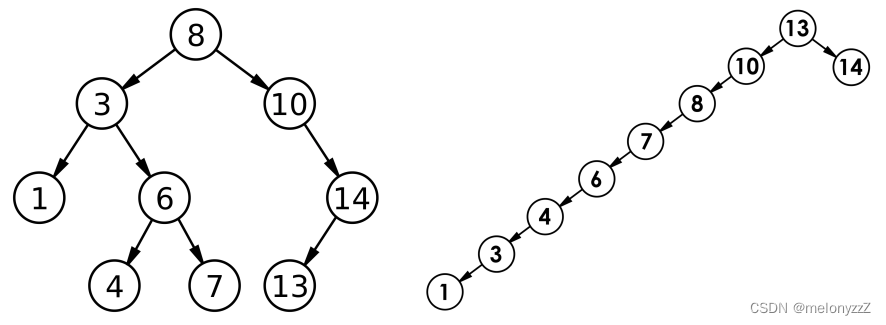
目录 一、概念 二、实现 2.1 - BST.h 2.2 - test.cpp 三、应用 四、性能分析 一、概念 二叉搜索树(BST,Binary Search Tree),又称二叉排序树或二叉查找树。 二叉搜索树是一棵二叉树,可以为空;如果不…...
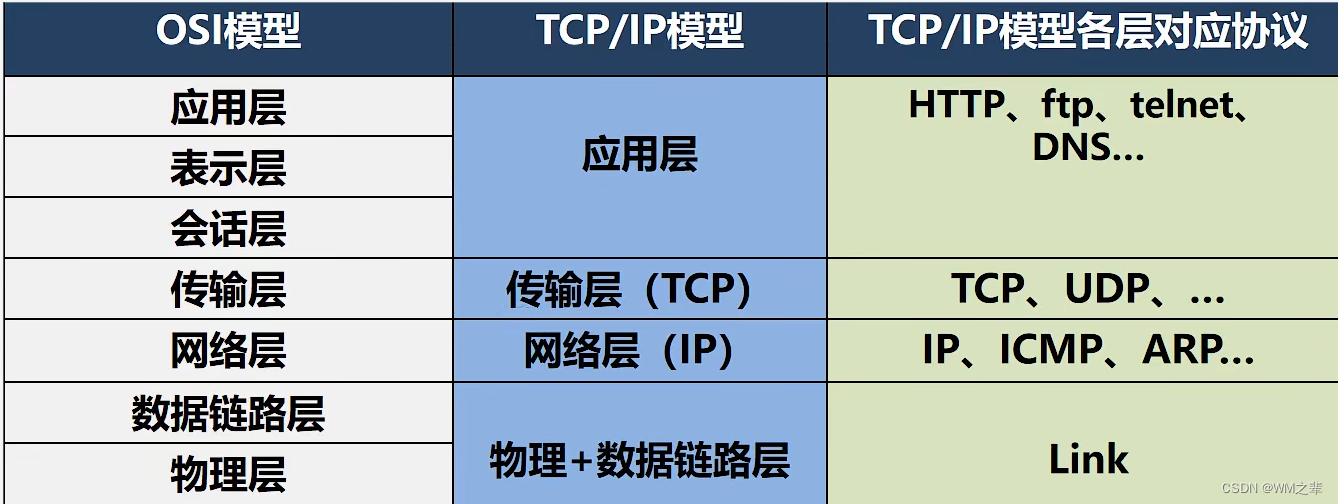
Java中网络的基本介绍。网络通信,网络,ip地址,域名,端口,网络通信协议,TCP/IP传输过程,网络通信协议模型,TCP协议,UDP协议
- 网络通信 概念:网络通信是指通过计算机网络进行信息传输的过程,包括数据传输、语音通话、视频会议等。在网络通信中,数据被分成一系列的数据包,并通过网络传输到目的地。在数据传输过程中,需要确保数据的完整性、准…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...
