【聚类】K-Means聚类
cluster:簇
原理:
这边暂时没有时间具体介绍kmeans聚类的原理。简单来说,就是首先初始化k个簇心;然后计算所有点到簇心的欧式距离,对一个点来说,距离最短就属于那个簇;然后更新不同簇的簇心(簇内所有点的平均值,也就是簇内点的重心);循环往复,直至簇心不变或达到规定的迭代次数
python实现
我们这边通过调用sklearn.cluster中的kmeans方法实现kmeans聚类
入门
原始数据的散点图
from sklearn.cluster import KMeans
import numpy as np
import matplotlib.pyplot as plt# 数据
class1 = 1.5 * np.random.randn(100,2) #100个2维点,标准差1.5正态分布
class2 = 1.5*np.random.randn(100,2) + np.array([5,5])#标准正态分布平移5,5# 画出数据的散点图
plt.figure(0,dpi = 300)
plt.scatter(class1[:,0],class1[:,1],c='y',marker='*')
plt.scatter(class2[:,0],class2[:,1],c='k',marker='.')
plt.axis('off') # 不显示坐标轴
plt.show()

kmeans聚类
#---------------------------kmeans--------------------
# 调用kmeans函数
features = np.vstack((class1,class2))
kmeans = KMeans(n_clusters=2)
kmeans .fit(features)plt.figure(1,dpi = 300)#满足聚类标签条件的行
ndx = np.where(kmeans.labels_==0)
plt.scatter(features[ndx,0],features[ndx,1],c='b',marker='*')ndx = np.where(kmeans.labels_==1)
plt.scatter(features[ndx,0],features[ndx,1],c='r',marker='.')
# 画出簇心
plt.scatter(kmeans.cluster_centers_[:,0],kmeans.cluster_centers_[:,1],c='g',marker='o')plt.axis('off') # 去除画布边框
plt.show()

进一步:选择簇心k的值
前面的数据是我们自己创建的,所以簇心k是我们自己可以定为2。但是在实际中,我们不了解数据,所以我们需要根据数据的情况确定最佳的簇心数k。
这是下面用到的数据data11_2.txt【免费】这是kmean聚类中用到的一个数据资源-CSDN文库
簇内离差平方方和与拐点法(不太好判断)
定义是簇内的点,
是簇的重心。
则所有簇的簇内离差平方和的和为。然后通过可视化的方法,找到拐点,认为突然变化的点就是寻找的目标点,因为继续随着k的增加,聚类效果没有大的变化
借助python中的“md = KMeans(i).fit(b),md.inertia_”实现。
import numpy as np
from sklearn.cluster import KMeans
import pylab as pltplt.rcParams['font.sans-serif'] = ['SimHei'] # 显示中文
a = np.loadtxt('data/data11_2.txt') # 加载数
b=(a-a.min(axis=0))/(a.max(axis=0)-a.min(axis=0)) # 标准化# 求出k对应的簇内离差平均和的和
SSE = []; K = range(2, len(a)+1)
for i in K:md = KMeans(i).fit(b)SSE.append(md.inertia_) # 它表示聚类结果的簇内平方误差和(Inertia)# 可视化
plt.figure(1)
plt.title('k值与离差平方和的关系曲线')
plt.plot(K, SSE,'*-');
# 生成想要的 x 轴刻度细化值
x_ticks = np.arange(2, 10, 1)
# 设置 x 轴刻度
plt.xticks(x_ticks)
plt.show()
通过上图可以看出k=3时,是个拐点。所有选择k=3。
轮廓系数法(十分客观)
定义样本点i的轮廓系数,S_i代表样本点i的轮廓系数,a_i代表该点到簇内其他点的距离的均值;b_i分两步,首先计算该点到其他簇内点距离的平均距离,然后将最小值作为b_i。a_i表示了簇内的紧密度,b_i表示了簇间的分散度。
k个簇的总轮廓点系数定义为所有样本点轮廓系数的平均值。因此计算量大
总轮廓系数越接近1,聚类效果越好。簇内平均距离小,簇间平均距离大。
调用sklearn.metrics中的silhouette_score(轮廓分数)函数实现
#程序文件ex11_7.py
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
plt.rcParams['font.sans-serif'] = ['SimHei']# 忽略警告
import warnings
# 使用过滤器来忽略特定类型的警告
warnings.filterwarnings("ignore")a = np.loadtxt('data/data11_2.txt')
b=(a-a.min(axis=0))/(a.max(axis=0)-a.min(axis=0))
S = []; K = range(2, len(a))
for i in K:md = KMeans(i).fit(b)labels = md.labels_S.append(silhouette_score(b, labels))
plt.figure(dpi = 300)
plt.title('k值与轮廓系数的关系曲线')
plt.plot(K, S,'*-'); plt.show()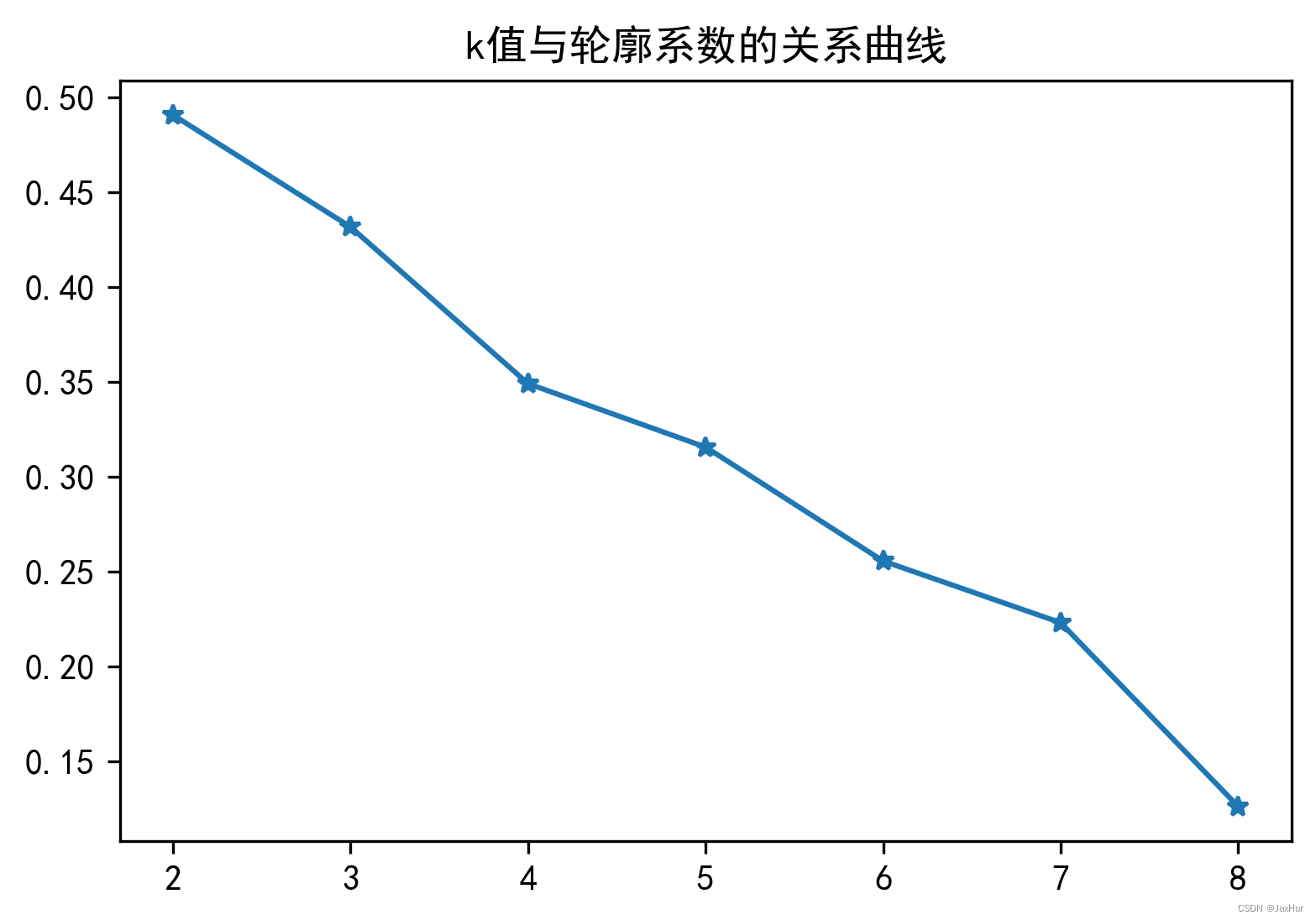
综上两种方法,好像并没有什么最好的方法,离差平均和不好判断,轮廓系数又像上面的情况。感觉综合两种方法比较好
相关文章:

【聚类】K-Means聚类
cluster:簇 原理: 这边暂时没有时间具体介绍kmeans聚类的原理。简单来说,就是首先初始化k个簇心;然后计算所有点到簇心的欧式距离,对一个点来说,距离最短就属于那个簇;然后更新不同簇的簇心&a…...
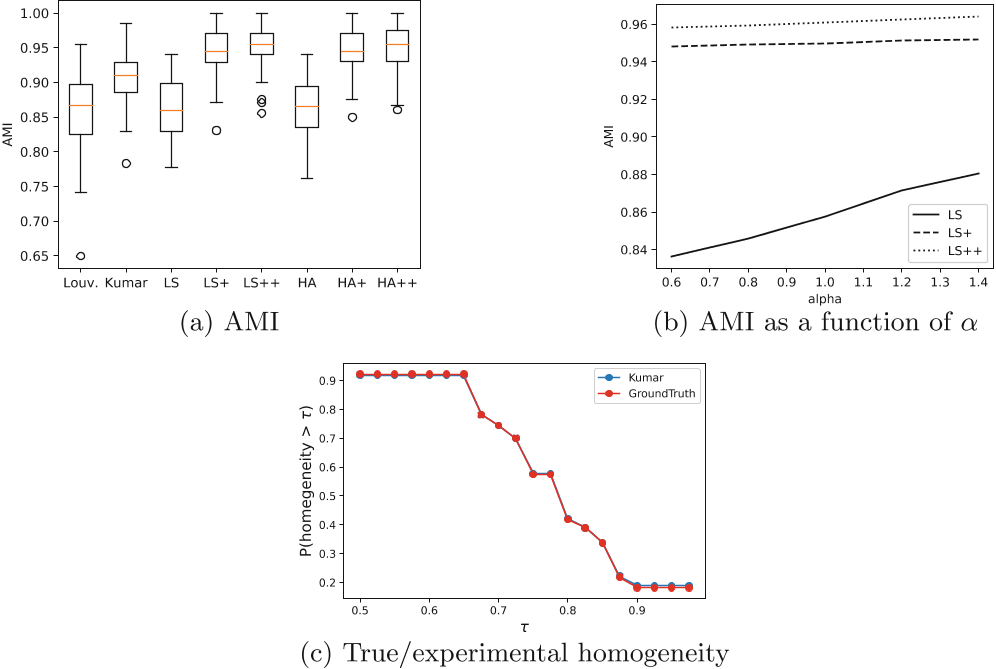
超图聚类论文阅读2:Last-step算法
超图聚类论文阅读2:Last-step算法 《使用超图模块化的社区检测算法》 《Community Detection Algorithm Using Hypergraph Modularity》 COMPLEX NETWORKS 2021, SCI 3区 具体实现源码见HyperNetX库 工作:提出了一种用于超图的社区检测算法。该算法的主要…...

React 防抖与节流用法
在React中,防抖和节流是优化性能和提升用户体验的常用技术。下面是它们的用法: 防抖(Debounce):防抖是指在某个事件触发后,等待一段时间后执行回调函数。如果在等待时间内再次触发该事件,将重新…...

发布 VectorTraits v1.0,它是 C# 下增强SIMD向量运算的类库
发布 VectorTraits v1.0, 它是C#下增强SIMD向量运算的类库 VectorTraits: SIMD Vector type traits methods (SIMD向量类型的特征方法). NuGet: https://www.nuget.org/packages/VectorTraits/1.0.0 源代码: https://github.com/zyl910/VectorTraits 用途 总所周知&#x…...

HCIA自学笔记01-冲突域
共享式网络(用同一根同轴电缆通信)中可能会出现信号冲突现象。 如图是一个10BASE5以太网,每个主机都是用同一根同轴电缆来与其它主机进行通信,因此,这里的同轴电缆又被称为共享介质,相应的网络被称为共享介…...

3D封装技术发展
长期以来,芯片制程微缩技术一直驱动着摩尔定律的延续。从1987年的1um制程到2015年的14nm制程,芯片制程迭代速度一直遵循摩尔定律的规律,即芯片上可以容纳的晶体管数目在大约每经过18个月到24个月便会增加一倍。但2015年以后,芯片制…...

探讨下live555用的编程设计模式
这个应该放到这里 7.live555mediaserver-第1阶段小结(完整对象图和思维导图) https://blog.csdn.net/yhb1206/article/details/127330771 但是想想,还是拿出来吧。 从这第1阶段就能发现,它实质用到了reactor网络编程模式。...
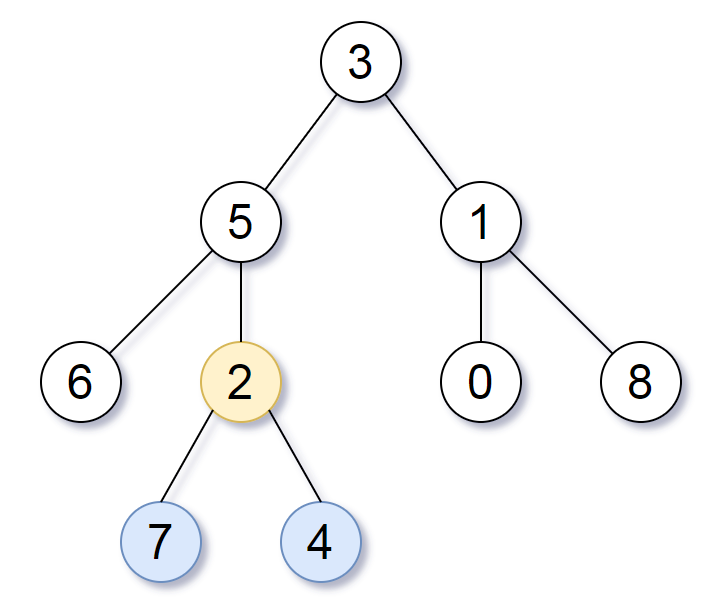
LeetCode 1123. Lowest Common Ancestor of Deepest Leaves【树,DFS,BFS,哈希表】1607
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
centroen 23版本换界面了
旧版本 新版本 没有与操作系统一起打包的ISO文件了,要么先安装系统,再安装Centreon,要么用pve导入OVF文件...
)
Postman 调用 Microsoft Graph API (InsCode AI 创作助手)
官方配置参考网址: https://learn.microsoft.com/zh-cn/graph/use-postman 获取 Azure AD 应用程序凭据: 在 Azure AD 中注册你的应用程序,并获取客户端ID和客户端密钥。这些凭据将允许你的应用程序与 Microsoft Graph 进行身份验证和访问权限…...

MySql 游标 触发器
游标 1.什么是游标 MySQL游标是一种数据库对象,它用于在数据库查询过程中迭代访问结果集中的每一行。游标可以被看作是一个指向查询结果集的指针,通过移动游标,可以按行读取和处理结果集的数据。在MySQL中,游标可以用于在存储过程…...
浅谈数据治理中的智能数据目录
在数字化转型的战略实施中,很多企业都在搭建自己的业务、数据及人工智能的中台。在同这些企业合作和交流中,越来越体会到数据目录是中台建设的核心和基础。为了更好地提供数据服务,发挥数据价值,用户需要先理解数据和信任数据。 企…...
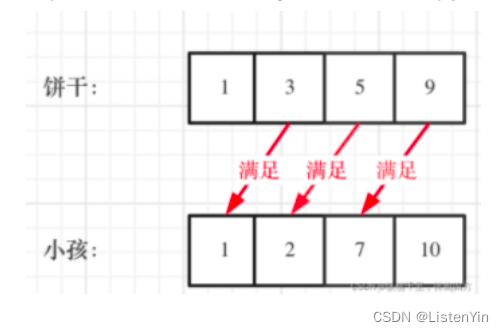
算法通关村第十七关:青铜挑战-贪心其实很简单
青铜挑战-贪心其实很简单 1. 难以解释的贪心算法 贪心学习法则:直接做题,不考虑贪不贪心 贪心(贪婪)算法 是指在问题尽心求解时,在每一步选择中都采取最好或者最优(最有利)的选择,从而希望能够导致结果最…...
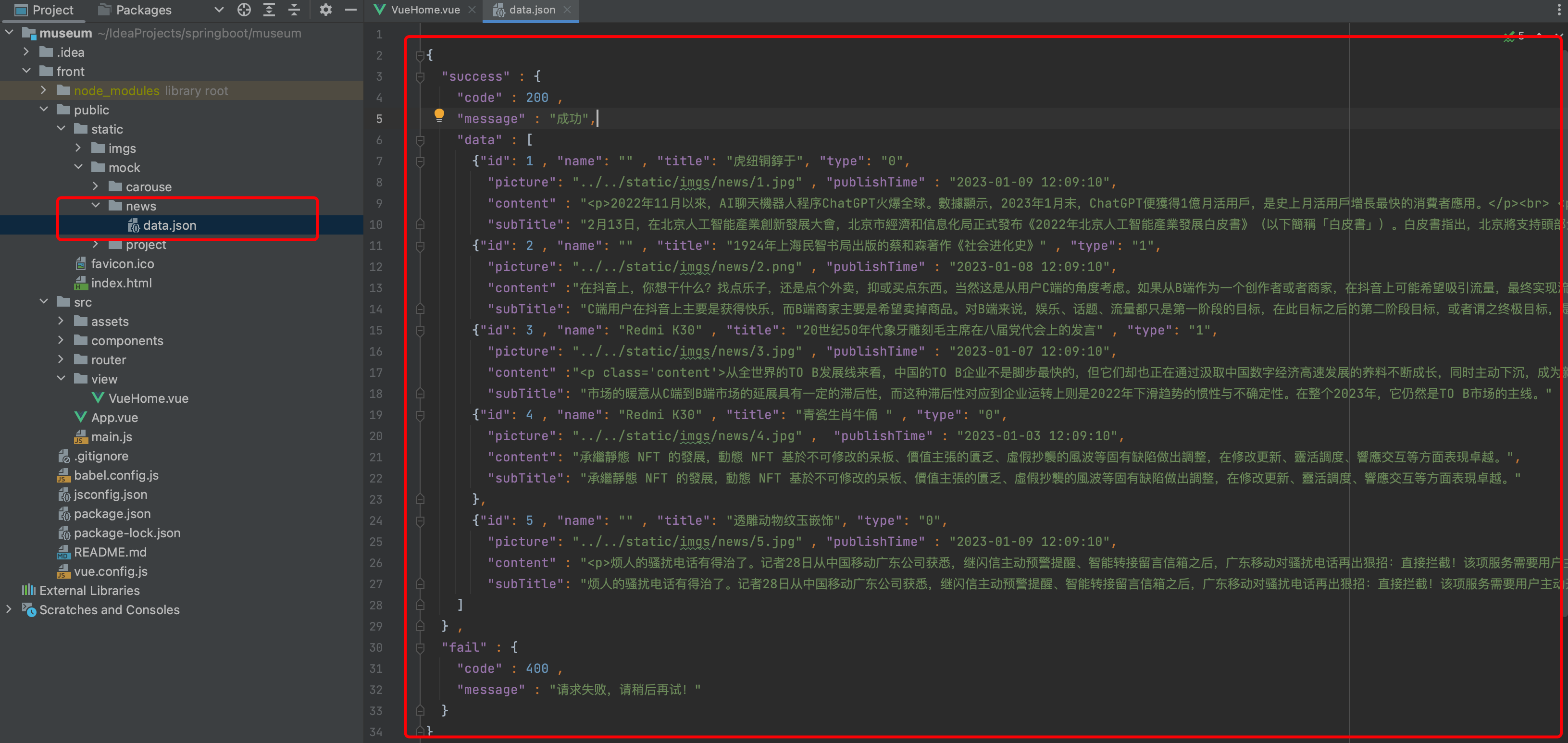
[Vue3 博物馆管理系统] 使用Vue3、Element-plus的Layout 布局构建组图文章
系列文章目录 第一章 定制上中下(顶部菜单、底部区域、中间主区域显示)三层结构首页 第二章 使用Vue3、Element-plus菜单组件构建菜单 第三章 使用Vue3、Element-plus走马灯组件构建轮播图 第四章 使用Vue3、Element-plus tabs组件构建选项卡功能 第五章…...

【LeetCode算法系列题解】第36~40题
CONTENTS LeetCode 36. 有效的数独(中等)LeetCode 37. 解数独(困难)LeetCode 38. 外观数列(中等)LeetCode 39. 组合总和(中等)LeetCode 40. 组合总和 II(中等)…...
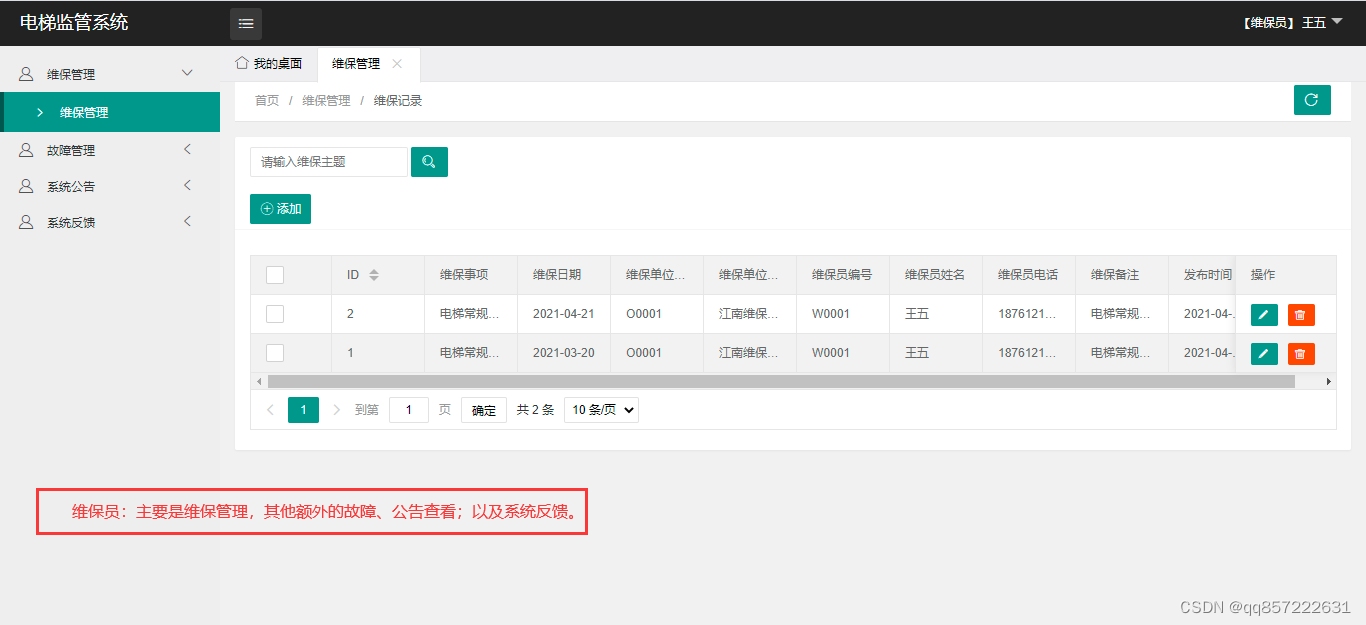
java+ssm+mysql电梯管理系统
项目介绍: 使用javassmmysql开发的电梯管理系统,系统包含管理员,监管员、安全员、维保员角色,功能如下: 管理员:系统用户管理(监管员、安全员、维保员);系统公告&#…...

最近读书了吗?林曦老师与你分享来自暄桐课堂的读书方法
近来,大家有在开心读书吗?对于读书,有一个很生动的说法:“无事常读书,一日是四日。若活七十年,便二百八十。”读书帮助我们超越个体生命经验的限制,此时此地的我们,也可借由书本&…...
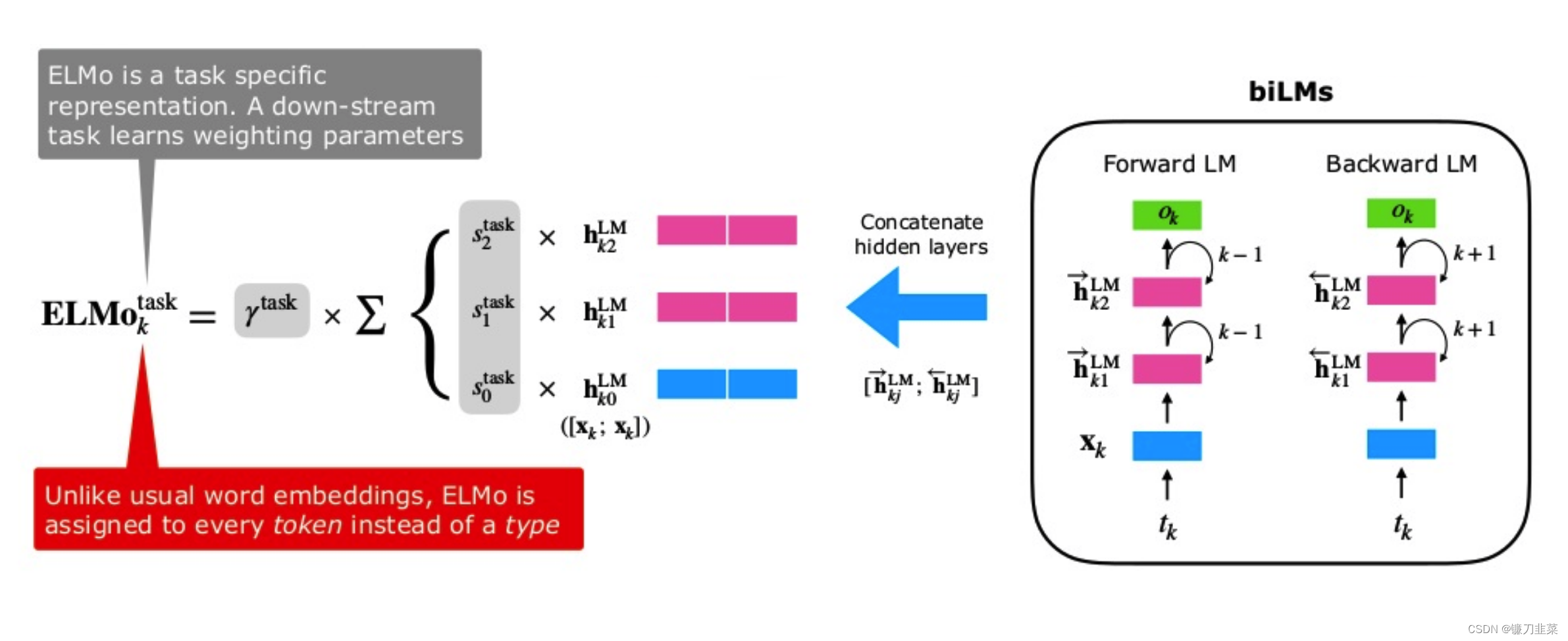
【AI理论学习】语言模型:从Word Embedding到ELMo
语言模型:从Word Embedding到ELMo ELMo原理Bi-LM总结参考资料 本文主要介绍一种建立在LSTM基础上的ELMo预训练模型。2013年的Word2Vec及2014年的GloVe的工作中,每个词对应一个vector,对于多义词无能为力。ELMo的工作对于此,提出了…...

多功能透明屏,在智能家居领域中,有哪些功能特点?显示、连接
多功能透明屏是一种新型的显示技术,它能够在透明的表面上显示图像和视频,并且具有多种功能。 这种屏幕可以应用于各种领域,如商业广告、智能家居、教育等,为用户提供更加便捷和多样化的体验。 首先,多功能透明屏可以…...
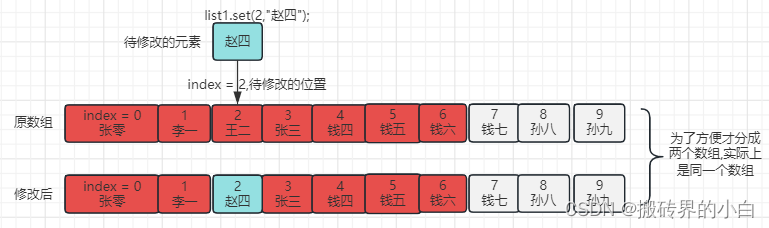
【List篇】ArrayList 详解(含图示说明)
Java中的ArrayList是一个动态数组,可以自动扩展容量以适应数据的添加和删除。它可以用来存储各种类型的数据,例如String,Integer,Boolean等。ArrayList实现了List接口,可以进行常见的List操作,例如添加、插…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...
