LeetCode 1123. Lowest Common Ancestor of Deepest Leaves【树,DFS,BFS,哈希表】1607
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章中,我不仅会讲解多种解题思路及其优化,还会用多种编程语言实现题解,涉及到通用解法时更将归纳总结出相应的算法模板。
为了方便在PC上运行调试、分享代码文件,我还建立了相关的仓库:https://github.com/memcpy0/LeetCode-Conquest。在这一仓库中,你不仅可以看到LeetCode原题链接、题解代码、题解文章链接、同类题目归纳、通用解法总结等,还可以看到原题出现频率和相关企业等重要信息。如果有其他优选题解,还可以一同分享给他人。
由于本系列文章的内容随时可能发生更新变动,欢迎关注和收藏征服LeetCode系列文章目录一文以作备忘。
给你一个有根节点 root 的二叉树,返回它 最深的叶节点的最近公共祖先 。
回想一下:
- 叶节点 是二叉树中没有子节点的节点
- 树的根节点的 深度 为
0,如果某一节点的深度为d,那它的子节点的深度就是d+1 - 如果我们假定
A是一组节点S的 最近公共祖先,S中的每个节点都在以A为根节点的子树中,且A的深度达到此条件下可能的最大值。
示例 1:
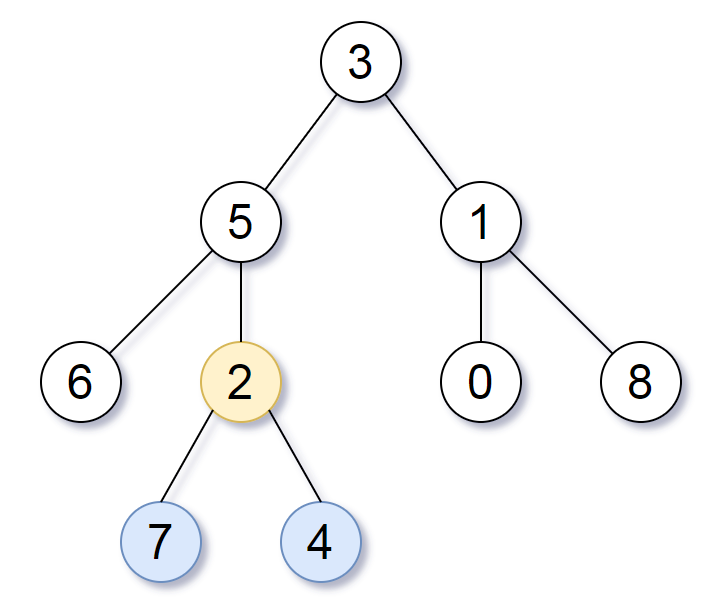
输入:root = [3,5,1,6,2,0,8,null,null,7,4]
输出:[2,7,4]
解释:我们返回值为 2 的节点,在图中用黄色标记。
在图中用蓝色标记的是树的最深的节点。
注意,节点 6、0 和 8 也是叶节点,但是它们的深度是 2 ,而节点 7 和 4 的深度是 3 。
示例 2:
输入:root = [1]
输出:[1]
解释:根节点是树中最深的节点,它是它本身的最近公共祖先。
示例 3:
输入:root = [0,1,3,null,2]
输出:[2]
解释:树中最深的叶节点是 2 ,最近公共祖先是它自己。
提示:
- 树中的节点数将在
[1, 1000]的范围内。 0 <= Node.val <= 1000- 每个节点的值都是 独一无二 的。
注意: 本题与力扣 865 重复:https://leetcode-cn.com/problems/smallest-subtree-with-all-the-deepest-nodes/
解法1 递归

看上图(示例 1),这棵树的节点 3 , 5 , 2 3,5,2 3,5,2 都是最深叶节点 7 , 4 7,4 7,4 的公共祖先,但只有节点 2 2 2 是最近的公共祖先。
如果我们要找的节点只在左子树中,那么最近公共祖先也必然只在左子树中。对于本题,如果左子树的最大深度比右子树的大,那么最深叶结点就只在左子树中,所以最近公共祖先也只在左子树中。反过来说,如果右子树的最大深度大于左子树,那么最深叶结点就只在右子树中,所以最近公共祖先也只在右子树中。
如果左右子树的最大深度一样呢?当前节点一定是最近公共祖先吗?不一定。比如节点 1 1 1 的左右子树最深叶节点 0 , 8 0,8 0,8 的深度都是 2 2 2 ,但该深度并不是全局最大深度,所以节点 1 1 1 并不能是答案。
根据以上讨论,正确做法如下:
- 递归这棵二叉树,同时维护全局最大深度 maxDepth \textit{maxDepth} maxDepth 。
- 在「递」的时候往下传 d e p t h depth depth ,用来表示当前节点的深度。
- 在「归」的时候往上传当前子树最深叶节点的深度。
- 设左子树最深叶节点的深度为 leftMaxDepth \textit{leftMaxDepth} leftMaxDepth ,右子树最深叶节点的深度为 rightMaxDepth \textit{rightMaxDepth} rightMaxDepth 。如果 leftMaxDepth = rightMaxDepth = maxDepth \textit{leftMaxDepth}=\textit{rightMaxDepth}=\textit{maxDepth} leftMaxDepth=rightMaxDepth=maxDepth ,那么更新答案为当前节点。注意这并不代表我们找到了答案,如果后面发现了更深的叶节点,那么答案还会更新。
class Solution {
public:TreeNode *lcaDeepestLeaves(TreeNode *root) {TreeNode *ans = nullptr;int max_depth = -1; // 全局最大深度function<int(TreeNode*, int)> dfs = [&](TreeNode *node, int depth) {if (node == nullptr) {max_depth = max(max_depth, depth); // 维护全局最大深度return depth;}int left_max_depth = dfs(node->left, depth + 1); // 获取左子树最深叶节点的深度int right_max_depth = dfs(node->right, depth + 1); // 获取右子树最深叶节点的深度if (left_max_depth == right_max_depth && left_max_depth == max_depth)ans = node;return max(left_max_depth, right_max_depth); // 当前子树最深叶节点的深度};dfs(root, 0);return ans;}
};
复杂度分析:
- 时间复杂度: O ( n ) \mathcal{O}(n) O(n) 。每个节点都会恰好访问一次。
- 空间复杂度: O ( n ) \mathcal{O}(n) O(n) 。最坏情况下,二叉树是一条链,递归需要 O(n)\mathcal{O}(n)O(n) 的栈空间。
解法2 自底向上
也可以不用全局变量,而是把每棵子树都看成是一个「子问题」,即对于每棵子树,我们需要知道:
- 这棵子树最深叶结点的深度。这里是指叶子在这棵子树内的深度,而不是在整棵二叉树的视角下的深度。相当于这棵子树的高度。
- 这棵子树的最深叶结点的最近公共祖先 lca \textit{lca} lca 。
分类讨论:
- 设子树的根节点为 n o d e node node, n o d e node node 的左子树的高度为 leftHeight \textit{leftHeight} leftHeight , n o d e node node 的右子树的高度为 rightHeight \textit{rightHeight} rightHeight 。
- 如果 l e f t H e i g h t > r i g h t H e i g h t leftHeight>rightHeight leftHeight>rightHeight ,那么子树的高度为 leftHeight + 1 \textit{leftHeight} + 1 leftHeight+1 , lca \textit{lca} lca 是左子树的 lca \textit{lca} lca 。
- 如果 leftHeight < rightHeight \textit{leftHeight} < \textit{rightHeight} leftHeight<rightHeight ,那么子树的高度为 r i g h t H e i g h t + 1 rightHeight+1 rightHeight+1 , l c a lca lca 是右子树的 l c a lca lca 。
- 如果 leftHeight = rightHeight \textit{leftHeight} = \textit{rightHeight} leftHeight=rightHeight ,那么子树的高度为 leftHeight + 1 \textit{leftHeight} + 1 leftHeight+1 , l c a lca lca 就是 n o d e node node 。反证法:如果 l c a lca lca 在左子树中,那么 l c a lca lca 不是右子树的最深叶结点的祖先,这不对;如果 l c a lca lca 在右子树中,那么 l c a lca lca 不是左子树的最深叶结点的祖先,这也不对;如果 l c a lca lca 在 n o d e node node 的上面,那就不符合「最近」的要求。所以 l c a lca lca 只能是 n o d e node node。
class Solution {pair<int, TreeNode*> dfs(TreeNode *node) {if (node == nullptr)return {0, nullptr};auto [left_height, left_lca] = dfs(node->left);auto [right_height, right_lca] = dfs(node->right);if (left_height > right_height) // 左子树更高return {left_height + 1, left_lca};if (left_height < right_height) // 右子树更高return {right_height + 1, right_lca};return {left_height + 1, node}; // 一样高}public:TreeNode *lcaDeepestLeaves(TreeNode *root) {return dfs(root).second;}
};
复杂度分析:
- 时间复杂度: O ( n ) \mathcal{O}(n) O(n) 。每个节点都会恰好访问一次。
- 空间复杂度: O ( n ) \mathcal{O}(n) O(n) 。最坏情况下,二叉树是一条链,递归需要 O ( n ) \mathcal{O}(n) O(n) 的栈空间。
更简洁的写法是:
class Solution {
public:int depth[1010];TreeNode* lcaDeepestLeaves(TreeNode* root) {if (root == nullptr) return nullptr;TreeNode* left = root->left, *right = root->right;TreeNode* lcaLeft = lcaDeepestLeaves(root->left), *lcaRight = lcaDeepestLeaves(root->right);int dl = left ? depth[left->val] : 0, dr = right ? depth[right->val] : 0;depth[root->val] = max(dl, dr) + 1;if (dl > dr) return lcaLeft;if (dr > dl) return lcaRight;return root;}
};
相关文章:

LeetCode 1123. Lowest Common Ancestor of Deepest Leaves【树,DFS,BFS,哈希表】1607
本文属于「征服LeetCode」系列文章之一,这一系列正式开始于2021/08/12。由于LeetCode上部分题目有锁,本系列将至少持续到刷完所有无锁题之日为止;由于LeetCode还在不断地创建新题,本系列的终止日期可能是永远。在这一系列刷题文章…...
centroen 23版本换界面了
旧版本 新版本 没有与操作系统一起打包的ISO文件了,要么先安装系统,再安装Centreon,要么用pve导入OVF文件...
)
Postman 调用 Microsoft Graph API (InsCode AI 创作助手)
官方配置参考网址: https://learn.microsoft.com/zh-cn/graph/use-postman 获取 Azure AD 应用程序凭据: 在 Azure AD 中注册你的应用程序,并获取客户端ID和客户端密钥。这些凭据将允许你的应用程序与 Microsoft Graph 进行身份验证和访问权限…...

MySql 游标 触发器
游标 1.什么是游标 MySQL游标是一种数据库对象,它用于在数据库查询过程中迭代访问结果集中的每一行。游标可以被看作是一个指向查询结果集的指针,通过移动游标,可以按行读取和处理结果集的数据。在MySQL中,游标可以用于在存储过程…...
浅谈数据治理中的智能数据目录
在数字化转型的战略实施中,很多企业都在搭建自己的业务、数据及人工智能的中台。在同这些企业合作和交流中,越来越体会到数据目录是中台建设的核心和基础。为了更好地提供数据服务,发挥数据价值,用户需要先理解数据和信任数据。 企…...
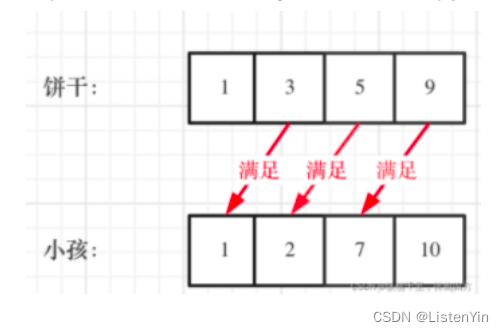
算法通关村第十七关:青铜挑战-贪心其实很简单
青铜挑战-贪心其实很简单 1. 难以解释的贪心算法 贪心学习法则:直接做题,不考虑贪不贪心 贪心(贪婪)算法 是指在问题尽心求解时,在每一步选择中都采取最好或者最优(最有利)的选择,从而希望能够导致结果最…...
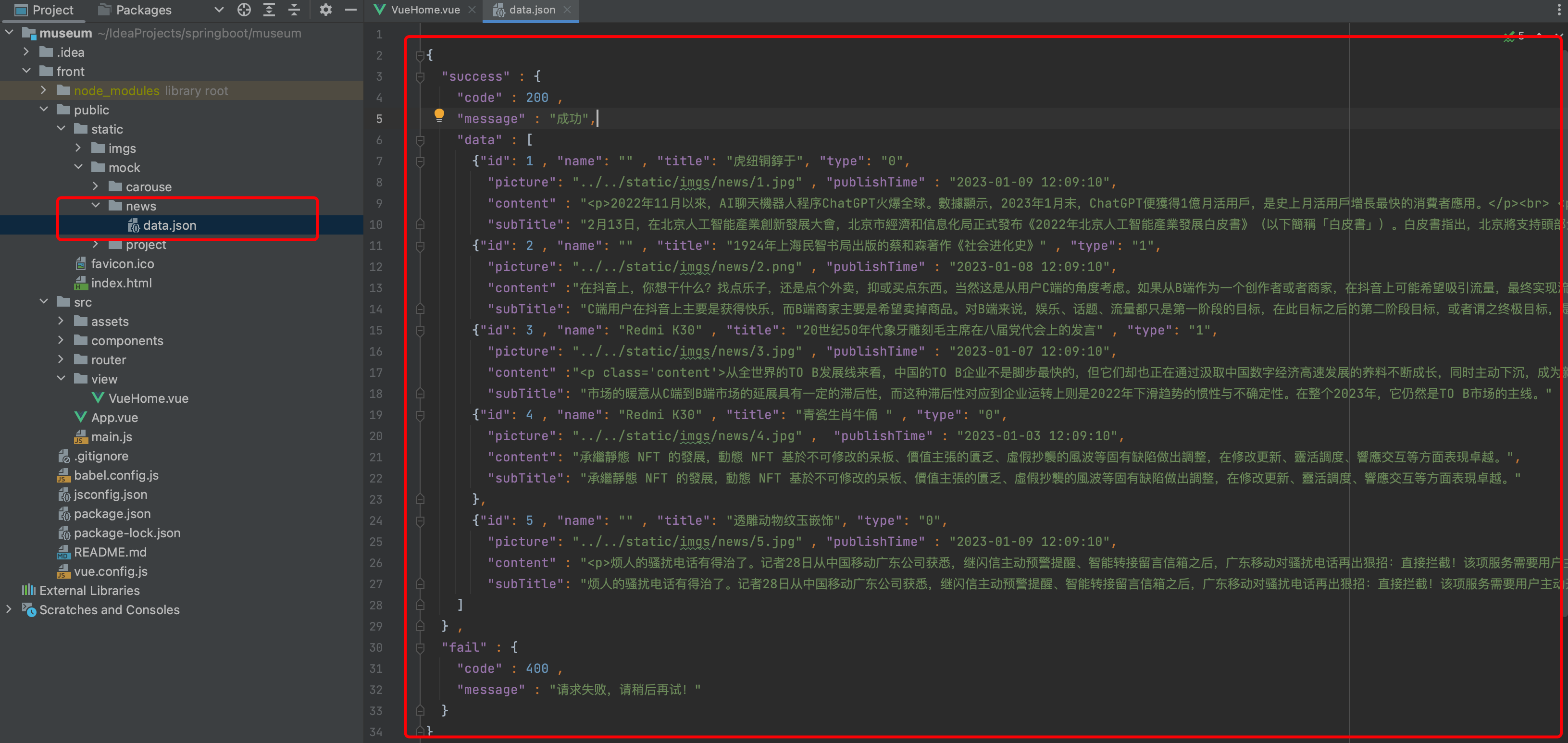
[Vue3 博物馆管理系统] 使用Vue3、Element-plus的Layout 布局构建组图文章
系列文章目录 第一章 定制上中下(顶部菜单、底部区域、中间主区域显示)三层结构首页 第二章 使用Vue3、Element-plus菜单组件构建菜单 第三章 使用Vue3、Element-plus走马灯组件构建轮播图 第四章 使用Vue3、Element-plus tabs组件构建选项卡功能 第五章…...

【LeetCode算法系列题解】第36~40题
CONTENTS LeetCode 36. 有效的数独(中等)LeetCode 37. 解数独(困难)LeetCode 38. 外观数列(中等)LeetCode 39. 组合总和(中等)LeetCode 40. 组合总和 II(中等)…...
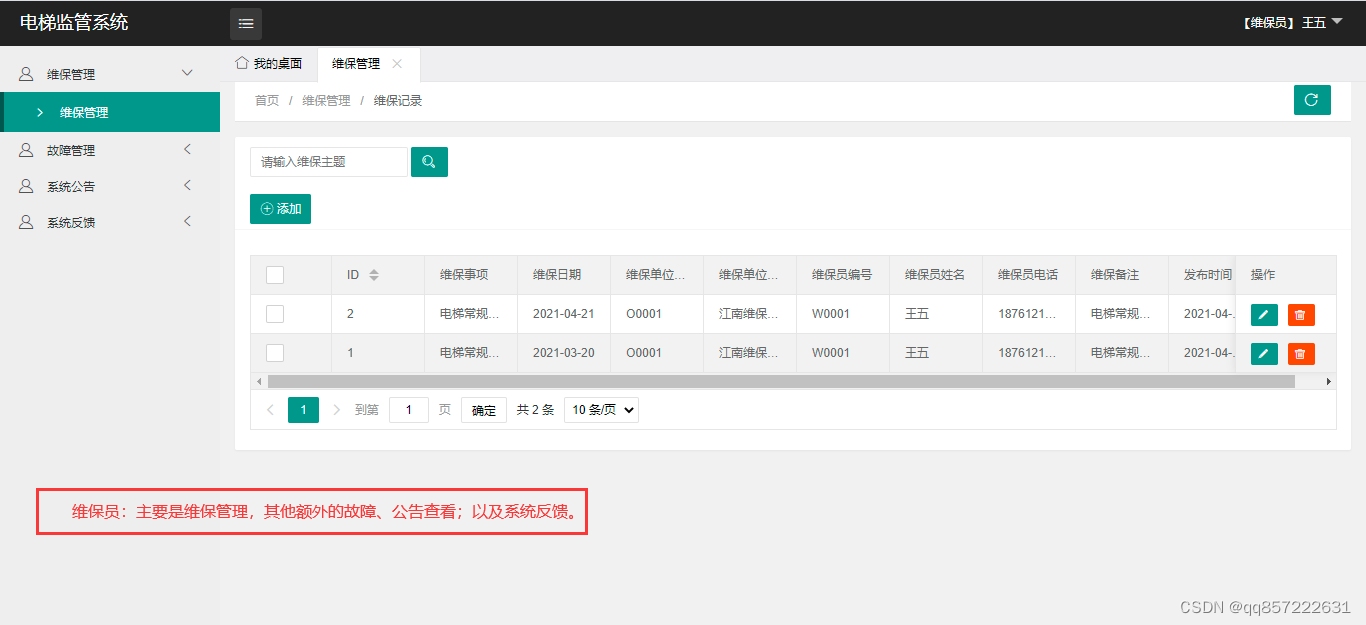
java+ssm+mysql电梯管理系统
项目介绍: 使用javassmmysql开发的电梯管理系统,系统包含管理员,监管员、安全员、维保员角色,功能如下: 管理员:系统用户管理(监管员、安全员、维保员);系统公告&#…...

最近读书了吗?林曦老师与你分享来自暄桐课堂的读书方法
近来,大家有在开心读书吗?对于读书,有一个很生动的说法:“无事常读书,一日是四日。若活七十年,便二百八十。”读书帮助我们超越个体生命经验的限制,此时此地的我们,也可借由书本&…...
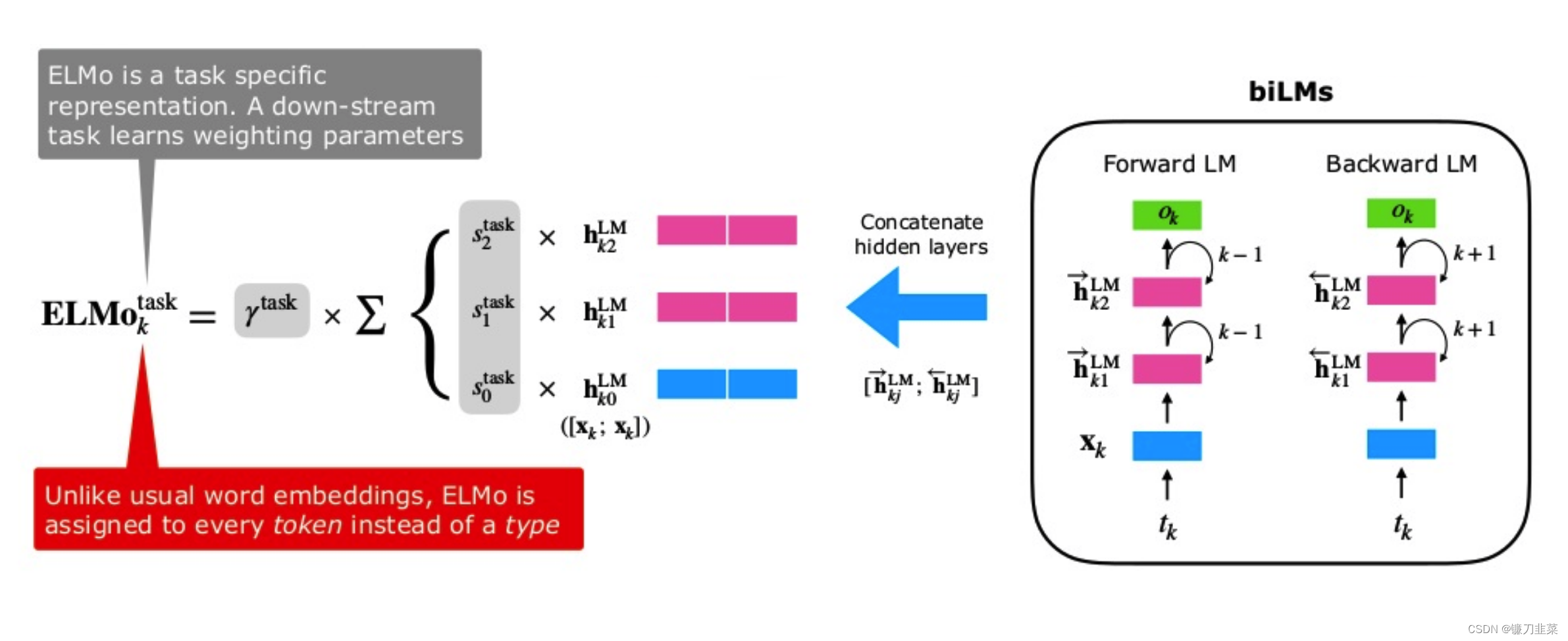
【AI理论学习】语言模型:从Word Embedding到ELMo
语言模型:从Word Embedding到ELMo ELMo原理Bi-LM总结参考资料 本文主要介绍一种建立在LSTM基础上的ELMo预训练模型。2013年的Word2Vec及2014年的GloVe的工作中,每个词对应一个vector,对于多义词无能为力。ELMo的工作对于此,提出了…...

多功能透明屏,在智能家居领域中,有哪些功能特点?显示、连接
多功能透明屏是一种新型的显示技术,它能够在透明的表面上显示图像和视频,并且具有多种功能。 这种屏幕可以应用于各种领域,如商业广告、智能家居、教育等,为用户提供更加便捷和多样化的体验。 首先,多功能透明屏可以…...
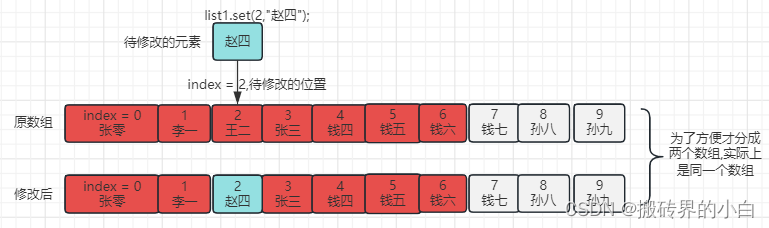
【List篇】ArrayList 详解(含图示说明)
Java中的ArrayList是一个动态数组,可以自动扩展容量以适应数据的添加和删除。它可以用来存储各种类型的数据,例如String,Integer,Boolean等。ArrayList实现了List接口,可以进行常见的List操作,例如添加、插…...

SSL证书只有收费的吗?有没有免费使用的?
首先明白SSL证书是什么SSL英文全称:英文全称: Secure Socket Layer Certificate,中文全称:安全套接字层证书。 SSL是一种由数字证书颁发机构(CA) 签发的数字证书。它用于建立安全的加密连接,确保通过网络传输的数据在客户端和服务器之间的安全性和完整性…...

48V轻混技术
文章目录 48V轻混技术的主要特点和优势48V轻混技术的优缺点优点:缺点: 48V轻混技术的主要特点和优势 48V轻混技术(48V Mild Hybrid Technology)是一种汽车动力系统技术,它结合了内燃机和电动机的优势,以提…...

机器学习基础算法--回归类型和评价分析
目录 1.数据归一化处理 2.数据标准化处理 3.Lasso回归模型 4.岭回归模型 5.评价指标计算 1.数据归一化处理 """ x的归一化的方法还是比较多的我们就选取最为基本的归一化方法 x(x-x_min)/(x_max-x_min) """ import numpy as np from sklea…...

MATLAB 软件功能简介
MATLAB 的名称源自 Matrix Laboratory,1984 年由美国 Mathworks 公司推向市场。 它是一种科学计算软件,专门以矩阵的形式处理数据。MATLAB 将高性能的数值计算和可 视化集成在一起,并提供了大量的内置函数,从而被广泛的应用于科学计算、控制…...
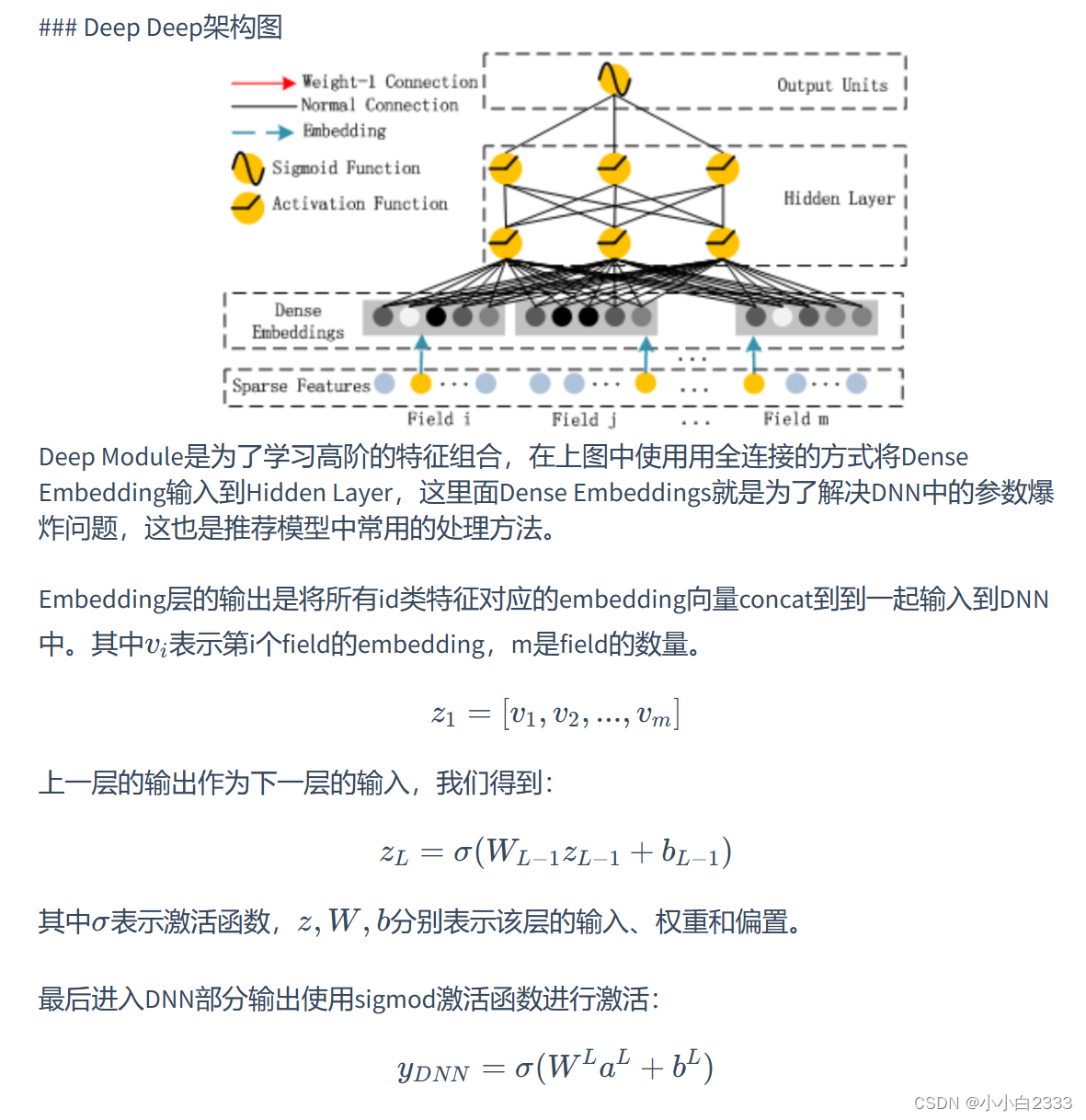
deepfm内容理解
对于CTR问题,被证明的最有效的提升任务表现的策略是特征组合(Feature Interaction); 两个问题: 如何更好地学习特征组合,进而更加精确地描述数据的特点; 如何更高效的学习特征组合。 DNN局限 :当我们使…...
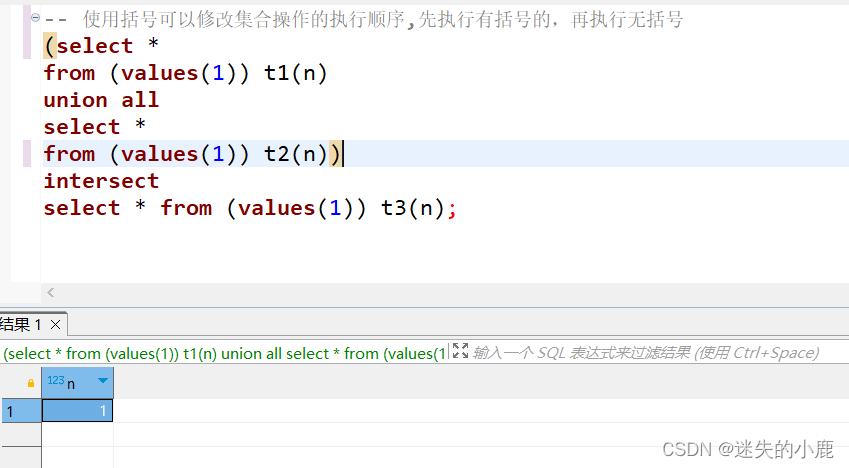
postgresql-集合运算
postgresql-集合运算 并集交集差集集合运算符的优先级 并集 create table excellent_emp( year int not null, emp_id integer not null, constraint pk_excellent_emp primary key(year,emp_id) );insert into excellent_emp values(2018,9); insert into excellent_emp value…...

[持续更新]计算机经典面试题基础篇Day2
[通用]计算机经典面试题基础篇Day2 1、单例模式是什么,线程安全吗 单例模式是一种设计模式,旨在确保一个类只有一个实例,并提供全局访问点。通过使用单例模式,可以避免多次创建相同的对象,节省内存资源,同…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...
