独享IP vs. 共享IP:哪种更适合你?
无论是个人用户还是企业组织,在互联网上都需要一个唯一标识来与其他设备进行通信。这就涉及到使用独立分配给自己或多个用户分享的公共 IP 地址(也称为共享 IP)。那么,究竟应该选择独占一个专用地址还是与他人分享相同地址呢?接下来我们将深入比较并找出答案。
独享IP
什么是独享IP?
所谓「独享」指得就像字面意义般只有单个实例可以拥有特定专属地址。
优点:高速、稳定且可靠。
缺点:成本高、资源浪费。
独享IP适用场景
如何判断是否需要独享IP?
在以下场景中,您可能更适合选择独享 IP:
- 需要高速稳定的网络连接:对于企业、金融机构等有较高网络需求的行业来说,拥有独占 IP 可以提供更快速和可靠的连接。
- 数据隐私与安全性要求较高:如果您处理敏感数据、进行在线交易或需要遵守特定法规标准时,使用专属 IP 地址可以增强数据保护。
对于倾向匿名浏览的个体,是否值得选择独享I P?
若你是一个注重个人隐私且希望能够匿名上网冲浪而不被追踪到自己真实身份,则共用公共地址比起具备唯一封包头部信息的专属地址会显得更加理想。通过与其他用户分享同一IP地址,在互联网上隐藏了你自己,并使跟踪变得困难。
共享I P
什么是共享I P?
所谓「共享」指代着多数客户都将获取并利用该单点上的IP位址。
优点 : 成本低、资源有效利用。
缺点 : 可能存在安全风险。
共享IP适用场景
对于以下场景中的个人用户或小型组织来说,选择共享 IP 是一个不错的选择: - 资金有限:如果您拥有较少资金,并且无法承担独占 IP 带来的高额费用,则可以选择使用共享 IP 来节约成本。
- 非敏感数据处理和一般网络活动:如果您只是进行普通浏览、社交媒体访问以及非关键业务操作等一般互联网活动,并且没有特别要求保护隐私和数据安全方面时,则可考虑使用共享 IP。
通过对独享 IP 和共分享比较,我们可以看到它们各自在不同场景下所具备的优劣。若追求更高速度、稳定性并愿意投入专属资源,在商务环境或需要强调隐私与安全性时推荐选取独享IP;而当预算相对紧张又做着日常网络行为(例如浏览器搜索)则建议采纳共享资源。
注意事项:
无论选择哪种类型的IP,请确保采取额外措施加强网络安全防护,并根据实际需求权衡其所带来的利与弊。
相关文章:

独享IP vs. 共享IP:哪种更适合你?
无论是个人用户还是企业组织,在互联网上都需要一个唯一标识来与其他设备进行通信。这就涉及到使用独立分配给自己或多个用户分享的公共 IP 地址(也称为共享 IP)。那么,究竟应该选择独占一个专用地址还是与他人分享相同地址呢&…...

【Arduino27】DHT11温湿度传感器模拟值实验
硬件准备 DHT11温湿度:1个 面包板:1个 杜邦线:3根 硬件连线 VDD引脚接 5V 电源 DATE引脚接 4号 接口 GND引脚接 GND 接口 软件程序 #include<DHT.h>#define DHT11_pin 4 //温湿度传感器引脚DHT dht(DHT11_pin,DHT11);float tem…...

dockerfile基于apline将JDK20打包成镜像
dockerfile基于apline将JDK20打包成镜像 今天就来和大家聊聊如何把最新出版的JDK20打包成docker镜像,很多uu都会采用centos作为基础镜像,这么做会有一个问题,centos系统会含有很多库文件,这些库文件JDK程序并不是完全需要的&a…...

MATLAB基础-MAT文件的读写操作
简介 MAT文件是MATLAB格式的双精度二进制数据文件,由MATLAB软件创建,可以使用MATLAB软件再其他计算机上以其他浮点格式读取,同时也可以使用其他软件通过MATLAB的应用程序接口来进行读写操作。如果只是再MATLAB环境中处理数据,使用…...

PostgreSQL PG15 新功能 PG_WALINSPECT
开头还是介绍一下群,如果感兴趣PolarDB ,MongoDB ,MySQL ,PostgreSQL ,Redis ,Oracle ,Oceanbase 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请加微信号 liuaustin3 (…...

时序预测 | MATLAB实现TCN-BiLSTM时间卷积双向长短期记忆神经网络时间序列预测
时序预测 | MATLAB实现TCN-BiLSTM时间卷积双向长短期记忆神经网络时间序列预测 目录 时序预测 | MATLAB实现TCN-BiLSTM时间卷积双向长短期记忆神经网络时间序列预测预测效果基本介绍模型描述程序设计参考资料 预测效果 基本介绍 1.MATLAB实现TCN-BiLSTM时间卷积双向长短期记忆神…...

数据结构和算法(2):向量
抽象数据类型 数组到向量 C/C 中,数组A[]中的元素与[0,n)内的编号一一对应,A[0],A[1],...,A[n-1];反之,每个元素均由(非负)编号唯一指代,并可直接访问A[i] 的物理地址 Ai s,s 为单…...

mysql 大表如何ddl
大家好,我是蓝胖子,mysql对大表(千万级数据)的ddl语句,在生产上执行时一定要千万小心,一不小心就有可能造成业务阻塞,数据库io和cpu飙高的情况。今天我们就来看看如何针对大表执行ddl语句。 通过这篇文章,…...
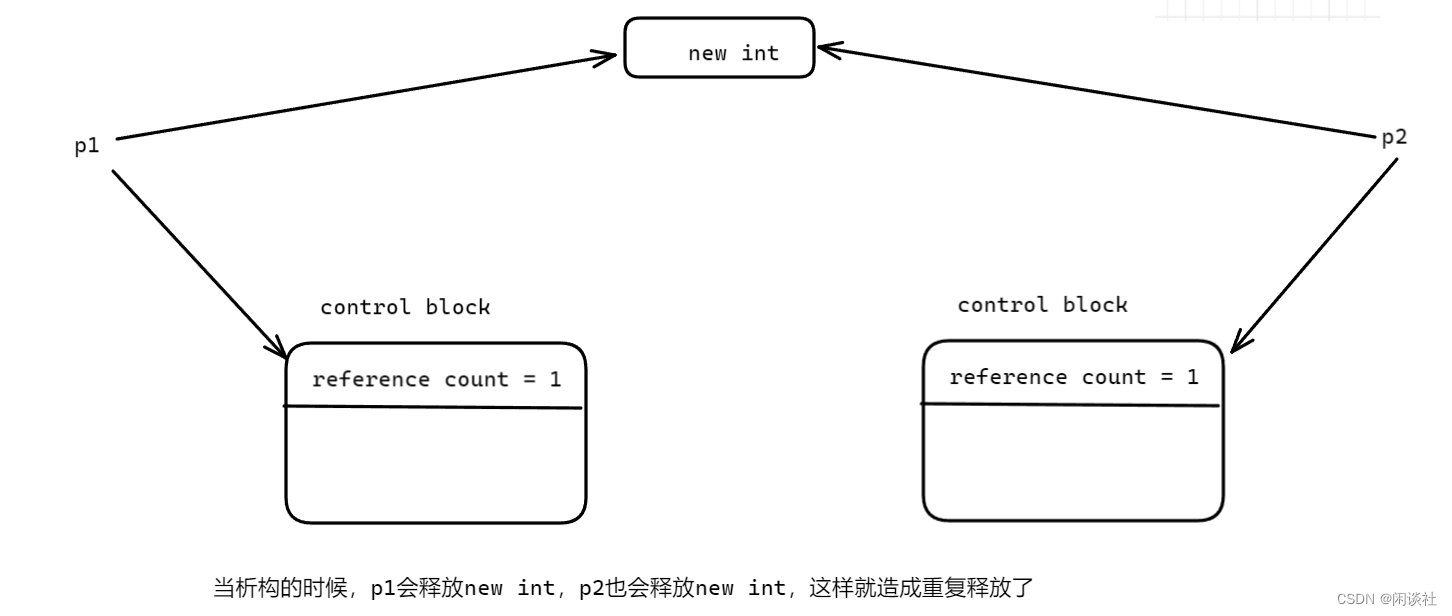
C++新特性:智能指针
一 、为什么需要智能指针 智能指针主要解决以下问题: 1)内存泄漏:内存手动释放,使用智能指针可以自动释放 2)共享所有权指针的传播和释放,比如多线程使用同一个对象时析构问题,例如同样的数据…...
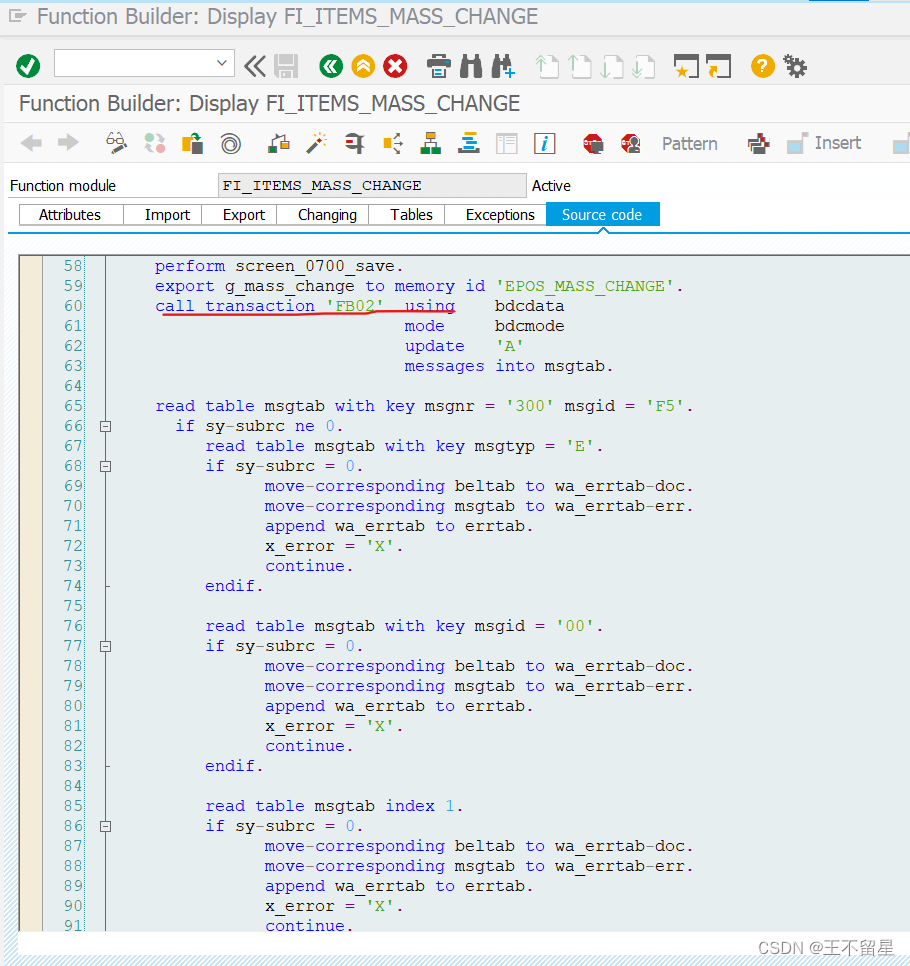
SAP FI之批量修改财务凭证的BAPI
文章目录 前言一、pandas是什么?二、使用步骤 1.引入库2.读入数据总结 前言 一般涉及修改财务凭证,或者其它凭证,不应直接更新数据库,而是使用系统提供的function module,或者BAPI,或者使用BDC。 一、 示例…...

Spring Boot + Vue的网上商城之商品分类
Spring Boot Vue的网上商城之商品分类 在网上商城中,商品分类是非常重要的一个功能,它可以帮助用户更方便地浏览和筛选商品。本文将介绍如何使用Spring Boot和Vue来实现商品分类的功能,包括一级分类和二级分类的管理以及前台按分类浏览商品…...

Docker 容器逃逸漏洞 (CVE-2020-15257)复现
漏洞概述 containerd是行业标准的容器运行时,可作为Linux和Windows的守护程序使用。在版本1.3.9和1.4.3之前的容器中,容器填充的API不正确地暴露给主机网络容器。填充程序的API套接字的访问控制验证了连接过程的有效UID为0,但没有以其他方式…...
Python 如何使用 csv、openpyxl 库进行读写 Excel 文件详细教程(更新中)
csv 基本概述 首先介绍下 csv (comma separated values),即逗号分隔值(也称字符分隔值,因为分隔符可以不是逗号),是一种常用的文本格式,用以存储表格数据,包括数字或者字符。 程序在处理数据时…...

$nextTick属性使用与介绍
属性介绍 $nextTick 是 Vue.js 中的一个重要方法,之前我们也说过$ref 等一些重要的属性,这次我们说$nextTick,$nextTick用于在 DOM 更新后执行回调函数。它通常用于处理 DOM 更新后的操作,因为 Vue 在更新 DOM 后不会立即触发回调…...

【群智能算法改进】一种改进的鹈鹕优化算法 IPOA算法[2]【Matlab代码#58】
文章目录 【获取资源请见文章第5节:资源获取】1. 原始POA算法2. 改进后的IPOA算法2.1 随机对立学习种群初始化2.2 动态权重系数2.3 透镜成像折射方向学习 3. 部分代码展示4. 仿真结果展示5. 资源获取 【获取资源请见文章第5节:资源获取】 1. 原始POA算法…...

k8s 入门到实战--部署应用到 k8s
k8s 入门到实战 01.png 本文提供视频版: 背景 最近这这段时间更新了一些 k8s 相关的博客和视频,也收到了一些反馈;大概分为这几类: 公司已经经历过服务化改造了,但还未接触过云原生。公司部分应用进行了云原生改造&…...

编程语言新特性:instanceof的改进
以前也写过类似的博文,可能重复。 要判断一个对象是哪个类或父类的实例,JAVA用到instanceof,其实语言也有类似语法。而类一般是多层继承的,有时就让人糊涂。所以我提出改进思路: instanceof:保持不变。ins…...
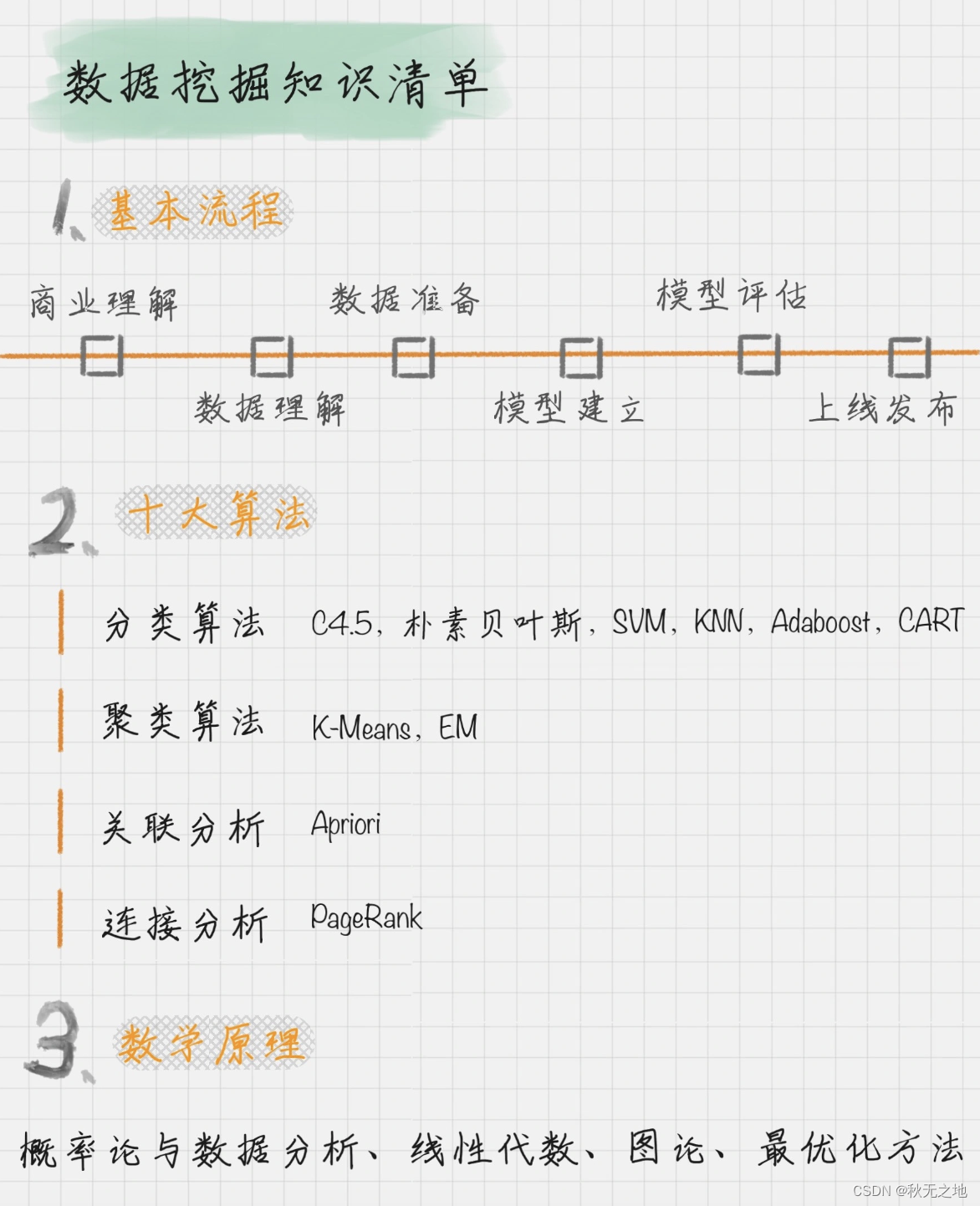
数据挖掘的学习路径
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据…...
逻辑回归Logistic
回归 概念 假设现在有一些数据点,我们用一条直线对这些点进行拟合(这条直线称为最佳拟合直线),这个拟合的过程就叫做回归。进而可以得到对这些点的拟合直线方程。 最后结果用sigmoid函数输出 因此,为了实现 Logisti…...
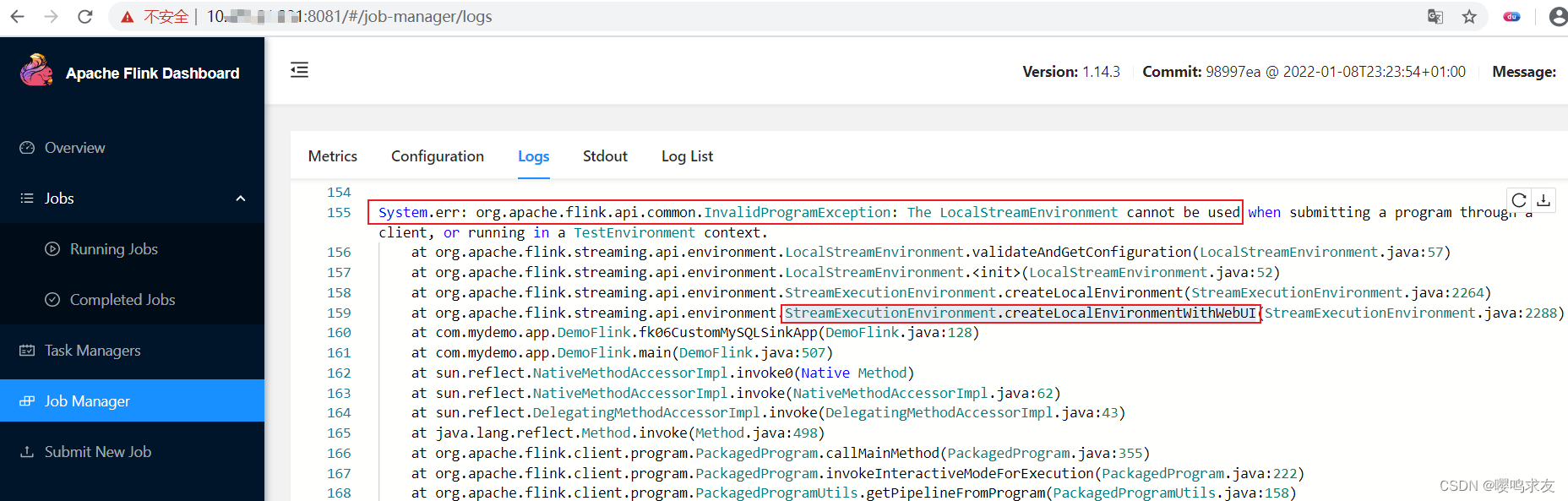
Flink提交jar出现错误RestHandlerException: No jobs included in application.
今天打包一个flink的maven工程为jar,通过flink webUI提交,发现居然报错。 如上图所示,提示错误为: Server Response Message: org.apache.flink.runtime.rest.handler.RestHandlerException: No jobs included in application. …...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...
