机器学习——boosting之GBDT
现在要开始重点关注名字了,名字透漏了很多信息!名字暗藏线索!
GBDT,Gradient Boosting Decision Tree: 梯度提升决策树
果然信息很丰富
梯度:意味着计算有迭代递进关系,但还不明确是怎么迭代递进的
提升:意味着前向分布式+加法模型,并且分类器之间是有相关提升的
决策树:CART决策树、C4.5、忘记名字了…
em…还是要再深挖深挖,小小的boosting,挖呀挖呀挖呀挖。。。
经过推导。。。发现,我的GBDT回归,实际就是上一篇提升树的二叉回归树…
看来可以省点儿功夫,不写代码,但可以稍微推导一下
首先,明确回归问题采用平方损失函数: L o s s ( y , f ( x ) ) = ( y − f ( x ) ) 2 Loss(y,f(x)) =(y-f(x))^2 Loss(y,f(x))=(y−f(x))2
其中,f(x) 是强分类器,且当前强分类器 f m = f m − 1 + T m ( x , θ m ) f_m = f_{m-1}+T_m(x,θ_m) fm=fm−1+Tm(x,θm)
问题来了,我们现在要求Loss最小,原本是可以直接使Loss对x求导,进而求出θ,得到强分类器的
但书上说了,有时候Loss对x求导,是无法实现的,说实话,我不知道为什么
不过,不妨碍我对GBDT进行推导
首先,梯度,是想要Loss成梯度逐步下降,那就采用让Loss在 f ( x ) = f m − 1 ( x ) f(x)=f_{m-1}(x) f(x)=fm−1(x)处进行一阶泰勒展开
则有 L o s s ( y , f ( x ) ) = L o s s ( y , f m − 1 ( x ) ) + ə L ( y , f m − 1 ( x ) ) ə f m − 1 ( x ) ∗ [ f ( x ) − f m − 1 ( x ) ] Loss(y,f(x)) = Loss(y,f_{m-1}(x))+\frac{ə_{L(y,f_{m-1}(x))}}{ə_{f_{m-1}(x)}}*[f(x)-f_{m-1}(x)] Loss(y,f(x))=Loss(y,fm−1(x))+əfm−1(x)əL(y,fm−1(x))∗[f(x)−fm−1(x)]
令 f ( x ) = f m ( x ) f(x) = f_m(x) f(x)=fm(x),则有
L ( y , f m ( x ) ) = L ( y , f m − 1 ( x ) ) + ə L ( y , f m − 1 ( x ) ) ə f m − 1 ( x ) ∗ [ f m ( x ) − f m − 1 ( x ) ] L(y,f_m(x)) = L(y,f_{m-1}(x))+\frac{ə_{L(y,f_{m-1}(x))}}{ə_{f_{m-1}(x)}}*[f_m(x)-f_{m-1}(x)] L(y,fm(x))=L(y,fm−1(x))+əfm−1(x)əL(y,fm−1(x))∗[fm(x)−fm−1(x)]
Δ L o s s = L ( y , f m ( x ) ) − L ( y , f m − 1 ( x ) ) = ə L ( y , f m − 1 ( x ) ) ə f m − 1 ( x ) ∗ [ f m ( x ) − f m − 1 ( x ) ] ΔLoss = L(y,f_m(x)) - L(y,f_{m-1}(x))=\frac{ə_{L(y,f_{m-1}(x))}}{ə_{f_{m-1}(x)}}*[f_m(x)-f_{m-1}(x)] ΔLoss=L(y,fm(x))−L(y,fm−1(x))=əfm−1(x)əL(y,fm−1(x))∗[fm(x)−fm−1(x)]
其中 [ f m ( x ) − f m − 1 ( x ) ] = T ( x , θ m ) [f_m(x)-f_{m-1}(x)] = T(x,θ_m) [fm(x)−fm−1(x)]=T(x,θm)
要使下一次迭代时,Loss降低,则需要ΔLoss<0,那么对应的 ə L ( y , f m − 1 ( x ) ) ə f m − 1 ( x ) ∗ T ( x , θ m ) \frac{ə_{L(y,f_{m-1}(x))}}{ə_{f_{m-1}(x)}}*T(x,θ_m) əfm−1(x)əL(y,fm−1(x))∗T(x,θm)<0
那么,当 T ( x , θ m ) = − ə L ( y , f m − 1 ( x ) ) ə f m − 1 ( x ) T(x,θ_m)=-\frac{ə_{L(y,f_{m-1}(x))}}{ə_{f_{m-1}(x)}} T(x,θm)=−əfm−1(x)əL(y,fm−1(x))时,就可以保证 ə L ( y , f m − 1 ( x ) ) ə f m − 1 ( x ) ∗ T ( x , θ m ) \frac{ə_{L(y,f_{m-1}(x))}}{ə_{f_{m-1}(x)}}*T(x,θ_m) əfm−1(x)əL(y,fm−1(x))∗T(x,θm)<0
因此, T ( x , θ m ) = − ə L ( y , f m − 1 ( x ) ) ə f m − 1 ( x ) = ə ( y − f m − 1 ( x ) ) 2 ə f m − 1 ( x ) T(x,θ_m)=-\frac{ə_{L(y,f_{m-1}(x))}}{ə_{f_{m-1}(x)}}=\frac{ə_{(y-f_{m-1}(x))^2}}{ə_{f_{m-1}(x)}} T(x,θm)=−əfm−1(x)əL(y,fm−1(x))=əfm−1(x)ə(y−fm−1(x))2
为了求解简洁美观,可以 令 L o s s 为 1 2 ( y − f ( x ) ) 2 令Loss为\frac{1}{2}(y-f(x))^2 令Loss为21(y−f(x))2
这样 T ( x , θ m ) = − ə L ( y , f m − 1 ( x ) ) ə f m − 1 ( x ) = 1 2 ə ( y − f m − 1 ( x ) ) 2 ə f m − 1 ( x ) = y − f m − 1 ( x ) T(x,θ_m)=-\frac{ə_{L(y,f_{m-1}(x))}}{ə_{f_{m-1}(x)}}=\frac{\frac{1}{2}ə_{(y-f_{m-1}(x))^2}}{ə_{f_{m-1}(x)}}=y-f_{m-1}(x) T(x,θm)=−əfm−1(x)əL(y,fm−1(x))=əfm−1(x)21ə(y−fm−1(x))2=y−fm−1(x)
哦!这不就是残差嘛 r = y − f m − 1 ( x ) r = y-f_{m-1}(x) r=y−fm−1(x) ,相当于每个新的弱分类器(准确来说,应该是基函数)都应该尽可能地去拟合残差
所以啊!!!!实际上一轮的提升树,本质上就是GBDT
不管,就先这么确定,以后打脸再说…好困
相关文章:

机器学习——boosting之GBDT
现在要开始重点关注名字了,名字透漏了很多信息!名字暗藏线索! GBDT,Gradient Boosting Decision Tree: 梯度提升决策树 果然信息很丰富 梯度:意味着计算有迭代递进关系,但还不明确是怎么迭代递进的 提升&…...

如何选择报修管理系统?报修工单管理系统有哪些功能和优势?
报修管理系统是一种能够帮助企业快速反应设备故障和异常情况,并将问题及时通知到相关人员,并对问题进行统计和分析的系统。它能够有效提高企业的工作效率,并减少人员成本的支出。那么,报修工单管理系统有哪些功能和优势呢?下面以“…...
Matlab图像处理-
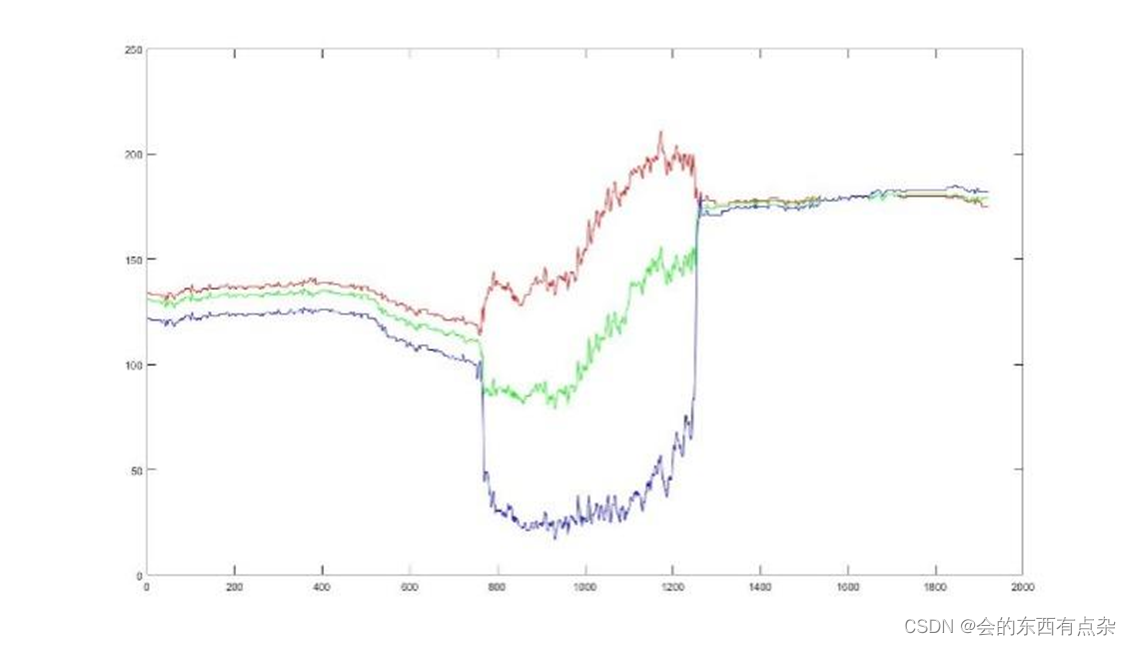
有些时候,直接利用图像的灰度直方图选择阈值不是非常直观,这时,可以利用图像三个通道的直方图来进行图像分割,操作步骤如上文所示,下图为原始图片。 下图为三通道直方图。 下图将三个通道的直方图会绘制到一个图表上&a…...
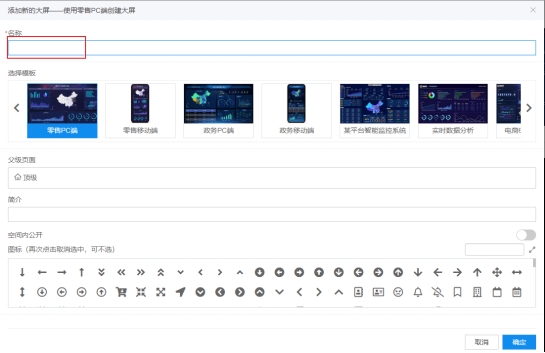
数据接口工程对接BI可视化大屏(二)创建BI空间
第2章 创建BI空间 2.1 SugarBI介绍 网站地址:https://cloud.baidu.com/product/sugar.html SugarBI是百度推出的自助BI报表分析和制作可视化数据大屏的强大工具。 基于百度Echarts提供丰富的图表组件,开箱即用、零代码操作、无需SQL,5分钟即可完成数…...

Struts.xml 配置文件说明
<?xml version"1.0" encoding"UTF-8" ?> <!DOCTYPE struts PUBLIC "-//Apache Software Foundation//DTD Struts Configuration 2.3//EN" "http://struts.apache.org/dtds/struts-2.3.dtd"> <struts> <!--…...
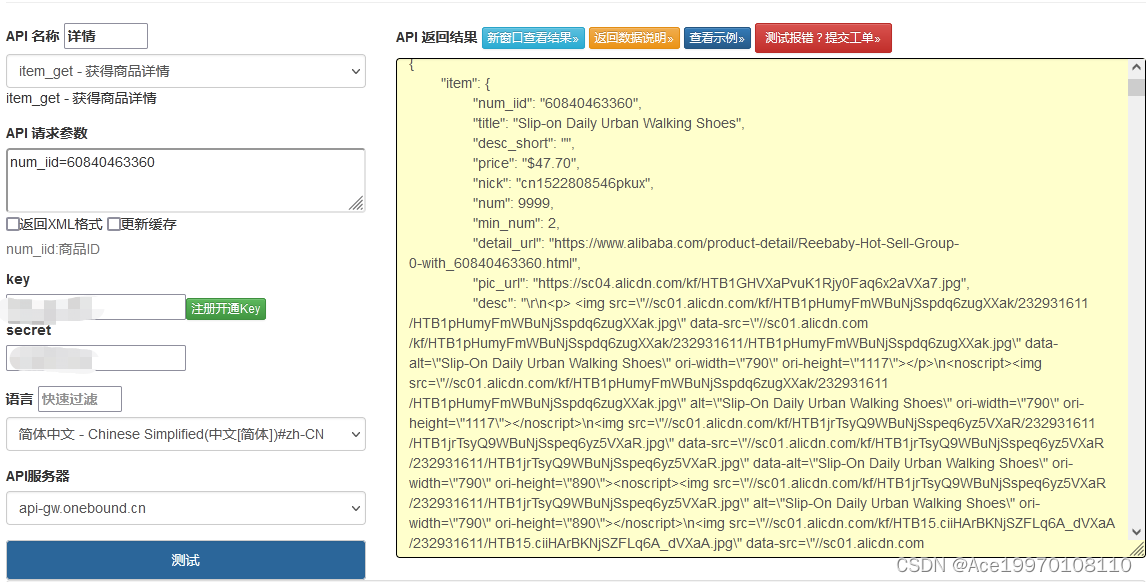
阿里巴巴API接口解析,实现获得商品详情
要解析阿里巴巴API接口并实现获取商品详情,你需要按照以下步骤进行操作: 了解阿里巴巴开放平台:访问阿里巴巴开放平台,并了解相关的API文档、开发者指南和规定。注册开发者账号:在阿里巴巴开放平台上注册一个开发者账…...
9.(Python数模)(分类模型一)K-means聚类
Python实现K-means聚类 K-means原理 K-means均值聚类算法作为最经典也是最基础的无标签分类学习算法。其实质就是根据两个数据点的距离去判断他们是否属于一类,对于一群点,就是类似用几个圆去框定这些点(簇),然后圆心…...
MinIO集群模式信息泄露漏洞(CVE-2023-28432)
前言:MinIO是一个用Golang开发的基于Apache License v2.0开源协议的对象存储服务。虽然轻量,却拥有着不错的性能。它兼容亚马逊S3云存储服务接口,非常适合于存储大容量非结构化的数据。该漏洞会在前台泄露用户的账户和密码。 0x00 环境配置 …...

【从零单排Golang】第十五话:用sync.Once实现懒加载的用法和坑点
在使用Golang做后端开发的工程中,我们通常需要声明一些一些配置类或服务单例等在业务逻辑层面较为底层的实例。为了节省内存或是冷启动开销,我们通常采用lazy-load懒加载的方式去初始化这些实例。初始化单例这个行为是一个非常经典的并发处理的案例&…...
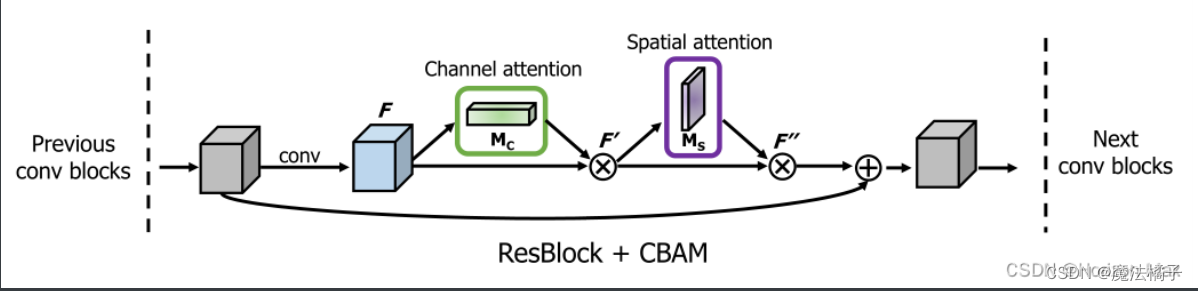
常见注意力机制
注意力机制 (具有自适应性) 18年提出的一种新的 卷积注意力模块 ;对前馈卷积神经网络 是一个 简单而有效的 注意力模块 ; 因为它的 轻量级和通用性 ,可以 无缝集成到任何CNN网络 当中, 对我们来讲&…...
解决报错之org.aspectj.lang不存在
一、IDEA在使用时,可能会遇到maven依赖包明明存在,但是build或者启动时,报找不存在。 解决办法:第一时间检查Setting->Maven-Runner红圈中的√有没有选上。 二、有时候,明明依赖包存在,但是Maven页签中…...

java之SpringBoot基础篇、前后端项目、MyBatisPlus、MySQL、vue、elementUi
文章目录 前言JC-1.快速上手SpringBootJC-1-1.SpringBoot入门程序制作(一)JC-1-2.SpringBoot入门程序制作(二)JC-1-3.SpringBoot入门程序制作(三)JC-1-4.SpringBoot入门程序制作(四)…...

golang中如何判断字符串是否包含另一字符串
golang中如何判断字符串是否包含另一字符串 在Go语言中,可以使用strings.Contains()函数来判断一个字符串是否包含另一个字符串。该函数接受两个参数:要搜索的字符串和要查找的子字符串,如果子字符串存在于要搜索的字符串中,则返…...

ONNX OpenVino TensorRT MediaPipe NCNN Diffusers ComfyUI
框架 和Java生成的中间文件可以在JVM上运行一样,AI技术在具体落地应用方面,和其他软件技术一样,也需要具体的部署和实施的。既然要做部署,那就会有不同平台设备上的各种不同的部署方法和相关的部署架构工具 onnx 在训练模型时可以…...
java中使用 Integer 和 int 的 含义、使用方法 及之间的区别
学习目标: 学习目标如下: 明确 Integer 和 int 的 含义、使用方法 及之间的区别 学习内容: 一、区别: 1.Integer是int的包装类,int则是java的一种基本的数据类型; 2.Integer变量必须实例化之后才能使用&a…...

点云从入门到精通技术详解100篇-点云的特征检测
目录 前言 点云配准的研究背景 多元时间序列的相似性分析研究背景及意义 国内外研究现状...

DOM破坏绕过XSSfilter例题
目录 一、什么是DOM破坏 二、例题1 编辑 三、多层关系 1.Collection集合方式 2.标签关系 四、例题2 一、什么是DOM破坏 DOM破坏(DOM Clobbering)指的是对网页上的DOM结构进行不当的修改,导致页面行为异常、性能问题、安全风险或其他不…...

代码随想录Day_56打卡
①、两个字符串的删除操作 给定两个单词 word1 和 word2 ,返回使得 word1 和 word2 相同所需的最小步数。 每步 可以删除任意一个字符串中的一个字符。 事例: 输入: word1 "sea", word2 "eat" 输出: 2 解释: 第一步将 "sea&…...

高忆管理:六连板捷荣技术或难扛“华为概念股”大旗
在本钱商场上名不见经传的捷荣技术(002855.SZ)正扛起“华为概念股”大旗。 9月6日,捷荣技术已拿下第六个连续涨停板,短短七个生意日,股价累积涨幅逾越90%。公司已连发两份股票生意异动公告。 是炒作,还是…...
「解析」YOLOv5 classify分类模板
学习深度学习有些时间了,相信很多小伙伴都已经接触 图像分类、目标检测甚至图像分割(语义分割)等算法了,相信大部分小伙伴都是从分类入门,接触各式各样的 Backbone算法开启自己的炼丹之路。 但是炼丹并非全是 Backbone,更多的是各…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...
