ABY2.0:更低的通信开销
参考文献:
- [ABY] Demmler D, Schneider T, Zohner M. ABY-A framework for efficient mixed-protocol secure two-party computation[C]//NDSS. 2015.
- [ABY3] Mohassel P, Rindal P. ABY3: A mixed protocol framework for machine learning[C]//Proceedings of the 2018 ACM SIGSAC conference on computer and communications security. 2018: 35-52.
- [ABY2.0] Patra A, Schneider T, Suresh A, et al. {ABY2. 0}: Improved {Mixed-Protocol} Secure {Two-Party} Computation[C]//30th USENIX Security Symposium (USENIX Security 21). 2021: 2165-2182.
- [Beaver91] D. Beaver. Effificient multiparty protocols using circuit randomization. In CRYPTO, 1991.
- [ALSM13] Asharov G, Lindell Y, Schneider T, et al. More efficient oblivious transfer and extensions for faster secure computation[C]//Proceedings of the 2013 ACM SIGSAC conference on Computer & communications security. 2013: 535-548.
- [RSS19] Rathee D, Schneider T, Shukla K K. Improved multiplication triple generation over rings via RLWE-based AHE[C]//International Conference on Cryptology and Network Security. Cham: Springer International Publishing, 2019: 347-359.
文章目录
- 混合 MPC
- 乘法协议
- ABY 转换
混合 MPC
首先汇总下以 Arithmetic - Boolean - Yao 为名的三种混合协议:
- 著名的 ABY 是第一个混合多种 MPC 协议的安全多方计算协议。不过由于 Yao’s GC 的限制,它仅仅是个半诚实安全的 2PC 协议。
- 之后的 ABY3 是一种恶意安全的 3PC 协议。它使用了 Yao’s GC 的三方扩展,两个 Garbler,一个 Evaluator。由于三方协议计算 AND 门不需要 Beaver Triple,因此计算速度比 ABY 快很多。
- 而 ABY2.0 则是对 ABY 的通信性能做了改进,它也是半诚实安全的 2PC 协议。
它们的基本流程都是:
- 利用 Sharing protocol,将输入值分享给各方
- 利用 SS 的 Linear Homomorphic 性质,以及 Multiplication protocol,计算给定的函数(期间做 A-B-Y 之间的 shares 转换)
- 使用 Reconstruction protocol,从 shares 恢复出输出值
乘法协议
使用 Beaver Triple 计算乘法门,给定元组 ( δ a , δ b , δ a b = δ a δ b ) (\delta_a,\delta_b,\delta_{ab}=\delta_a\delta_b) (δa,δb,δab=δaδb),满足关系
a b = ( a + δ a − δ a ) ( b + δ b − δ b ) = ( a + δ a ) ( b + δ b ) − ( a + δ a ) δ b − ( b + δ b ) δ a + δ a b \begin{aligned} ab &= (a+\delta_a-\delta_a)(b+\delta_b-\delta_b)\\ &= (a+\delta_a)(b+\delta_b) - (a+\delta_a)\delta_b - (b+\delta_b)\delta_a + \delta_{ab} \end{aligned} ab=(a+δa−δa)(b+δb−δb)=(a+δa)(b+δb)−(a+δa)δb−(b+δb)δa+δab
简记 Δ a = a + δ a , Δ b = b + δ b \Delta_a=a+\delta_a, \Delta_b=b+\delta_b Δa=a+δa,Δb=b+δb。参与方 P i , i ∈ { 0 , 1 } P_i,i\in \{0,1\} Pi,i∈{0,1} 持有 ( [ a ] i , [ δ a ] i ) , ( [ b ] i , [ δ b ] i ) , [ δ a b ] i ([a]_i, [\delta_a]_i),([b]_i, [\delta_b]_i), [\delta_{ab}]_i ([a]i,[δa]i),([b]i,[δb]i),[δab]i 这些 shares,为了计算 c = a b c=ab c=ab 的 shares,使用 Beaver 乘法协议:
- P i P_i Pi 计算 [ Δ a ] i = [ a ] i + [ δ a ] i [\Delta_a]_i = [a]_i+[\delta_a]_i [Δa]i=[a]i+[δa]i 以及 [ Δ b ] i = [ b ] i + [ δ b ] i [\Delta_b]_i = [b]_i+[\delta_b]_i [Δb]i=[b]i+[δb]i
- P i P_i Pi 互相发送 [ Δ a ] i [\Delta_a]_i [Δa]i 和 [ Δ b ] i [\Delta_b]_i [Δb]i 给对方(四个元素)
- P i P_i Pi 重构出 Δ a = [ Δ a ] 0 + [ Δ a ] 1 \Delta_a=[\Delta_a]_0+[\Delta_a]_1 Δa=[Δa]0+[Δa]1 和 Δ a = [ Δ a ] 0 + [ Δ a ] 1 \Delta_a=[\Delta_a]_0+[\Delta_a]_1 Δa=[Δa]0+[Δa]1
- P i P_i Pi 计算 [ c ] i = i ⋅ Δ a Δ b − Δ a [ δ b ] i − Δ b [ δ a ] i + [ δ a b ] i [c]_i = i \cdot \Delta_a\Delta_b - \Delta_a[\delta_b]_i - \Delta_b[\delta_a]_i + [\delta_{ab}]_i [c]i=i⋅ΔaΔb−Δa[δb]i−Δb[δa]i+[δab]i
- P i P_i Pi 持有了 [ c ] i [c]_i [c]i,容易验证 [ c ] 0 + [ c ] 1 = a b = c [c]_0+[c]_1=ab=c [c]0+[c]1=ab=c
ABY2.0 观察到 Δ a , Δ b \Delta_a,\Delta_b Δa,Δb 最终是明文信息,因此修改 shares 的格式,从原本的 ( [ a ] i , [ δ a ] i ) ([a]_i, [\delta_a]_i) ([a]i,[δa]i) 变为了 ( Δ a , [ δ a ] i ) (\Delta_a,[\delta_a]_i) (Δa,[δa]i)。容易验证:
a = Δ a − [ δ a ] 0 − [ δ a ] 1 c 1 ⋅ ( Δ a , [ δ a ] i ) + c 2 ⋅ ( Δ b , [ δ b ] i ) = ( Δ c 1 a + c 2 b , [ δ c 1 a + c 2 b ] i ) a = \Delta_a - [\delta_a]_0 - [\delta_a]_1\\ c_1 \cdot (\Delta_a,[\delta_a]_i) + c_2 \cdot (\Delta_b,[\delta_b]_i) = (\Delta_{c_1a+c_2b}, [\delta_{c_1a+c_2b}]_i) a=Δa−[δa]0−[δa]1c1⋅(Δa,[δa]i)+c2⋅(Δb,[δb]i)=(Δc1a+c2b,[δc1a+c2b]i)
因此定义 ⟨ a ⟩ i : = ( Δ a , [ δ a ] i ) \langle a\rangle_i := (\Delta_a,[\delta_a]_i) ⟨a⟩i:=(Δa,[δa]i) 是新的 shares 格式,它依然是线性同态的。它对应的 Sharing Protocol 为, P i P_i Pi 随机采样 [ δ a ] 0 , [ δ a ] 1 [\delta_a]_0,[\delta_a]_1 [δa]0,[δa]1,计算 Δ a = a + [ δ a ] 0 + [ δ a ] 1 \Delta_a=a+[\delta_a]_0+[\delta_a]_1 Δa=a+[δa]0+[δa]1,自己持有 ⟨ a ⟩ i = ( Δ a , [ δ a ] i ) \langle a\rangle_i = (\Delta_a,[\delta_a]_i) ⟨a⟩i=(Δa,[δa]i),将 ⟨ a ⟩ 1 − i = ( Δ a , [ δ a ] 1 − i ) \langle a\rangle_{1-i} = (\Delta_a,[\delta_a]_{1-i}) ⟨a⟩1−i=(Δa,[δa]1−i) 发送给对方。
参与方 P i , i ∈ { 0 , 1 } P_i,i\in \{0,1\} Pi,i∈{0,1} 持有 ( Δ a , [ δ a ] i ) , ( Δ b , [ δ b ] i ) , [ δ a b ] i (\Delta_a, [\delta_a]_i),(\Delta_b, [\delta_b]_i), [\delta_{ab}]_i (Δa,[δa]i),(Δb,[δb]i),[δab]i 这些 shares,为了计算 c = a b c=ab c=ab 的 shares,使用 ABY2.0 乘法协议:
- P i P_i Pi 独立生成随机数 [ δ c ] i [\delta_c]_i [δc]i(作为 Sharing 协议的一部分)
- P i P_i Pi 计算 [ Δ c ] i = i ⋅ Δ a Δ b − Δ a [ δ b ] i − Δ b [ δ a ] i + [ δ a b ] i + [ δ c ] i [\Delta_c]_i = i \cdot \Delta_a\Delta_b - \Delta_a[\delta_b]_i - \Delta_b[\delta_a]_i + [\delta_{ab}]_i + [\delta_c]_i [Δc]i=i⋅ΔaΔb−Δa[δb]i−Δb[δa]i+[δab]i+[δc]i
- P i P_i Pi 互相发送 [ Δ c ] i [\Delta_c]_i [Δc]i 给对方(两个元素)
- P i P_i Pi 重构出 Δ c = [ Δ c ] 0 + [ Δ c ] 1 \Delta_c = [\Delta_c]_0 + [\Delta_c]_1 Δc=[Δc]0+[Δc]1
- P i P_i Pi 持有了 ⟨ c ⟩ i = ( Δ c , [ δ c ] i ) \langle c \rangle_i = (\Delta_c, [\delta_c]_i) ⟨c⟩i=(Δc,[δc]i),容易验证 Δ c − [ δ c ] 0 − [ δ c ] 1 = a b = c \Delta_c-[\delta_c]_0-[\delta_c]_1=ab=c Δc−[δc]0−[δc]1=ab=c
Beaver 和 ABY2.0 对比如下:

上述的乘法协议在算术电路和布尔电路中都奏效,假设消息空间是 Z 2 l \mathbb Z_{2^l} Z2l,那么在 Online 阶段,ABY2.0 乘法门的通信开销仅为 2 l 2l 2l 比特,对比 Beaver 的开销为 4 l 4l 4l 比特。
对于 Setup 阶段,ABY2.0 的开销没变,因为它依然要生成 Beaver Triple。这可以通过 C-OT 或者 AHE 实现。
- 由于 δ a b = ( [ δ a ] 0 + [ δ a ] 1 ) ( [ δ b ] 0 + [ δ b ] 1 ) \delta_{ab} = ([\delta_a]_0+[\delta_a]_1)([\delta_b]_0+[\delta_b]_1) δab=([δa]0+[δa]1)([δb]0+[δb]1) 可以拆分出四项加和,其中两项 [ δ a ] i [ δ b ] i [\delta_a]_i[\delta_b]_i [δa]i[δb]i 可以本地计算,因此我们只需实现交叉项 [ δ a ] i [ δ b ] 1 − i [\delta_a]_i[\delta_b]_{1-i} [δa]i[δb]1−i 的 shares 计算。
- C-OT based [ALSM13],
- P i P_i Pi 作为发送方,定义相关函数 f j ( x ) = x + 2 j [ δ a ] i f_j(x)=x+2^j[\delta_a]_i fj(x)=x+2j[δa]i,输入 ( m j , 0 = r j , m j , 1 = f ( r j ) ) (m_{j,0}=r_j, m_{j,1}=f(r_j)) (mj,0=rj,mj,1=f(rj)),
- P 1 − i P_{1-i} P1−i 作为接收方,根据 [ δ b ] 1 − i [\delta_b]_{1-i} [δb]1−i 的第 j j j 比特 b j b_j bj 做出选择, 获得 m j , b j m_{j,b_j} mj,bj
- P i P_i Pi 持有 [ d ] i = − ∑ j r j [d]_i = -\sum_jr_j [d]i=−∑jrj, P 1 − i P_{1-i} P1−i 持有 [ d ] 1 − i = ∑ j m j , b j [d]_{1-i} = \sum_j m_{j,b_j} [d]1−i=∑jmj,bj,容易验证 [ d ] i + [ d ] 1 − i = [ δ a ] i [ δ b ] 1 − i [d]_i+[d]_{1-i} = [\delta_a]_i[\delta_b]_{1-i} [d]i+[d]1−i=[δa]i[δb]1−i
- AHE based [RSS19],
- P 0 P_0 P0 生成公钥 p k pk pk,将 [ δ a ] 0 , [ δ b ] 0 [\delta_a]_0, [\delta_b]_0 [δa]0,[δb]0 加密后发送给 P 1 P_1 P1
- P 1 P_1 P1 生成随机数 r r r,同态计算线性函数 v = [ δ a ] 0 [ δ b ] 1 + [ δ a ] 1 [ δ b ] 0 − r v = [\delta_a]_0[\delta_b]_1 + [\delta_a]_1[\delta_b]_0 - r v=[δa]0[δb]1+[δa]1[δb]0−r
- P 1 P_1 P1 发送密文 E ( v ) E(v) E(v), P 0 P_0 P0 解密得到 v v v
- P 0 P_0 P0 持有 [ d ] 0 = v [d]_0=v [d]0=v, P 1 P_1 P1 持有 [ d ] 1 = r [d]_1=r [d]1=r,容易验证 [ d ] 0 + [ d ] 1 = [ δ a ] 0 [ δ b ] 1 + [ δ a ] 1 [ δ b ] 0 [d]_0+[d]_1=[\delta_a]_0[\delta_b]_1 + [\delta_a]_1[\delta_b]_0 [d]0+[d]1=[δa]0[δb]1+[δa]1[δb]0
ABY 转换
ABY2.0 同时使用了 [ a ] i [a]_i [a]i 和 ⟨ a ⟩ i \langle a \rangle_i ⟨a⟩i 两种格式的 SS,因此 A-B-Y 之间的转换与 ABY 略有不同。不过基本思路是一样的,这里不再详细描述。

除了 Y2B,其他的转换 ABY2.0 的通信量更小。除了 A2B,其他的转换 ABY2.0 的通信轮数仅为 1 1 1。不过 ABY2.0 的初始化阶段通信开销会更大。
相关文章:

ABY2.0:更低的通信开销
参考文献: [ABY] Demmler D, Schneider T, Zohner M. ABY-A framework for efficient mixed-protocol secure two-party computation[C]//NDSS. 2015.[ABY3] Mohassel P, Rindal P. ABY3: A mixed protocol framework for machine learning[C]//Proceedings of the…...

vue项目预览图片
1.图片为本地上传的预览: <input type"file" ref"file"/> <img :src"imgUrl"/>let fr new FileReader()fr.readAsArrayBuffer(this.$refs.file.files[0])fr.addEventListener("loadend", (e) > {let buff…...
Tomcat 安装
1.关闭防火墙 2.安装JDK包 3. 4。添加环境变量 5.刷新配置文件 6.解压文件 7.启动tomcat 8. 9.编写tomcat.service文件 vim /etc/systemd/system/tomcat.service 10.刷新服务 11.打开浏览器访问:192.168.2.100:8080/,正常可以看到以下界面...

计算机网络的故事——HTTP报文内的HTTP信息
HTTP报文内的HTTP信息 文章目录 HTTP报文内的HTTP信息一、HTTP 报文二、请求报文及响应报文的结构三、编码提升传输速率 一、HTTP 报文 HTTP报文是由多行(CRLF作换行符)数据构成的字符串文本,HTTP报文可以分为报文首部和报文主体两部分&…...

CF1120 D. Power Tree 巧妙的图论转化
传送门 [前题提要]:无 题目描述: 就是给你一棵树,然后每个点有花费,然后你可以选一个点,付费后对这个点的子树的所有叶子结点增减任意权值. 考虑有一个人会给这棵树的所有叶子结点赋值(值我们不知道),输出最小的花费,使得无论它如何赋值,我们使用上述的花 费都能使所有的叶子…...
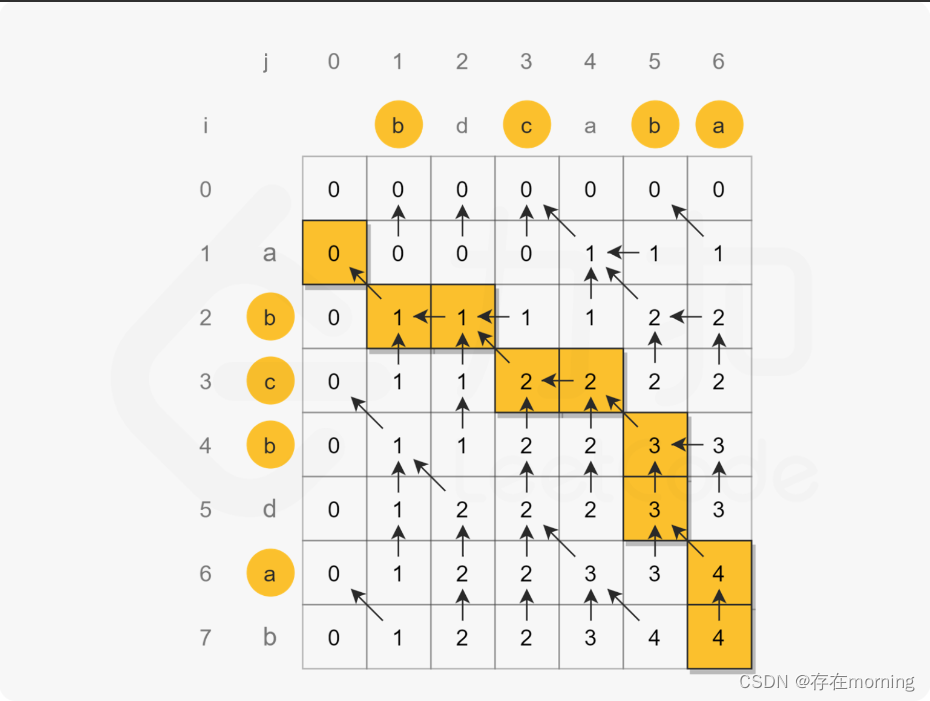
【算法训练-字符串 三】最长公共子串、最长公共子序列
废话不多说,喊一句号子鼓励自己:程序员永不失业,程序员走向架构!本篇Blog的主题是【】,使用【】这个基本的数据结构来实现,这个高频题的站点是:CodeTop,筛选条件为:目标公…...

lintcode 1446 · 01矩阵走路问题 【两次BFS, VIP 中等 1也计算距离,但是不入队列】
题目链接,描述 https://www.lintcode.com/problem/1446 给定一个大小为 n*m 的 01 矩阵 grid ,1 是墙,0 是路,你现在可以把 grid 中的一个 1 变成 0,请问从左上角走到右下角是否有路可走?如果有路可走&am…...
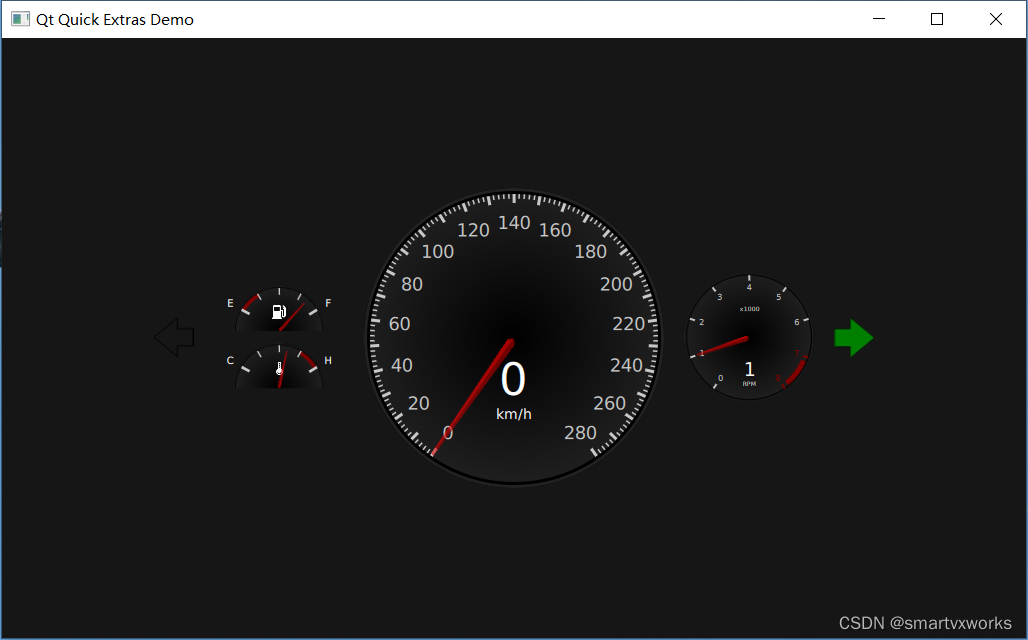
第一个实例:QT实现汽车电子仪表盘
目录 1.实现效果 1.1.视频演示 1.2.实现效果截图 2.生成的安装程序 3.功能概述 4.具体实现 5.QT扩展介绍 5.1.QT介绍 5.2.QT历史发展 5.3.QT平台支持 5.4.Qt Creator 5.5.优势 5.5.1.优良的跨平台特性 5.5.2.面向对象 5.5.3.丰富的 API 1.实现效果 1.1.视频演…...
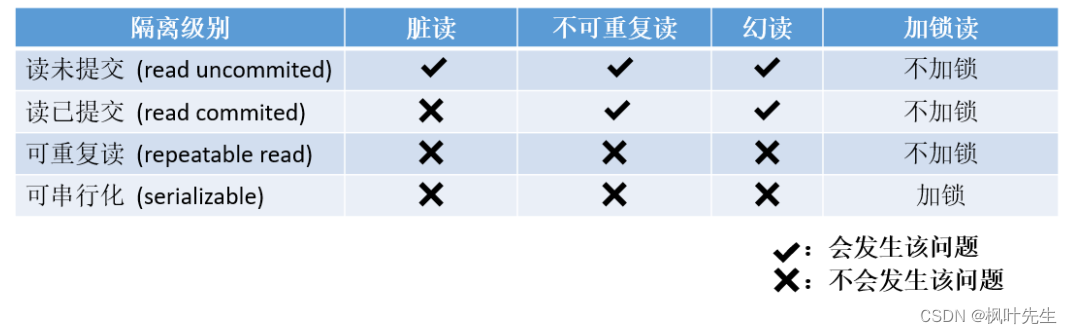
【MySQL系列】MySQL的事务管理的学习(一)_ 事务概念 | 事务操作方式 | 事务隔离级别
「前言」文章内容大致是MySQL事务管理。 「归属专栏」MySQL 「主页链接」个人主页 「笔者」枫叶先生(fy) 目录 一、事务概念二、事务的版本支持三、事务提交方式四、事务常见的操作方式4.1 事务正常操作4.2 事务异常验证 五、事务隔离级别5.1 查看与设置隔离性5.2 读未提交&…...

扫地机器人还能创新吗?云鲸给了个Yes
作者 | 辰纹 来源 | 洞见新研社 1996年,瑞典家电巨头伊莱克斯推出全球首款扫地机器人“三叶虫”。 与现在的产品相比,“三叶虫”靠随机碰撞的模式对空间进行清扫,清洁效率很低,市场渗透率也不高,但并不妨碍戴森、iRo…...
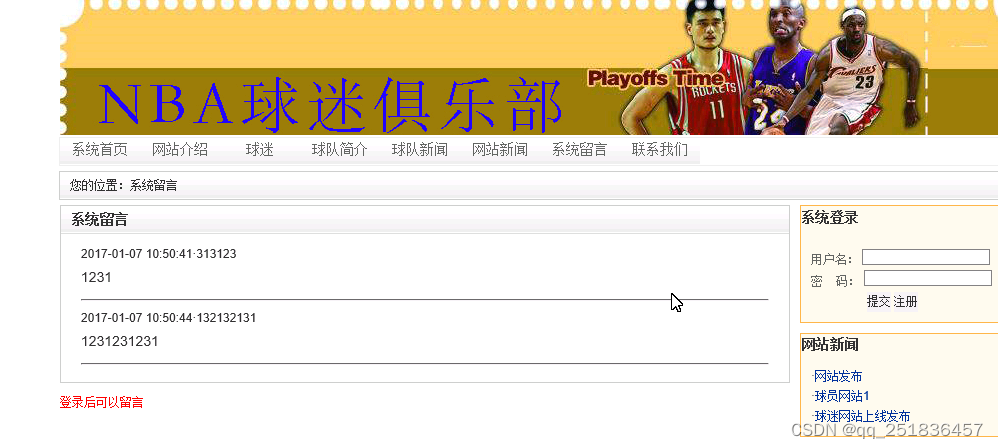
PHP NBA球迷俱乐部系统Dreamweaver开发mysql数据库web结构php编程计算机网页
一、源码特点 PHP NBA球迷俱乐部系统是一套完善的web设计系统,对理解php编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。 基于PHP的NBA球迷俱乐部 二、功能介绍 1、前台主要功能: 系统首页 网站介…...

JavaScript-----DOM元素
目录 前言: 1. DOM介绍 2. 获取节点 3. 操作HTML内容 4. 监听事件 案例 5. 操作节点的标签属性 6. 操作样式 7. 创建、添加、删除节点 前言: 在此之前我们要想去操作网页元素一般是去通过CSS选择器实现的,今天我们就学习JavaScript里…...

激光切割机在船舶行业的的应用有哪些
我国享有世界工厂的美誉,是全球制造业的主力。然而,在船舶制造的关键技术领域,我国的研发投入不足,技术进步仍滞后,我国高端船舶制造的实力仍显不足。 在我国制造业全面复苏的当前背景下,“精准制作”正构成…...
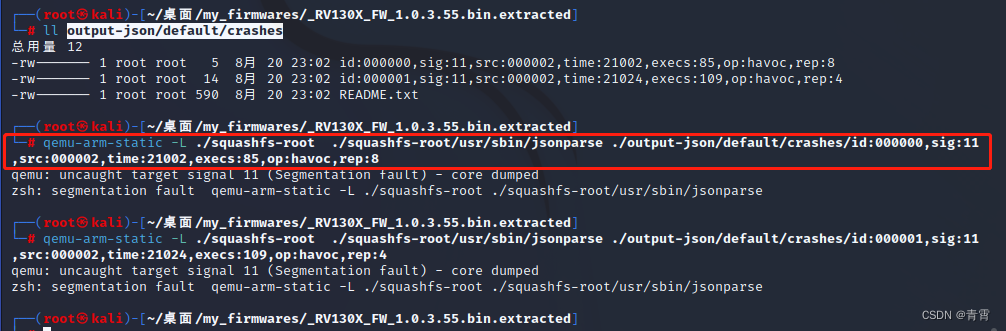
AFL++模糊测试
一、AFL 这里我们主要使用AFL Fuzzing 测试IOT的二进制文件,当我们解压提取一个固件时,能够获得大量的IOT二进制应用 ,如果要进行漏洞挖掘则需要将二进制文件进行逆向分析,然后查找危险函数以及输入接口,对于一个大型的…...

C# 使用ListBox及Picturebox显示所选的任意路径文件夹下的图像
using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; using System.Drawing; using System...

数据库: 存储过程
sql server begin end用法: SQL Server中的BEGIN END用法是用于定义一个代码块,这个代码块可以包含多个SQL语句,BEGIN END通常用于控制流程语句,例如IF语句、WHILE语句、TRY CATCH语句等。在BEGIN END代码块中,可以使用变量、函数…...
【juc】ReentrantReadWriteLock之缓存(仅当学习)
目录 一、说明二、代码示例2.1 pom依赖2.2 示例代码2.3 实体类 三、示例截图 一、说明 1.针对于读多写少的情况 2.先查缓存,没有再去查库 二、代码示例 2.1 pom依赖 <?xml version"1.0" encoding"UTF-8"?> <project xmlns"h…...

FLUX查询InfluxDB -- InfluxDB笔记三
1. 入门 from(bucket: "example_query") // 没有筛选条件直接查询会报错|> range(start: -1h) // |>是管道符,后跟筛选条件 2. 序列、表和表流 序列是InfluxDB的概念,一个序列是由measurement、标签集、一个字段名称 表流是FLUX为了…...
pico学习进程记录已经开发项目
Pico pin脚定义 Pico 运行准备 下载uf2文件 https://pico.org.cn/ (注意运行micropython的文件和运行c/c的不一样) 装载uf2文件:按住pico的按键,然后通过micro usb连接电脑(注意:如果用的线材,…...
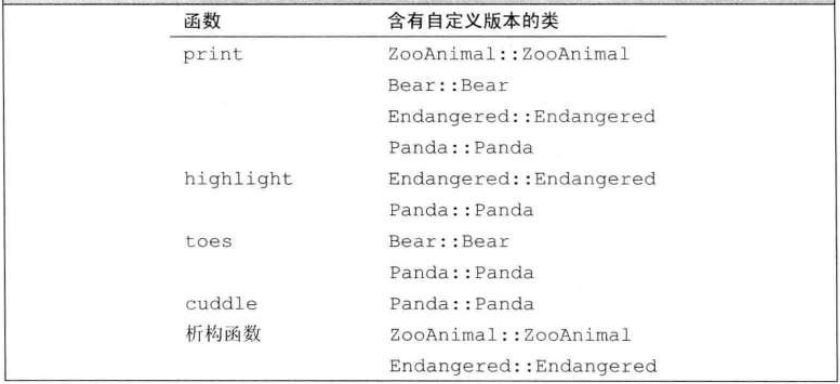
C++(20):多重继承与虚继承
多重继承 是指从多个直接基类中产生派生类的能力。多重继承的派生类继承了所有父类的属性。 多重继承 在派生类的派生列表中可以包含多个基类: class Bear : public zooAnimal { class Panda : public Bear, public Endangered{/* ...*/};每个基类包含一个可选的…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

【MATLAB代码】基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),附源代码|订阅专栏后可直接查看
文章所述的代码实现了基于最大相关熵准则(MCC)的三维鲁棒卡尔曼滤波算法(MCC-KF),针对传感器观测数据中存在的脉冲型异常噪声问题,通过非线性加权机制提升滤波器的抗干扰能力。代码通过对比传统KF与MCC-KF在含异常值场景下的表现,验证了后者在状态估计鲁棒性方面的显著优…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...

云安全与网络安全:核心区别与协同作用解析
在数字化转型的浪潮中,云安全与网络安全作为信息安全的两大支柱,常被混淆但本质不同。本文将从概念、责任分工、技术手段、威胁类型等维度深入解析两者的差异,并探讨它们的协同作用。 一、核心区别 定义与范围 网络安全:聚焦于保…...

基于开源AI智能名片链动2 + 1模式S2B2C商城小程序的沉浸式体验营销研究
摘要:在消费市场竞争日益激烈的当下,传统体验营销方式存在诸多局限。本文聚焦开源AI智能名片链动2 1模式S2B2C商城小程序,探讨其在沉浸式体验营销中的应用。通过对比传统品鉴、工厂参观等初级体验方式,分析沉浸式体验的优势与价值…...
