华为云 存在不支持迁移的外键解决方法
DRS 检测出源端存在不支持的外键引用操作
MySQL、GaussDB(for MySQL)为源的全量+增量或增量迁移、同步场景,以及MySQL、GaussDB(for MySQL)为源灾备场景
| 预检查项 | 源端存在不支持的外键引用操作。 |
|---|---|
| 描述 | 同步对象中存在包含CASCADE、SET NULL、SET DEFAULT之类引用操作的外键。这些关联操作会导致更新或删除父表中的行会影响子表对应的记录,并且子表的相关操作并不记录binlog。导致DRS无法同步,子表数据存在不一致。 |
| 不通过提示及处理建议 | 不通过原因:同步对象中存在包含CASCADE、SET NULL、SET DEFAULT之类引用操作的外键。这些关联操作会导致更新或删除父表中的行会影响子表对应的记录,并且子表的相关操作并不记录binlog。导致DRS无法同步,子表数据存在不一致。 处理建议:建议删除子表中包含CASCADE、SET NULL、SET DEFAULT之类引用操作的外键约束,或者不同步相关子表。 删除外键约束的参考语句: ALTER TABLE 表名 DROP FOREIGN KEY 外键名; |
相关文章:

华为云 存在不支持迁移的外键解决方法
DRS 检测出源端存在不支持的外键引用操作 MySQL、GaussDB(for MySQL)为源的全量增量或增量迁移、同步场景,以及MySQL、GaussDB(for MySQL)为源灾备场景 表1 源端存在不支持的外键引用操作 预检查项 源端存在不支持的外键引用操作。 描述 同步对象中存在包含CASC…...

Linux 中的 cd 命令及示例
cd命令在Linux 中称为更改目录命令。它用于有效地从当前工作目录移动到系统中的不同目录。 Linux 中 `cd` 命令的语法 光盘[目录] cd [directory]在这里,将 [directory] 替换为您要导航到的目标目录的路径。 “cd”命令的实际实现与示例。...

【VUE】
概念 VUE是一个用于构建用户界面的渐进式框架 构建用户界面:基于数据渲染出用户看到的界面 渐进式:声明式渲染->组件系统->客户端路由->大规模状态管理->构建工具 框架:一套完整的项目解决方案 VUE使用方式: 1.…...
详解初阶数据结构之顺序表(SeqList)——单文件文件实现SeqList的增删查改
目录 一、线性表 二、顺序表 2.1概念及结构 2.2接口实现 2.3动态顺序表的创建 2.3动态顺序表的初始化 2.3.1传值初始化 2.3.2传址初始化 2.4动态顺序表的清空 2.5动态顺序表的扩容 2.6动态顺序表内容的打印 三、动态顺序表的使用 3.1尾插尾删 3.1.1尾插 3.1.2尾删…...

JavaScript中的深拷贝和浅拷贝
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 浅拷贝(Shallow Copy):⭐深拷贝(Deep Copy):⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带…...

树形结构的节点作为查询参数业务
1、业务描述 有一个树结构,存在一个唯一的code和一个父节点的pcode,要求前端传入任意层的code匹配这个code对应的所有子节点对应的数据。 2、解决思路 因为无法判定传入的code到底在那层,so 直接递归调用查询判断,如果有子节点就…...
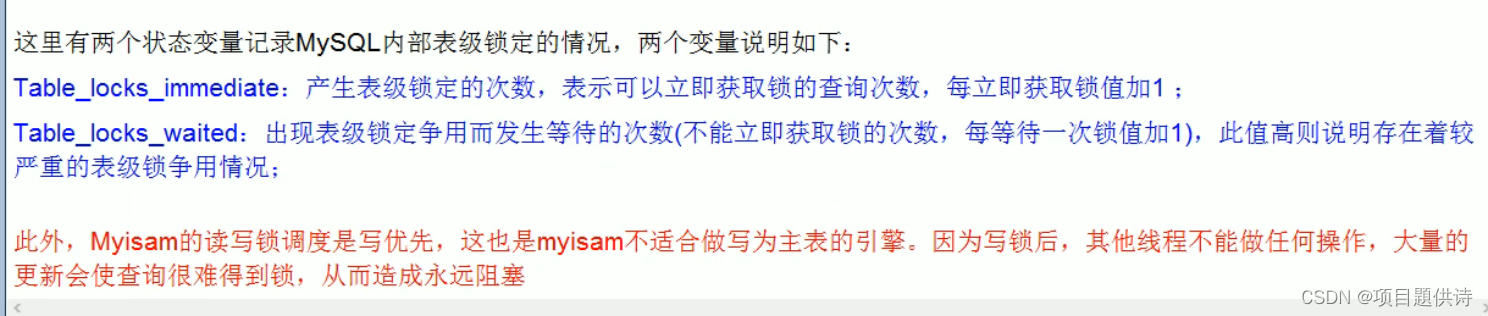
sql:SQL优化知识点记录(十二)
(1)读锁案例讲解 加读锁和写锁 查看是否上锁:In_use:变成了1 读写锁对我们数据产生哪些影响: 读锁:是共享锁,其他线程可以查看: 加了读锁:session1不能修改自己…...
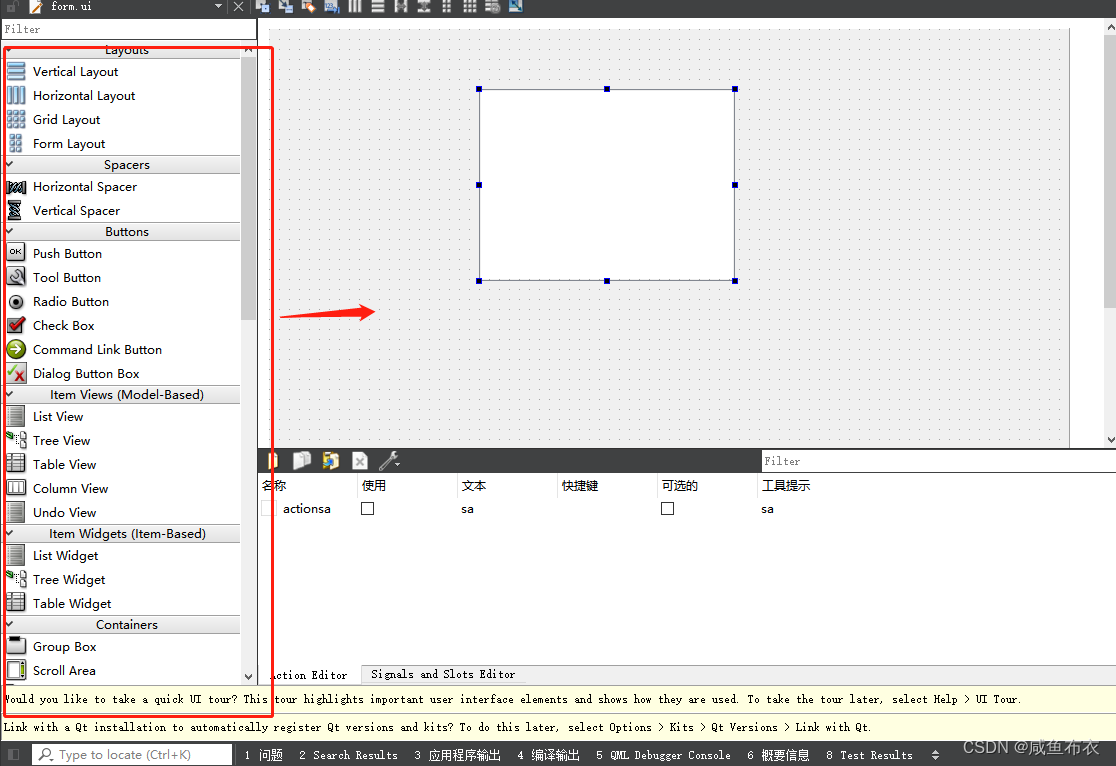
一.使用qt creator 设计显示GUI
一.安装qt creator 二.创建项目 文件-》新建项目 三.使用设计 可以直接使用鼠标拖拽 四.转换为py文件 # from123.py 为导出 py文件的文件名 form.ui 为 qt creator创造的 ui 文件 pyuic5 -o x:\xxx\from123.py form.ui五.显示GUI from PyQt5.QtWidgets import * fr…...

sql:SQL优化知识点记录(八)
(1)索引面试题分析 所谓索引:就是排好序的快速查找数据结构,排序家查找是索引的两个用途 select * 在where使用到了索引,当select * 有模糊查询%在左边索引会失效 当select * where后面索引的顺序发生变化࿰…...

java笔试题,寻找多出来的元素
题目:有两个数组a和b,其中b有一个元素是a没有的,其他元素都相同,请找出b中这个多余的元素。 1 public class Test02 { 2 3 public static void main(String[] args) { 4 int[] a {11, 34, 9, -4, 100, 98}; 5 int[] b {34…...
docker笔记3 Docker常规安装
1.安装tomcat docker hub上面查找tomcat镜像 docker search tomcat 从docker hub上拉取tomcat镜像到本地 docker pull tomcat docker images查看是否有拉取到的tomcat 使用tomcat镜像创建容器实例(也叫运行镜像) docker run -it -p 8080:8080 tomcat -p 小写,主…...
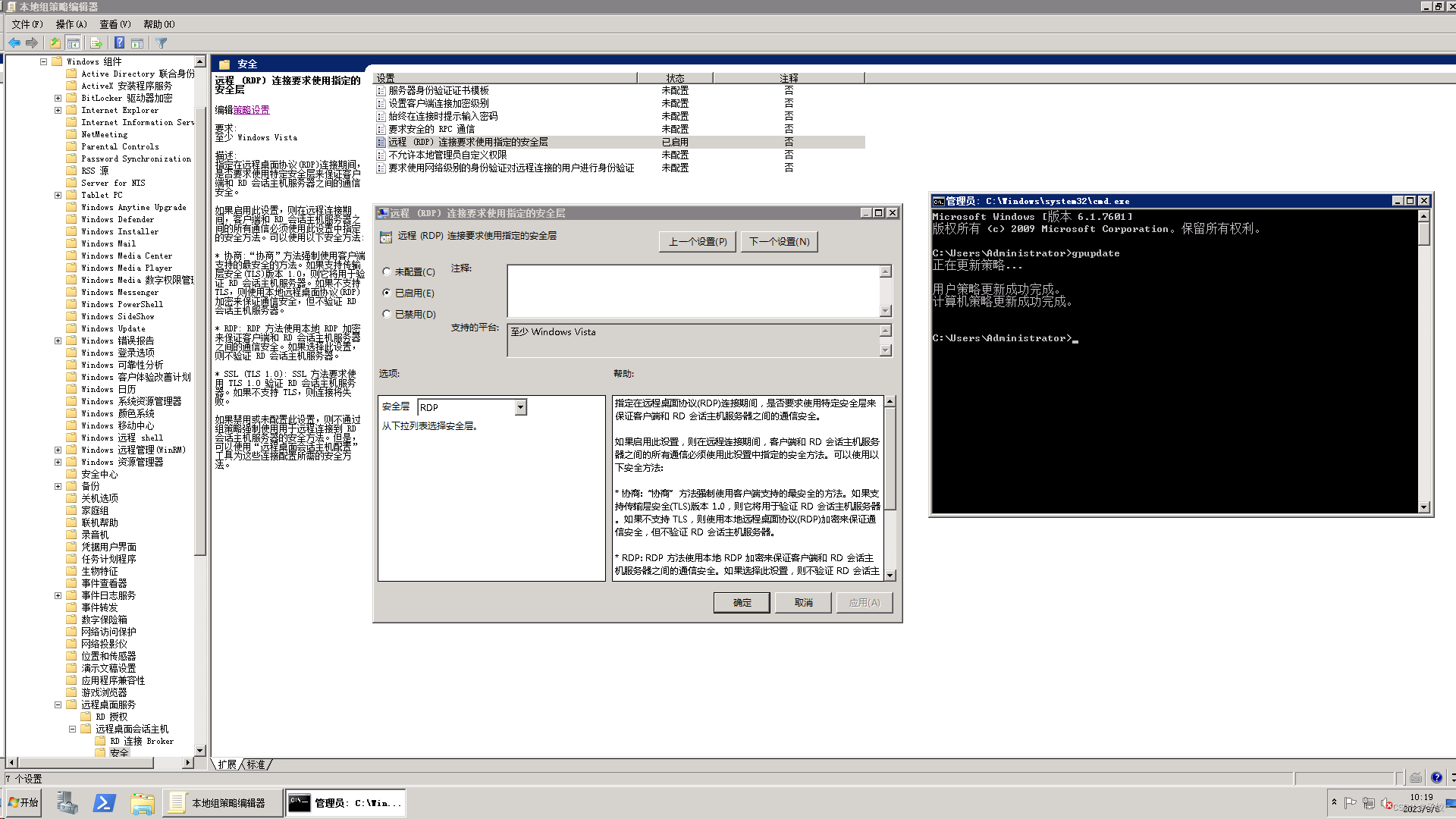
阻止 NTLM后无法登录远程桌面的原因
阻止 NTLM(NT LAN Manager) 攻击设置二 之前郑州景安的服务器被攻击,没过几天阿里云的也被攻击,且都是 NTLM 攻击。 Operating System: Windows Server 2008(R2) Enterprise Service Pack 1 64bit 一、winr 输入 gpedit.msc 二、依次进入:…...
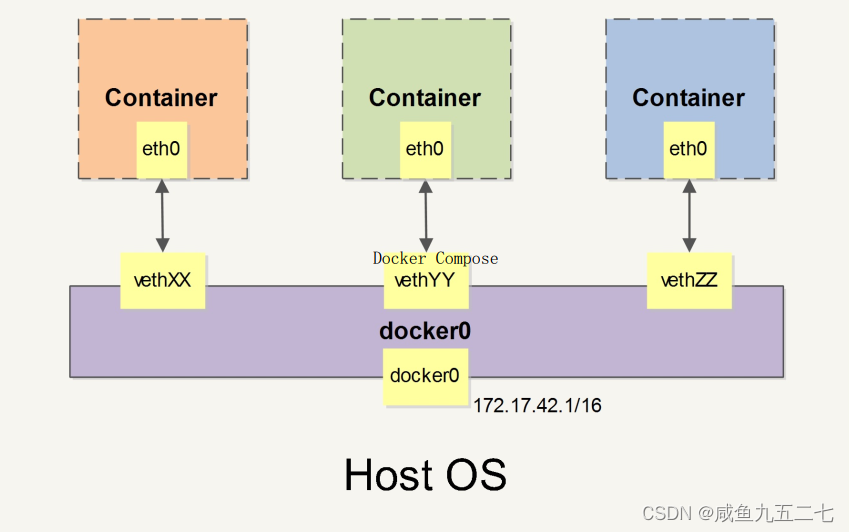
Docker网络功能
基本网络功能 Docker 允许通过外部访问容器或容器互联的方式来提供网络服务。使用docker network子命令来管理Docker网络。 外部访问容器可通过端口映射实现,启动容器时使用-p参数指定映射关系。-p可多次使用来绑定多个端口。使用docker port命令查看当前映射的端…...

如何入门 AI----如何确定学习目标
当确定学习人工智能(AI)的目标时,可以考虑以下具体的步骤: 兴趣和好奇心: 首先,问问自己,您对哪些 AI 领域感兴趣?是机器学习、自然语言处理、计算机视觉,还是其他领域&a…...

ABAP中加前导零和去前导零方法
文章目录 1 Introduction2 Method 1 Introduction In the sap there are two method for leading zero. We can use function or use the below the method . 2 Method SELECT * INTO TABLE DATA(IT_ITEM)FROM MARA .LOOP AT IT_ITEM ASSIGNING FIELD-SYMBOL(<FS_DATA&g…...

聊聊ShardingSphere是怎么进行sql重写的
序 本文主要研究一下ShardingSphere进行sql重写的原理 prepareStatement org/apache/shardingsphere/driver/jdbc/core/connection/ShardingSphereConnection.java public final class ShardingSphereConnection extends AbstractConnectionAdapter {Overridepublic Prepar…...

软件设计模式系列之二——抽象工厂模式
1 抽象工厂模式的定义 抽象工厂模式是一种创建型设计模式,它提供了一种创建一组相关或相互依赖对象的方式,而无需指定它们的具体类。该模式以一组抽象接口为核心,包括抽象工厂接口和一组抽象产品接口,每个具体工厂类负责创建特定…...

P2719 搞笑世界杯 (期望dp
#include <bits/stdc.h> using namespace std; using VI vector<int>;double dp[2000][2000]; int n; //求dp[2][0] //dp[0][2] //期望dp要从终末态,向起始态转移 //dp[a][b] - > dp[a][b-1] or dp[a-1][b] //dp[a][b] 1/2 * dp[a][b1] 1/2 * dp…...

spring cloud新版本使用loadbalancer替代Ribbon
Nacos 2021 不再集成 Ribbon,建议使用spring cloud loadbalancer 引入 一、简单使用 引入依赖spring cloud loadbalancer <dependency><groupId>org.springframework.cloud</groupId><artifactId>spring-cloud-starter-loadbalancer<…...

【Git-Exception】Git报错:fatal: unable to auto-detect email address
报错信息: *** Please tell me who you are. Run git config --global user.email “youexample.com” git config –global user.name “Your Name” to set your account’s default identity. Omit --global to set the identity only in this repository. fatal…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...
