【每日一题】补档 ABC309F - Box in Box | 三维偏序 | 树状数组 | 中等
题目内容
原题链接
给定 n n n 个箱子,问是否存在一个箱子 x x x 是否可以放到另一个箱子 y y y 里。
需要满足 h x < h y , w x < w y , d x < d y h_x<h_y,w_x<w_y,d_x<d_y hx<hy,wx<wy,dx<dy。
箱子可以随意翻转。
数据范围
1 ≤ n ≤ 2 ⋅ 1 0 5 1\leq n\leq 2\cdot 10^5 1≤n≤2⋅105
1 ≤ h i , w i , d i ≤ 1 0 9 1\leq h_i,w_i,d_i\leq 10^9 1≤hi,wi,di≤109
题解
首先按从小到大对 h , w , d h,w,d h,w,d 进行排序。
这里假设对所有的箱子,排序后都有 h ≤ w ≤ d h\leq w\leq d h≤w≤d
那么我们再按照 h h h 为第一关键字, w w w 为第二关键字, d d d 为第三关键字对箱子进行从小到大的排序。
然后我们从按 h h h 从小到大枚举,每次将所有 h h h 相同的箱子一起枚举。
这样,我们就可以对剩下的 w w w 和 d d d 构建树状数组了。
对于箱子 i i i ,找到 h j < h i h_j<h_i hj<hi 的 j j j ,且 w j < w i w_j<w_i wj<wi 的最小的 d j d_j dj 。判断 d j < d i d_j < d_i dj<di 是否成立即可。
然后在判断完后,将所有值为 h i h_i hi 的箱子都加入到树状数组中。
如 q u e r y ( p ) query(p) query(p) 其实是在求 w ≤ p w\leq p w≤p 的最小的 d d d 。
这个问题又叫三维偏序。
时间复杂度: O ( n log n ) O(n\log n) O(nlogn)
代码
#include <bits/stdc++.h>
using namespace std;const int INF = 0x3f3f3f3f;struct Node {int a[3];
};int main()
{ios::sync_with_stdio(false);cin.tie(nullptr);int n;cin >> n;vector<Node> vec(n);for (int i = 0; i < n; ++i) {for (int j = 0; j < 3; ++j) cin >> vec[i].a[j];sort(vec[i].a, vec[i].a + 3);}sort(vec.begin(), vec.end(), [](const Node& A, const Node& B) {return A.a[0] < B.a[0];});vector<int> b;for (int i = 0; i < n; ++i) b.push_back(vec[i].a[1]);sort(b.begin(), b.end());b.erase(unique(b.begin(), b.end()), b.end());auto get = [&](int x) {return int(lower_bound(b.begin(), b.end(), x) - b.begin() + 1);};for (int i = 0; i < n; ++i) vec[i].a[1] = get(vec[i].a[1]);int m = int(b.size());vector<int> tr(m + 1, INF);auto update = [&](int p, int x) {while (p <= m) {tr[p] = min(tr[p], x);p += (p & -p);}};auto query = [&](int p) {int res = INF;while (p >= 1) {res = min(res, tr[p]);p -= (p & -p);}return res;};bool ok = false;for (int i = 0; i < n; ++i) {int j = i + 1;while (j < n && vec[j].a[0] == vec[i].a[0]) j += 1;// 找到是否存在这么一个即可for (int k = i; k < j; ++k) {if (query(vec[k].a[1] - 1) < vec[k].a[2]) {ok = true;break;}}if (ok) break;// 把当前的部分全部添加进去for (int k = i; k < j; ++k) {update(vec[k].a[1], vec[k].a[2]);}i = j - 1;}if (ok) cout << "Yes\n";else cout << "No\n";return 0;
}
相关文章:

【每日一题】补档 ABC309F - Box in Box | 三维偏序 | 树状数组 | 中等
题目内容 原题链接 给定 n n n 个箱子,问是否存在一个箱子 x x x 是否可以放到另一个箱子 y y y 里。 需要满足 h x < h y , w x < w y , d x < d y h_x<h_y,w_x<w_y,d_x<d_y hx<hy,wx<wy,dx<dy。 箱子可以随意翻转。 …...

异步编程 - 13 高性能线程间消息传递库 Disruptor
文章目录 Disruptor概述Disruptor中的核心术语Disruptor 流程图 Disruptor的特性详解基于Disruptor实现异步编程 Disruptor概述 Disruptor是一个高性能的线程间消息传递库,它源于LMAX对并发性、性能和非阻塞算法的研究,如今构成了其Exchange基础架构的核…...
(DXE_DRIVER)PciHostBridge
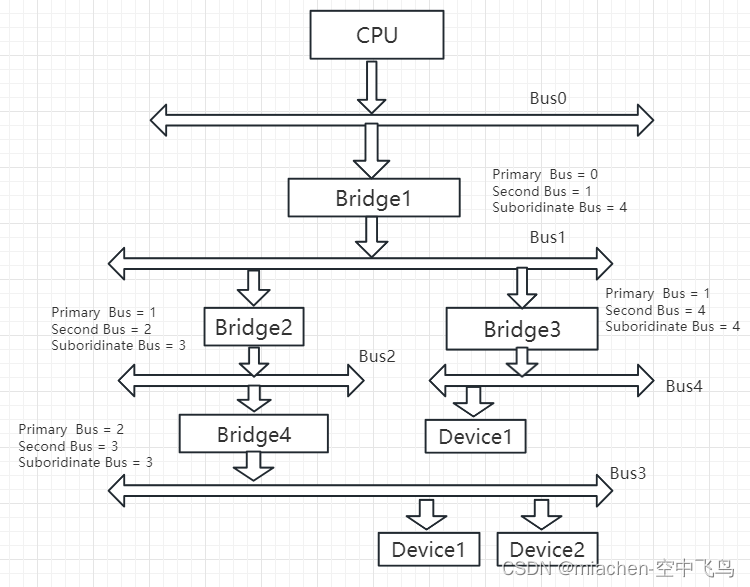
UEFI-PciHostBridge 1、PciHostBridge简介 PciHostBridge: 提供PCI配置空间,IO,MEM空间访问接口以及统一维护平台相关的PCI资源,提供gEfiPciHostBridgeResourceAllocationProtocolGuid,创建RootBridge等为PciBusDxe提供服务; 2、PciHostBridge 配置空间 PCI桥可管理其下PCI子…...
SpringMVC的增删改查的案例
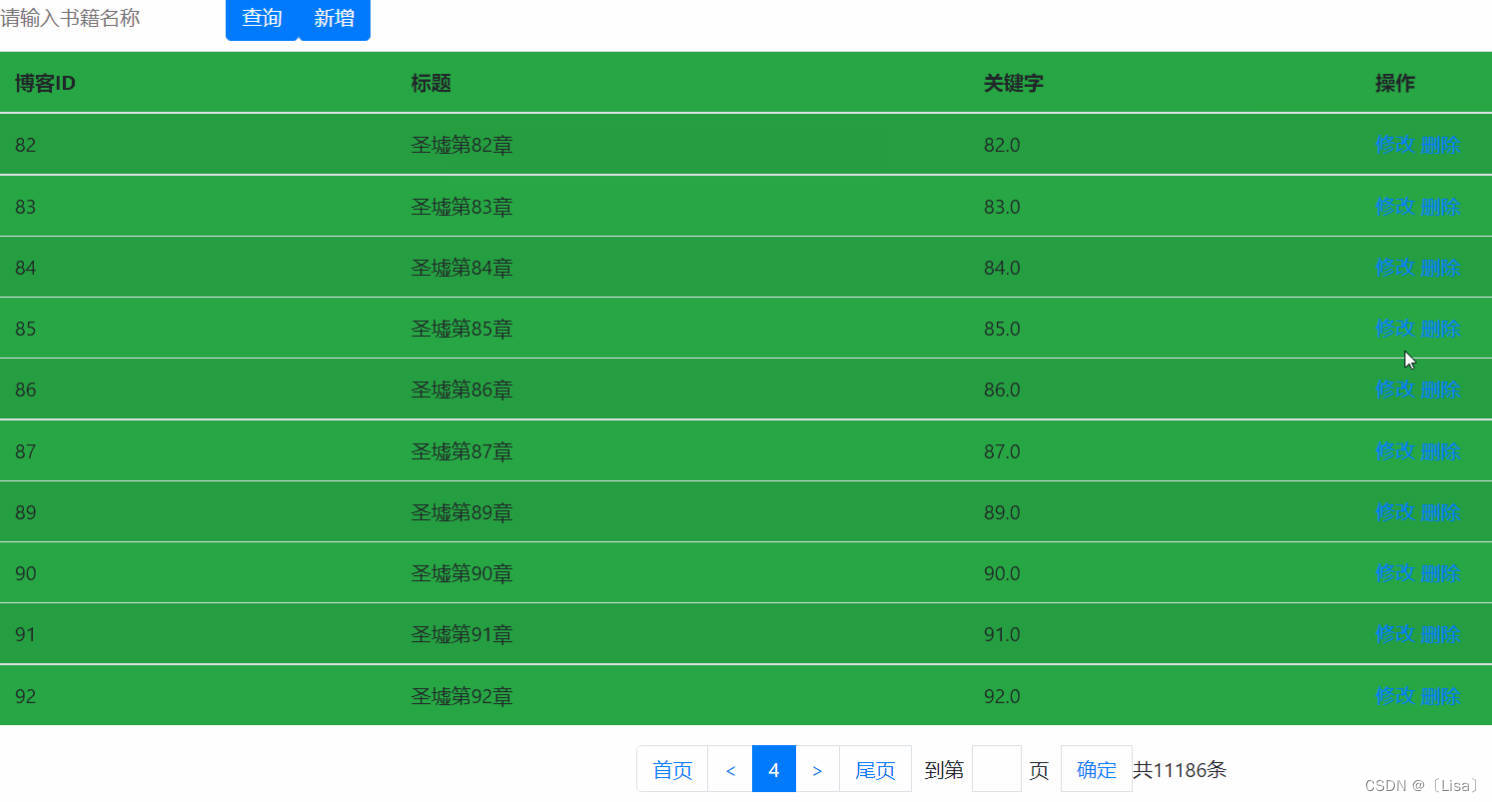
目录 前言: 1.总体思路: 2.前期准备 3.前台页面 前言: 我们今天来学习研究SpringMVC的增删改查,希望这篇博客能够帮助正在学习,工作的你们!!! 1.总体思路: 首先我们得…...
golang入门笔记——nginx
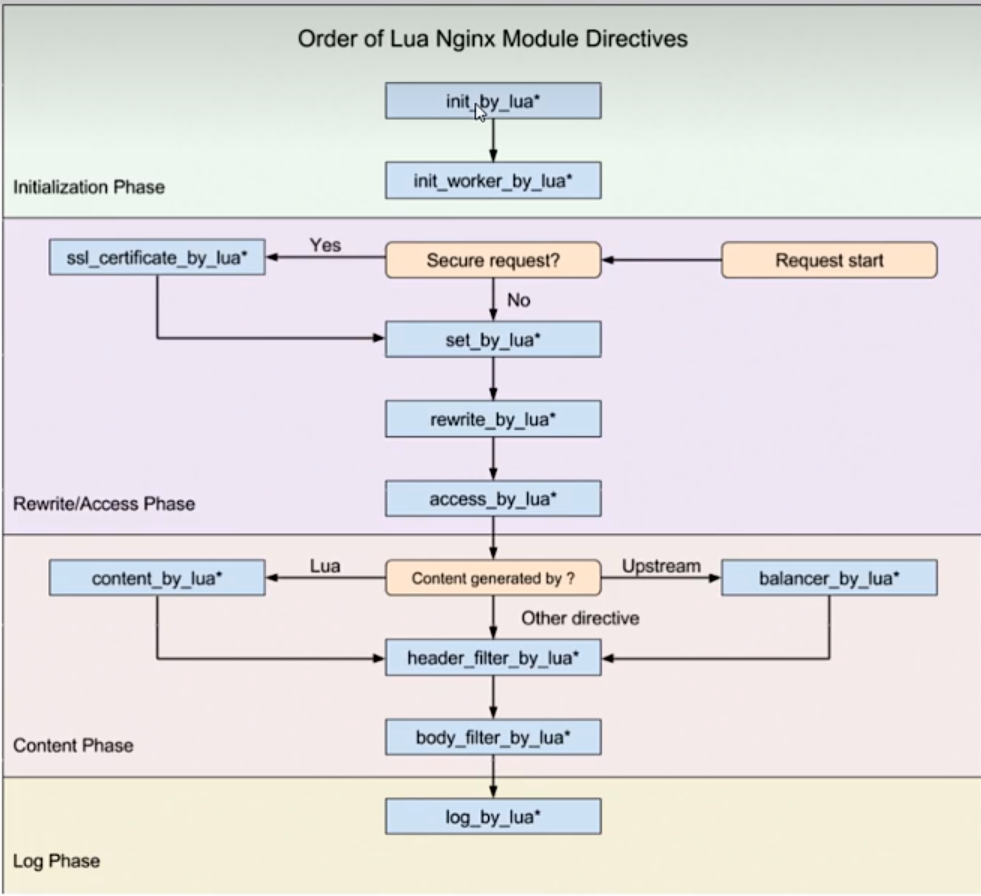
文章目录 Nginx介绍Nginx的安装Nginx文件Nginx反向代理负载均衡nginx动静分离URLRewrite防盗链nginx高可用配置安全性Nginx限流Nginx缓存集成Lua脚本OpenRestry Nginx介绍 Nginx是一个高性能的HTTP和反向代理服务器,特点是占用内存少,并发能力强&#x…...
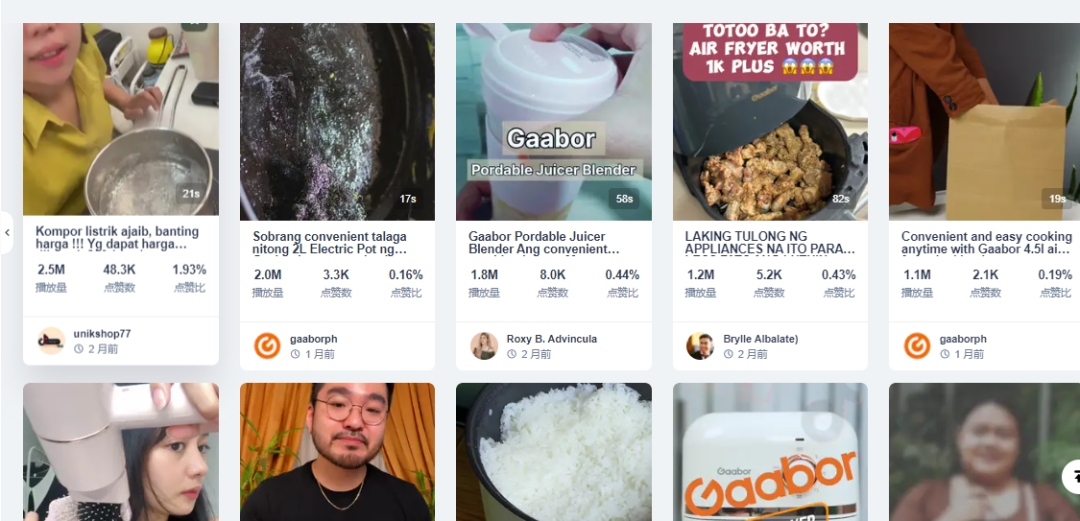
最新报告!TikTok 市场小家电大商机,GMV破亿的爆款如何复制?
近期,新锐小家电品牌Gaabor空气炸锅在东南亚卖爆了,单款商品GMV短时间内突破两亿,在印尼、泰国、马来西亚、菲律宾、越南均开设本土TikTok 小店,增长势头还在持续。 但Gaabor并不是个例。 整个东南亚家电市场规模增长迅速&#…...

功能定义-紧急制动系统
功能简介 紧急制动系统的触发过程如上图所示: 安全距离报警:当两车距离较近时,会给予驾驶员相应提示 预报警:当两车存在碰撞风险但风险较低【Danger Level1】时,会给予驾驶员提示【提示相比之前更为明显】 制动预填充&…...

Map与Set的区别
map与set是一种进行搜索的数据结构。 一 Map map存储的是key-value的键值对。 1 map中的常见方法 方法作用put(key,value)向map中存放key-value键值对get(key)根据key值得到value值getOrDefault(key,value)获取值为key的value,若不存在,则将key值对应…...
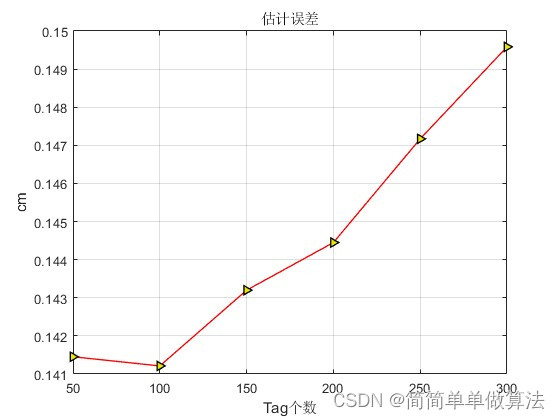
基于uwb和IMU融合的三维空间定位算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 ..........................................................................kkk 0; for E…...
Visual Studio 2019下使用C++与Python进行混合编程——环境配置与C++调用Python API接口
前言 在vs2019下使用C与Python进行混合编程,在根源上讲,Python 本身就是一个C库,那么这里使用其中最简单的一种方法是把Python的C API来嵌入C项目中,来实现混合编程。当前的环境是,win10,IDE是vs2019,python版本是3.9,…...
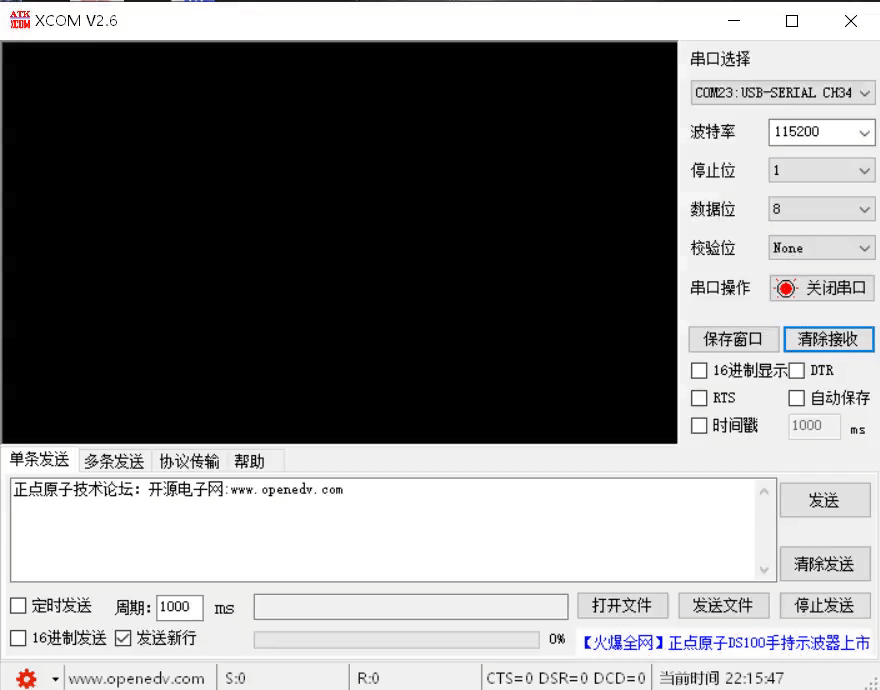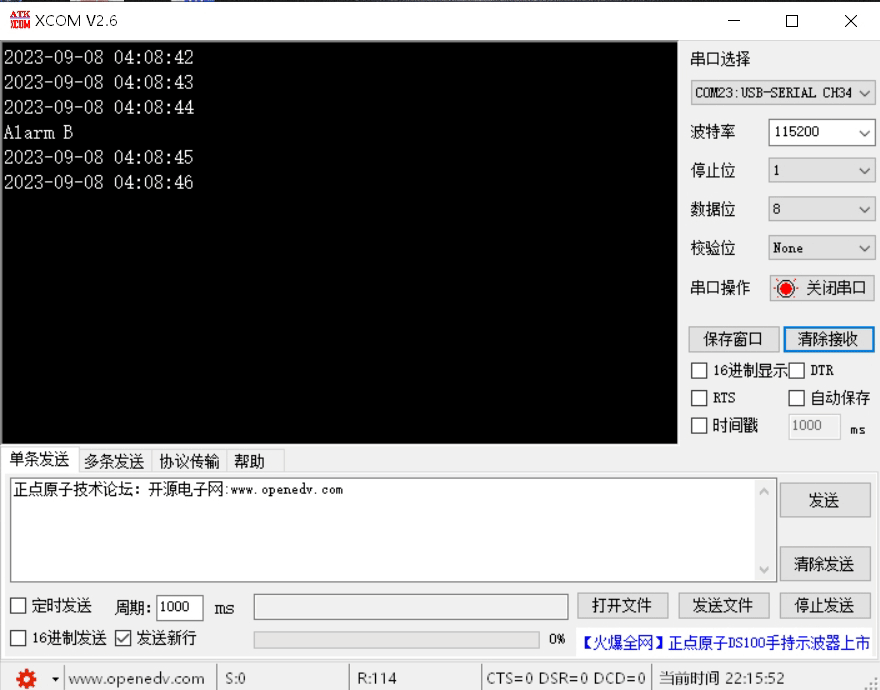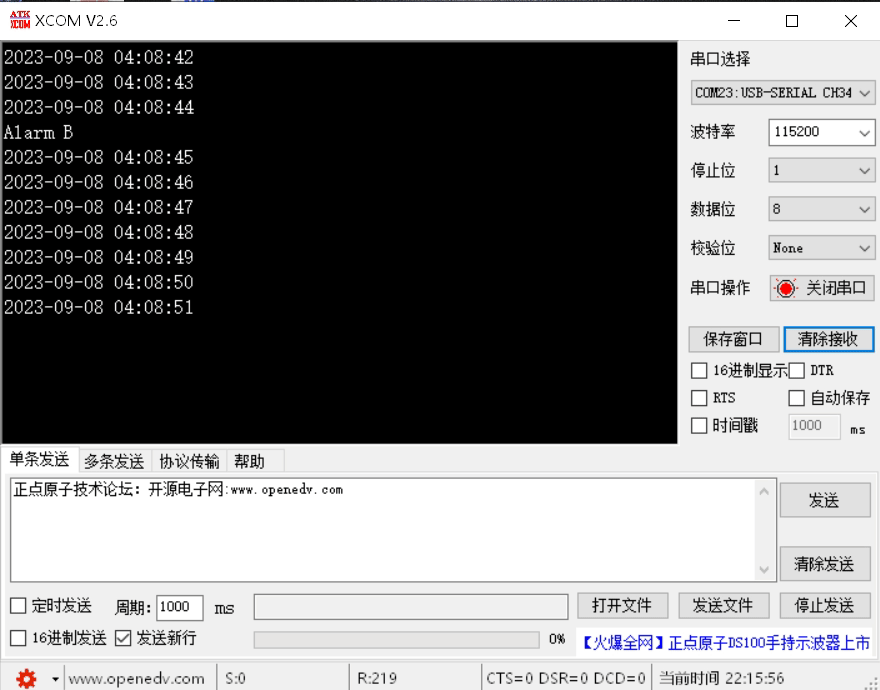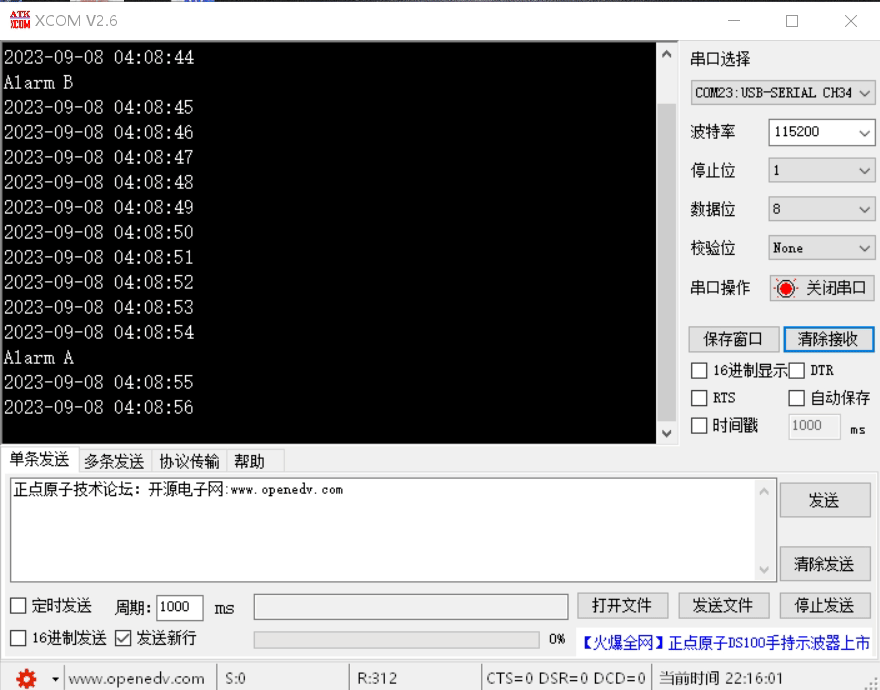
STM32F4X RTC
STM32F4X RTC 什么是RTCSTM32F4X RTCSTM32F4X RTC框图STM32F4X RTC计数频率STM32F4X RTC日历STM32F4X RTC闹钟 STM32F4X RTC例程 什么是RTC RTC全程叫Real-Time Clock实时时钟,是MCU中一个用来计时的模块。RTC的一个主要作用是用来显示实时时间,就像日常…...

[git] 如何克隆仓库,进行项目撰写,并绑定自己的远程仓库
摘要:删除.git文件,才可重新绑定远程仓库。 具体步骤: 文件夹右键,进入”Git Bash Here“执行命令 1. 执行 ”git clone 仓库地址“,克隆仓库 2. 在生成的仓库中,删除 .git 文件 3. git init 初始化仓库…...

【C++】模拟实现二叉搜索树的增删查改功能
个人主页:🍝在肯德基吃麻辣烫 我的gitee:C仓库 个人专栏:C专栏 文章目录 一、二叉搜索树的Insert操作(非递归)分析过程代码求解 二、二叉搜索树的Erase操作(非递归)分析过程代码求解…...

Yolov8-pose关键点检测:模型轻量化创新 | ScConv结合c2f | CVPR2023
💡💡💡本文解决什么问题:ScConv(空间和通道重建卷积),一个即插即用的架构单元,可以可以直接用来替代各种卷积神经网络中的标准卷积。 ScConv | GFLOPs从9.6降低至9,参数量从6482kb降低至6479kb Yolov8-Pose关键点检测专栏介绍:https://blog.csdn.net/m0_637742…...
)
【洛谷 P1060】[NOIP2006 普及组] 开心的金明 题解(动态规划+01背包)
[NOIP2006 普及组] 开心的金明 题目描述 金明今天很开心,家里购置的新房就要领钥匙了,新房里有一间他自己专用的很宽敞的房间。更让他高兴的是,妈妈昨天对他说:“你的房间需要购买哪些物品,怎么布置,你说…...
)
什么是CI/CD:持续集成与持续交付?(InsCode AI 创作助手)
在现代软件开发领域,CICD(Continuous Integration and Continuous Delivery)是一种关键性的开发实践,它有助于提高软件交付的质量和效率。本文将深入探讨CICD的定义、原理和重要性,以及如何在项目中实施CICD流程。 什…...

redis 高可用
Redis 高可用 在web服务器中,高可用是指服务器可以正常访问的时间,衡量的标准是在多长时间内可以提供正常服务(99.9%、99.99%、99.999%等等)。 但是在Redis语境中,高可用的含义似乎要宽泛一些,除了保证提供…...

什么样的词条可以创建维基百科?
维基百科在国内用得比较少,有一些特殊原因,维基百科的控制权海外,目前维基百科和谷歌是一样的,在国内是无法正常访问的。但做海外推广的朋友都是知道维基百科的,小马识途营销顾问认为它在世界互联网领域的地位…...

poll epoll初学习
正是select这些缺点,才有了poll 1.I/O多路转接之poll 2.I/O多路转接之epoll 其中的struct epoll_event:...
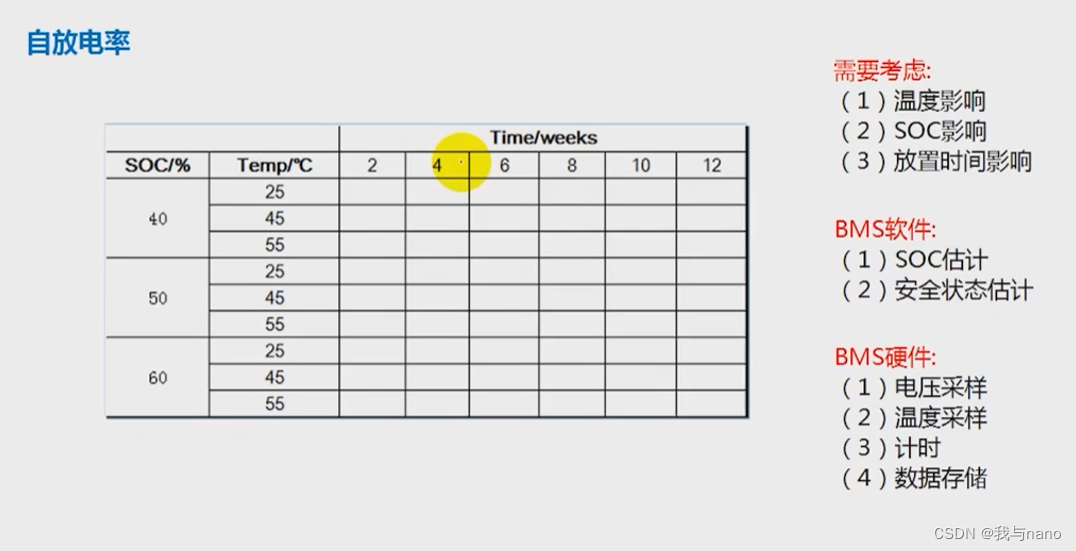
BMS电池管理系统——电芯需求数据(三)
BMS电池管理系统 文章目录 BMS电池管理系统前言一、有什么基础数据二、基础数据分析1.充放电的截至电压2.SOC-OCV关系表3.充放电电流限制表4.充放电容量特性5.自放电率 总结 前言 在新能源产业中电芯的开发也占有很大部分,下面我们就来看一下电芯的需求数据有哪些 …...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
